LSTM 오토인코더를 이용한 이상 탐지의 임계치 결정 방법

Ⅰ. 서 론

기기나 장비의 일반적인 유지, 보수 활동은 사전에 설정된 주기에 따라 점검하거나, 기기와 장비에 손상이나 고장이 발생했을 때 수리하는 것이다. 최근에는 기기나 장비에 고장이 발생하기 전에 미리 유지, 보수하는 예지 보전을 통해 기기나 장비의 무중단 서비스를 제공하고자 하는 연구들이 다양하게 진행되고 있다[1]. 특히, 예지 보전을 위해 인공지능 기술을 적용하는 연구도 있다[2].

본 논문은 쇼핑몰, 빌딩, 역사 등 유동 인구가 많은 건축물에 설치, 운영되고 있는 승강기의 예지 보전을 위해 요구되는 운행상태의 이상 감지를 위해 LSTM Autoencoder(이하 AE)를 사용할 때 정상과 이상을 판별하는 기준인 임계치를 설정하는 방법을 제안한다. 기기의 이상 탐지를 위한 방법 중 LSTM AE를 이용한 연구는 LSTM AE 기계학습 모델을 이용하여 기기에서 검출된 센서 데이터의 이상 여부를 결정하였다[3]. LSTM AE 모델의 출력을 이용한 이상 여부 결정은 사전에 설정된 기준값 즉, 임계치(Threshold)가 필요하다. 하지만, 기존 연구에서는 임계치를 결정하는 방법을 제시하지 않았다. 본 논문에서는 LSTM AE 기계학습 모델의 출력을 정상, 이상으로 판단하는 기준값인 임계치를 결정하는 방법을 제안한다.

이상 탐지(Anomaly detection)는 기기의 동작 상태 데이터에 있는 이상 패턴을 찾는 것이다. 기기의 동작 상태 데이터는 일정한 시간 간격에 따라 주기적으로 수집된 시계열 데이터이다. 시계열 데이터 분석을 통한 이상 감지는 기기 고장의 전조 현상으로 인한 동작 상태 데이터 패턴의 불일치를 감지하는 것으로, 고장 발생 전 사전 점검 활동인 예지 보전을 가능하게 한다[4]. 시계열 데이터 분석을 통한 이상 탐지와 관련된 최근의 많은 연구는 이상 패턴 검출을 위해 기계학습을 사용하고 있다[5]-[7]. 기계학습은 정답이 존재하는 지도학습과 정답이 존재하지 않은 비지도 학습으로 나눌 수 있다. 승강기 등의 기기 고장은 빈번하지 않으므로 본 논문에서는 정상 패턴의 특징 학습에 비지도 학습 모델 중 LSTM AE를 이용하였다. 학습된 LSTM AE 모델의 출력은 정상 패턴의 데이터와 이상 패턴의 데이터에 대해 각각 다르므로, 정상과 이상을 판별하는 기준값인 임계치를 이상 탐지에 사용한다[8][9]. 본 논문에서는 비지도 학습 모델 중 하나인 LSTM AE를 이용하여 이상 탐지를 할 때 정상과 이상을 구분하는 기준값인 임계치를 결정하는 방법을 제안하고, 케글에 공개된 펌프 데이터를 이용하여 본 논문의 임계치 결정 방법이 효과적임을 보였다.

Ⅱ. 기존 연구

Ⅲ. 임계치 결정 방법

LSTM AE는 모델에 입력된 시계열 데이터를 인코드하여 1차원의 잠재 벡터(latent vector)를 생성하고, 이를 다시 디코드하여 입력된 데이터를 복원하여 출력한다. 이 모델은 학습 데이터와 유사한 입력 데이터에 대한 복원된 데이터 간의 차이인 복원 오차의 크기가 크지 않다는 특징이 있다. 반면, 학습 데이터와 차이가 있는 입력 데이터에 대한 복원 오차의 크기는 상대적으로 크다.

LSTM AE의 이러한 특징은 이 모델을 이용한 이상 탐지에서 입력 데이터의 정상 또는 이상을 결정할 때 기준이 되는 임계치가 정상 데이터의 복원 오류의 크기보다 크고, 이상 데이터의 복원 오류의 크기보다 작음을 의미한다. 따라서, LSTM AE를 이용한 이상 탐지에서 임계치의 결정이 이상 탐지 성능을 결정하는 주요 요소 중의 하나이다.

정상 또는 이상 데이터에 대한 복원 오차의 크기에 관한 LSTM AE의 특성을 고려하여 본 논문에서 제안하는 임계치 결정 방법은 정상 데이터를 이용하여 학습한 LSTM AE가 임계치 결정 데이터 세트 중 정상 데이터를 대상으로 한 복원 오차와 이상 데이터를 대상으로 한 복원 오차의 크기를 이용하는 것이다.

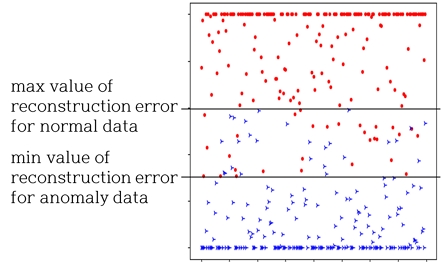
그림 1은 LSTM AE 모델에 정상과 이상 데이터를 입력했을 때 생성된 복원 데이터에 대한 복원 오차 크기를 나타낸 것이다. 그림 1에서 정상과 이상 데이터에 대한 복원 오차의 크기는 각각 기호 와 ∙로 표시하였으며, 이것은 실제 데이터를 이용한 복원 오차가 아니며, 임계치 결정 방법을 기술하기 위해 생성된 것이다.

Fig. 1.

Max and min value of reconstruction error

앞서 기술한 바와 같이 정상 데이터를 학습한 LSTM AE는 정상 데이터 입력에 대한 복원 오차의 크기가 상대적으로 적은 데이터를 출력한다. 반면, 이상 데이터 입력에 대해 LSTM AE는 상대적으로 복원 오차가 큰 데이터를 출력한다. 따라서, 이상 데이터에 대한 복원 오차의 크기는 정상 데이터의 그것보다 크므로 기호 ∙가 그림의 상단에 있으며, 기호 가 그림의 하단에 있다. 하지만, 정상 데이터를 위한 복원 오차 크기의 최댓값과 이상 데이터를 위한 복원 오차 크기의 최솟값 사이의 범위에 포함되는 복원 오차를 갖는 데이터는 그림 1에 표시한 것과 같이 정상 또는 이상 데이터일 수 있다. 따라서, 이 두 값의 범위 내 값을 임계치를 설정하여야 한다.

설정된 임계치에 따라 복원 오차의 크기가 이 범위 내에 있는 데이터는 거짓 양성(False positive)과 거짓 음성(False negative)이 될 수 있다. 예를 들어, 설정된 임계치보다 큰 복원 오차 크기를 갖는 정상 데이터는 이상으로 결정되어 거짓 양성의 결과가 된다. 따라서, 설정된 임계치는 모델의 이상 탐지 성능에 영향을 준다.

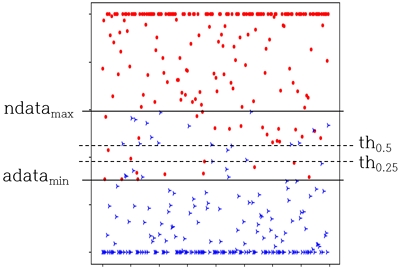
본 논문에서 제안하는 임계치 th_α 설정 방법은 정상 데이터에 대한 복원 오차 크기의 최댓값 ndata_max, 이상 데이터에 대한 복원 오차 크기의 최솟값 adata_min, 분할 비율 α를 적용한 식 (1)을 이용한다. 분할 비율 α는 범위 (adata_min, ndata_max)를 임계치로 분할 할 비율을 의미하며, 0과 1 사이의 실수이다.

그림 2는 그림 1에 나타낸 복원 오차 그래프에서 분할 비율 α가 0.5, 0.25일 때 분할된 범위를 나타낸 것이다. 이 예는 분할 비율이 0.5일 때 보다 0.25일 때 이상 데이터를 더 많이 감지하지만, 상대적으로 더 많은 정상 데이터를 이상 데이터로 결정한다. 이 경우에 거짓 음성은 감소하지만, 거짓 양성은 증가한다. 즉, 분할 비율이 LSTM AE의 이상 감지 성능에 영향을 줄 수 있다.

Fig. 2.

Threshold value according to α

분할 비율의 결정은 학습된 LSTM AE 모델의 시험 단계에서 학습 데이터에 포함되지 않은 정상 데이터와 이상 데이터의 복원 오차를 대상으로 분할 비율의 변화에 따른 정확도, 재현율 등을 도출하고, 이 지표들이 응용 분야의 목적에 적합한 값이 될 때의 비율로 한다. 예를 들어, 승강기 등 고장 발생으로 인한 비용이 큰 응용은 거짓 양성이 증가하지만, 거짓 음성을 감소시킬 수 있는 분할 비율이 고장 발생으로 인한 직, 간접적 비용과 거짓 양성으로 인한 추가 점검 비용 간의 균형이 되도록 설정한다.

Ⅳ. 구현 및 실험 결과 분석

4.1 구현 환경

LSTM AE를 사용한 시계열 데이터의 이상 탐지를 위해 본 논문에서 제안한 임계치 결정 방법이 유효함을 보이기 위해 케글(Kaggle)에 공개된 펌프 데이터[13]를 위한 LSTM AE 모델을 구현하고, 임계치를 결정하여 이상 탐지실험을 하였다. 본 논문에서 이용한 펌프 데이터는 2018년 4월에서 2018년 8월까지 소규모 지역에서 운영된 펌프들의 동작 상태를 분 단위로 검출한 52개의 센서 데이터와 검출 시간 정보로 구성된 약 22만 행의 데이터이다. 실험에 사용한 데이터는 손실 데이터가 많은 두 개의 센서 데이터를 제거한 50개 데이터를 표준화한 것이며, 각 데이터에 정상 또는 이상을 구분할 수 있는 레이블이 포함되어 있다.

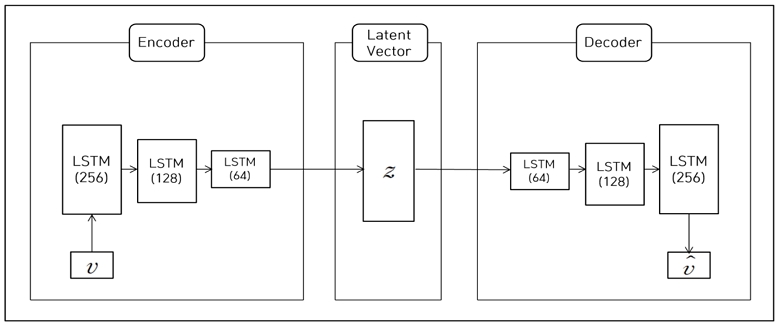
그림 3은 펌프 데이터를 대상으로 한 이상 탐지를 위해 본 논문에서 구현한 LSTM AE 모델을 나타낸 것이다. LSTM AE 모델을 구성하고 있는 인코더와 디코더는 각각 세 개의 LSTM 신경망 계층으로 구성되어 있다. 인코더는 시계열 데이터 입력을 인코드하여 크기가 20인 잠재 벡터를 생성하며, 디코더는 이 잠재 벡터를 입력으로 하여 인코더의 입력 데이터와 같은 차원과 크기를 갖는 데이터를 복원한다.

Fig. 3.

LSTM AE architecture

4.2 데이터 전처리와 학습

구현한 LSTM AE 모델의 학습 및 시험을 위해 본 연구에서는 22만여 개의 50개 센서 데이터 세트를 이용하여 시계열 데이터 세트를 생성하였다. 모델의 학습이 정상 데이터를 대상으로 하므로 시계열 데이터 생성은 데이터 세트를 정상 데이터와 이상 데이터로 나눈 후 진행하였다. 시계열 데이터 세트 생성을 위해 각 시계열 데이터는 검출 시간이 연속된 열여섯 개의 센서 데이터로 구성하였다. 예를 들어, 검출 시간이 n인 50개 센서 데이터를 s_n이라고 할 때, 생성한 시계열 데이터는 (s₀ ⋯ s₁₅), (s₁ ⋯ s₁₆) 등과 같이 검출 시간이 연속된 센서 데이터로 구성하였다. 이러한 방법으로 정상 데이터와 이상 데이터를 이용하여 생성한 시계열 데이터의 개수는 각각 205,686개와 14,363개이며, 각 시계열 데이터의 크기는 (205686, 16, 50)과 (14363, 16, 50)이다. 본 연구에서는 정상 시계열 데이터를 모델 학습용, 임계치 결정용, 시험용으로 각각 0.8, 0.1, 0.1의 비율로 분할 하였으며, 이상 시계열 데이터도 임계치 결정용, 시험용으로 각각 0.5, 0.5의 비율로 분할 하였다.

본 논문에서 구현한 LSTM AE 모델의 논리적 동작은 크기가 (16, 50)인 한 개의 시계열 데이터 입력에 대해 입력과 같은 크기의 복원된 데이터를 출력한다. 복원 오차는 입력과 출력 데이터 간의 차이를 나타내는 것으로 모델이 입력 데이터에 대해 완벽하게 복원된 데이터를 출력한다면 0이 된다. 본 논문에서 사용한 복원 오차는 입력과 출력 데이터 간 평균 제곱 오차(MSE, Mean Squared Error)이며, 입력 데이터의 정상 또는 이상으로 판단하는 지표가 된다. 표 1은 본 논문에서 실시한 실험 환경과 인자를 나타낸 것이다.

Table 1.

Experimental environment and parameters

4.3 임계치 결정

임계치 결정은 앞에서 기술한 것과 같이 학습용 데이터를 이용한 학습이 완료된 모이 임계치 결정용 데이터 입력과 복원된 출력의 복원 오차를 이용하였다. 본 논문의 실험에서 사용한 정상 데이터의 최대 복원 오차 ndata_max와 이상 데이터의 최소 복원 오차 adata_min는 각각 15.0313(소수점의 네 번째 자리에서 버림), 3.5025이다. 펌프 동작 상태의 이상 검출을 위해 모델이 탐지한 거짓 음성과 거짓 양성 간의 균형을 고려한 이상 탐지 성능을 위해 본 논문의 실험은 분할 비율 α의 값을 0.5, 0.25, 0.125, 0.0635로 할 때 임계치를 각각 설정하고, 이에 따른 이상 탐지 성능을 분석하였다. 또, 제안한 임계치 결정 방법에 따른 이상 탐지 성능을 비교하기 위해 본 논문에서는 정상 데이터의 평균값과 이상 데이터의 평균값의 중간값을 임계치로 설정한 것과 정밀도-재현율 그래프[11]를 이용하여 임계치를 설정한 것을 함께 분석하였다.

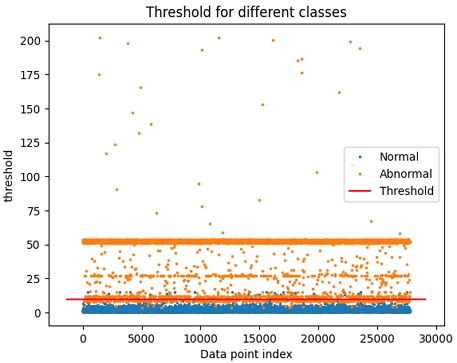
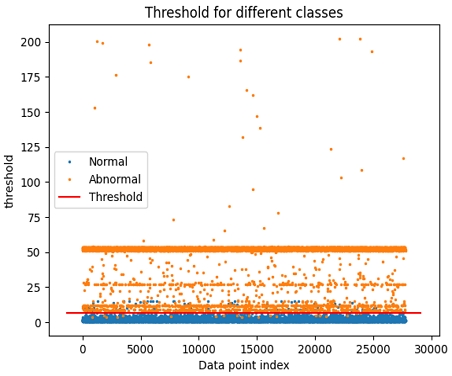
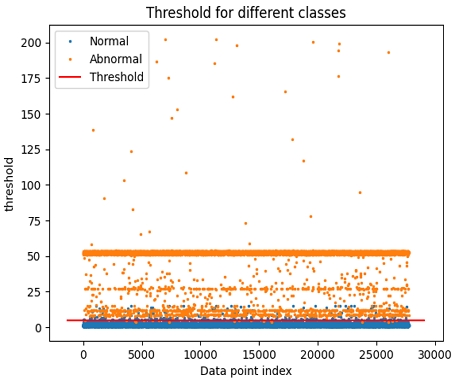
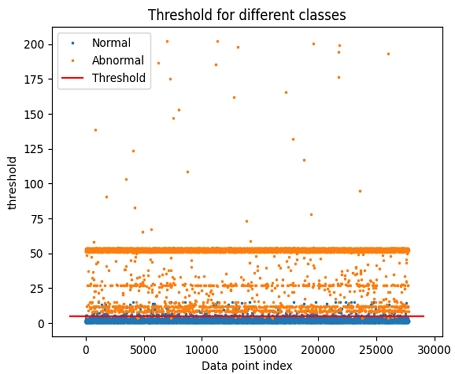
그림 4부터 7까지는 본 논문에서 제안한 방법에 따라 α값이 각각 0.5, 0.25, 0.1125, 0.0625일 때 결정한 임계치를 기준으로 정상, 이상 데이터를 분류한 것이다. 그림의 붉은 선은 α값에 따라 결정된 임계치를 나타낸 것이며, 이 선의 위쪽에 표시된 데이터는 임계치보다 큰 복원 오차를 갖는 것으로 이상 데이터로 분류된다. 또, 임계치 선의 아래쪽에 표시된 데이터는 임계치보다 작은 복원 오차 크기를 갖는 것으로, 정상 데이터로 분류된다.

Fig. 4.

Normal and abnormal data at α=0.5

Fig. 5.

Normal and abnormal data at α=0.25

Fig. 6.

Normal and abnormal data at α=0.125

Fig. 7.

Normal and abnormal data at α=0.0625

임계치보다 더 큰 복원 오차 크기로 인해 이상 데이터로 분류되는 정상 데이터 즉, 임계치 선보다 위쪽에 표시된 정상 데이터는 거짓 양성이다. 또, 임계치보다 작은 복원 오차로 인해 정상 데이터로 분류되는 이상 데이터는 임계치 선 아래쪽에 있으며, 이 데이터는 거짓 음성이다.

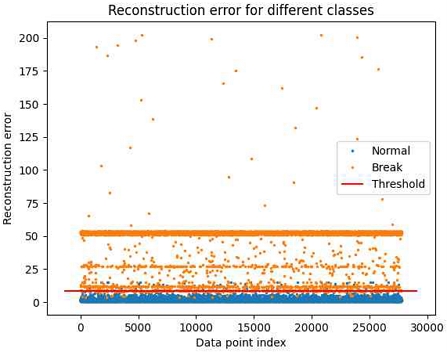
그림 8은 LSTM AE 모델이 정상 데이터의 복원 오차의 평균과 이상 데이터의 복원 오차의 평균 사이의 중간값을 임계치로 설정한 경우를 나타내고 있으며, 그림 9는 정밀도-재현율 그래프의 교차점을 임계치로 설정한 경우를 나타내고 있다.

Fig. 8.

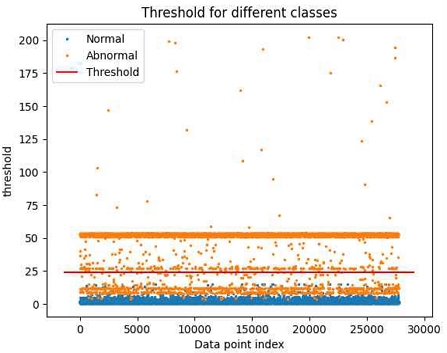
Normal and abnormal data when the median value between reconstruction error averages of normal and abnormal data is a threshold

Fig. 9.

Normal and abnormal data when the cross-point value of the precision-recall graph is a threshold

표 2는 임계치 결정용 데이터 세트를 이용하여 실험한 결과를 나타낸 것이다. 거짓 음성은 이상 데이터를 정상 데이터로 잘못 결정한 것이며, 장치 또는 설비에 있는 이상 조짐의 선제적 탐지 실패로 인한 서비스 중단 등의 비용이 증가할 수 있다. 반면 거짓 양성은 정상 데이터를 이상 데이터로 잘못 결정한 것이며, 설비에 대한 추가적인 점검 비용이 필요하다. 도시를 위한 펌프, 승강기 등 고장 발생으로 인한 직간접적 비용이 큰 영역에서는 거짓 음성을 감소시킬 수 있도록 임계치가 설정되어야 한다. 하지만, 거짓 음성 감소를 위해 낮은 임계치를 사용하면 거짓 양성이 증가한다. 따라서, 거짓 음성의 감소와 거짓 양성의 증가 사이에 균형(Tradeoff)이 되는 임계치의 결정이 필요하다. 이를 위해 본 논문에서는 정확도와 재현율(TPR, True Positive Rate)를 고려하여 임계치를 결정하였다. 표 2는 본 논문에서 제안한 임계치 결정 방법의 α값이 0.25, 0.125, 0.0625일 때 다른 실험보다 높은 재현율을 보였고, 이들 중 α값이 0.25일 때 정확도가 가장 높다는 것을 보였다. 따라서, 본 논문에서는 임계치 결정용 데이터를 이용하여 결정한 6.385를 실험용 데이터를 대상으로 한 이상 탐지를 위한 임계치로 설정하여 성능을 평가하였다.

Table 2.

Experimental results of data for deciding threshold

4.4 모델 성능 평가

본 논문에서 제안한 임계치 결정 방법의 유효함을 보이기 위한 실험은 앞서 결정한 값 6.385를 임계치로 설정하여 시험용 데이터 세트를 이용하여 실시하였다. 표 3은 결정한 임계치, 평균의 중간값, 정밀도-재현율 그래프를 이용한 이상 탐지 성능을 나타낸 것이다.

Table 3.

Experimental results of test data

표 3은 본 논문에서 제안한 방법으로 결정한 임계치를 이용하는 것이 정상 데이터와 이상 데이터의 복원 오차 평균값의 중앙값을 임계치로 설정하거나 정밀도-재현율 그래프의 교차점을 임계치로 설정하는 것보다 더 높은 정확도와 재현율을 보였다. 따라서, 이 실험 결과는 본 논문에서 제안한 임계치 결정 방법이 LSTM AE를 이용한 시계열 데이터 분석을 통한 기기 이상 탐지 성능 향상에 긍정적 효과가 있음을 보였다.

Ⅴ. 결 론

본 논문은 기기의 동작 상태를 감시하는 센서 데이터를 분석하여 기기 동작의 정상 또는 이상을 시계열 데이터 기반으로 탐지하는 LSTM AE 모델에서 임계치를 결정하는 방법을 제안하였다. 본 논문에서 제안한 방법은 학습이 완료된 LSTM AE 모델에 임계치 결정용 데이터 중 정상 데이터의 최대 복원 오차와 이상 데이터의 최소 복원 오차 사이의 비율을 이용하여 임계치를 설정하는 것이다. 본 논문에서 제안한 임계치 결정 방법이 LSTM AE 모델을 이용한 이상 탐지 성능 향상에 효과가 있음을 보이기 위해 케글에 공개된 펌프 데이터를 이용하여 실험하였다. 실험 결과는 기기의 이상 조짐을 사전에 파악하여 대응하는 예지 보전이 요구되는 응용 분야에 본 논문에서 제안한 임계치 결정 방법이 이상 탐지 성능 향상에 기여함을 보였다.

향후 연구과제는 에스컬레이터 등에 설치된 인버터, 각종 센서 등이 검출한 승강기 운행상태 데이터 분석을 위한 기계학습 모델의 고도화 및 시험 운행 데이터를 기반으로 한 임계치 자동 결정 방법 등이 있다.

Acknowledgments

본 연구는 정부(과학기술정보통신부)의 ICT R&D 혁신 바우처 사업의 지원을 받아 수행된 연구임(No. 2022-0-0084530382068210001)

References

• J. H. Park, E. K. Oh, M. K. Jang, Y. W. Seo, and S. W. Hu, "Improved Forecasting Algorithm for Vessel Engine Failure", Journal of KIIT. Vol. 15, No. 11, pp. 175-185, Nov. 2017. [https://doi.org/10.14801/jkiit.2017.15.11.175]
• T. S. Ki and S. H. Lee, "A Prediction Scheme for Power Apparatus using Artificial Neural Networks", Journal of Convergence Information, Vol. 7, No. 6, pp. 201-207, Dec. 2017. [https://doi.org/10.22156/CS4SMB.2017.7.6.201]
• S. H. Jeon, C. L. Park, G. W. Lee, S. J. Kim, and B. G. Gu, "LSTM Autoencoder Implementation for Anomaly Detection of Equipment", Fall Conference of KIIT, Jeju, Dec. 2022.
• J. H. Lee, S. Y. Yoo, S. C. Shin, D. H. Kang, S. S. Lee, and J. C. Lee, "Fault diagnosis of bearings using machine learning algorithm", Journal of the Korean Society of Marine Engineering, Vol. 43, No. 6 pp. 455-462, 2019. [https://doi.org/10.5916/jkosme.2019.43.6.455]
• V. Q. Nguyen, L. V. Ma, and J. S. Kim, "LSTM-based Anomaly Detection on Big Data for Smart Factory Monitoring", Journal of Digital Contents Society, Vol. 19, No. 4, pp. 789-799, Apr. 2018. [https://doi.org/10.9728/dcs.2018.19.4.789]
• S. H. Lee, S. K. Ko, and S. A. Lee, "Fault Classification Model Based on Deep Learning Using Vibration Data of Mechanical Equipment", Journal of Korean Institute of Next Generation Computing, Vol. 18 No. 2 pp. 36-46, Apr. 2022. [https://doi.org/10.23019/kingpc.18.2.202204.004]
• J. S. Choi, "Predictive Maintenance of the Robot Trouble Using the Machine Learning Method", Journal of the Semiconductor & Display Technology, Vol. 19, No. 1, Mar. 2020.
• M. S. Elsayed, N. Le-Khac, S. Dev, and A. D. Jurcut, "Network Anomaly Detection Using LSTM Based Autoencoder", Q2SWinet '20, Alicante, Spain, pp. 37-45, Nov. 2020. [https://doi.org/10.1145/3416013.3426457]
• H. D. Nguyen, K. P. Tran, S. Thomassey, and M. Hamad, "Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in Supply Chain Management", International Journal of Information Management, Vol. 57, Apr. 2021. [https://doi.org/10.1016/j.ijinfomgt.2020.102282]
• S. J. Kim and T. S. Shon, "LSTM Autoencoder-Based Insider Data Leak Detection", Journal of Digital Contents Society Vol. 23, No. 6, pp. 1159-1166, Jun. 2022. [https://doi.org/10.9728/dcs.2022.23.6.1159]
• J. H. Lee and J. M. Sohn, "Escalator Anomaly Detection Using LSTM Autoencoder", 2021 Summer Conference of Korea Society of Computer Information, Vol. 29, No. 2, pp. 7-10, Jul. 2021.
• J. G. Lee and D. H. Kim, "Case Study on Fault Diagnosis of Radiator Using LSTM Autoencoder", The Journal of KINGComputing, Vol. 16, No. 6, pp. 17-25, Dec. 2020.
• pump_sensor_data, https://www.kaggle.com/datasets/nphantawee/pump-sensor-data, , [accessed: Oct. 05, 2022]