타 단말 신호를 이용하는 K-means 기반 채널 추정 기법

Ⅰ. 서 론

이동 통신 시스템에서, 다중경로채널(Multipath channel)을 추정하기 위하여 기지국(Base Station, BS)과 사용자 단말(User Equipment, UE)은 자원블록(Resource block)에 데이터 신호와 파일럿 신호(Pilot signal)를 동시에 전송한다[1]. 수신기는 파일럿 신호를 이용하여, 채널에 의하여 왜곡된 데이터 신호의 크기(Amplitude)와 위상(Phase)을 보상한 후 복조함으로써 데이터를 복호할 수 있다. 그러나 한정된 무선자원에 데이터와 파일럿 신호를 전송하는 이동 통신 시스템에서 파일럿 신호는 정보를 포함하지 않고 있으므로, 파일럿 신호의 전송에 사용되는 시간과 주파수 자원이 증가할수록 이동통신 시스템의 실질적인 데이터 전송률을 감소할 수밖에 없다. 파일럿 신호를 전송함으로써 발생하는 데이터 전송률 감소 문제를 해결하기 위하여 채널 추정 성능을 일정 수준으로 유지하면서 파일럿 신호가 사용하는 무선자원의 양을 감소시키는 연구가 있어왔다[2]-[4].

파일럿 신호에 대한 오버헤드를 감소시키기 위하여 순환(Cyclic) 코드를 사용한 연구에서, 순환 코드의 패턴에 따라 파일럿 신호가 형성되고 채널 추정 성능을 기존의 최소 제곱(Least-Squares, LS) 채널 추정기 및 최소 평균 제곱 오차(MMSE, Minimum Mean Squared Error) 채널 추정기와 비교하였다[2]. 복수의 안테나를 위한 파일럿 신호 설계에 있어, 파일럿 신호의 양은 안테나 수에 비례하기 때문에 동일한 자원에 파일럿 신호를 중첩함으로써 채널 추정 오차는 최소화하면서 파일럿 신호를 위한 무선 자원 오버헤드를 감소시켰다[3]. 또한, 파일럿 전송을 위한 무선 자원 오버헤드의 감소에 따른 채널 추정 성능의 변화가 무선 통신 시스템 용량에 미치는 영향을 분석하였다[4]. 이와 같이 기존의 연구에서는 파일럿 신호는 사용하되, 파일럿 신호의 파형(Waveform)과 자원 할당 방식에 변화를 주어 파일럿 신호 전송을 위한 오버헤드를 감소시켰다.

한편, 파일럿 신호 전송 오버헤드를 감소시키기 위해 파일럿 신호를 전송하지 않고, 데이터 심볼들의 크기와 위상 변화만으로 채널을 추정하는 연구들이 진행되었다[5]-[8]. 이들 연구에서는 K-means 군집화 알고리즘을 활용하여[9] 수신된 복수의 데이터 심볼들을 4 개의 군집으로 분리하고, 각 군집의 중심점의 크기와 위상 값을 이용하여 채널을 추정하고 있다. 파일럿 신호를 사용하지 않기 때문에 파일럿 신호 없는 채널 추정기(Pilotless Channel Estimator, PCE)로 명명되었다. PCE는 K-means 군집화 연산 과정에서 잡음 억제 효과를 얻게 되어, 수신된 심볼의 수가 일정 개수 이상일 때 기존의 채널 추정기 대비 우수한 채널 추정 성능을 보여주었다[5][6]. PCE은 데이터 심볼들이 16QAM 이상의 고차 변조인 경우에도 적용이 가능하여, 데이터 심볼이 QPSK 내지 256QAM으로 변조되어 전송되는 경우에 대한 채널 추정기가 제안되고 성능이 평가되었다[7][8].

이러한 PCE들에 대한 연구들을 통하여 PCE의 채널 추정 성능이 기존 채널 추정기들 대비 우수하다는 것은 검증이 되었으나, PCE를 16QAM 이상의 고차 변조된 데이터 심볼들에 적용함에 있어 문제점이 발견되었다[8]. PCE는 성상도(Constellation)의 모든 심볼 위치에 데이터 심볼들이 고르게 분포되어야만 정상적으로 군집화가 진행되어 채널을 추정할 수 있다[8]. 따라서 변조 차수(Order)가 증가할수록 성상도 상의 심볼의 수가 비례하여 증가하므로, PCE에 필요한 데이터 심볼의 수는 증가하게 된다. 예를 들면 QPSK의 경우 성상도에서 심볼의 위치가 4 개에 불과하므로 이상적인 경우 4개 이상의 데이터 심볼만으로 군집화가 가능하다. 그러나 256QAM의 경우 성상도 상의 심볼 위치만 256개이기 때문에 최소 256개 또는 그 이상의 데이터 심볼이 수신되어야 PCE를 동작시킬 수 있다. 따라서 특정 UE가 256QAM을 수신할 수 있는 무선 환경에 있더라도 해당 UE에 전송할 데이터 심볼의 수가 충분하지 않다면 PCE를 이용한 채널 추정을 할 수 없다는 문제점이 있다.

현재 운용되고 있는 4세대(4G) 및 5세대(5G) 이동 통신 시스템은 슬롯단위로 무선 자원을 할당한다[10][11]. 하나의 UE에 할당된 무선 자원에는 채널 품질 지시자(Channel quality indicator)에 기반하여 결정된 변조기법이 적용된 데이터 심볼이 전송된다[10]. 하향링크(Downlink)로 전송된 UE들의 데이터는 4G와 5G 이동통신 시스템에서 각각 EPS-AKA(4G에서 사용되는 Evolved Packet System - Authentication and Key Agreement), 5G-AKA 등의 절차에 따라 암호화되어 있기 때문에 다른 UE가 복호할 수 없다. 그러나 AKA와 상관 없이 무선으로 전송되는 데이터 심볼에는 사전에 CQI 표에 정의된 변조 기법만을 사용하기 때문에, 하향링크에서 한 UE는 모든 UE들의 변조된 단계의 데이터 심볼을 모두 수신할 수 있다.

본 논문에서는 하향링크에서 다른 UE들의 데이터 심볼을 이용하여 채널 추정 성능을 개선할 수 있는 PCE를 제안한다. 위에서 언급한 바와 같이 고차 변조된 데이터 심볼의 경우 PCE의 성능은 수신된 심볼 수가 증가함에 따라 개선된다[8]. 따라서 동일한 주파수의 시간적으로 인접한 슬롯에서 전송되는 다른 UE들의 데이터 심볼들을 PCE에 활용함으로써 실질적으로 수신된 심볼 수가 증가하는 효과를 얻고, 이로부터 PCE의 성능을 개선할 수 있다. 기지국은 암시적(Implicit: 3GPP 이동통신 표준에서 명시적 제어 명령이 아닌 모드 또는 다른 제어 파라미터 등에 의해 간접적으로 전달되는 명령) 자원할당 규칙에 의해서 동일한 기법으로 변조된 서로 다른 UE들의 데이터 심볼을 동일한 주파수 대역에 순차적으로 전송함으로써 PCE를 동작시키는 UE가 수신 심볼 수가 부족할 때 다른 UE의 데이터 심볼을 사용할 수 있도록 한다. 또는 UE들 간 서로 다른 변조 기법을 사용하는 경우에도 순차적 K-means 군집화(Sequential K-means Clustering, SKC) 기법을 활용하여 채널 추정 성능을 개선할 수 있도록 PCE를 제안하였다. 본 논문에서 제안하는 PCE 기법의 성능은 평균 제곱 오차(MSE, Mean Square Error)와 심볼 오류율(SER, Symbol Error Rate)에 의하여 평가되었다. 이러한 성능 개선은 추가적인 연구를 통하여 MIMO 채널 추정 연구에 활용될 수 있다[12].

II장에서는 시스템 모델이 정의된다. III장에서는 하나의 UE가 다른 UE의 데이터 심볼을 활용하여 PCE를 수행하는 과정을 설명한다. IV장에서는 다른 UE의 심볼을 활용하여 동작하는 PCE의 성능이 평가되며, V장에서 연구 결과 요약 및 결론이 제시된다.

Ⅱ. 시스템 모델

직교 주파수 분할 다중 접속(Orthogonal Frequency Division Multiple Access, OFDMA) 기반의 이동통신시스템은 복수의 직교 주파수 분할 다중화(Orthogonal Frequency Division Multiplexing, OFDM) 심볼과 부반송파(Subcarrier)로 구성되어 UE에게 무선 자원을 스케쥴링(Scheduling)할 수 있는 무선 자원 단위를 가지고 있으며 슬롯이라고 한다. 4G와 5G 시스템에서 하나의 슬롯은 주파수 영역에서 12개의 부반송파(Subcarrier)와 시간영역에서 하나의 슬롯에 해당되는 OFDM 심볼 수로 구성된다[10][11]. 하나의 슬롯에 포함되는 부반송파의 수 및 하나의 서브프레임(Subframe)을 구성하는 슬롯의 수는 시스템마다 다를 수 있지만, 하나의 UE에게 스케쥴링할 수 있는 최소 단위가 슬롯임은 4G와 5G 시스템에서 동일하다.

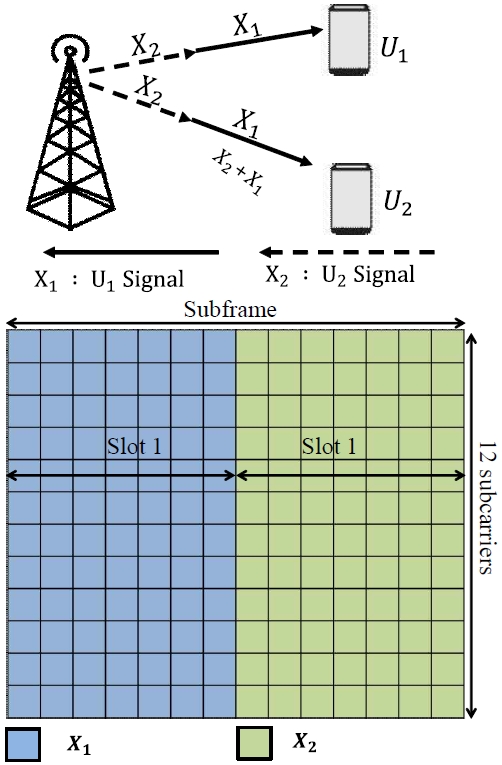
그림 1에는 시스템 모델이 도시되어 있다. 두 개의 UE U₁과 U₂가 있으며, 두 UE에게 전달되는 데이터 심볼의 집합을 각각 X₁, X₂로 표기한다. 하향링크에서 X₁과 X₂는 동일한 주파수에서 시간적으로 연속된 슬롯에 스케쥴링되어 전송된다. 인접한 두 개의 슬롯 시간동안 채널은 일관성(Coherence)을 유지한다고 가정한다. 그림 1의 서브프레임은 X₁과 X₂가 실제로 어떤 슬롯에 할당되어 전송되는지 보여주고 있다. 주파수 영역에서 하나의 슬롯은 12개의 부반송파만큼의 주파수를 점유하고 있음을 확인할 수 있으며, 그림 1에서는 7개의 OFDM 심볼이 하나의 슬롯을 형성하여 하나의 UE에 할당되는 자원블럭의 크기는 부반송파 12개와 OFDM 심볼 7개로 구성되어 있음을 확인할 수 있다. 5G의 경우 가변적 부반송파 간격(Subcarrier spacing)을 사용하므로 하나의 서브프레임은 두 개 이상의 슬롯들로 구성될 수 있다[10].

Fig. 1.

System model and subframe structure

Ⅲ. 타 단말의 신호를 이용한 채널 추정

3.1 타 단말의 신호를 고려한 수신 신호

그림 1의 U₁과 U₂는 서로 다른 두 개의 UE들을 의미하며, X₁과 X₂는 U₁과 U₂의 데이터 심볼들에 대한 벡터이다. 설명의 편의상 U₁에서 PCE가 동작한다고 가정한다. 이 때 PCE 입력에 주어지는 U₁의 수신 신호는 다음과 같이 표현될 수 있다.

$\[ y=hX+n \]$

(1)

(1)에서 X = [X₁,X₂],X∈C^{1×(N₁×N₂)}이다. N₁과 N₂는 각각 X₁과 X₂에 속하는 심볼의 수를 의미하며, X는 X₁과 X₂를 행 방향으로 연접(Concatenation)한 벡터이다. 식 (1)에서 X₁과 X₂는 U₁과 U₂의 CQI(Channel Quality Indicator) 레벨에 따라 QSPK, 16QAM, 64QAM, 256QAM 중 하나를 선택하여 전송할 수 있으며, 서로 다른 변조기법을 사용할 수 있다. h는 레일리(Rayleigh) 채널로써 복소 가우시안(Complex-Gaussian) 확률 분포를 따른다. n은 백색잡음(Additive white Gaussian noise)으로써 평균값이 0이고 표준편차가 N₀인 복소 가우시안 확률 분포를 따르는 랜덤 변수이다[13].

U₁과 U₂가 같은 변조기법을 사용하는 경우는 기존의 K-means를 사용하는 채널추정기법에서 수신 데이터 심볼의 수가 증가한 것과 동일하기 때문에[6][8], 본 논문에서 U₁와 U₂는 서로 다른 변조기법만 사용한다고 가정한다. 예를 들면 X₁이 QPSK 신호일 경우, X₂는 16QAM, 64QAM, 256QAM 신호 중에 하나이다.

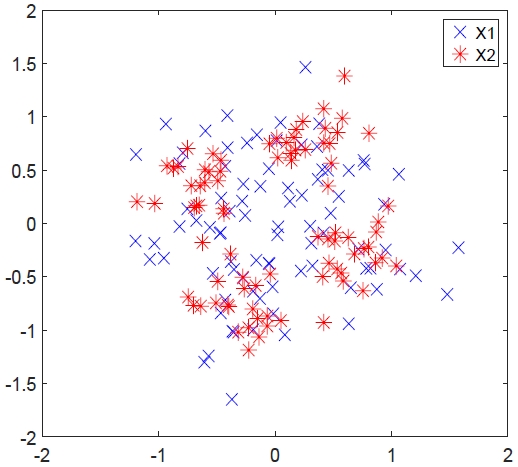
그림 2에는 U₁이 수신하는 hX₁과 hX₂가 도시되어 있다. X₁은 QPSK로 변조된 데이터 심볼이며, X₂는 16QAM으로 변조된 데이터 심볼이다. 신호 대 잡음비(Signal-to-Noise Ratio, SNR)는 10dB이다. 서브프레임마다 존재하는 제어 및 파일럿 신호를 고려하지 않고, 하나의 슬롯이 7개의 OFDM 심볼로 구성되어있다고 할 때, X₁과 X₂는 공통적으로 84개의 QPSK 및 16QAM 심볼들을 포함한다. 하나의 슬롯이 84개의 심볼만으로 구성되는 것은 PCE의 성능이 데이터 심볼의 수가 증가함에 따라 개선된다는 것을 고려할 때 보수적인 설정이라고 볼 수 있다. 왜냐하면 이것은 4G와 5G 시스템에서 하나의 UE에 할당할 수 있는 최소 자원요소(Resource Element)수이기 때문이다.

Fig. 2.

X1(QPSK) and X2(16QAM) received by U1

이 설정에서 PCE는 가장 낮은 채널 추정 성능을 보일 수밖에 없으므로 제안하는 기법의 최저 한계 성능을 검증하는 것에 적합하다고 할 수 있다. 타 단말 신호(Other UE Signal, OUS)를 이용한 PCE 채널 추정을 OUS-PCE로 명명하기로 한다.

3.2 OUS-PCE의 채널 추정

하향링크에서 신호를 수신하는 U₁는 하나의 서브프레임 내의 두 개의 슬롯에서 각각 다른 변조기법이 적용된 자신의 신호와 다른 사용자의 신호 X를 수신한다. 자신의 데이터 신호와 다른 단말의 데이터 신호를 포함하고 있는 수신된 신호는 SKC에 의하여 단계별로 군집화 된다[7][8]. SKC는 K-means 군집화를 이용하며, 4G와 5G에서 사용되는 M-ary 신호의 M이 4에 대한 거듭제곱들의 집합임에 착안하여 K-means 연산을 순차적으로 시행하면서 1회 K-means 연산 시 1개의 군집을 4개의 군집으로 분할한다[7]. 예를 들어 수신된 신호가 64QAM이고 최초 구분되지 않은 상태에서 하나의 군집으로 주어졌을 때, SKC는 3차에 걸친 K-means 연산 과정을 통해서 하나의 군집을 4의 세제곱인 64개의 군집으로 분할할 수 있다. M-ary 신호에 SKC를 적용할 때 필요한 K-means 연산 차수는 다음과 같이 계산될 수 있다[8].

$\[ S_M={\log }_4\left(M\right) \]$

(1)

그러나 수신 신호 y에서 각 슬롯에 있는 신호는 다른 변조기법으로 변조되어 있으므로, SKC를 적용할 때 S_M값을 하나로 정할 수 없다는 문제가 있다. X₁ 과 X₂의 변조 기법에 따라 M₁과 M₂가 다르기 때문이다. 본 연구의 목적은 PCE에서 K-means를 이용하여 채널을 추정함에 있어 입력으로 사용할 수 있는 심볼 수를 증가시키려는 것이기 때문에, 각 슬롯에 대해서 별도의 군집화 연산을 수행하는 것은 의미가 없다. 따라서 M₁과 M₂ 중 어느 하나를 선택하여 K-means 군집화를 진행할 수 있다.

첫 번째 방법은 M₁과 M₂ 중 더 작은 값을 갖는 변조기법을 기준으로 다음과 같이 선택한 값에 의해서 SKC를 동작시키는 것이다.

$\[ S_{M_{\mathrm{m}\mathrm{i}\mathrm{n}}}={\log }_4\left(\min \left(M_1,M_2\right)\right) \]$

(2)

식 (2)에서 min()은 괄호 안의 값들 중 가장 작은 값을 의미한다. 예를 들어 X₁이 QPSK 신호이고 X₂가16QAM 신호일 경우에 M₁ = 4과 M₂ = 16이므로 수신신호 y를 QPSK 변조기법에 맞추어 SKC를 통한 군집화를 진행한다.

두 번째, M₁과 M₂ 중 변조 차수가 더 큰 값을 다음과 같이 선택하여 SKC를 동작시키는 것이다.

$\[ S_{M_{\mathrm{m}\mathrm{a}\mathrm{x}}}={\log }_4\left(\max \left(M_1,M_2\right)\right) \]$

(3)

max()은 괄호 안에 있는 값들 중 최대 값을 선택하는 연산을 의미한다. 위와 동일한 예에서, X₁와 X₂가 각각 QPSK와 16QAM으로 변조되어 있을 때 수신 신호 y를 16QAM으로 보고 SKC를 통한 군집화를 진행한다.

SKC의 S_M번째 차수의 K-means 연산이 종료되었을 때, 최종적으로 형성된 군집들의 중심점은 다음과 같이 표현할 수 있다.

$\[ R_i^{S_M}\left(l\right),l\in \left\{1,\dots ,4^{S_M-1}\right\} \]$

(4)

i는 SKC의 최초 K-means 연산에 의하여 형성된 4 개의 군집에 대한 색인(Index)이다. 본 논문에서 채널추정에 이용하는 기준 중심점(Reference center) $$ R_C^{S_M}\left(i\right)$$은 각 i 군집사분면 기준 심볼(Reference symbol)들의 평균값으로 다음과 같이 계산될 수 있다.

$\[ R_C^{S_M}\left(i\right)=E\left[R_i^{S_M}\left(l\right)\right],l\in \left\{1,\dots ,4^{S_M-1}\right\} \]$

(5)

식 (5)에서 E[•]는 산술 평균 연산을 의미한다.

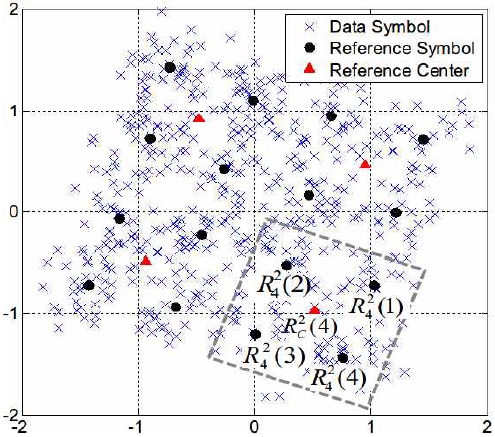
그림 3에 16QAM 데이터 심볼이 수신되었을 때, SKC의 동작이 도시되어 있다. 전체 심볼은 1차 K-means 연산을 통하여 4개의 군집으로 분할되고, 네 번째 군집을 점선 사각형으로 표시하였다. 각 군집은 다시 2차 K-means연산을 통해서 4개의 군집으로 분할되어 최종적으로 16개의 군집으로 분할된다.

Fig. 3.

SKC process for 16QAM

16QAM이므로 네 번째(i=4) 군집에 K-means 연산에 의하여 4개의 기준 심볼들이 계산되고, 이 기준 심볼들로부터 기준 중심점을 계산할 수 있다. 그림 3에서 볼 수 있는 바와 같이 기준 중심점은 채널 h의 위상(Phase)와 크기(Amplitude)를 반영하고 있기 때문에 최초 전송된 데이터 심볼의 종류를 알면 채널은 다음과 같이 추정할 수 있다[8].

$\[ \widehat{h}=E\left[R_C^{S_M}\left(i\right)/D^{S_M}\left(i\right)\right],i\in \left\{1,\mathrm{2,3},4\right\} \]$

(6)

D^S_M(i)는 QPSK(S_M = 1), 16QAM(S_M = 2), 64QAM (S_M = 3), 256QAM(S_M = 4)에 대해서 각각 다음과 같다.

$\[ \begin{array}{c}{D}^1\left(i\right)=e^{\left(2i-1\right)\pi /4}\hfill \\ D^2\left(i\right)={2\sqrt{10}/5\cdot e}^{\left(2i-1\right)\pi /4}\hfill \\ D^3\left(i\right)={4\sqrt{21}/21\cdot e}^{\left(2i-1\right)\pi /4}\hfill \\ D^4\left(i\right)={16\sqrt{170}/81\cdot e}^{\left(2i-1\right)\pi /4}\hfill \end{array} \]$

(7)

Ⅳ. 신호별 채널 추정 성능 평가 및 분석

본 논문에서 제안하는 채널추정기법의 성능을 검증하기 위하여 추정된 채널의 MSE를 측정하였다. MSE는 아래와 같은 식에 의해서 계산될 수 있다.

시스템 모델에 제시한 프레임 구조와 동일한 자원 블록을 사용하였고, 보수적인 성능검증을 위하여 X₁과 X₂가 포함하는 데이터 심볼 수는 각각 84 개다. X₁과 X₂의 변조기법에 따라서 식 (2)와 (3)의 두 가지 SKC를 적용하여 추정한 채널에 대한 MSE가 도시되어 있다.

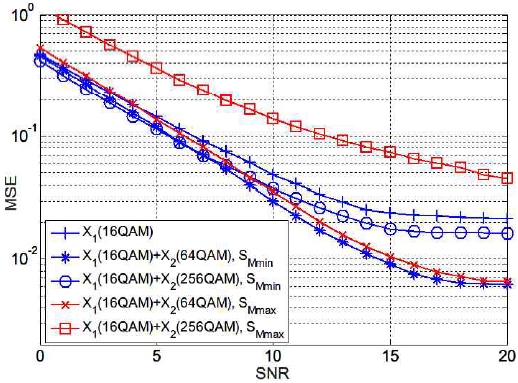
그림 4 ~ 6에서 식 (2)에 의한 것은 S_Mmin으로 표시하였고, 식 (3)에 의한 것은 S_Mmax으로 표시하였다. 본 연구는 하나의 UE에 할당된 무선 자원이 매우 적은 상황에서 PCE 채널 추정 성능을 개선하기 위한 연구로써, 하나의 슬롯에서 전송할 수 있는 데이터 심볼의 수가 최대 84개에 불과하므로 64QAM과 256QAM에 대해서 군집을 형성할 수 없어 X₁이 QPSK와 16QAM인 경우에 대해서 실험을 진행하였다.

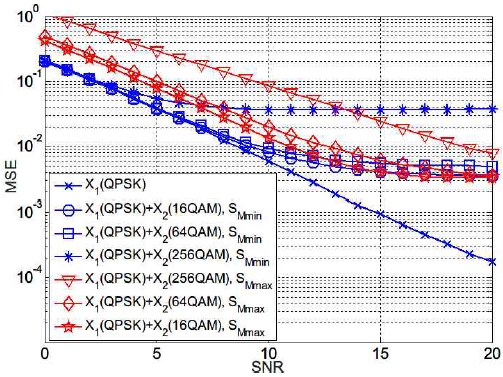
그림 4에는 QPSK 심볼만을 사용하여 추정한 채널의 MSE와 QPSK심볼과 16QAM 이상의 고차 변조되어 전송되는 심볼을 결합하여 추정한 채널의 MSE들이 도시되어 있다. 결과를 살펴보면, QPSK 심볼만으로 채널을 추정하였을 때 채널을 가장 정확하게 추정할 수 있다. 따라서 QPSK로 변조된 데이터 심볼을 수신할 때, 다른 UE의 데이터 심볼을 활용할 필요는 없다. 두 번째로 관찰할 수 있는 결과는 QPSK가 선택되어 전송되는 낮은 SNR 영역에서 일관되게 식 (2)의 S_Mmin에 의한 채널 추정 방법이 더 정확한 채널 추정 성능을 보인다는 것이다.

Fig. 4.

Other UE’s symbol utilization for channel estimation of U1 using QPSK

SNR 약 13dB에서 MSE 성능 역전 현상이 발생하는 것은 고차 변조 기법일수록 높은 SNR 영역에서 군집이 정확하게 형성되기 때문인 것으로 판단된다[7]. 이 실험 결과로부터 QPSK 데이터 심볼 수신 시, 해당 슬롯에 대해서 단독으로 PCE를 동작하는 것으로부터 가장 적확한 채널 추정이 가능함을 알 수 있다. 다른 UE의 심볼을 사용할 때, 다른 UE 데이터 심볼의 변조 차수와 상관없이 QPSK를 기준으로 SKC에 의한 채널 추정을 함으로써 채널 추정 오차를 감소시킬 수 있다.

그림 5는 U₁이 16QAM을 사용하는 경우에 U₂의 데이터 심볼을 이용한 채널 추정 결과를 보여주고 있다. U₁과 U₂가 수신한 심볼의 종류 조합이 동일하다면 그림 4의 결과와 동일하게 S_Mmin를 선택하였을 때 채널 추정 성능이 S_Mmax를 선택하였을 때 대비 우수하다. 따라서 다른 UE의 심볼의 종류가 무엇인지 상관없이 현재 U₁이 수신하고 있는 변조 차수에 기준을 두고 SKC를 진행하면 된다. 따라서 U₂ 데이터 심볼의 변조 방법에 대한 정보를 획득할 필요가 없다.

Fig. 5.

MSE of PCE for U1 with 16QAM and U2 data symbols

다음으로 그림 4의 결과와는 달리 U₁이 16QAM을 사용할 때에는 단독 채널 추정을 하는 것 보다 U₂의 데이터 심볼을 PCE에 활용하는 것이 채널 추정 성능을 개선할 수 있음이 실험을 통해 밝혀졌다.

16QAM 성상도에 16개의 서로 다른 심볼 위치가 있기 때문에 84개의 심볼만으로 PCE를 동작시키면 하나의각 심볼 위치가 평균 5.25개의 심볼만으로 이루어진 군집에 의해서 결정될 수 있어야 한다. 하나의 군집에 포함되는 평균 심볼 수 자체도 매우 적지만, 확률적으로 어떤 심볼 위치에 대한 군집에 단 하나의 데이터 심볼도 포함되지 않을 가능성이 존재한다[7][8]. 따라서 16QAM에 대한 PCE 성능 개선을 위하여 데이터 심볼 수의 실질적인 증가 효과를 얻을 수 있는 이 연구의 핵심 결과는 그림 5에 도시되어 있다고 볼 수 있다.

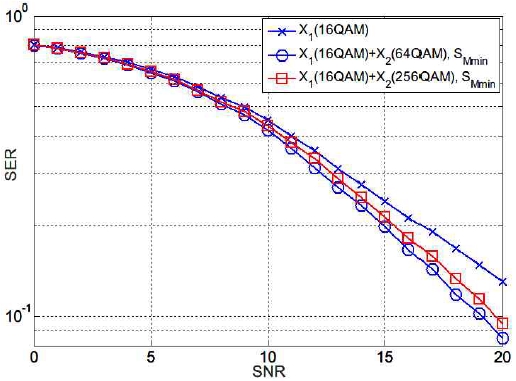
그림 6에는 채널 추정 시 U₂의 데이터 심볼 사용 유무 및 SKC를 동작시키기 위한 변조기법 기준 식 (2)와 (3)에 따른 U₁의 SER이 도시되어 있다. 그림 5의 채널 추정 정확도의 차이가 SER 성능 차이에 반영됨을 알 수 있다.

Fig. 6.

SER of U1 with PCE utilizing U2 data symbols

즉 한 UE가 매우 작은 데이터를 전송하게 되어 매우 적은 수의 데이터 심볼을 전송하게 될 때 16QAM을 사용하게 된다면, 다른 UE의 심볼을 활용하여 PCE의 채널 추정 성능을 개선할 수 있고, 채널 추정의 성능 차이는 SER 성능도 개선할 수 있음을 알 수 있다.

V. 결 론

기존 PCE 기법은 수신되는 데이터 심볼들이 성상도 상의 모든 심볼 위치에 고르게 분포해야만 정상적으로 채널을 추정할 수 있다는 문제를 가지고 있었다. 이 문제를 해결하기 위해서 본 논문에서는 하향링크에서 자신의 신호와 다른 UE의 신호를 함께 수신하여 채널을 추정하는 PCE 기법을 제안하였다. 두 단말의 데이터 심볼이 서로 다른 변조기법으로 변조되었을 때, 현재 PCE를 수행하는 단말의 신호가 변조된 기법으로 SKC를 수행함으로써 16QAM 데이터 심볼로 추정한 채널의 MSE를 개선하고 SER을 감소시킬 수 있었다. 적은 데이터량을 보내야 하는 상황에서 PCE를 동작시킬 때 채널 추정 성능을 개선할 수 있는 연구 결과가 도출되었으며, 향후 본 연구를 확장하여 데이터 전송량이 적은 이동 기계간 통신(mMTC, mobile Machine Type Communication) 응용 기술에 적용할 계획이다.

Acknowledgments

이 논문은 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2018R1D1A1B07050143)

References

• H. Chen, J. Wu, and T. Shimomura, "New Reference Signal Design for URLLC and eMBB Multiplexing in New Radio Wireless Communications", 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, pp. 1220-1225, Sept. 2018. [https://doi.org/10.1109/PIMRC.2018.8580882]
• R. Apelfrojd, W. Zirwas, and M. Sternad, "Low-Overhead Cyclic Reference Signals for Channel Estimation in FDD Massive MIMO", IEEE Transactions on Communications, Vol. 67, No. 5, pp. 3279-3291, Jan. 2019. [https://doi.org/10.1109/TCOMM.2019.2895059]
• K. Upadhya, Sergiy A. Vorobyov, and M. Vehkapera, "Downlink performance of superimposed pilots in massive MIMO systems in the presence of pilot contamination", IEEE Transactions on Wireless Communications, Vol. 17, No. 10, pp. 6630-6644, Oct. 2018. [https://doi.org/10.1109/TWC.2018.2861770]
• J. Shen, J. Zhang, and Khaled B. Letaief, "Downlink User Capacity of Massive MIMO Under Pilot Contamination", IEEE Transactions on Wireless Communications, Vol. 14, No. 6, pp. 3183-3193, Jun. 2015. [https://doi.org/10.1109/TWC.2015.2403317]
• H. Wang, "Performance Evaluation of Channel Estimation Scheme Using Clustering Algorithm", Journal of KIIT, Vol. 16, No. 2, pp. 61-66, Feb. 2018. [https://doi.org/10.14801/jkiit.2018.16.2.61]
• K. Jung and H. Wang "Pilotless Channel Estimation Scheme using Clustering-based Unsupervised Learning", 2018 15th International Symposium on Wireless Communication Systems (ISWCS), Lisbon, Portugal, pp. 1-5, Aug. 2018. [https://doi.org/10.1109/ISWCS.2018.8491198]
• K. Jung and H. Wang, "Higher-order Modulation Signal Detection Scheme Using Sequential Clustering", Journal of KIIT, Vol. 17, No. 3, pp. 87-93, Mar. 2019. [https://doi.org/10.14801/jkiit.2019.17.3.87]
• H. Wang, "Channel Estimation Scheme for High-Order Modulation Using Sequential K-means Clustering", Journal of KIIT, Vol. 17, No. 6, pp. 95-102, Jun. 2019. [https://doi.org/10.14801/jkiit.2019.17.6.95]
• Coates A., Ng A. Y, "Learning Feature Representations with K-Means", Lecture Notes in Computer Science, Vol. 7700, pp. 561-580, 2012. [https://doi.org/10.1007/978-3-642-35289-8_30]
• E Dahlman, S. Parkvall, and J. Skold, "5G NR: The Next Generation Wireless Access Technology 1st Edition", Academic Press, 2018. [https://doi.org/10.1016/B978-0-12-814323-0.00001-6]
• E Dahlman, S. Parkvall, and J. Skold, "4G, LTE-Advanced Pro and The Road to 5G", Academic Press, 2016.
• J. Kim, B. Yeo, H. Choi, and K. Kim, "Estimation and Analysis of MIMO Channel Parameters using the SAGE Algorithm", The Journal of IIBC, Vol. 17, No. 5, pp. 79-84, Oct. 2017.
• B. Sklar, "Digital Communications: Fundamentals and Applications 2nd Ed", PrenticeHall, 2001.