다중 GPU 사용을 위한 CUDA C 행렬의 곱 프로그램의 구현

Ⅰ. 서 론

그래픽 장치인 GPU(Graphic Processing Unit)를 일반 연산에 사용하는 GPGPU(General Purposed GPU, 이하 GPU)는 2차원의 배열 구조를 가지고 있는 수백 개의 코어를 병렬로 계산하기 때문에 CPU에 비교하여 투자비용 대비 계산 성능이 뛰어나 HPC(High Performance Computing) 분야에서는 중요한 역할을 차지하고 있다[1].

행렬의 곱 프로그램은 수치해석 분야에서 가장 대표적인 프로그램의 하나로서 성능 벤치마킹을 비롯한 다양한 응용 프로그램에서 사용되고 있다. 하지만 이 프로그램은 병렬처리를 위해서는 곱하고자 하는 두 행렬에서 행과 열의 데이터를 각각 사용하기 때문에 분산메모리형의 병렬컴퓨터에서는 구현이 어려운 알고리즘 중의 하나이다[2]. 단일 GPU에서는 캐시메모리의 역할을 하는 공유메모리를 사용하여 효율적인 병렬프로그램의 구현이 가능하다[3]. 하지만 병렬컴퓨터에서 다중 GPU를 장착하는 경우에는 GPU 간에 데이터 전송이 필요하기 때문에 효율적인 병렬프로그램의 구현이 필요하다[4].

GPU를 사용하여 행렬의 곱을 계산하는 프로그램에 대한 연구는 활발히 진행되고 있다. Nvidia CUTLASS(CUDA Templates for Linear Algebra Subroutines)의 GEMM(GEneral Matrix Multiplication)은 타일 형식으로 공유메모리를 사용하여 단일 GPU를 위한 블록 행렬의 곱 프로그램을 구현하였다[5]. 다중 GPU를 위한 프로그램으로는 [6]에서는 GEMM을 다중 GPU에서 본 논문에서 사용한 Fox 알고리즘과 유사한 방식으로 사용하였고, [7]에서는 범용이 아닌 특수한 형태의 행렬의 곱을 위한 프로그램을 구현하였다. 또한 [8]에서는 다중 GPU 상에서 공유메모리형의 병렬프로그램 방식인 OpenMP를 사용하여 행렬의 곱을 구현하였다. 본 연구와의 비교 요약은 표 1과 같다.

Table 1.

Comparison with our method

본 연구에서는 병렬컴퓨터의 여러 노드에 분산된 다중 GPU에서의 행렬의 곱 프로그램을 위한 알고리즘을 Nvidia CUDA(Compute Unified Device Architecture) C 언어로 구현하였다. CUDA 프로그램은 단일 GPU에서는 Fox 알고리즘을 응용하여 캐시메모리의 역할을 하는 공유메모리를 사용하여 성능의 효율성을 높였으며, 다중 GPU를 사용하기 위하여 Cannon 알고리즘을 응용하여 MPI(Message Passing Interface)를 통하여 GPU 간에 데이터를 전송하였다. 구현된 프로그램은 기존의 프로그램과는 다르게 대표적인 병렬 행렬의 곱 알고리즘들을 사용하여 쉽고 효율적인 성능을 가질 수 있도록 구현하였다.

본 논문의 구성은 다음과 같다. 2장에서는 행렬의 곱 계산을 위한 병렬 알고리즘과 CUDA 병렬프로그램의 구현에 대한 설명하고 3장에서는 다중 GPU에서의 실행 결과와 성능에 대해 분석한다. 마지막으로 4장에서는 결론으로 맺는다.

Ⅱ. 병렬 행렬의 곱 CUDA 프로그램의 구현

이 장에서는 프로그램에 사용된 병렬 알고리즘들의 이론적인 배경과 이들을 적용한 CUDA 프로그램의 구현에 대하여 설명한다.

2.3 Cannon 알고리즘

다중 GPU에서의 실행을 위한 병렬 행렬의 곱 알고리즘은 Cannon 알고리즘을 사용하였다[11][12]. Cannon 알고리즘은 L. Cannon이 2차원 정방행렬 곱셈을 위해 개발한 병렬 행렬의 곱 알고리즘으로서 이론적으로는 가장 효율적인 알고리즘으로 알려져 있다. Fox 알고리즘에서는 1번째 스텝에서 행으로 방송하는 과정에서 해당 프로세서들만 통신에 가담하기 때문에 휴지 프로세서가 발생하는 비효율이 존재하는 반면에 Cannon 알고리즘은 점대점(Peer-to-peer) 통신만 사용하기 때문에 휴지 프로세서가 존재하지 않는다. 한편 Cannon 알고리즘은 정방형 행렬만 사용하고 초기에 행렬 A와 B를 재배치해야 하는 단점이 있다. 하지만 본 연구에서는 입력 행렬을 CPU에서 GPU로 초기에 분할하는 과정에서 재배치하기 때문에 이러한 단점을 극복하였다. 다음은 Cannon 알고리즘이다.

for i = 1 to N {
   step1: C += A x B
   step2: shift A west
   step3: shift B north
}

알고리즘은 3 스텝으로 구성이 되며 Fox 알고리즘과 마찬가지로 N번 반복한다. 알고리즘을 사용하기 이전에 행렬 A의 i 행의 값들을 모두 (i-1) 번만큼 왼쪽으로 이전 그리고 행렬 B의 i 열의 값들을 모두 (i-1)번 만큼 위로 이전한다.

Cannon 알고리즘에서는 예를 들어서 C₁₁ = A₁₂ × B₂₁, C₁₂ = A₁₃ × B₃₂와 같이 A 행렬과 B 행렬의 같은 자리를 연산하여 C 행렬을 계산한다. 모든 값 사이의 연산이 끝나면 A 행렬의 값들은 모두 왼쪽으로, B 행렬의 값은 위쪽으로 한 칸씩 이전하고 다시 연산을 진행한다.

다중 GPU를 사용하여 행렬의 곱을 계산하기 위한 Cannon 알고리즘을 구현한 CUDA 프로그램은 다음과 같다.

int main(){
   ...
   MPI_Init.);
   ...
   for i = 1 to N {
      matmul(A, B, C);
      MPI_SendRecv(...,A,...);
      MPI_SendRecv(...,B,...);
      cudaThreadSynchronize();
   }
   ...
   MPI_Finalize();
}

위에서 matmul()은 2.2에서 구현된 Fox 알고리즘을 사용한 행렬의 곱 프로그램이다, 프로그램은 MPI(Message Passing Interface)[13] 병렬 프로그램으로서 GPU는 각 프로세스에서 사용하며 GPU간의 행렬 A, B를 shift하는 함수는 MPI_SendRecv()를 사용하였다. shift을 실행한 이후에는 모든 GPU가 동시에 작업을 수행할 수 있도록 쓰레드 동기화 함수인 cudaThreadSynchronize()를 실행하였다.

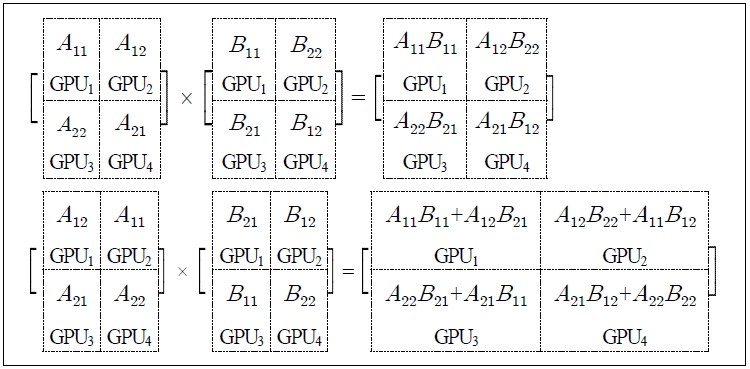
그림 1은 4개의 GPU를 사용한 행렬의 곱 프로그램의 실행 과정을 보여준다. 행렬 A와 B를 4개의 GPU에 2×2 서브 블록으로 분할하였으며 초기의 Cannon 알고리즘을 사용하기 위한 형태로 하여 각 GPU에 할당하였다. 프로그램은 2번의 반복 이후에 행렬의 곱을 계산하였다.

Fig. 1.

Matrix multiplication on four GPUs

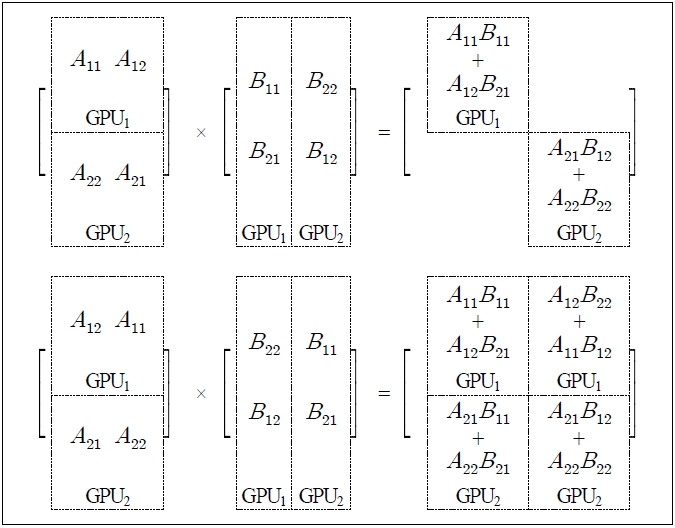
한편 Cannon 알고리즘은 n²(n은 자연수) 형태의 정방형 프로세스의 수만 가능하기 때문에 2n(2, 4, 6, ...)의 프로세스를 사용하기 위하여 하나의 프로세스(GPU)가 한 개 이상의 분할된 서브 행렬을 할당하는 형식으로 프로그램을 수정하였다.

그림 2는 2개의 GPU를 사용하여 수정된 프로그램으로 행렬의 곱을 실행한 과정을 보여준다. 각 GPU는 2개의 서브 블록을 할당하여 계산하여 2번 반복으로 행렬의 곱 계산을 하였다.

Fig. 2.

Matrix multiplication on two GPUs

Ⅲ. 성능 및 분석

3.2 성능 분석

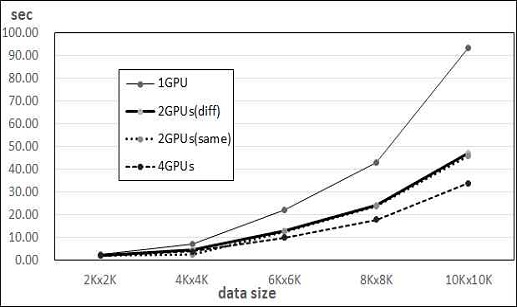
CUDA 프로그램은 각 GPU에서 256개의 쓰레드를 사용하였다. 그림 3은 병렬 행렬의 곱 프로그램의 실행시간을 GPU의 수에 따라 비교하였다. 사용된 행렬의 크기는 2K×2K, 4K×4K, 6K×6K, 8K×8K, 10K×10K 등이다. 프로그램의 실행에는 GPU를 1개, 2개 그리고 4개를 사용하였으며, 2개를 사용하는 경우에는 통신 부하의 영향을 알아보기 위하여 동일한 노드에 있는 경우와 네트워크로 연결된 다른 노드에 있는 경우에서 따로 실행하였다. GPU를 1개 사용한 경우에는 Nvidia CUTLASS의 GEMM의 성능과 거의 유사한 성능을 보였다. 두 프로그램 모두 캐시메모리 역할을 하는 공유메모리를 효율적으로 사용한 결과로 보여 진다.

Fig. 3.

Execution time comparison using different number of GPUs

그림에서와 같이 계산 성능은 1개의 GPU를 사용한 경우에 비교하여 다중 GPU의 계산이 GPU의 수에 따라 효율적인 것을 볼 수 있으며 행렬의 크기가 클수록 성능의 개선이 증가함을 알 수 있다. 한편 2개의 GPU를 사용하는 경우에 하나의 노드에 있는 경우와 다른 노드에 있는 경우에는 통신 부하가 적기 때문에 동일한 노드의 경우가 성능이 낫긴 하지만 차이가 크지 않아서 네트워크상의 통신 부하의 영향이 크지 않음을 알 수 있다.

GPU는 PCI(Peripheral Component Interconnect) Express를 통하여 컴퓨터와 연결이 되어 있는데 PCI Express는 입출력을 위한 직렬 구조의 인터페이스로서 데이터의 전달 속도가 컴퓨터 내부의 병렬 버스 구조에 비교하여 현저히 떨어진다[15]. GPU에서 계산을 하기 위하여 CPU로부터 데이터를 복사하여야 하며, 또한 다중 GPU를 사용하기 위해서는 GPU에서 다른 GPU로 데이터를 전송하기 위해서도 CPU의 메모리로 복사하여야 한다. 따라서 CPU와 GPU간의 데이터 전송 부하가 성능에 영향을 미치게 되며, 특히 다중 GPU를 사용할 경우에는 선형의 성능 개선은 기대하기 어렵게 된다.

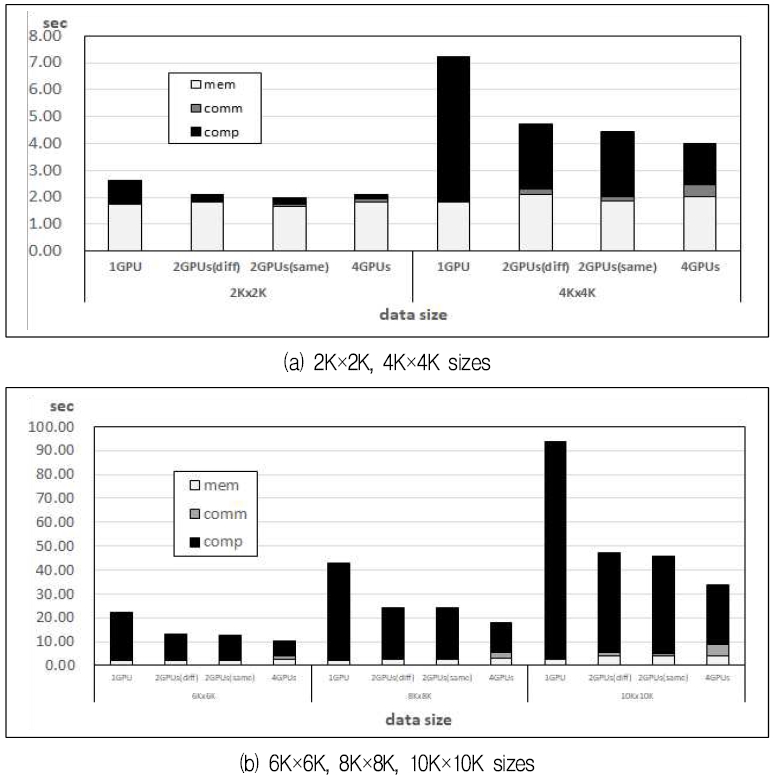
본 연구에서는 다중 GPU의 계산 성능을 보다 자세히 분석하기 위하여 실행 시간에서 CPU와 GPU간의 메모리 데이터 전송 시간과 MPI 통신 시간을 분리하여 측정하였다. 그림 4의 (a)는 행렬의 크기가 2K×2K와 4K×4K인 경우를 각 구성 요소에 대하여 비교하였다. 그림에서 볼 수 있듯이 행렬의 크기가 작은(2K×2K) 경우에는 다중 GPU의 사용이 성능의 개선에 영향이 거의 없음을 알 수 있다. 이는 기본적인 CPU와 GPU 간의 데이터 전송 시간이 전체 실행 시간에서의 비중이 크고, 또한 전체 GPU의 각 쓰레드에서 계산하는 데이터가 작기 때문에 다중 GPU를 사용한 성능 개선이 거의 없기 때문이다. 한편 데이터의 크기가 4K×4K인 경우에는 데이터 전송 시간의 비율이 낮기 때문에 성능의 개선을 볼 수 있다.

Fig. 4.

Execution time comparison by components

그림 4의 (b)는 행렬의 크기가 6K×6K, 8K×8K, 10K×10K인 경우를 비교하였다. 행렬의 크기가 커질수록 데이터 전송 시간의 비중이 낮아지기 때문에 GPU의 수가 많아질수록 성능의 개선이 커지는 것을 볼 수 있다.

한편 그림 4의 (a)와 (b)에서 볼 수 있듯이 MPI 통신 시간에 따른 부하는 4개의 GPU의 경우를 제외하고는 전체적인 성능에 거의 영향이 없는 것을 볼 수 있다.

Ⅳ. 결 론

본 연구에서는 다중 GPU를 사용하기 위한 행렬이 곱 병렬 프로그램을 CUDA C 언어로 구현하였다. 병렬 프로그램은 GPU 내에서는 Fox 알고리즘을 사용하였고 다중 GPU를 위한 계산은 분산메모리형 컴퓨터의 병렬 알고리즘인 Cannon 알고리즘을 사용하였다.

다중 GPU를 사용하는 경우에는 CPU와 GPU 간의 데이터 전송 시간이 성능에 병목이 될 수 있기 때문에 이 지연 시간을 줄이기 위하여 동일 보드(온보드)상의 다중 GPU의 필요성이 증가한다. 하지만 온보드에 장착되는 GPU 수의 한계가 있기 때문에 CPU를 통한 GPU 간의 데이터 전송은 불가피하다. 이에 본 연구에서는 이 지연 시간이 행렬의 크기와 성능에 미치는 영향을 알아보기 위하여 CPU와 GPU 간의 데이터 전송 시간을 분리하여 분석하였다. 성능 분석 결과 CPU와 GPU 간의 데이터 전송에 따른 지연시간이 영향을 주는 작은 크기의 행렬을 계산하는 경우에는 성능의 개선에 큰 영향이 없었지만 행렬의 크기가 일정 크기 이상인 경우에 행렬의 크기가 클수록 다중 GPU를 사용한 성능의 개선이 효율적이었다. 예를 들어 8Xx8K 및 10Kx10K의 크기의 행렬을 4개의 GPU를 사용한 결과 1개 대비 2.5배와 2.8배 이상의 성능 개선(70%의 효율성)을 보였다. 한편 MPI를 사용한 CPU간의 네트워크에 의한 통신 지연에 따른 부하는 성능에 거의 영향을 주지 않는 것을 알 수 있다. 또한 GPU의 수를 증가시켜 계산한 결과 GPU의 수가 증가할수록 계산 시간이 GPU의 수에 비례하여 감소하는 모습을 보였다.

References

• Y. Kim and T. Kang, "CUDA Parallelization of the Smallest-Small-World Cellular Genetic Algorithms", Journal of KIIT. Vol. 16, No. 1, pp. 19-26, Jan. 2018. [https://doi.org/10.14801/jkiit.2018.16.1.19]
• H. Cohn, R Kleinberg, B Szegedy and C. Umans, "Group-theoretic Algorithms for Matrix Multiplication", Proceedings of the 46th Annual Symposium on Foundations of Computer Science, pp. 379-388, Oct. 2005.
• D. Yuen, ‎L. Wang, and ‎X. Chi, "GPU Solutions to Multi-scale Problems in Science and Engineering", Springer, pp. 207, 2013. [https://doi.org/10.1007/978-3-642-16405-7]
• V. Kindratenko, J. Enos, G. Shi, and M. Showerman, "GPU clusters for high-performance computing", Proceedings of the 2009 IEEE International Conference on Cluster Computing, pp. 1-8 Aug. 2009. [https://doi.org/10.1109/CLUSTR.2009.5289128]
• CUTLASS: Fast Linear Algebra in CUDA C++, Nvidia. Dec. 2017.
• T. Herault, Y. Robert, G. Bosilca, and J. Dongarra, "Generic Matrix Multiplication for Multi-GPU Accelerated Distributed-Memory Platforms over PaRSEC", 2019 IEEE/ACM 10th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems, pp. 33-41, 2019. [https://doi.org/10.1109/ScalA49573.2019.00010]
• J. Chen, N. Xiong, X. Liang, D. Tao, S. Li, K. Ouyang, K. Zhao, N. A DeBardeleben, Q. Guan, and Z. Chen, "Optimizing tall-and-skinny matrix-matrix multiplication on GPUs", Proceedings of the ACM International Conference on Supercomputing, pp. 106–116, Jun. 2019.
• M. Duaimi, F. Abbas, J. AL-Gburi, A. Ehsan, A Al-Zubaidi, and I. Al-Jadir, 4, "Implementing Multithreaded Programs using CUDA for GPGPU to Solve Matrix Multiplication", Journal of Xi'an University of Architecture & Technology, Vol XII, Issue III, pp. 3083-3089, 2020.
• R. White, "Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI", CRC Press, pp. 381, 2015. [https://doi.org/10.1201/b19005]
• G. C. Fox, S. W. Otto, and A. J. G. Hey. "Matrix Algorithms on a Hypercube I: Matrix Multiplication", rallel Computing, Vol. 4, No. 1, pp. 17-31, 1987. [https://doi.org/10.1016/0167-8191(87)90060-3]
• L. E. Cannon, "A cellular computer to implement the Kalman Filter Algorithm", Ph.D. Thesis, Montana State University, July 1969.
• T. Sterling and M. Brodowicz, M. Anderson, "High Performance Computing: Modern Systems and Practices", Morgan Kaufmann, pp. 301, 2017. [https://doi.org/10.1016/B978-0-12-420158-3.00018-6]
• The University of Tennessee, “MPI: A Message Passing Interface Standard", Version 3.1, Message Passing Interface Forum, Jun. 2015.
• Tesla C1060 Installation guide, Nvidia, 2008.
• I, Lee and H. Cho, "A Study of solving the bottleneck between CPU and GPU", Proceedings of the Korean Society of Computer Information Conference, pp. 3-4, Jul. 2020.