열화상 영상 잡음 제거를 위한 효율적인 잡음 제거 블록 기반의 신경망
; 황성민*
; 보호앙트롱*
; 당탄부*
; 후이트완녁*
; 이주환*
; 신도성*
; 김진영**
; Seongmin Hwang*
; Vo Hoang Trong*
; Dang Thanh Vu*
; Huy Toan Nguyen*
; JooHwan Lee*
; Dosung Shin*
; Jinyoung Kim**
초록
열화상 카메라는 제한된 열화상 해상도로 인해 잡음이 있는 영상을 야기한다. 본 논문에서는 잡음 문제를 해결하기 위해 반복 가능한 인셉션-레지듀얼 블록(IRB)으로 이루어진 새로운 딥러닝 기반의 신경망을 제안한다. 각각의 IRB는 원본 이미지에 대하여 서로 다른 수용 영역을 가진 합성곱 층 2개를 가지고 베니싱 그레디언트(vanishing gradient)를 방지하기 위한 하나의 쇼트 컷(shortcut connection)으로 구성된다. 제안된 방법은 12개의 열화상 이미지로 테스트가 이루어졌다. 실험 결과, 제안된 방법은 최신의 잡음 제거 방법인 DnCNN과 비교해 봤을 때 신호대잡음비(PSNR)를 39.57에서 40.26으로 처리속도는 1.5910초에서 0.7508초로 잡음 제거 성능 및 처리 속도 개선을 보여준다.
Abstract
Thermal cameras show noisy images due to their limited thermal resolution, especially for the scenes of a low-temperature difference. In order to deal with a noise problem, this paper proposes a novel neural network architecture with repeatable denoising inception-residual blocks(DnIRB) for noise learning. Each DnIRB has two sub-blocks with difference receptive fields and one shortcut connection to prevent a vanishing gradient problem. The proposed approach is tested for 12 thermal images. The experimental results indicate that the proposed approach shows the PSNR performance is increased 39.57 to 40.26 and processing time also is reduced 1.5910 to 0.7508 compared with state-of-the-art denoising methods which is called DnCNN.
Keywords:
image denoising, convolutional neural networks, thermal image, laplace noise, receptive field, residual leraningⅠ. 서 론
영상 처리에는 영상 분할, 분류, 탐지, 추적, 복구 및 행동 인식 등 다양한 응용 분야가 존재한다. 특히 영상 잡음 제거는 영상 처리를 위해 필수적으로 거쳐야 하는 단계이며, 지난 20년간 계속 발전해오고 있다. 가우시안 스무딩[1], 이방성(Anisotropic) 필터링[2][3], 모든 변화 최소화[4], 웨이브렛 임계값 방법[5][6], 그리고 BM3D[7]이 고전적인 영상 잡음 제거를 위한 방법들이다.
비국부적(Non-local) 알고리즘으로 영상 잡음 제거를 제안하는 방법으로는 BM3D[7], LSSC[8], NCSR[9]와 WNNM[10]이 대표적이다. 신뢰도 추론 방법(Belief propagation inference)과 마르코프 랜덤 필드(Markov random fields)를 혼합하여 영상 잡음 제거를 설명하거나, 3차원 데이터 배열에 대한 2차원 영상 세분화 유사 그룹 변환으로 영상 잡음에 대한 희소성을 향상시켰다. 이러한 선택과 추출 방법들은 잡음 제거에서 대단한 성과를 보였지만, 크게 2가지 단점이 있었다. 첫째, 위의 방법들은 볼록 행렬(Non-convex)이 아니기 때문에 수동으로 파라미터를 세팅해야 한다. 둘째, 테스트 단계에서 복잡한 최적화 문제와 결과를 위해 높은 계산량이 필요하다.
최근에 기존의 수동으로 파라미터를 세팅하는 방법과 달리, 깊은 신경망을 통해 자동으로 학습하고 효과적인 영상 특징을 찾게 되었다. 또한 딥러닝은 빅데이터와 그래픽 프로세싱 유닛(GPU, Graphics Processing Unit)을 통해 학습 능력이 향상되었다. 다층 퍼셉트론(MLP)[11]은 빅데이터 기반의 GPU를 사용하여 높은 영상 잡음 제거 성능을 보였다. 케스캐이드 수축 필드(CSF) [12]는 랜덤 필드 기반의 모델 생성과 알고리즘 최적화를 통해 영상 잡음 제거를 하였다. 학습할 수 있는 비선형 반응 확산 모델[13]은 경사 따라가기 알고리즘에 기반하여 확산 모델의 파라미터를 학습하여 영상 잡음을 시도하였다. 영상 잡음 제거 컨벌루션 네트워크(DnCNN)[14]는 배치 정규화(Batch normalization) 및 ResNet 구조를 활용하여 영상 잡음을 제거하였다.
이후에는 블록 매칭 기반의 알고리즘을 컨벌루션 네트워크에 혼합한 BMCNN[16]의 아이디어가 있었으며, 컨벌루션 네트워크를 위한 더 빠르고 유연한 해결책 기반의 영상 잡음 제거(FFDNet)[17]는 잡음 수준과 잡음 영상을 입력으로 사용하여 서로 다른 잡음 수준을 다뤘다. 이 방법은 하나의 모델이 다양한 잡음 수준을 다루는 것을 의미하고, 성능과 속도가 향상되었다. IRCNN[18]은 모델 기반의 최적화 방법과 컨벌루션 네트워크를 결합한 서로 다른 모델 2개를 하나의 모델로 사용하여 영상 잡음 문제를 해결하였다. 추가적으로 팽창(Dilated) 컨벌루션 필터를 네트워크에 사용하였다.
계속 발전하는 영상 잡음 제거 방법들은 다양한 시도를 통해 영상 잡음 제거 성능을 향상시켰지만 가시광 영상에 한정되어 있으며 처리 시간이 오래 소요된다. 또한 딥러닝 기반의 영상 잡음 제거 방법들은 전통적인 컨벌루션 네트워크의 구조를 바탕으로 인기가 있고 활용이 많이 되는 방법들을 사용하기 때문에 영상 잡음 제거에 최적화된 딥러닝 기반의 모델이 아닐 수 있다.
본 논문은 여러 개의 작은 블록으로 구성된 컨벌루션 네트워크 구조와 ResNet에서 사용된 쇼트컷(Shortcut)을 적용하여 기존 방법 대비 최고의 성능과 빠른 처리 속도를 보여준다. 열화상 카메라의 성능에 따라 촬영된 열화상 영상의 경우, 최저 및 최고 온도 차이가 2℃ 미만인 환경에서 촬영을 할 때, 아날로그에서 디지털로 변환하는 과정에서 샘플링과 양자화 문제로 인해 잡음이 발생하게 된다. 본 논문은 제안된 모델을 통해 이러한 열화상 잡음을 제거하는데 목적을 둔다.
본 논문은 2장에서는 열화상 영상의 잡음을 분석하고, 3장에서는 제안하는 전체 모델 구조 및 잔여 학습을 설명한다. 4장에서는 제안된 모델과 기존의 영상 잡음 제거 방법과 비교 실험 및 결과를 설명하고 5장에서는 결론을 설명하는 것으로 구성된다.
Ⅱ. 영상 잡음 정의
열화상 카메라로 열화상 영상을 얻을 때, 열화상 카메라 성능에 따라 차이는 존재하지만, 만약 촬영시의 최소 온도와 최고 온도 차이가 2℃ 미만일 경우 샘플링과 양자화 문제로 인한 열화상 영상 잡음이 발생하게 된다. BM3D 모델[7]의 잡음 추출기를 활용하여 촬영된 열화상 영상 잡음으로부터 잡음 히스토그램을 얻었다. 그림 1은 열화상 영상 잡음 확률밀도함수(pdf)를 각각 가우시안(Gaussian) 잡음 확률 밀도 함수와 라플라스(Laplace) 잡음 확률 밀도 함수와 비교한 것이다. 가로 축은 잡음 값이고 수직 축은 잡음 확률이다.
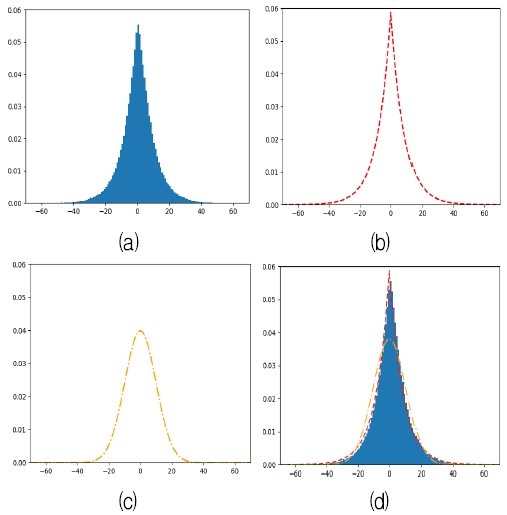
Comparison of thermal noise distribution, Gaussian and Laplace pdf, (a) Extracted thermal noise distribution pdf, (b) Laplace pdf, (c) Gaussian pdf, (d) Comparison of each pdf
특정한 조건 하에서 열화상 카메라를 통해 얻은 열화상 영상 잡음은 그림 1(a)이다. 열화상 영상 잡음은 -40부터 40까지의 범위에 잡음 값이 분포하며 0을 중심으로 잡음 확률이 밀집된 것을 확인할 수 있다. 그림 1(b)은 라플라스 잡음 확률밀도함수는 열화상 영상 잡음과 유사한 분포를 보이지만 그림 1(c)은 열화상 영상 잡음과 다른 분포를 보인다.
결과적으로 그림 1(d)에서처럼 열화상 영상 잡음 히스토그램과 라플라스 잡음 확률밀도함수(빨간선) 및 가우시안 잡음 확률밀도함수(파란선)을 겹쳐보았을 때, 열화상 영상 잡음은 라플라스 잡음과 유사하다는 것을 확인할 수 있었다. 위와 같은 관찰을 통해, 열화상 영상 잡음을 제거할 수 있는 모델을 학습할 때, 라플라스 잡음 확률 분포를 포함한 실험 결과를 포함하였고, 이와 관련된 내용은 4장에서 자세히 설명하겠다.
Ⅲ. 제안하는 모델
이번 장에서는 열화상 영상 잡음 제거를 위한 딥러닝 기반의 모델 구조를 소개하고, 제안된 모델에서 영상 잡음 제거에 가장 큰 기여를 하는 인셉션-레지듀얼 블록을 자세히 설명한다. 마지막으로 잔여 학습에 대해 기술한다.
3.1 전체 구조
그림 2는 제안하는 모델의 입력부터 출력까지 전체 구조를 보여준다. 제안하는 모델은 DnCNN 구조[14]로부터 영감을 받았지만 테스트 속도가 빠르고, 전통적이고 일반적인 컨벌루션 필터 및 층 대신 Inception-ResNet[15]에서 착안한 새로운 컨벌루션 구조로 영상 잡음 제거 성능도 개선하였다.
Proposed denoising model architecture
입력과 가까운 컨벌루션 층에서는 깊고 복잡한 필터를 사용하더라도 단순한 필터를 사용한 것과 특징맵이 크게 차이가 없기 때문에 수용 영역(Receptive field)과 연산량을 고려하여 첫 번째 컨벌루션 층에서는 7×7 필터를 64개의 채널로 사용하고, 두 번째 컨벌루션 층에서는 3×3 필터를 64개의 채널로 사용하였다. 이후 영상 잡음 제거를 위한 인셉션-레지듀얼 블록을 사용하고, 마지막에 3×3 단일 필터를 사용하여 출력을 얻을 수 있도록 한다.
모든 컨벌루션 층 사이는 컨벌루션 필터와 정류한 선형 유닛(ReLU)의 활성함수(Activation function)으로 구성되어 있으며, 풀링 층은 존재하지 않는다. 그 이유는 딥러닝 기반의 영상 잡음 제거에서는 원본 영상으로부터 얻는 특징 값에 대해 압축으로 낮은 수준의 특징 값을 잃을 수 있기 때문이다.
3.2 반복 가능한 인셉션-레지듀얼 블록
최근 딥러닝 분야에서 합성곱 신경망 기반의 모델들이 영상 분류 및 인식 분야에서 좋은 성능을 보여주고 있다. 그 중 Inception-Resnet 모델은 다양한 수용 영역과 쇼트컷을 포함하는 컨벌루션 층을 큰 특징으로 가지고 있다. 제안하는 모델의 반복 가능한 인셉션-레지듀얼 블록은 Inception-Resnet 모델로부터 영감을 받아 열화상 영상 잡음 제거에 특화될 수 있도록 수정하고 최적화하여 잡음 제거 성능 및 처리 속도를 개선하여, 이 유닛을 위와 같이 이름 짓게 되었다. 인셉션-레지듀얼 블록은 영상 잡음 제거 성능과 처리 속도의 목표에 따라 모델에서 개수를 조정할 수 있다.
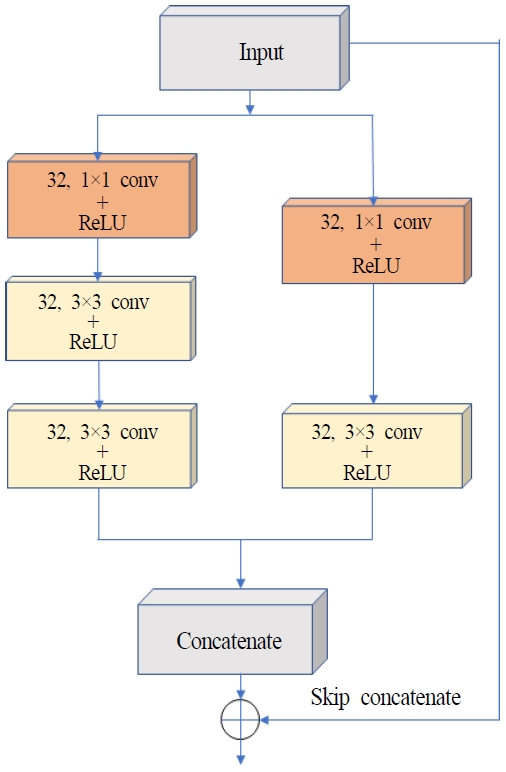
그림 3은 영상 잡음을 위한 인셉션-레지듀얼 블록 세부 구조를 보여준다. 인셉션-레지듀얼 블록의 입력은 각기 다른 2개의 컨벌루션 층 가지의 입력이 된다. 각각의 컨벌루션 층의 가지의 맨 상단에 위치한 1×1 컨벌루션 필터는 병목층(Bottleneck layer)의 특성으로, 입력 채널의 수를 64에서 32로 절반으로 감소시켜 모델 전체의 연산량을 줄이는 역할을 한다.
Repeatable denoising inception-residual block
그림 3에서 왼쪽의 가지는 1×1 컨벌루션 필터 이후에 3×3 필터를 포함하고, 오른쪽 가지는 3×3 필터 2개를 포함하게 되는데 왼쪽 가지는 특징맵에 대해서 3×3의 수용 영역을 가지는 역할을 하고, 오른쪽 가지는 5×5의 수용 영역을 가진다. 그렇게 하여 하나의 유닛을 통해 3×3과 5×5의 수용 영역을 가지는 국부적 특징값을 추출할 수 있다. 각각의 가지는 최종적으로 하나의 특징맵으로 연쇄(Concatenation)한다. 그리고 유닛의 층이 깊어질수록 학습할 때 기울기값이 사라지는 문제(Vanishing gradient)를 방지하기 위해 블록의 입력과 출력 사이에 곧바로 건너뛰는 연결선을 추가하였다.
3.3 잔여 학습
영상 잡음 제거의 목적은 다음과 같다.
| (1) |
(2)의 식에서 잡음이 있는 영상을 y, 깨끗한 영상을 x, 잡음을 v라고 했을 때, 잡음이 있는 영상 y에서 깨끗한 영상 x를 복원하는 것이다.
| (2) |
일반적으로 딥러닝 기반의 영상 잡음 제거 모델들은 식 (3)처럼 깨끗한 영상을 학습하는 것을 기반으로 한다.
| (3) |
하지만 제안된 모델에서는 최근 각광받고 있는 잔여 학습(Residual learning)을 통해 식 (4)처럼 잡음을 학습하도록 하였다. 잔여학습의 손실함수는 다음과 같다.
| (4) |
식 (5)에서 ni는 잡음을 의미하며, 잡음을 포함하는 영상 패치(Patch)에서 깨끗한 영상의 패치의 차 값이다.
논문 [14]에 따르면, 잡음이 포함된 영상에서 깨끗한 영상을 찾는 것보다 잡음을 찾는 것이 입력 영상으로부터 얻을 수 있는 고유의 정보와 더 가깝기 때문에 잔여 학습을 통한 딥러닝 기반의 영상 잡음 제거 모델이 더 효율적이다.
Ⅳ. 실험 결과
4.1 실험을 위한 세팅
열화상 영상 잡음 제거 모델 학습을 위해 자체 데이터셋을 사용하였다. 데이터셋은 640×480 해상도 비디오를 31Fps로 녹화하는 엘에스엘 시스템즈의 Argo-S 열화상 카메라를 이용하여 전남대학교 캠퍼스 내에서 촬영하였다. 전남대학교 캠퍼스에서 엣지(Edge)와 질감(Texture)를 포함할 수 있는 복잡한 환경을 가지는 강의실과 연구실을 대상으로 학습용 데이터를 촬영하였고, 실제 Argo-S 열화상 카메라에서 생기는 잡음을 촬영하기 위해서 온도가 2℃ 미만인 밀폐된 공간에서 데이터를 수집하였다.
열화상 영상 잡음 제거 모델 학습의 데이터 증강을 위해 영상에서 40×40 크기의 작은 패치를 14픽셀 간격을 두어 사용하였다. 얻어진 패치는 반전, 크기 변환, 회전을 사용하여 다시 한 번 데이터 증강을 적용하여 최종적으로 학습에 사용한 이미지는 1,044,548장이다.
Experimental environment setting, (a) Environment of taking a video with thermal camera, (b) Argo-S thermal camera by LSL systems company
딥러닝 학습은 Python기반 TensorFlow로 모델을 구현하였으며, 학습 개발 환경은 Nvidia Tesla K40c GPU를 사용하였다.
제안된 모델의 성능과 처리속도를 비교하기 위하여 고전적인 방법부터 최신의 영상 잡음 제거 방법까지 자체 데이터셋을 활용하여 테스트하였다. 테스트 환경은 Intel(R) Core(TM) i7-4790 CPU 3.60Hz, 8GB 램 환경에서 실시했고 그 결과는 그림 6에서 확인할 수 있다.
4.2 실험 평가
이 장에서는 기존의 영상 잡음 제거 방법에서부터 최신의 방법과 제안하는 모델과의 실험을 다양한 잡음과 환경에서 보여줄 것이다.
표 1은 제안하는 방법과 다른 최신의 방법들과의 라플라스 잡음에 대한 테스트에서 신호 대 잡음비(PSNR) 비교 결과를 보여준다. 스케일 값이 커질수록 잡음의 정도가 심해진다. 실험에서 각각의 라플라스 스케일 수준에 따른 잡음 분포가 섞인 영상을 입력으로 받아 해당하는 라플라스 스케일 값에 따른 학습 모델을 선택하여 최종 신호 대 잡음비를 산출하였다. 다른 최신의 영상 잡음 제거 방법들은 가우시안 잡음 분포의 표준편차 값을 라플라스 잡음 분포 스케일 값에 대응되도록 변경하여 실험하였다.
Average PSNR(dB) of Laplace noise
표 1에서 라플라스 잡음 분포 스케일 값은 4가지로 분류하였으며, 스케일 값이 점점 커지도록 구성하였다. 표 2에서 가우시안 잡음 분포 표준편차 값도 4가지로 분류하였으며, 표준편차 값이 점점 커지도록 구성하였다.
Average PSNR(dB) of Gaussian noise
표 1에서 제안한 방법은 최신의 다른 영상 잡음 제거 방법들과 비교하였을 때 모든 라플라스 잡음 스케일에서 최고의 성능을 보였다. 특히 라플라스 잡음 스케일 값이 b = 5에서 최고의 영상 잡음 제거 44.31dB를 달성하였다. 라플라스 잡음 분포 스케일 값이 커질수록 신호 대 잡음비 값이 줄어드는 것을 알 수 있다. 라플라스 잡음 분포가 섞인 이미지의 잡음 제거한 결과는 그림 5에서 확인할 수 있다.
Denoising results with Laplace noise
표 2는 제안하는 방법과 다른 최신의 방법들과의 가우시안 잡음에 대한 테스트에서 신호 대 잡음비 비교 결과를 보여준다. 표준편차 값이 커질수록 잡음의 정도가 심해진다. 실험에서 각각의 가우시안 표준편차 수준에 따른 잡음 분포가 섞인 영상을 입력으로 받아 해당하는 가우시안 표준편차 값에 따른 학습 모델을 선택하여 최종 신호 대 잡음비를 산출하였다. 다른 최신의 영상 잡음 제거 방법들도 가우시안 잡음 분포의 표준편차 값에 따른 모델을 선택하여 실험하였다. 표 2에서 가우시안 잡음 분포 표준편차 값은 4가지로 분류하였으며, 표준편차 값이 점점 커지도록 구성하였다. 이 실험이 제안하는 방법과 다른 최신의 방법들과 비교하는 실질적인 실험이다.
표 2에서 제안한 방법은 최신의 다른 영상 잡음 제거 방법들과 비교하였을 때 모든 가우시안 잡음 표준편차 값에서 최고의 성능을 보였다. 특히 가우시안 잡음 스케일 값이 σ = 10에서 최고의 영상 잡음 제거 42.74dB를 달성하였다. 가우시안 잡음 분포 표준편차 값이 커질수록 신호 대 잡음비 값이 줄어드는 것을 확인할 수 있다. 가우시안 잡음 분포가 섞인 이미지의 잡음 제거한 결과는 그림 6에서 확인할 수 있다.
Denoising results with Gaussian noise
표 3은 제안하는 방법의 학습된 모델에 따라 다양한 잡음에 대한 테스트에서 신호 대 잡음비 비교 결과를 보여준다. 열화상 영상에서의 잡음 제거 외에 일반적인 영상에서의 잡음 제거 효과를 확인해보기 위한 실험이다. 실험은 라플라스 잡음 분포 실험과 가우시안 잡음 분포 실험에서 최고의 신호 대 잡음비 결과를 보인 모델을 채택하여 각각 가우시안 잡음, 라플라스 잡음, 포아송 잡음, 간섭 잡음, 소금&후추 잡음이 섞인 영상을 테스트 하였다. 표 3에는 최종 결과만 보여주지만, 포아송 잡음은 특별한 실험 결과 패턴을 보였기 때문에 추가적으로 포아송 잡음을 학습한 모델을 추가하여 실험을 진행하였다.
Average PSNR(dB) based on proposed model of denoising results with various noises
라플라스 잡음을 학습한 모델은 포아송 잡음을 제외한 다른 잡음에 대하여 비교적 강인한 영상 잡음 제거 성능을 보였다. 가우시안 잡음을 학습한 모델은 라플라스 잡음을 학습한 모델보다 성능이 떨어졌지만 간섭(Speckle) 잡음에 대해서는 강인한 영상 잡음 제거 성능을 보였다. 포아송 잡음은 다른 잡음과 다른 실험 결과 패턴을 보여 포아송 잡음을 학습한 모델에서만 강인한 영상 잡음 제거 성능을 보였다. 표 3의 실험 결과를 기반으로 라플라스 잡음 모델 기반의 제안하는 영상 잡음 제거 방법은 열화상 영상 잡음 제거뿐만 아니라 일반적인 영상 잡음 제거에도 효과가 있음을 증명할 수 있다. 이와 관련된 결과는 그림 7에서 확인할 수 있다.
Denoising results with test images by each model based on Laplace, Gaussian and Poisson noise
제안하는 방법을 학습할 때, 전체 구조에서 반복가능한 인셉션-레지듀얼 블록의 수를 다르게 하여 학습하였다. 표 4는 블록을 2개부터 2배씩 증가하여, 2개 블록, 4개 블록, 8개 블록 그리고 16개 블록으로 학습한 모델을 검증한 것이다.
Average PSNR(dB) and time according to number of blocks
표 4에서 블록 수를 늘릴수록 신호 대 잡음비 성능이 향상되지만, 그만큼 소요 시간이 늘어난 것을 확인할 수 있다. 예를 들어 2개 블록에서 4개 블록으로 늘리면 모델의 신호 대 잡음비 성능은 0.63dB 향상되지만, 시간은 0.5308초 늘어난다.
그리고 블록 수를 더 많이 늘리면 늘릴수록 영상 잡음 제거 성능은 높아지고, 연산량은 늘어난다. 이와 같은 상관관계를 고려하여 본 논문에서는 2개의 블록으로 학습한 모델 기반의 방법을 제안하여 영상 잡음 제거 성능과 함께 빠른 처리 시간을 취할 수 있도록 한다.
본 논문에서는 2개의 인셉션-레지듀얼 블록으로 구성된 영상 잡음 제거 방법을 Nvidia Tesla K40c GPU에서 학습하였고, 테스트는 Intel(R) Core(TM) i7-4790 CPU 3.60Hz과 8GB 램에서 진행하였다. CPU 환경에서 제안하는 방법과 최신의 다른 영상 잡음 제거 방법과의 성능 및 처리 속도 비교를 진행한 결과는 표 5에서 확인할 수 있다.
Comparison of processing time with PSNR
표 5에서 제안하는 방법은 가장 성능이 좋은 DnCNN[14] 모델과 비교하였을 때 신호 대 잡음비의 결과가 더 좋으며 처리 속도가 약 2배 정도 더 빠른 것을 확인할 수 있다. WNNM[10]은 영상 잡음 제거를 할 수 있긴 하지만 한 장의 영상을 처리하는 시간이 너무 많이 소요되어 실제 응용에서는 사용할 수 없다.
따라서 본 논문에서 제안하는 반복가능한 인셉션-레지듀얼 블록의 수를 적절히 조절하면 높은 성능뿐만 아니라 처리 시간도 효율적으로 확보할 수 있는 영상 잡음 제거 모델이 가능하다.
그림 8은 열화상 카메라에서 발생하는 잡음에 대해서 다양한 영상 제거 방법을 적용한 결과이다. 파란색과 주황색 박스는 질감과 엣지를 살펴보기 위해 확대한 영역이다. 제안하는 방법은 처리 속도가 빠르며 가장 좋은 성능을 보여준다.
Denoising results with original thermal noise
V. 결 론
열화상 카메라에 따라 다르긴 하지만, 최소 온도와 최대 온도 사이가 극히 작은 차이일 때, 열화상 영상은 샘플링과 양자화로 인해 잡음이 발생한다. 이 때 발생하는 영상 잡음은 라플라스 잡음 분포와 유사하고, 이를 제거하기 위해 딥러닝 기반의 영상 잡음을 위한 인셉션-레지듀얼 블록을 포함하는 모델을 제안하였다. 제안된 모델은 잔여 학습을 통해 라플라스 잡음 및 다양한 잡음을 학습시켜 열화상 잡음 영상 및 다양한 영상 잡음에 적용하였으며, 특히 인셉션-레지듀얼 블록은 열화상 영상 잡음에 최적화된 필터를 포함하여 수용 영역 및 연산량 최소화에 도움을 준다.
제안된 모델은 자체 열화상 영상 데이터셋을 활용하여 실험하여 다양한 스케일의 라플라스 잡음에 대하여 평균 72.5%의 잡음 개선도를 보였고, 기존의 가장 좋은 성능을 보인 DnCNN[14]과 결과를 비교해도 평균 1.29dB의 PSNR 개선을 보였다.
제안된 모델에서 인셉션-레지듀얼 블록의 수를 증가시킬수록 영상 잡음 제거 성능이 향상되지만 처리속도 역시 증가하는 것을 확인할 수 있었다. 적절한 영상 잡음 개선과 처리속도의 상관관계를 고려하여 모델을 구성한다면 원하는 임무에 맞게 최고의 성능을 발휘할 수 있는 변형 가능한 모델이 될 수 있을 것이다.
Acknowledgments
"본 연구는 과학기술정보통신부 및 정보통신기획평가원의 대학ICT연구센터지원사업의 연구결과로 수행되었음" (IITP-2019-2016-0-00314)
References
-
M. Lindenbaum, M. Fischer, and A. Bruckstein. "On gabor contribution to image enhancement", Pattern Recognition, Vol. 27, No. 1, pp. 1-8, Jan. 1994.
[https://doi.org/10.1016/0031-3203(94)90013-2]
-
L. Alvarez, P. L. Lions, and J. M. Morel, "Image selective smoothing and edge detection by nonlinear diffusion (ii)", SIAM Journal of numerical analysis, Vol. 29, No. 3, pp. 845-866, Jun. 1992.
[https://doi.org/10.1137/0729052]
-
P. Perona and J. Malik, "Scale space and edge detection using anisotropic diffusion", IEEE Trans. Patt. Anal .Mach. Intell, Vol. 12, No. 7, pp. 629-639, Jul. 1990.
[https://doi.org/10.1109/34.56205]
-
L. Rudin, S. Osher, and E. Fatemi, "Nonlinear total variation based noise removal algorithms", Physica D: Nonlinear Phenomena, Vol. 60 No. 1-4, pp. 259-268, Nov. 1992.
[https://doi.org/10.1016/0167-2789(92)90242-F]
-
R. Coifman and D. L. Donoho, "Translation invariant denoising", in Wavelets and Statistics. New York: Springer-Verlag, Lecture Notes in Statistics, 103, pp. 120-150, 1995.
[https://doi.org/10.1007/978-1-4612-2544-7_9]
-
D. L. Donoho, "De-noising by soft-thresholding", IEEE Transactions on Information Theory, Vol. 41, No. 3, pp. 613-627, May 1995.
[https://doi.org/10.1109/18.382009]
-
K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, "Image denoising by sparse 3-D transform-domain collaborative filtering", IEEE Transactions on Image Processing, Vol. 16, No. 8, pp. 2080-2095, Aug. 2007.
[https://doi.org/10.1109/TIP.2007.901238]
-
J. Mairal, F. Bach, J. Ponce, G. Sapiro, and A. Zisserman, "Non-local sparse models for image restoration", in IEEE International Conference on Computer Vision, Kyoto, Japan, pp. 2272-2279, Oct. 2009.
[https://doi.org/10.1109/ICCV.2009.5459452]
-
W. Dong, L. Zhang, G. Shi, and X. Li, "Nonlocally centralized sparse representation for image restoration", IEEE Transactions on Image Processing, Vol. 22, No. 4, pp. 1620-1630, Apr. 2013.
[https://doi.org/10.1109/TIP.2012.2235847]
- S. Gu, L. Zhang, W. Zuo, and X. Feng, "Weighted nuclear norm minimization with application to image denoising", in IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, pp. 2862-2869, 2014.
-
H. C. Burger, C. J. Schuler, and S. Harmeling, "Image denoising: Can plain neural networks compete with BM3D?", in IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, pp. 2392-2399, Jun. 2012.
[https://doi.org/10.1109/CVPR.2012.6247952]
-
U. Schmidt and S. Roth, "Shrinkage fields for effective image restoration", in Proc. of Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, pp. 2774-2781, Jun. 2014.
[https://doi.org/10.1109/CVPR.2014.349]
-
Y. Chen and T. Pock, "Trainable nonlinear reaction diffusion: A flexible framework for fast and effective image restoration", IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 36, No. 6, pp. 1256-1272, Jun. 2017.
[https://doi.org/10.1109/TPAMI.2016.2596743]
-
K. Zhang, W. Zuo, Y. Chen, D. Meng, and L. Zhang, "Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising", in IEEE Transactions on Image Processing, Vol. 26, No. 7, pp. 3142-3155, Jul. 2017.
[https://doi.org/10.1109/TIP.2017.2662206]
- C. Szegedy, S. Ioffe, and V. Vanhoucke, "Inception-v4, inception-resnet and the impact of residual connections on learning", Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), San Francisco, California, USA, pp. 4278-4284, Feb. 2017.
- B. Ahn and N. I. Cho, "Block-Matching Convolutional Neural Network for Image Denoising", Computer Vision and Pattern Recognition (cs.CV), arXiv:1704.00524, , Apr. 2017.
-
Kai Zhang, Wangmeng Zuo, and Lei Zhang, "FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising", IEEE Transactions on Image Processing, Vol. 27, No. 9, pp. 4608-4622, Sep. 2018.
[https://doi.org/10.1109/TIP.2018.2839891]
- Kai Zhang, Wangmeng Zuo, and Lei Zhang, "Learning a single convolutional super resolution network for multiple degradations", In IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, Jun. 2018.
- Jin-Woo Kim and Phill-Kyu Rhee, "Image Recognition based on Adaptive Deep Learning", Journal of IIBC, Vol. 18, No. 1, pp. 113-117, Feb. 2018.
- Kyung Min Lee and Chi Ho Lin, "Video Stabilization Algorithm of Shaking image using Deep Learning", Journal of IIBC, Vol. 19, No. 1, pp. 145-152, Feb. 2019.
2018년 2월 : 전남대학교 전자컴퓨터공학과(공학석사)
2018년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과(박사과정)
2018년 12월 ~ 현재 : 인섹피디아 회사 창업
관심분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신러닝, 딥러닝
2017년 2월 : 전남대학교 전자컴퓨터공학과(공학사)
2019년 2월 : 전남대학교 전자컴퓨터공학과(공학석사)
2019년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과(박사과정)
관심분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신러닝
2017년 9월 : 베트남 호치민 과학대학교 수학, 컴퓨터과학과(공학사)
2018년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과(석사과정)
관심분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신러닝
2018년 9월 : 베트남 호치민 과학대학교 수학, 컴퓨터과학과(공학사)
2019년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과(석박사통합과정)
관심분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신 러닝
2012년 9월 : 베트남 타이녁 기술 대학교 전자공학과(공학사)
2015년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과(석박사통합 과정)
관심분야 : 컴퓨터 비전, 웨어러블 장치, 시스템 기반의 마이크로프로세서, 머신러닝, 딥러닝
2017년 11월 : 더뉴어 회사 창업
2019년 8월 : 전남대학교 지구환경 과학부(이학사)
2019년 9월 ~ 현재 : 전남대학교 전자컴퓨터공학과(석사과정)
관심분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신러닝
1993년 2월 : 동신대학교 정보공학과(공학사)
1998년 2월 : 전남대학교 전자공학과(공학석사)
2017년 2월 : 전남대학교 전자정보공학과(공학박사)
2019년 8월 ~ 현재 : 전남대학교 전자컴퓨터공학과(박사후연구원)
관심분야 : 디지털 신호처리, 영상 처리, 바이오매트릭스
1986년 2월 : 서울대학교 전자공학과(공학사)
1988년 2월 : 서울대학교 전자공학과(공학석사)
1994년 8월 : 서울대학교 전자공학과(공학박사)
1995년 3월 ~ 현재 : 전남대학교 전자컴퓨터공학과 교수
관심 분야 : 디지털 신호처리, 영상 처리, 음성 신호처리, 머신러닝, 딥러닝