Pavement Crack Detection and Segmentation Based on Deep Neural Network
Abstract
Cracks on pavement surfaces are critical signs and symptoms of the degradation of pavement structures. Image-based pavement crack detection is a challenging problem due to the intensity inhomogeneity, topology complexity, low contrast, and noisy texture background. In this paper, we address the problem of pavement crack detection and segmentation at pixel-level based on a Deep Neural Network (DNN) using gray-scale images. We propose a novel DNN architecture which contains a modified U-net network and a high-level features network. An important contribution of this work is the combination of these networks afforded through the fusion layer. To the best of our knowledge, this is the first paper introducing this combination for pavement crack segmentation and detection problem. The system performance of crack detection and segmentation is enhanced dramatically by using our novel architecture. We thoroughly implement and evaluate our proposed system on two open data sets: the Crack Forest Dataset (CFD) and the AigleRN dataset. Experimental results demonstrate that our system outperforms eight state-of-the-art methods on the same data sets.
초록
도로 포장면의 크랙(crack)은 도로포장 구조의 열화를 입증하는 중요한 신호와 증상이다. 카메라 영상기반 도로포장 크랙 탐지는 강도 비균질성, 위상 복잡성, 낮은 대조도 및 노이즈성의 텍스처 배경 때문에 어려운 문제이다. 본 논문은 흑백영상에 대하여 깊은 신경망(DNN)에 기반하여 픽셀수준의 도로 크랙 탐지 및 분할 문제에 대해 다룬다. 변형된 U-net 네트워크와 고수준 특징 네트워크를 포함하는 새로운 DNN 구조를 제안한다. 본 연구의 중요 기여는 융합 층을 통해 공급되는 이들 네트워크의 결합 방법이다. 우리가 아는 한, 본 연구는 보도블럭 크랙 분할 및 탐지 문제를 결합을 소개한 최초의 논문이다. 크랙 탐지 및 분할의 시스템 성능은 새로운 구조를 사용하여 급격히 향상되었다. 제안된 시스템을 2개의 공개 데이터셋크랙 포레스트 데이터셋(CFD)와 AigleRN 데이터셋에 대하여 구현하고 평가하였다. 본 논문의 시스템은 여덟 가지의 최신 알고리즘과 같은 데이터셋으로 실험을 하였을 때, 가장 뛰어난 결과를 보여주었다.
Keywords:
pavement crack detection, deep learning, crack segmentationⅠ. Introduction
The detection and segmentation of cracks on a pavement surface are the important tasks in a pavement maintenance system. The traditional manual inspection method is time-consuming, labor-insensitive, and potentially hazardous for both inspectors and road users. Moreover, manual inspection completely depends on the individual specialists experience and knowledge, which lead to low objectivity in quantitative analysis [1]. For these reasons, image processing based techniques for crack detection have attracted significant attention in computer vision and other research communities. In this work, we focus on developing a new approach to automatically detect and segment cracks from gray-scale images.
Various crack detection methods have been suggested based on image processing. These methods can be classified into three categories, namely: conventional methods, current methods, and deep learning-based methods. The conventional methods basically attempted to find suitable thresholds to isolate cracks from input images.
However, these methods did not result in good detection due to numerous crack shapes, different sizes, and various noises such as shading and intensity inhomogeneity. In order to overcome these problems, many recent techniques, such as the minimal path-Based techniques, have been proposed to detect cracks based on the assumption that cracks appear darker than surrounding contexts. In general, machine learning based methods have been introduced to classify cracks on input images based on nominated features. The major disadvantage of machine learning-based methods is that the system performance relies on features and parameters which are usually difficult to select. Recently, deep learning-based approaches have achieved significant performances in detection, classification, and segmentation problems without any assumption of data distribution. Deep neural networks are able to learn and adjust trainable parameters based on numerous of training data samples. Therefore, millions of data points are necessary to train a deep neural network. More specifically, deep learning methods have been successfully applied on pixel-wise detection and segmentation tasks for medical applications [2][3]. In addition, U-shaped networks [2][4] have shown good performance with fewer trainable parameters than other traditional convolution neural network (CNN) based methods for segmentation tasks.
In this paper, we address the problems of crack detection and segmentation on gray-scale images with a small number of training images using a deep learning method based on an end-to-end training approach. Our approach is inspired by the well-known U-net network [2]. The original U-net network structure includes millions number of trainable parameters which is not suitable for practical applications. Therefore, a modified version of the U-net network is introduced in this paper including the encoder and decoder branches called the modified U-net network, which contains a small number of learning parameters.
In addition, we figure out that the modified U-net network cannot guarantee the system robustness, especially in the case of cracks which have small sizes. In order to overcome these limitations, a high-level features network is proposed to learn deeper features from input images independently in another branch. A fusion layer is applied to merge matrix features from the encoder branch of the modified U-net network with the High-level features Network. This combination dramatically improves system performance with a small amount of training data and a small number of learning parameters.
In the rest of this paper, we review the related works in Section II. In Section III, the proposed method and network architecture are discussed in detail. Two open data sets and experimental results are given in Section IV. Finally, Section V concludes this paper.
Ⅱ. Related works
The problems of crack detection and segmentation can be considered to be the first step of pavement evaluation and maintenance systems, where the purpose is to distinguish cracks from other areas on pavement surfaces. Crack detection problems are naturally challenging due to the inhomogeneity of intensity, low-contrast, shadows, and cracks’ complexity.
In early works, crack detection and segmentation problems were addressed using conventional edge detector algorithms. Zhao et al. proposed an improved Canny edge detection algorithm for pavement edge detection applications [5]. They mainly used Mallat wavelet transform to strengthen the weak edges of input images and set the proper threshold based on the quadratic optimization of a genetic algorithm. Threshold-based approaches were applied due to their simplicity and low computation time. Oliveira and Correia [6] proposed the use of entropy and dynamic threshold methods to automatically segment cracks from input images. First, they applied morphology filters to reduce the variance of pixel values. A dynamic threshold was adopted to extract dark pixels which were considered to be crack candidates. After dividing threshold image into non-overlapping blocks, they computed entropy and applied another dynamic threshold in order to obtain final crack results. A fast crack detection method based on percolation image processing for a large-size concrete surface image was introduced in [7]. The termination- and skip-added procedures were proposed to reduce the computation cost. A Local Binary Pattern was introduced in [8] to detect cracks, whereby local neighbors were first classified into smooth areas and rough areas. The local pattern was applied on the rough area in order to obtain structure information. The Laplacian of Gaussian algorithm was presented for detecting cracks on road surfaces [9][10]. Generally, these conventional methods are sensitive to noise, which leads to unreliable results in poor lighting conditions.
More recently, Minimal Path-Based techniques were widely applied to detect cracks from images. In these techniques, an image was considered to be a graph of pixels weighted by pixel intensities. A minimal path was defined as the path in which the sum of pixel intensities was the smallest value. Nguyen et al. introduced a method of calculating features along every free-form path which was able to detect cracks with any form and any orientation [11] namely Free-Form Anisotropy (FFA). A dynamic programming implementation of the FFA approach was presented by Avila et al. in [12]. Amhaz et al. presented a Minimal Path Selection (MPS) approach where the end points of a crack were selected from a local scale and the minimal part of the crack was selected from a global scale [13][14]. Another more general method was presented by Kaul et al. in [15], in which complex curves were estimated without knowledge of either the endpoints or the topologies of curves. Their algorithm required only one arbitrary initial point to detect the complete curve. A fully-automatic method was also proposed [16].
They developed a geodesic shadow-removal algorithm to remove pavement shadows from input images and generated probability maps based on a tensor voting algorithm. A set of crack seeds was sampled from a crack probability map. Finally, minimum spanning trees were used to extract the final crack curves. A multiple-scale fusion crack detection (MFCD) approach based on the minimal intensity path was introduced by Li et al. [17]. The authors estimated the crack candidates at each scale and evaluated them based on several statistical hypotheses. The main disadvantage of minimal path-based method is that the computation cost is too high for real-time application.
In additional, a numerous of approaches relied on machine learning algorithms to classify crack and non-crack images or detect the cracks’ positions from input images were proposed. A fully automatic crack detection system was proposed called CrackIT [18][19], where different classification strategies were applied to classify the cracks on non-overlapping image blocks. Cord et al. proposed an approach using texture patterns based on AdaBoost classifier. In addition, the Support Vector Machine (SVM) classifier was applied to classify crack and non-crack images based on texture and shape descriptors [20] and graph-based features [21]. The Support Vector Machine-based method was applied in order to compute probability maps using information on multi-scale neighborhoods; this was called a Probabilistic Generative Model - Support Vector Machine (PGM-SVM) [22]. In addition, the Random Structure Forest-based method demonstrated good performance as well [23]. However, features extraction and selection steps, which are challenging tasks, are necessary to applied machine learning-based approaches.
In recent years, deep learning has demonstrated significant performance enhancements in image classification, detection, and segmentation tasks [24]. Zhang et al. proposed the ConvNets method [25], which included four convolution layers, four max-pooling layers, and two fully connected layers, to classify an individual pixel in terms of whether or not it belonged to a crack, based on local patch information. A combination between CNNs and the sliding window technique for detecting cracks was proposed in [26]. A neural network classifier trained on ImageNet pre-trained VGG-16 DCNN features was proposed in order to distinguish between crack images and non-crack images [27]. Fan et al. [28] addressed the problem of automatic crack detection based on a structured prediction with CNN. On the other hand, CNN was applied to calculate the mean texture depth (MTD) of a crack without computing the surface texture features statistics [29]. The proposed network included only one convolution layer, one pooling, and one fully connected layer.
However, thousands to millions of images are necessary for training the network. Zhang et al. proposed CrackNet [30] to detect cracks on 3D asphalt surfaces with four layers and included more than one million parameters that were trained in the learning process. A recurrent neural network (RNN) version called CrackNet-R was proposed in [31] for fully automated pixel-level crack detection on three-dimensional (3D) asphalt pavement surfaces. An end-to-end style processing approach was proposed in [32] called a fully convolutional network (FCN). The down-sampling branch was from the famous VGG19 networks [33], and the up-sampling branch was implemented by adding specific layers from convolutional layers and deconvolution layers. Due to the use of VGG19, the number of learning parameters was up to millions, which much more than in our proposed approach. In general, the aforementioned deep learning-based methods required substantial amounts of input data images, and the learning time was extensive due to the excessive number of parameters that need to be learned.
In order to overcome these weaknesses, we propose a new network architecture for crack detection and segmentation at the pixel-level. The parameters in the proposed method are trained as an end-to-end style with only one input channel. The outputs of high-level features and low-level features, which were extracted independently, were fused so as to enhance the system performance. Moreover, our proposed network architecture can be considered a lightweight network, since the number of parameters trained during the learning task is around 500,000 parameters. We carefully tested and compared our proposed network architectures with other methods, including recent methods and other deep learning-based methods, on the same data sets.
Ⅲ. Methodology
Our approach mainly involves three steps. First, the input image is converted to gray-scale and pre-processed so as to reduce the effects of noise before being the input of the proposed network. The min-max normalization, histogram equalization, and Gama correction methods are adopted for the preprocessing task. Second, we employ a self-design network in order to learn the crack features from the input image. The proposed deep neural network includes two different feature extraction branches based on a convolution neural network with a small number of trainable parameters. In detail, the modified U-net network is introduced in the first subbranch. On the other hand, we propose an additional branch network to extract high level features. The learning features from the encoder branch and high-level features network are independent. The fusion layer allows us to merge the low-level features from our modified U-net network with the high-level features for further processing based on sharing parameters. The entire system is trained in an end-to-end fashion. The output of the system is the probability segmentation map.
Finally, we simply apply a threshold in order to obtain the binary output map. With a small amount of training data, our method achieves impressive detection results. A schematic overview of all of the processing steps is depicted in Fig. 1. The following subsections discuss these aforementioned steps in details.
3.1 Data preprocessing
Generally, in case of developing a deep network with high accuracy in a various situations, such as different levels of illumination or different shapes, we need to collect and label a large amount of data sets. Unfortunately, this is time-consuming and has a high cost. In order to address this problem, we apply simple and conventional preprocessing algorithms on the input image prior to training so as to reduce the effect of noise and enhance the system performance.
In detail, the input image is converted to gray-scale and normalized by min-max normalization to increase the contrast of the gray-scale image. The normalization image is generated by the following equation.
| (1) |
where I is the input image, Imin and Imax are the minimum and maximum pixel value of input image I, respectively, and Inor is the normalized image.
Then, the Contrast Limited Adaptive Histogram Equalization (CLAHE) method is applied in order to improve the contrast of the input image by adaptive histogram equalization [34].
Finally, Gamma correction is applied as the following equation to correct the image’s luminance.
| (2) |
where I is the input image of Gamma correction, γ is the correction parameter, and Iprocessed is the pre-processed image.
3.2 Network architecture
The proposed network architecture is inspired by the U-shaped structure networks. A modified version of U-net network is firstly introduced. In additional, we proposed a high-level feature network in order to learn deeper features separately.
The fusion layer is then adopted to combine the low-level features and high-level features. These modifications in the network architecture boost the system performance by a surprising amount. We separate the network architecture into two main networks: the modified U-net network and the high-level features network, as shown in Fig. 2.
The first part of the network architecture is based on the U-net architecture called the modified U-net network. It starts with a down-sampling (encoding) subbranch including four states. Each state includes two 3×3 convolution layers followed by a rectified linear unit (ReLU) [35] activation function, which has computational efficiency and is suitable for deep networks. Compared with the original U-net, we propose the use of zero-padding to retain the image shape after convolution layers. Moreover, Batch Normalization [36][37] is also adopted after each convolution layer in order to prevent an internal covariant shift as well as to ensure faster training convergence. A dropout layer [38] is applied between the convolution layers in the same state so as to prevent over-fitting of the system and improve the generalization of the network architecture. The dropout ratio is set to 0.2 after several experiments. Similar to U-net, the 2×2 max-pooling layer halves the resolution of the input matrix at the end of each stage, except for the last state. The number of filters in each layer is selected after several attempts, and the selected filter sizes are turnings of 4, 8, 16, and 32, as depicted in Fig. 2. In the deepest stage, the output layer matrix is merged with a high-level features network.
The up-sampling branch is based on a 3x3 de-convolution layer and convolution with ReLU, as well as zero-padding to recover the original size of input image. The architecture includes a contracting path to capture the context and a symmetric expanding path, as stated from the original U-net. Batch normalization and dropout layers are also applied on the up-sampling branch. However, the number of filters is decreased as follows: 32, 16, eight, and four. Finally, at the end of the network, the 1x1 convolution layer is adopted in order to obtain the final probability map.
As aforementioned, the high-level feature network is proposed to extract deeper features and work independently with the modified U-net network. A very deep convolutional network for image recognition was proposed in [33]. While this approach is well-known, the number of trainable parameters was relatively high due to the increased number of filters. We propose using a network called the high-level features network with only four stages of 3×3 convolution layers with ReLU, zero-padding, and 2×2 max-pooling layers, as presented in Fig. 2.
In the first two stages, we use two convolution layers in each stage, with the number of filters being 16, 16 and 32, 32, respectively. In contrast, in the last two stages, we apply three convolution layers in each stage with the filter sizes of 64, 64, 64, 128, 128, and 128, respectively. At the end of each stage, a 2×2 max-pooling layer is applied so as to reduce the sizes of the feature maps. We apply Batch-normalization immediately following each convolution layer. In the final stage, the feature map is merged with the feature maps from the encoder branch of the modified U-net network by the fusion layer. None of the layers used in our proposed architecture are fully connected.
3.3 Data post processing
The output or the network is the probability map which has value in range [0, 1]. The final binary output is created by using threshold value α as shown in the following equation.
| (3) |
where Ioutput is the final binary output image, α is the threshold value and Iprobability is the probability map which is the output from the trained network.
Ⅳ. Experiments
4.1 Dataset
Two open datasets are selected to evaluate our proposed approach. The Crack Forest Dataset (CFD) includes 118 RGB images with a resolution of 320x480 pixels [23]. These data are images of pavements in Beijing, China that were captured on an iPhone 5. All of the images are converted to gray-scale prior to further processing. In addition, the AigleRN dataset contains 38 gray-scale images. These images are gathered from France with a resolution of 311×462 pixels and 991×462 pixels and have been pre-processed in order to reduce illumination effects. For the first two experiments, we trained the network on two datasets independently. In the first experiment on the CFD dataset, we randomly select 83 images (70%) for training and 35 images (30%) for testing. In the second experiment on the AigleRN dataset, we randomly choose 27 images (70%) for training and 11 images (30%) for testing. Finally, we also investigate the network performance with cross data by using the CFD dataset for training and the AigleRN dataset for testing, and conversely.
4.1 Experimental setup
Our proposed method is implemented with the Google TensorFlow Keras Library, OpenCV Python and trained on a workstation with Intel Xeon E5-1620 3.60GHz CPU, 16GB RAM, and Nvidia Tesla K40 GPU.
In pre-processing step, we chose a small region size of 8×8 and the contrast limiting of 2.0 for the CLAHE algorithm. We select γ=0.67 for the Gamma correction method. These methods are executed by OpenCV Python. The network is trained on sub-images (patches). We randomly select 200,000 samples from the training dataset with a patch size of 40x40 for training our network. The training dataset is divided into 180,000 samples for training and 20,000 for validation. The training is performed for 100 epochs with a mini-batch size of 32 patches; the training time is almost 14 hours. Training the deep neural networks require stochastic gradient-based optimization in order to minimize cost function.
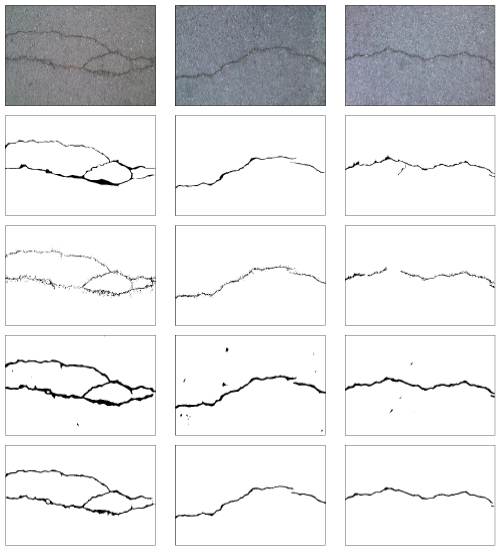
In testing phase, the crack probability of each pixel is generated by averaging the multiple prediction with overlapping patches. Multiple consecutive overlapping patches are extracted in each testing image with a specific stride of 5. Then, the crack probability of each pixel is computed by averaging the probability of all predicted patches which cover the pixels. A darker pixel is considered to be more likely to be a crack pixel. Finally, the simple decision probability is adopted to generate the binary output images, as depicted in Fig. 3.
Crack prediction results by our proposed method (From top to bottom: original images, ground truth, probability map, binary output)
In order to confirm the effectiveness of our method, we compare it with eight state-of-the-art methods: FFA [11][12], CrackTree[16], CrackIT [18][19], MPS [13][14], CrackForest [23], MFCD [17], PMG-SVM [22], and CNN[28]. We present the performances of these networks according to precision (Pr), recall (Re), and F1-score (F1) metrics. These metrics are computed by true positive (TP), false negative (FN), and false positive (FP), as presented in Table 1.
It is difficult to acquire high quality of ground truth for real images due to the transitional area between crack and non-crack pixels. The tolerance margins for measuring the coincident between ground truth and detected cracks are accepted in the evaluation to be five pixels as in [17][23] and two pixels as in [14][22][28]. In this paper, we show performance in both cases for comparison.
4.2 Evaluation
The CFD data set is selected in this section to evaluate the performance of our proposed approach. The decision probability α is set at 0.7. The numerical comparisons of our proposed method with other state-of-the-art methods are shown in Table 2 and Table 3 with the tolerance margins of 5 pixels and 2 pixels, respectively. With a tolerance margin of five pixels, our proposed approach outperform five state-of-the-art methods with significantly enhanced performance from 89.90% to 95.67%, 89.47% to 93.38%, and 89.68% to 94.51% for precision, recall, and F1-score, respectively. These results confirm that the deep-learning-based approach achieved the highest performance.
Table 3 show a comparison between our approach and the other four methods, including the deep learning-based method [28]. This CNN network is based on a VGG-net structure [33], which includes convolution layers, max-pooling layers, and fully-connected layers. Our network structure take advantage of extract deep features by using deep-level features and the end-to-end training style of U-net shape to achieve the highest precision, which is computed based on the number of corrected pixels.
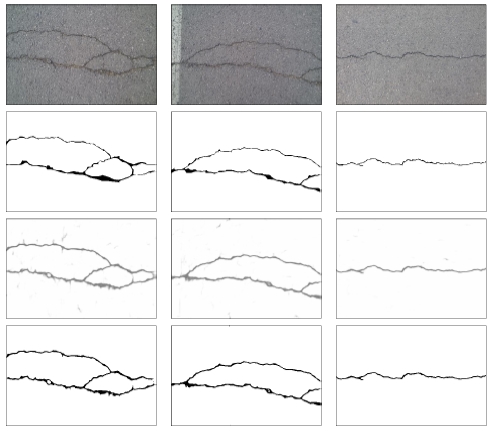
An illustration of the results obtaining by our proposed method and the other two latest methods including MFCD [17] and CNN-based method [28] is depicted in Fig. 4, as well as the original image and ground truth. While the MFCD method [17] fail to detect small cracks, we observe that the CNN-based method [28] extracted cracks with a wider crack width, which led to higher recall value. The effectiveness of our network architecture for segmentation tasks for thinner cracks is confirmed by observation.
Compared to CFD data set images, the AigleRN data set images have more complicated textures. We select the decision probability for the AigleRN dataset as 0.6. The overall performances are presented in Table 4 and Table 5 with tolerance margins of 5 pixels and 2 pixels, respectively. It is also observed that our proposed approach achieve better performance than all other approaches in all evaluation metrics. The Crack Forest [23] algorithm shows a good result compared to the other approaches. However, it is clear that deep learning-based approaches significantly enhance detection and segmentation performance. Furthermore, our proposed network architecture achieve better performance than the another approach based on CNN [28], as shown in Table 5.
The detection results of the different approaches on the AigleRN Dataset, including FFA [11][12], MPS [13][14], MFCD [17], CNN [28], and the proposed method are presented in Fig. 5 and Fig. 6. These figures demonstrate that the FFA [11][12] method is able to find some cracks that appear to be significantly different to the background, however it is unable to find the details of small cracks. While the MPS method is more effective in finding cracks from a global viewpoint, it can not extract full cracks due to the intensity changes. While the MPS method is more effective in finding cracks from a global viewpoint, it cannot extract full cracks due to the intensity changes.

Detection results on AigleRN dataset. from left to right: original images, ground truth images, FFA [11][12], MPS [13][14], MFCD [17], CNN [28], and our results

Detection results on AigleRN dataset. from top to bottom: original images, ground truth images, FFA [11, 12], MPS [13][14], MFCD [17], CNN [28], and our results
The CNN-based method [28] show good performance in terms of distinguishing the crack from the background; however, the CNN-based approach still has several false alarms. Our proposed method overcome these problems through a combination of high-level features networks (which consist of convolution layers and max-pooling layers) and the modified U-net network. This combination make our network architecture more effective in terms of learning deep features and retaining the geometric structure of the input image by the U-shape network.
This section describes the two experiments: i) training on CFD and testing on AigleRN, and ii) training on AigleRN and testing on CFD. We also provide experimental results with a tolerance margin of two pixels and five pixels in Table 4 and Table 5, respectively. The detection examples are depicted in Fig. 7. We observe that the predicted cracks on the AigleRN dataset by the trained mode on the CFD dataset are very thick due to the dataset characteristics. Weak cracks on the AigleRN dataset are overlooked, which decrease detection performance. Conversely, the predicted results on the trained model on the AigleRN dataset show that it is able to segment thin cracks, leading to high precision but low recall metrics. The detection examples are depicted in Fig. 7.
Ⅴ. Conclusions
An effective approach for automatic road crack detection at the pixel level based on a deep neural network was introduced in this paper. We propose a novel network architecture which combined the modified U-net network and the high-level features network using a fusion layer. The training is implemented in an end-to-end style. After applying conventional pre-processing algorithms, we train our network with a small number of input images. The proposed network architecture outperformed eight state-of-the-art methods on two published data sets. In terms of cross data generation, we observe that the trained models are affected by label data. The thinning of cracks in the training sample images led to degradation of the segmentation results. In fact, the ground truth label was made manually. Therefore, the system is able to achieve better performance in the case of a carefully labeled dataset. Based on these achievements, the proposed network architecture can be applied in further studies on different types of dataset, such as vessel segmentation, road segmentation from satellite images. In future, this work is able to use in embedded monitoring system for real applications such as road or bridge surface monitoring systems.
Acknowledgments
This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2019-2016-0-00314) supervised by the IITP
References
-
A. Mohan and S. Poobal, "Crack detection using image processing: A critical review and analysis", Alexandria Engineering Journal, Vol. 57, No. 2, pp. 787-798, Jun. 2018.
[https://doi.org/10.1016/j.aej.2017.01.020]

-
O. Ronneberger, P. Fischer, and T. Brox, "U-Nnet: Convolutional networks for biomedical image segmentation", Medical Image Computing and Computer-Assisted Intervention, MICCAI 2015, Springer, LNCS, Vol. 9351, pp. 234-241, May 2015.
[https://doi.org/10.1007/978-3-319-24574-4_28]

-
P. Liskowski and K. Krawiec, "Segmenting retinal blood vessels with deep neural networks", IEEE Trans Med. Imag., Vol. 35, No. 11, pp. 2369-2380, Nov. 2016.
[https://doi.org/10.1109/TMI.2016.2546227]

-
V. Badrinarayanan, A. Kendall, and R. Cipolla, "Segnet: A deep convolutional encoder-decoder architecture for image segmentation", IEEE Trans. Pattern Anal. Mach. Intell, Vol. 39, No. 12, pp. 2481-2495, Dec. 2017.
[https://doi.org/10.1109/TPAMI.2016.2644615]

-
H. Zhao, G. Qin, and X. Wang, "Improvement of canny algorithm based on pavement edge detection", Int. Congress on Image and Signal Processing, Vol. 2, pp. 964–967, Oct. 2010.
[https://doi.org/10.1109/CISP.2010.5646923]

- H. Oliveira and P. L. Correia, "Automatic road crack segmentation using entropy and image dynamic thresholding", European Signal Processing Conference, Glasgow, UK, pp. 622-626, Aug. 2009.
-
T. Yamaguchi and S. Hashimoto, "Fast crack detection method for large-size concrete surface images using percolation-based image processing", J. Machine Vision and Applications, Vol. 21, No. 5, pp. 797-809, Aug. 2010.
[https://doi.org/10.1007/s00138-009-0189-8]

-
Y. Hu and C. Zhao, "A novel LBP based methods for pavement crack detection", Journal of Pattern Recognition Research, Vol. 5, No. 1, pp. 140-147, Jan. 2010.
[https://doi.org/10.13176/11.167]

- R. S. Lim, H. M. La, Z. Shan, and W. Sheng, "Developing a crack inspection robot for bridge maintenance", IEEE Int. Conf. on Robotics and Automation, ICRA 2011, Shanghai, China, pp. 6288-6293, May 2011.
-
R. S. Lim, H. M. La, and W. Sheng, "A robotic crack inspection and mapping system for bridge deck maintenance", IEEE Trans. Autom. Sci. Eng., Vol. 11, No. 2, pp. 367-378, Apr. 2014.
[https://doi.org/10.1109/TASE.2013.2294687]

-
T. S. Nguyen, S. Begot, F. Duculty, and M. Avila, "Free-form anisotropy: A new method for crack detection on pavement surface images", IEEE Int. Conf. on Image Processing, ICIP 2011, Brussels, Belgium, pp. 1069-1072, Sep. 2011.
[https://doi.org/10.1109/ICIP.2011.6115610]

-
M. Avila, S. Begot, F. Duculty, and T.S. Nguyen, "2D image based road pavement crack detection by calculating minimal paths and dynamic programming", IEEE Int. Conf. on Image Processing, ICIP 2014, Paris, France, pp. 783-787, Oct. 2014.
[https://doi.org/10.1109/ICIP.2014.7025157]

-
R. Amhaz, S. Chambon, J. Idier, and V. Baltazart, "A new minimal path selection algorithm for automatic crack detection on pavement images", IEEE Int. Conf. on Image Processing, ICIP 2014, Paris, France, pp. 788-792, Oct. 2014.
[https://doi.org/10.1109/ICIP.2014.7025158]

-
R. Amhaz, S. Chambon, J. Idier, and V. Baltazart, "Automatic crack detection on two-dimensional pavement images: An algorithm based on minimal path selection", IEEE Trans. Intell. Transp. Syst., Vol. 17, No. 10, pp. 2718-2729, Oct. 2016.
[https://doi.org/10.1109/TITS.2015.2477675]

-
V. Kaul, A. Yezzi, and Y. Tsai, "Detecting curves with unknown endpoints and arbitrary topology using minimal paths", IEEE Trans. Pattern Anal. Mach. Intell, Vol. 34, No. 10, pp. 1952-1965, Oct. 2012.
[https://doi.org/10.1109/TPAMI.2011.267]

-
Q. Zou, Y. Cao, Q. Li, Q. Mao, and S. Wang, "Cracktree: Automatic crack detection from pavement images", Pattern Recognition Letters, Vol. 33, No. 3, pp. 227-238, Feb. 2012.
[https://doi.org/10.1016/j.patrec.2011.11.004]

-
H. Li, D. Song, Y. Liu, and B. Li, "Automatic pavement crack detection by multi-scale image fusion", IEEE Transactions on Intelligent Transportation Systems, Vol. 20, No. 6, pp. 2025-2036, Jun. 2019.
[https://doi.org/10.1109/TITS.2018.2856928]

-
H. Oliveira and P. L. Correia, "Automatic road crack detection and characterization", IEEE Trans. Intell. Transp. Syst., Vol. 14, No. 1, pp. 155-168, Mar. 2013.
[https://doi.org/10.1109/TITS.2012.2208630]

-
H. Oliveira and P. L. Correia, "CrackIT – an image processing toolbox for crack detection and characterization", IEEE Int. Conf. on Image Processing, ICIP 2014, Paris, France, pp. 798-802, Oct. 2014.
[https://doi.org/10.1109/ICIP.2014.7025160]

-
Y. Hu, C. Zhao, and H. Wang, "Automatic pavement crack detection using texture and shape descriptors", Int. J. IETE Technical Review, Vol. 27, No. 5, pp. 398-405, Sep. 2010.
[https://doi.org/10.4103/0256-4602.62225]

-
K. Fernandes and L. Ciobanu, "Pavement pathologies classification using graph-based features", IEEE Int. Conf. on Image Processing, ICIP 2014, Paris, France, pp. 793-797, Oct. 2014.
[https://doi.org/10.1109/ICIP.2014.7025159]

-
D. Ai, G. Jiang, L. Siew Kei, and C. Li, "Automatic pixellevel pavement crack detection using information of multi-scale neighborhoods", IEEE Access, Vol. 6, pp. 24452-24463, Apr. 2018.
[https://doi.org/10.1109/ACCESS.2018.2829347]

-
Y. Shi, L. Cui, Z. Qi, F. Meng, and Z. Chen, "Automatic road crack detection using random structured forests", IEEE Trans. Intell. Transp. Syst., Vol. 17, No. 12, pp. 3434–3445, Dec. 2016.
[https://doi.org/10.1109/TITS.2016.2552248]

- A. Krizhevsky, I. Sutskever, and G.E. Hinton, "ImageNet classification with deep convolutional neural networks", Int. Conf. on Neural Information Processing Systems, NIPS 2012, Vol. 1, pp. 1097-1105, Dec. 2012.
-
L. Zhang, F. Yang, Y. Daniel Zhang, and Y. J. Zhu, "Road crack detection using deep convolutional neural network", IEEE Int. Conf. on Image Processing, ICIP 2016, Phoenix, AZ, USA, pp. 3708-3712, Sep. 2016.
[https://doi.org/10.1109/ICIP.2016.7533052]

-
Y. J. Cha, W. Choi, and O. Buyukozturk, "Deep learning-based crack damage detection using convolutional neural networks", Computer-Aided Civil and Infrastructure Engineering, Vol. 32, No. 5, pp. 361-378, May 2017.
[https://doi.org/10.1111/mice.12263]

-
K. Gopalakrishnan, S. K. Khaitan, A. Choudhary, and A. Agrawal, "Deep convolutional neural networks with transfer learning for computer vision-based data-driven pavement distress detection", Int. J. Construction and Building Materials, Vol. 157, pp. 322-330, Dec. 2017.
[https://doi.org/10.1016/j.conbuildmat.2017.09.110]

- Z. Fan, Y. Wu, J. Lu, and W. Li, "Automatic pavement crack detection based on structured prediction with the convolutional neural network", CoRR, arXiv:1802.02208v1 [cs.CV] 1 Feb. 2018.
-
Z. Tong, J. Gao, A. Sha, L. Hu, and S. Li, "Convolutional neural network for asphalt pavement surface texture analysis", Computer-Aided Civil and Infrastructure Engineering, Vol. 33, No. 12, pp. 1056-1072, Dec. 2018.
[https://doi.org/10.1111/mice.12406]

-
A. Zhang, K. C. P. Wang, B. Li, E. Yang, X. Dai, Y. Peng, Y. Fei, Y. Liu, J. Q. Li, and C. Chen, "Automated pixel-level pavement crack detection on 3d asphalt surfaces using a deep-learning network", Computer-Aided Civil and Infrastructure Engineering, Vol. 32, No. 10, pp. 805-819, Oct. 2017.
[https://doi.org/10.1111/mice.12297]

-
A. Zhang, K. C. P. Wang, Y. Fei, Y. Liu, C. Chen, G. Yang, J. Q. Li, E. Yang, and S. Qiu, "Automated pixel-level pavement crack detection on 3D asphalt surfaces with a recurrent neural network", Computer-Aided Civil and Infrastructure Engineering, Vol. 34, No. 3, pp. 213-229, Mar. 2019.
[https://doi.org/10.1111/mice.12409]

-
X. Yang, H. Li, Y. Yu, X. Luo, T. Huang, and X. Yang, "Automatic pixel-level crack detection and measurement using fully convolutional network", Computer-Aided Civil and Infrastructure Engineering, Vol. 33, No. 12, pp. 1090-1109, Aug. 2018.
[https://doi.org/10.1111/mice.12412]

- K. Simonyan and A. Zisserman, "Very deep convolutional networks for large-scale image recognition", CoRR, Sep. 2014.
-
K. Zuiderveld, "Contrast Limited Adaptive Histogram Equalization", Academic Press Professional, Inc., Graphics gems IV, San Diego, CA, USA, pp. 474–485, 1994.
[https://doi.org/10.1016/B978-0-12-336156-1.50061-6]

- V. Nair and G. E. Hinton, "Rectified linear units improve restricted boltzmann machines", Int. Conf. on Machine Learning, ICML 2010, Haifa, Israel, pp. 807-814, Jun. 2010.
- D. C. Lee and B. J Park, "Comparison of deep learning activation functions for performance improvement of a 2D shooting game learning agent", Journal of IIBC, Vol. 19, No. 2, pp. 135-141, Apr. 2019.
- S. Ioffe and C. Szegedy, "Batch normalization: Accelerating deep network training by reducing internal covariate shift", Int. Conf. on Machine Learning, ICML 2015, Lille, France, Vol. 37, pp. 448-456, Jul. 2015.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov, "Dropout: A simple way to prevent neural networks from overfitting", Journal of Machine Learning Research, Vol. 15, No. 1, pp. 1929-1958, Jan. 2014.

2012 : Degree in Dept. of Engineering & Information Technology.
2008 ~ 2017 : Worked in Research & Training Institute (Software Development)
2017 ~ 2019 : Student of MS degree in Dept. of Electrics Eng, Chonnam Natioanl University
Research interests : Digital Signal Processing, Machine Learning, Information Security, Cyber Security

2017 : Founder of FTEN company, Korea
2018 : MS degree, in Dept. of Electronics Eng, Chonnam National University
2018 : Student of Ph.D degree, in Dept. of Electronics Eng, Chonnam National University
Research interests : Digital Signal Processing, Image Processing, Speech Signal Processing, ML, DL

1977 : BS, Dept. of Electronics Engineering, Seoul National University.
1986 : M.S. & Ph.D. Dept. of Electrical & Computer Engineering, University of Iowa, USA
1987 ~ present : Professor, Dept. of Electronics & Computer Engineering, Chonnam National University, Korea
Research Interests : Intelligent Control, Sensor Signal Processing, Microprocessor Based Systems

1986 : BS degree, in Dept. of Electronics Eng, Seoul National University
1988 : MS degree, in Dept. of Electronics Eng, Seoul National University
1994 : Ph.D degree, in Dept. of Electronics Eng, Seoul National University
Research interests : Digital Signal Processing, Image Processing, Speech Signal Processing, Machine Learning

1995 : BS degree, in Dept. of Electronics Eng, Chosun University
1998 : MS degree, in Dept. of Electrical Eng, New Mexico State University, USA
2004 : Ph.D degree, in Dept. of Electrical Eng, New Mexico State University, USA
2010 ~ 2014 : Chief of Research Lab of Momed Solution
2015 ~ present : CEO of Wave3D
Research interests : Radar Signal Processing, Image Signal Processing, Drone Application