3D 비전 검사 시스템을 위한 간소화된 3D 카메라 캘리브레이션 알고리듬

Ⅰ. 서론

최근에 생산성 증가, 품질 향상, 인력 부족 등의 문제를 해결하기 위해서 비전 검사 자동화 시스템 구축에 대한 연구가 활발하게 진행되고 있다[1]. 자동차 부품 제조 현장에서 주로 시행되는 용접은 가스 금속 아크 용접(GMAW, Gas Metal Arc Welding)이다. 가스 금속 아크 용접은 용접부의 산화를 방지하기 위하여 아르곤(Ar)이나 헬륨(He), 이산화탄소(CO₂)와 같은 불활성 기체를 이용하여 용융 금속을 주위의 공기로부터 보호하는 용접 방식이다. 보호 가스로 CO₂ 가스를 100% 사용할 때 CO₂ 용접이라고 한다. 차량에서 CO₂ 용접 부위는 사고 발생 시 치명적인 결과를 초래할 수 있으며 용접 불량에 대한 리콜은 제조사에 매우 큰 경제적인 손실을 야기한다. 해외의 선진 자동차 제조업체는 3D 비전 기술을 이용한 용접 검사 솔루션을 생산 현장에 적용하고 있으며 국내 업체에서도 비전 검사 시스템 도입을 적극적으로 진행하고 있다[2]-[4].

3D 비전 검사 시스템에서 3D 카메라는 제품의 형상 정보를 획득하는 역할을 한다. 이 중 라인 레이저 기반의 3D 카메라는 광 삼각법(Optical Triangulation)을 이용한다. 라인 레이저가 검사 대상 위에 조사되면 카메라는 제품의 형상에 의해 변화된 라인 레이저의 형상을 영상으로 획득한다. 이 때 획득된 라인 레이저 형상의 데이터를 레이저 프로파일 데이터라고 한다. 카메라로 획득한 레이저 프로파일 데이터는 화소 단위이며, 3차원 공간에서의 높이 측정을 위해서 밀리미터 단위로 변환하는 과정이 필요하다. 이 때 화소 단위를 밀리미터 단위로 변환하기 위한 매개변수를 추정하는 과정이 3D 카메라 캘리브레이션(Calibration)이다. 3D 카메라 캘리브레이션은 크게 카메라 캘리브레이션과 3D 광 삼각법 캘리브레이션으로 구분된다. 카메라 캘리브레이션은 카메라의 내, 외부 매개변수와 렌즈에 의한 왜곡 계수를 추정한다. 일반적으로 많이 사용하는 방법은 Zhang의 방법이다[5]. 3D 광 삼각법 캘리브레이션은 라인 레이저가 만드는 레이저 평면 방정식을 추정하는 과정이다. McIvor는 레이저 평면 방정식과 카메라 내부 매개변수(Intrinsic Parameter), 외부 매개변수(Extrinsic Parameter)를 이용해서 영상 좌표에 대한 3차 방정식을 생성한 후 비선형 최소자승법(Nonlinear Least Square Method)으로 매개변수들을 추정한다[6]. 이 방법을 이용하기 위해서는 선형 이동이 가능한 실험 환경을 갖추어야 하며 서로 수직한 3개의 면을 가진 캘리브레이터를 준비해야 한다. Sanjeev는 카메라와 레이저 평면 간의 기하학적 관계를 이용해서 최소자승법으로 매개변수를 추정한다[7]. 이 방법들은 캘리브레이터의 형상이 복잡하며 제작 비용이 비싸다는 단점이 있다. Sun은 레이저 평면 방정식을 추정하기 위해 검은색의 정사각형이 그려진 평면 캘리브레이터를 사용한다[8]. 라인 레이저가 조사된 캘리브레이터의 영상을 다수 획득하고, 조사된 라인 레이저의 데이터를 모두 제어 점(Control Points)으로 사용하여 정확도를 향상하였다. Sun의 방법은 캘리브레이터의 제작이 용이하며 캘리브레이션 과정이 간단하다는 장점이 있다. 하지만 카메라 캘리브레이션과 3D 광 삼각법 캘리브레이션을 위해 별도의 캘리브레이터를 준비해서 다수의 영상을 획득해야하는 단점이 있다.

본 논문에서는 생산 현장에 적용하기 위한 간소화된 3D 캘리브레이션 알고리듬을 제안하며 이를 이용한 3D 비전 검사 시스템을 구현한다. 2장에서는 하나의 평면 캘리브레이터를 이용하여 카메라 캘리브레이션과 3D 광 삼각법 캘리브레이션을 동시에 수행하는 간소화된 3D 캘리브레이션 알고리듬을 기술한다. 3장에서는 3D 캘리브레이션 알고리듬의 정확도를 검증한다. 최종적으로 4장에서는 결론을 기술한다.

Ⅱ. 제안한 3D 카메라 캘리브레이션 알고리듬

2.1 카메라 캘리브레이션

카메라는 이상적인 핀홀 카메라 모델(Pin-hole Camera Model)과 달리 방사 왜곡(Radial Distortion), 접선 왜곡(Tangential Distortion)을 가진다. 카메라는 핀홀 카메라 모델에서 핀홀을 대신하여 렌즈를 사용한다.

렌즈의 굴절에 의해 발생하는 방사 왜곡은 그림 2와 같이 영상 평면의 중심에서 가장자리로 갈수록 영상 센서로 사영(Project)된 물체가 바깥쪽을 향해서 휘어지는 배럴 왜곡(Barrel Distortion)과 배럴 왜곡과 반대로 안쪽을 향해서 휘어지는 핀쿠션 왜곡(Pincushion Distortion)으로 분류된다.

Fig. 1.

Pin-hole camera model

Fig. 2.

Radial distortion

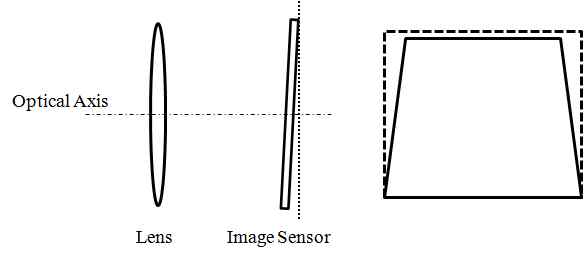
접선 왜곡은 그림 3과 같이 영상 센서가 광축(Optical Axis)과 물리적으로 완벽하게 정렬되지 못해 발생하는 왜곡이다. 접선 왜곡은 조립 공정 기술의 발전으로 방사 왜곡과 비교하면 상대적으로 매우 미약하다. 따라서 카메라 교정에서는 종종 방사 왜곡만을 교정하기도 한다.

Fig. 3.

Tangential distortion

비전 검사 시스템은 정확한 치수 측정을 위해서 카메라 캘리브레이션으로 왜곡을 교정해야 한다. 카메라 캘리브레이션을 위해 일반적으로 많이 사용하는 방법은 Zhang의 방법이다. 월드 좌표계의 한 점 [X_W, Y_W, Z_W]^T로부터 2D 영상 좌표 [x_p, y_p]^T로 변환하는 과정은 다음과 같다. 우선 월드 좌표계의 한 점 [X_W, Y_W, Z_W]^T로부터 카메라 좌표계의 한 점 [X_C, Y_C, Z_C]로의 변환은 식 (1)과 같다.

$\[ R\left[\begin{array}{c}\begin{array}{c}{X}_W\\ Y_W\end{array}\\ Z_W\end{array}\right]+T=\left[\begin{array}{c}\begin{array}{c}{X}_C\\ Y_C\end{array}\\ Z_C\end{array}\right] \]$

(1)

월드 좌표계와 카메라 좌표계 간의 관계는 회전 행렬 $$ R=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]$$과 이동 벡터 $$ T=\left[\begin{array}{c}\begin{array}{c}{t}_x\\ t_y\end{array}\\ t_z\end{array}\right]$$로 정의된다. 3차원인 카메라 좌표계에서 2차원의 영상 센서로의 사영 변환은 식 (2)와 같다.

$\[ \frac{1}{Z_C}\left[\begin{array}{c}{X}_C\\ Y_C\end{array}\right]=\left[\begin{array}{c}{x}_u\\ y_u\end{array}\right] \]$

(2)

이 때 [x_u, y_u]^T는 렌즈에 의한 왜곡이 존재하지 않는 무왜곡 좌표계(Undistorted Image Coordinates System)이다. 렌즈에 의한 방사 왜곡은 식 (3)과 같이 표준 다항식 모델을 이용하여 표현할 수 있으며 [x_u, y_u]^T는 왜곡 좌표계의 한 점 [x_d, y_d]^T로 변환된다.

$\[ \begin{array}{c}(1+k_1{r}^2+k_2{r}^4)\left[\begin{array}{c}{x}_u\\ y_u\end{array}\right]=\left[\begin{array}{c}{x}_d\\ y_d\end{array}\right]\hfill \\ \text{where} r=\sqrt{{x_u}^2+{y_u}^2},\hfill \end{array} \]$

(3)

왜곡 좌표계에서 영상 좌표계(Image Coordinates System)로의 변환은 식 (4)와 같다.

$\[ \left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{x}_d\\ y_d\end{array}\\ 1\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{x}_p\\ y_p\end{array}\\ 1\end{array}\right] \]$

(4)

이 때 $$ A=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]$$는 카메라 내부 매개변수이다. 카메라 내부 매개변수는 카메라의 가로, 세로 방향의 초점 거리를 의미하는 α, β, 영상 센서의 종횡비(Aspect Ratio)를 의미하는 γ, 광축과 영상 센서가 만나는 광점(Optical Point) (u₀, v₀)로 구성된다.

카메라 캘리브레이션으로 추정하는 매개변수는 카메라 내부 매개변수 행렬 A, 외부 매개변수인 회전 행렬 R과 이동 벡터 T, 왜곡 모델 계수 K = (k₁, k₂)이다.

카메라 캘리브레이션에 사용되는 캘리브레이터의 패턴은 그림 4와 같다. 실험에 사용된 패턴의 정사각형 한 변의 길이는 2mm이며 캘리브레이션을 위해 사용하는 특징 점(Feature Point)은 정사각형 사이의 교차점이다. 한 영상에서 사용하는 특징 점의 수는 총 360개(가로 24개, 세로 15개)이다. 캘리브레이션을 위해 캘리브레이터의 자세를 변경하면서 총 9장의 영상을 획득한다. 특징 점의 좌표와 좌표계 간의 변환 관계식을 이용하여 비선형 최소자승법으로 매개변수를 추정한다.

Fig. 4.

Planar calibrator pattern

2.2 3D 광 삼각법 캘리브레이션

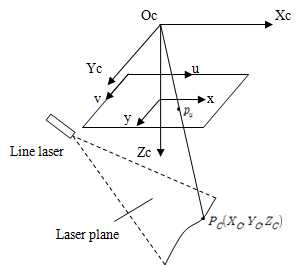
2차원인 레이저 프로파일 데이터의 영상 좌표를 3차원인 월드 좌표계로 변환할 때 카메라 캘리브레이션 과정에서 추정한 카메라 내부 변수와 왜곡 계수만으로는 부족하다. 그림 5에 나타낸 것과 같이 3차원 공간에 있는 무수히 많은 점들이 영상 센서 상에 한 점으로 투영되기 때문이다.

Fig. 5.

Image coordinate and laser plane

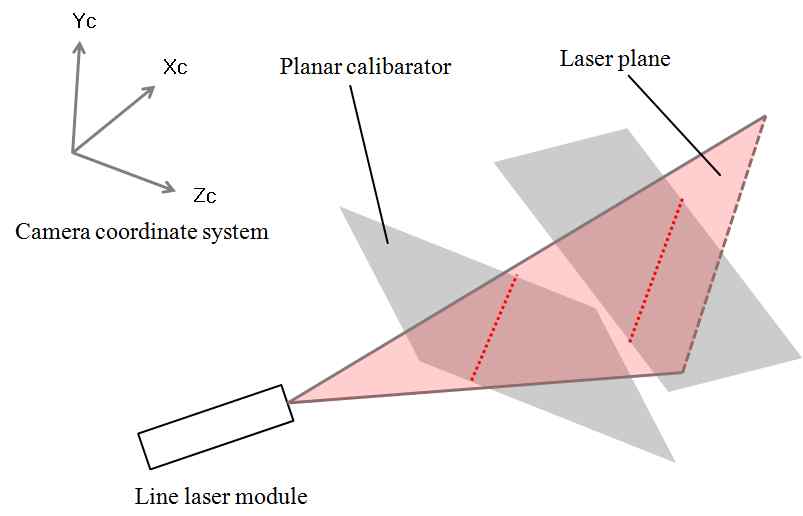
카메라 좌표계에서 라인 레이저가 만드는 레이저 평면의 방정식(ax+by+cz+d=0)을 알고 있다면 2차원의 좌표로부터 3차원 좌표로 변환이 가능하다. Sun은 광 삼각법 캘리브레이션을 위해 별도의 캘리브레이터를 제작하여 사용하였다. 본 연구에서는 그림 6과 같이 카메라 캘리브레이션 단계에서 평면 캘리브레이터의 영상 획득 시 라인 레이저를 조사하고 레이저 프로파일 데이터를 동시에 획득한다.

Fig. 6.

Line laser projected image

그림 7은 제안한 간소화된 3D 광 삼각법 캘리브레이션의 순서도이다. 평면 캘리브레이터의 2D 영상과 레이저 프로파일 데이터를 이용하여 카메라 좌표계 상의 라인 레이저가 만드는 평면의 방정식을 추정하는 과정은 다음과 같다.

Fig. 7.

3D optical triangulation calibration process

• 1) 카메라 캘리브레이션 단계에서 해당 2D 영상으로 추정한 평면 캘리브레이터의 회전, 이동변환 행렬을 불러온다.
• 2) 회전, 이동변환 행렬을 이용하여 평면 캘리브레이터 상의 특징 점 4개의 월드 좌표를 카메라 좌표계로 변환한다.
• 3) 카메라 좌표계로 변환한 4개의 특징 점을 이용하여 캘리브레이터의 평면 방정식을 계산한다.
• 4) 캘리브레이터의 평면 방정식을 이용하여 해당 영상에서의 프로파일 데이터를 모두 영상 좌표계에서 카메라 좌표계로 변환한다.
• 5) 카메라 좌표계로 변환한 프로파일 데이터를 제어 점으로 등록한다.
• 6) 각각의 2D 영상과 프로파일 데이터에 대하여 1~5의 과정을 반복 수행한다.
• 7) 모든 제어 점을 이용하여 그림 8과 같이 카메라 좌표계의 레이저 평면의 방정식을 추정한다.

Fig. 8.

Laser plane estimation

추정된 레이저 평면의 방정식을 이용하면 임의의 레이저 프로파일 데이터를 영상 좌표에서 카메라 좌표계로 변환 가능하다.

2.3 정확도 검증 방법

3D 캘리브레이션 알고리듬의 정확도 검증은 Sun의 방법을 이용한다[8].

• 1) 그림 9와 같이 배경 평면(background plane)에 놓인 게이지 블록(Gauge Block)에 라인 레이저를 조사하고 카메라를 이용하여 레이저 프로파일 데이터를 획득한다.
• 2) 평행한 두 직선 l, L의 영상 좌표를 카메라 좌표계로 변환하고 RANSAC(RANdom SAample Consensus) 알고리듬으로 카메라 좌표계에서 직선 식을 추정한다.
• 3) 추정된 두 직선 사이의 거리 s₁을 계산하고, 이미 알고 있는 게이지 블록의 높이 정보 d₁을 이용하여 배경 평면과 레이저 평면 사이의 각 alpha를 계산한다.

Fig. 9.

Verify accuracy

$\[ \alpha lpha=\text{arcsin}\frac{d_1}{s_1} \]$

(5)

본 연구에서는 alpha의 정확도 향상을 위하여 서로 다른 높이를 가진 게이지 블록 3개를 동시에 사용한다. 각각의 각을 계산한 후 평균값을 취한다. alpha값을 적용해서 측정된 게이지 블록의 높이와 이미 알고 있는 게이지 블록의 길이를 서로 비교해서 오차를 계산한다.

Ⅲ. 실험 및 고찰

연구에 사용된 카메라의 해상도는 가로, 세로 2048×1088이며, 한 화소의 크기는 가로, 세로 0.0055mm로 동일하다. 카메라 내부에는 레이저 프로파일을 검출하는 알고리듬을 포함하고 있어 사용자는 카메라의 출력을 2D 영상과 프로파일 데이터 중에서 선택할 수 있다.

카메라에 장착하는 렌즈는 Computar사의 M2518-MPW2이다. 이 렌즈는 초점거리가 25mm이다. 실험을 위해 조리개를 조정하여 동작거리(WD, Working Distance) 180mm와 220mm 사이에서 초점이 맺히도록 설정하였다.

라인 레이저는 MV micro사의 FP-Mvnano-660-70M–30-F200-TS이다. 레이저의 파장은 660nm이며 팬 각도는 30°이다.

3D 비전 검사 시스템을 위해 카메라와 라인 레이저를 고정할 브라켓을 설계, 제작하여 그림 11과 같이 3D 비전 검사 시스템을 구성한다.

Fig. 10.

Camera and line laser module

Fig. 11.

3D vision inspection system

브라켓에 카메라와 레이저를 장착하여 고정한 후 3D 카메라 캘리브레이션 알고리듬을 이용하여 매개변수를 추정하였다. 추정된 매개변수는 표 1과 같다.

Table 1.

3D camera calibration result

실험에 사용된 카메라의 초점 거리 (α, β)는 (5075.833, 5075.8828)이며, 광점 (u₀, v₀)는 (1050.055, 536.431)이다. 추정된 왜곡 계수는 k₁ = -0.199, k₂ = 1.985이다. 카메라 좌표계에서 레이저 평면식의 계수는 a = -0.000076, b = 0.012273, c = -0.005258이다. 레이저 평면과 배경 평면 사이의 각도 alpha = 1.288rad이다.

추정된 매개변수를 적용하여 기준면과 게이지 블록 사이의 높이를 측정한 값은 표 2와 같다.

표 2에서 보는 바와 같이 게이지블록 4개의 높이를 측정한 결과 최소 0.013mm에서 최대 0.056mm의 측정 오차를 가진다. 평균 측정 오차는 0.0315mm이다.

Table 2.

Height measurement result of gage block

아크용접이 적용되는 부위의 용접 각장(Leg Length)은 일반적으로 3mm 이상이며 산업 현장에서는 이보다 더 여유를 두고 관리한다. 그리고 산업 현장에서 용접 비드의 높이 또는 용접 덧붙임 두께를 측정하는데 주로 사용하는 용접 비드 측정게이지는 눈금이 1mm단위이다. 따라서 본 3D 비전 검사 시스템은 아크 용접부위의 각장을 측정하기에 적합함을 알 수 있다.

Ⅳ. 결론 및 향후 과제

본 논문에서는 간소화된 3D 카메라 캘리브레이션 알고리듬을 제안하고, 이를 이용하여 경제적인 비용으로 3D 비전 검사 시스템을 구현하였다. 간소화된 3D 캘리브레이션 알고리듬은 단일 평면 캘리브레이터로부터 획득한 영상과 레이저 프로파일 데이터를 이용해서 카메라 캘리브레이션과 3D 광 삼각법 캘리브레이션을 수행한다. 이는 광 삼각법 캘리브레이션을 위해 별도의 캘리브레이터를 제작할 필요가 없으므로 매우 경제적인 방법이다. 제안한 방법으로 3D 캘리브레이션을 수행하여 게이지 블록의 높이를 측정한 결과는 최대 0.056mm의 오차를 가진다. 이는 아크 용접부위의 각장 측정 및 용접 누락 유무를 판정하는 3D 비전 검사 시스템에 적용하기에 적합하다.

본 실험에서 사용한 3D 카메라는 레이저 프로파일 데이터를 검출하는 알고리듬이 FPGA로 구현되어 있다. 평면 위의 조사된 레이저의 중심선을 검출하는 과정에서 발생하는 레이저 프로파일 데이터의 표준편차가 측정 오차보다 높으므로 이를 감소시키기 위한 연구가 필요하다.

References

• Chang-Hyun Kim, Hong-Yeon Yu, Sung-Hoon Hong, and Jae-Yeol Kim, "A Study on Construction of Automatic Inspection System for Welding Flaws", Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 16(No. 6), p37-42, Dec.), (2007.
• Jong-Deuk Ahan, Sang-Zoon Byun, and Myung-Kil LEE, "Implementation of Inspection System for Vehicle Engine Harness using Vision Recognition", Proceedings of Korean Institute of Information Technology Summer Conference, p377-381, Jun.), (2014.
• Swoong-hwan Nam, and Yoon-ho Kim, "Development of Profile Analysis-based Vision System for Parts Inspection", Journal of Korea Institute of Information, Electronics, and Communication Technology, Vol. 5(No. 2), p74-80, Jun.), (2012.
• Cheol-Jin Jung, Kyung Moo Huh, and Jang Ki Kim, "3D Vision Inspection Algorithm using Geometrical Pattern Matching Method", Journal of Institute of Control, Robotics and Systems, Vol. 10(No. 1), p54-59, Jan.), (2004.
• Z. Zhang, "A flexible new technique for camera calibration", IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22(No. 11), p1330-1334, Nov.), (2000. [https://doi.org/10.1109/34.888718]
• Alan M. McIvor, "Nonlinear calibration of a laser stripe profiler", Optical Engineering, Vol. 41(No. 1), p205-212, Jan.), (2002. [https://doi.org/10.1117/1.1416694]
• S. Kumar, P. K. Tiwari, and S. B. Chaudhury, "An optical triangulation method for non-contact profile measurement", Proceedings of IEEE International Conference on Industrial Technology, p2878-2883, Dec.), (2006. [https://doi.org/10.1109/ICIT.2006.372653]
• Q. Sun, Y. Hou, Q. Tan, and G. Li, "A flexible calibration method using the planar target with a square pattern for line structured light vision system", PLoS One, Vol. 9(No. 9), Paper No. e106911 Sep.), (2014.