비유사성 측정을 위한 준거리 연산

Ⅰ. 서 론

군집화를 포함한 많은 데이터 분석에 비유사성 측정이 사용된다[1][2]. 흔히 비유사성(Dissimilarity), 유사성, 거리, 근접성(Proximity) 등을 구분하지 않고 사용하지만 각각은 다소 다른 의미를 갖는다. 거리는 떨어진 정도를 나타내므로 유사성을 직접 나타내지 않는다. 유사성 s는 거리 r의 역수를 이용해서 s = 1/(1 + r) 형태로 사용한다[1][3]. 근접성은 가깝다는 의미를 내포하므로 유사성을 나타내는 다른 말이나 비유사성/유사성을 포괄하는 의미로 종종 사용한다. 비유사성은 대상의 다른 정도를 나타내므로 거리에 의해 직접 측정할 수 있는 것이다.

데이터를 분석하는 행위는 결국 패턴 찾기다. 모든 것이 같다면 아무 할 일이 없다. 데이터 분석의 많은 응용은 각자가 가진 고유한 방법에도 불구하고 거리 즉 비유사성을 측정을 전제로 한다. 덩어리를 찾아내는 군집화, 어디에 속하는지를 찾는 분류는 물론이고 요즘 많이 연구되는 추천시스템 들은 우선 거리를 측정하는 것에서 시작한다. 그런데 거리를 측정하는 것이 항상 가능한 것은 아니다. 예를 들어 두 사람의 취향이 비슷한지를 알려면 거리를 재야하는데, 취향을 잰다는 것이 쉽지는 않다.

본 논문은 비유사성을 측정할 수 있는 거리 연산에 관한 것이다. 먼저 데이터 과학의 제 분야에서 일반적으로 사용하는 거리 연산에 대해 알아보고, 떨어진 정도를 나타내는 거리 척도를 위한 수학적 정의와 조건이 완화된 거리에 대해 소개한다. 다음으로 주어진 데이터에서 준거리 관계를 생성하는 행렬연산 min_sum을 제안하고 증명한다. 이를 데이터 군집화에 적용하여 비유사성 측정 수단으로서 효과를 정성적으로 평가한다. 제안한 준거리 연산을 사용하는 경우 국가 사이의 교역량, 사람들 사이에 주고받은 문자 횟수 등 일반적으로 거리를 정의하기 어려운 데이터에 거리 개념을 부여하여 분류 및 군집화 등을 수행할 수 있다.

Ⅱ. 준거리 생성을 위한 행렬연산 min_sum

이 장에서는 거리에 대한 일반적인 정의와 비유사성 측정을 위해 흔히 사용하는 거리함수에 대해 설명한다. 다음으로 새로운 행렬연산 min-sum을 제안하고 이것이 준거리 조건을 만족하는 거리행렬을 생성함을 증명한다.

2.1 거리에 대한 정의

분류, 군집화, 추천시스템 등 데이터 분석의 많은 분야는 대상의 비유사성을 측정하기 위해 다양한 거리 척도를 사용한다. 많은 응용에서 사용하는 거리 척도는 다음과 같으며 이들의 일반적인 특징에 대해 오랫동안 연구되어 왔다[4]-[6].

Table 1.

Distance functions

항상 그렇듯이 모든 데이터의 비유사성을 잘 측정하는 거리 척도는 없으며 응용에 따라 다르게 평가된다[2][5][7]. 하지만 이들은 거리를 측정하는 함수로서 모두 일정한 조건을 만족한다. 비유사성을 위한 거리 척도로서 거리함수는 일반적으로 다음과 같이 정의한다.

정의1 집합 X와 함수 d : X×X→[0,∞)가 모든 x, y, z∈X에 대하여 다음 네 가지 조건을 만족하면 d를 X위의 거리 혹은 거리함수 라고 한다.
(M1) d(x,x) = 0
(M2) d(x,z) ≤ d(x,y) + d(y,z)
(M3) d(x,y) = d(y,x)
(M4) d(x,y) = 0이면 x = y이다.

함수 d가 M1, M2 두 조건만 만족하면 준거리(Quasi-distance)라 부르고, d가 M1, M2, M3 세 조건을 만족하면 왜곡거리(Pseudo-distance)라 부른다. 준거리와 왜곡거리는 거리의 개념을 더 일반화한 것이다. 특히 준거리는 비유사성 측정을 위한 척도의 최소 조건을 만족한다[5][8]. 표 1에서 앞에서부터 5개는 모두 정의1을 만족하는 거리함수다. 반면에 상관계수 r_ij(*)와 cosα(**)는 유사성을 나타내는 것으로 거리가 아니다. 따라서 비유사성 척도로 사용할 때는 다음과 같이 변환한다.

$\[ D_{ij}=-\log \left(\left(r_{ij}/2\right)+0.5\right) \]$

(1)

거리함수를 이해하기 위해 몇 가지 사례를 설명한다. 어떤 집합 X에 대하여 X ×X위에서 $$ d\left(x,y\right)=\left\{\begin{array}{cc}1,& x\ne y\\ 0,& x=y\end{array}\right.$$로 정의된 함수는 정의1을 모두 만족하므로 X위의 거리다. 다음으로 정수의 집합 Z에 대하여 Z ×Z위에서 로 정의된 함수는 예를 들어 d(1,3) ≠ d(3,1)이므로 조건 M3를 만족하지 않아서 거리가 아니다. 하지만 다른 조건들은 모두 성립하므로 준거리이다. 마지막으로 평면 R²위의 두 점 x= (x₁, y₁ ), y =(x₂, y₂)에 대하여 d(x,y) = |x₁ - y₁|으로 정의된 함수는 M1, M2, M3를 만족하므로 왜곡거리이다. 하지만 서로 다른 두 점에 대하여 d((2,2),(2,3)) = 0이므로 M3를 만족하지 않아 거리가 아니다.

Ⅲ. 성능 평가 및 분석

비유사성/유사성에 대해서는 주로 통계학의 분야에서 70년대까지 잘 정리되었다. 이어진 연구들은 특정 문제와 관련해서, 데이터 유형 즉, 수치데이터, 이진데이터, 범주형데이터, 혼합형데이터 등을 대상으로 비유사성 척도들을 어떻게 활용하는지 등에 관한 것이다[8][9]. 비유사성 척도를 정량적으로 비교하기는 어렵다. 비유적으로 사람을 비교하는데 키와 몸무게 중 어떤 것이 유용한지는 어디에 사용하느냐에 달린 문제다. 여기서는 ⊕연산이 상대적인 거리를 효과적으로 측정한다는 것을 정성적인 방법으로 보인다. 앞의 사례를 잘 살펴보면 직관적으로 a₃는 a₄ , a₂보다 a₁과 가깝다고 생각되지만 이를 정량적으로 판단하려면 거리를 구할 수 있어야 한다. 하지만 앞에서 본 것과 같이 주어진 데이터 항목의 거리관계를 나타낼 마땅한 방법이 없다. 대신 제안한 ⊕연산을 사용하여 준거리를 생성할 수 있음을 알았다.

그림 1은 이렇게 구한 행렬 F⊕F의 거리 관계를 MDS(Multi-Dimentional Scaling)을 이용해서 나타낸 것이다. MDS는 비유사성 즉, 거리가 정해진 데이터를 시각적으로 나타내는 일종의 그래프 레이아웃이다[3]. 넓은 의미에서는 높은 차원 데이터의 차원을 낮추는 것인데, 여기서는 평면에 나타내는 것이므로 2차원으로 낮춘다. 즉, 거리행렬을 입력으로 받아서 데이터 들 사이의 거리를 가장 잘 반영하는 좌표를 생성해준다. R 프로그래밍에서 제공하는 cmdscale() 함수를 사용하여 거리관계를 시각적으로 나타냈다. 그림은 a₃와 a₁이 상대적으로 가깝다는 것을 보여준다.

Fig. 1.

Visualization distance relation in F⊕F

이상으로 ⊕연산으로 준거리를 생성하고 그것을 시각적으로 나타내 보았다. 이제 더 복잡한 데이터 집합의 군집화에 제안한 연산을 적용해 본다. 사용한 데이터는 미국 상원의 기명 투표 데이터다(http://www.voteview.com). 미국 상원 의원은 공화당, 민주당, 무소속으로 구성된다. 여기서는 투표 데이터를 군집화 하여 투표성향과 소속정당의 관계를 알아보려고 한다. 즉, 의원들의 법안에 대한 투표 데이터를 이용하여 의원들 사이의 거리를 구한 후 소속정당과 함께 시각적으로 나타내었을 때 군집이 형성되는지 알아보려 한다.

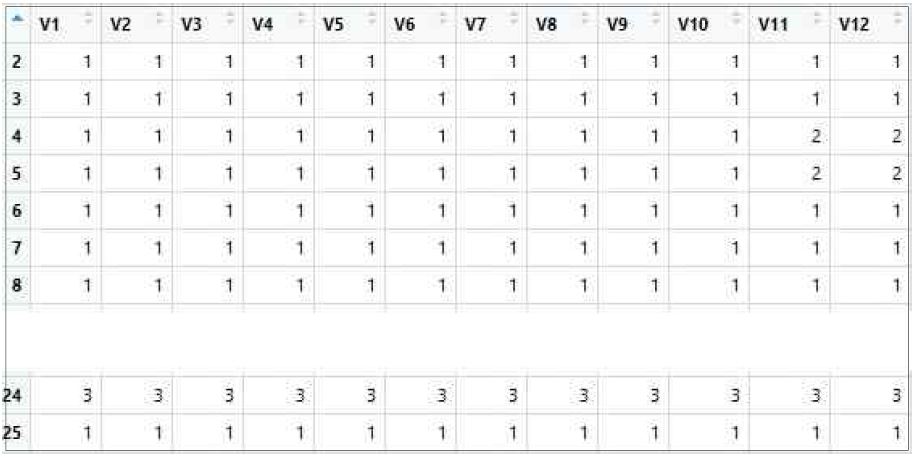
원 데이터의 편집과 클러스터링 과정은 참고문헌[3] 9장의 절차를 참고하였다. 표 2는 의원-투표 데이터 행렬을 나타낸다. 109번 회기를 기준으로 이 행렬의 크기는 101×644이다. 즉, 의원 101명이 644건의 법안에 투표한 결과다. 여기서 1은 찬성, 2는 반대, 3은 기권을 나타낸다. 어떤 두 의원의 벡터열이 일치할수록 두 의원의 투표성향이 같다고 할 수 있다. 따라서 일치하는 정도를 거리로 나타내면 투표성향이 같은 의원은 가까이 위치할 것이다. 이 때 각 의원의 위치를 소속정당으로 표시하면 투표 성향이 같은 사람들이 어떻게 분포하는지를 알 수 있다.

Table 2.

Senator-Vote data matrix

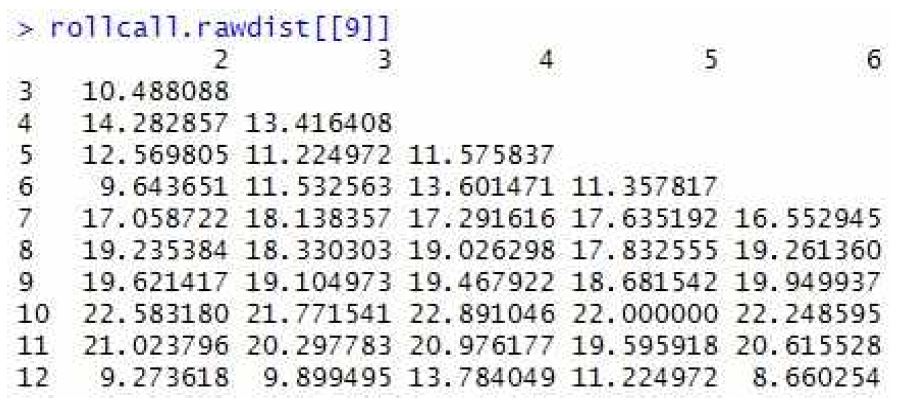
[3]에서는 의원들 사이의 거리를 의원-투표 행렬의 행 벡터별 유클리드 거리를 계산하여 측정하였다. 그림 2는 R 프로그램 결과를 나타낸다.

Fig. 2.

Distance of senators(Euclid)

예를 들어 2번 의원(첫 번째)과 3번 의원 사이의 거리가 약 10임을 나타낸다. 또한 거리행렬은 대칭이므로 하삼각행렬로 표시되었음을 알 수 있다.

이제 이렇게 계산한 의원들 사이의 거리를 2차원 평면에 펼쳐놓으면 그들의 소속정당별 분포를 알 수 있다. 그러기 위해서 MDS를 적용하여 각 의원들의 좌표를 구한 결과는 표 3과 같다. 예를 들어 SHELBY의원은 민주당 소속이고 상대적 거리를 고려했을 때 위치좌표는 대략 (7.5, 0.95)임을 나타낸다.

Table 3.

Coordinate of senators(Euclid)

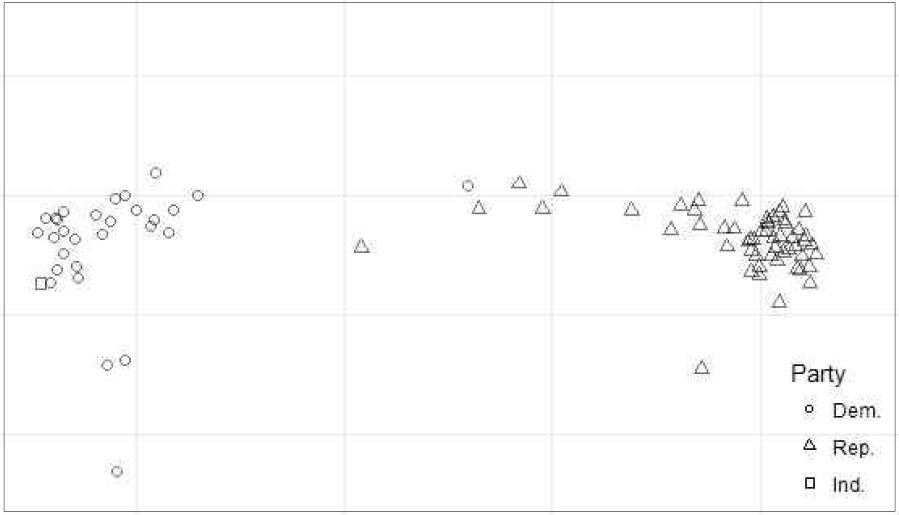
이 결과를 시각화 하면 그림 3과 같다. 왼쪽에 민주당, 오른쪽에 공화당 의원이 군집을 형성함을 알 수 있다.

Fig. 3.

Cluster(Euclid)

제안한 min-sum 연산을 적용하려면 먼저 의원들 사이의(잠재적) 거리를 나타내는 의원-의원 행렬을 구해야 한다. x-y 관계를 나타내는 데이터 행렬 M 이 주어지면 M*M^T와 M^T *M은 각각 x-x및 y-y관계를 나타내는 행렬이 된다(여기서 *는 행렬의 곱, M^T는 전치행렬). 따라서 의원-투표 행렬로부터 의원-의원 행렬을 구할 수 있다. 물론 이 행렬은 정의1의 거리조건을 만족하지 않으므로 거리 척도로 사용할 수 없다. 기존의 연구에서는 이렇게 얻은 의원-의원 행렬에 대해 행 벡터별 유클리드 거리를 계산하여 거리 행렬을 만드는 번거로운 과정을 거친다[3][7].

이제 의원들 사이의 준거리를 만들어 보자. 의원-투표 행렬을 M이라 하면, 의원-의원 행렬 N=M*M^T을 얻을 수 있다. 행렬 N의 대각성분을 0으로 수정한 행렬을 N(0)라 하면 정리2에의해 준거리 Q = [N(0)⊕N(0)]^m를 얻을 수 있다. 실제로 이 경우 m = 1이다. 그림 4, 표 4, 그림 5는 이렇게 구한 준거리 행렬 Q를 같은 방법으로 MDS로 시각화한 것이다.

Fig. 4.

Distance of senators(min_sum)

Table 4.

Coordinate of senators(min_sum)

Fig. 5.

Cluster(min_sum)

그림 3과 마찬가지로 의원들의 투표성향이 소속 정당별로 군집을 형성함을 알 수 있다. 즉, 제안한 연산으로 생성한 준거리가 데이터의 특정속성을 분석하기에 적절함을 알 수 있다.

Ⅳ. 결 론

분류, 군집화, 추천 같은 데이터 분석의 다양한 분야가 데이터 항목의 비유사성 즉, 거리 측정을 필요로 한다. 데이터 집합의 거리관계는 항목들의 거리를 나타내는 거리행렬로 나타낼 수 있다. 데이터 집합이 항목-값 행렬로 주어지는 경우, 보통 항목벡터들의 유클리드 거리, 상관계수, 코사인 유사도 등을 이용하여 거리행렬을 구하는데, 이는 계산량이 많기도 하고, 직관적이지도 않다. 이 논문에서는 데이터 집합으로부터 직관적으로 만든 잠재적 거리행렬을 준거리 조건을 만족하는 행렬로 변환하는 행렬연산 min_sum을 제안하고, 이 연산을 반복 적용하면 준거리 행렬로 수렴함을 증명하였다. 제안한 연산을 군집화에 적용한 결과 종전의 방법과 같이 거리 척도로서 효과적임을 확인하였다.

이 논문에서는 제안한 행렬연산 min_sum이 거리 조건을 만족하지 않는 행렬을 준거리 조건을 만족하는 행렬로 변환함을 증명하고, 그렇게 얻어진 거리행렬이 비유사성을 효과적으로 측정함을 실제 문제에 적용하여 정성적으로 확인하였다. 다음으로 동일한 데이터에 대해 통상의 방법으로 생성한 거리행렬과 제안한 연산을 적용하여 생성한 준거리 행렬을 데이터 유형별로 분석하는 연구와 계산 복잡도를 비교하는 연구가 수행될 수 있겠다.

Acknowledgments

이 논문은 2016년도 광운대학교 교내학술연구비 지원에 의해 연구되었음

References

• A. D. Gordon, "Classification : Methods for the Exploratory Analysis of Multivariate Data", Measuring Dissimilarity, Chapman and Hall, Chap 2, p13-32, (1981).
• Rui Xu, and Donald Wunsch II, "Survey of Clustering Algorithms", IEEE Transactions on Neural Networks, 16(3), p645-678, May), (2005.
• Drew Conway and John White, "Machine Learning for Hackers", O'Reilly Media, p241, Feb), (2012.
• J. C. Gower, "A General Coefficient of Similarity and Some of Its Properties", Biometrics, 27(4), p857-871, Dec), (1971. [https://doi.org/10.2307/2528823]
• J. C. Gower, and P. Legendre, "Metric and Euclidean Properties of Dissimilarity Coefficients", Journal of Classification, 3(1), p5-48, Mar), (1986. [https://doi.org/10.1007/bf01896809]
• Guojun Gan, Chaoqun Ma, and Jianhong Wu, "Data Clustering : Theory, Algorithms, and Applications, Similarity and Dissimilarity Measures, ASA-SIAM Series on Statistics and Applied Probability", SIAM, Philadelphia, ASA, Alexandria, VA, p67-106, (2007).
• Segaran, and Toby, "Programming Collective Intelligence: Building Smart Web 2.0, Applications", O’Reilly Media, p14, (2007).
• Brian S. Everitt, Sabine Landau, Morven Leese, and Daniel Stahl, "Cluster Analysis", 5th Ed., John Wiley & Sons, Ltd, p49, (2011).
• Charu C. Aggarwal, and Chandan K. Reddy, "Data Clustering Algorithms and Applications", CRC Press, p7, (2014).