완전 동형 암호 라이브러리의 성능 분석

Ⅰ. 서 론

4차 산업 혁명으로 학문과 기술의 경계가 없어지는 추세이며 다양한 분야의 기술이 융합되어 새로운 기술의 혁신이 이루어지고 있는 상황이다. 특히, 빅데이터, 인공지능, 사물 인터넷 등의 기술은 데이터의 활용 및 분석을 통해 다양한 분야에 적용되고 있다. 대량의 데이터수집 및 분석과정은 네트워크상에서 이뤄지고 있으며 데이터들 중 일부는 인간의 개인정보 또는 국가와 기업의 핵심정보와 관련이 있을 수 있다. 이러한 경우에는 해당 데이터들에 대한 철저한 보안 관리가 없을 경우, 정보 유출 사고로 인한 피해가 발생할 확률이 매우 높다.

개인정보 및 국가, 기업의 핵심 정보 보호를 위해 현재는 해당 정보들을 암호화하여 저장하는 방식을 취한다. 또한 이러한 데이터들의 접근은 인가 받은 곳에서만 허용하도록 통제하고 있다[1]. 하지만 현존하는 암호 알고리즘을 사용할 경우, 암호화된 정보들을 이용하여 검색이나 통계처리 연산을 수행하기 위해서는 그들을 모두 복호화 후 연산을 수행해야 한다. 따라서 연산과정에서 평문이 유출될 가능성이 존재한다. 이를 해결하기 위해 데이터의 안전한 저장을 보장하면서 복호화 없이 데이터 처리를 가능하게 하는 완전 동형 암호화의 필요성이높아지고 있다.

현재 완전 동형 암호(FHE, Fully Homomorphic Encryption)는 IBM과 Microsoft를 포함한 선도 연구집단에서 라이브러리로 제공하고 있다. 해당 라이브러리를 이용한 다양한 연구가 진행 중이나[2], 불행히도 각 라이브러리들의 성능 비교에 관한 연구가 많이 이루어지지 않고 있다. 본 연구에서는 라이브러리를 사용하고자 하는 목적에 따라 필요한 기초자료를 제공하기 위해 대표적인 완전 동형 암호 라이브러리인 HElib[3], TFHE[4] 그리고 SEAL[5]을 이용해 암호화된 상태에서 산술 연산의 기본 연산인 덧셈 연산과 암호화된 데이터들에 대한 연산 순서 및 흐름 제어에 사용할 수 있는 비교 연산을 구현하고 성능평가를 진행한다. 이때 덧셈 연산은 다수개의 암호문을 덧셈 연산하며 비교 연산은 2와 1024bit 범위의 암호문을 비교 연산한다.

덧셈 연산에서 HElib과 TFHE는 숫자를 비트 단위로 표현하므로 현재, 완전 동형 암호를 이용하여 다수 개의 암호문을 가장 효율적으로 더하는 방식이라고 알려진 Full Adder와 KSA(Kogge Stone Adder) 방식을 혼용한 [6]의 방법을 이용해 구현한다. 하지만 SEAL은 비트 단위로 표현한 평문 값을 암호화하여 AND 연산을 반복적으로 수행할 시 암호문의 잡음(Noise)으로 인해 정확한 연산 결과를 얻을 수 없다는 문제가 있다. 또한, 암호문의 잡음을 제거하는 기능인 bootstrapping이 지원되지 않아 암호문의 잡음을 제거할 수 없다. 따라서 SEAL에서는 KSA를 적용한 방식 대신 정수로 숫자를 표현한 암호문의 덧셈 연산을 지원하는 함수 ‘add()’로 연산을 수행한다.

비교 연산은 KSA를 응용한 연산 방법을 본 연구에서 제안하였다. KSA 연산 결과에서 자리 올림이 발생하면 carry가 1이 되고, 자리 올림이 발생하지 않을 시, carry는 0이 되는 원리를 적용하였다. 값을 담고 있는 암호문은 비교 연산의 마지막에 결과 값으로 얻을 수 있으며 3장의 그림 8의 알고리즘으로 구현하여 성능을 비교하였다. 제안된 방식은 HElib과 TFHE에 적용할 수 있으며, SEAL에서는 암호문의 잡음을 제거할 수 없는 기술적 한계로 적용이 불가한 것으로 파악되었다. 자세한 구현 방법은 3장 성능 비교에서 소개한다.

본 논문에서 평가한 라이브러리의 실험 환경은 Intel i7-6700 3.40GHz, 16.0GB RAM이며, HElib과 TFHE는 Ubuntu 14.04 LTS, SEAL은 Windows 10pro이다.

HElib, TFHE 그리고 SEAL에서 덧셈 연산 비교 결과, 비트 단위에서 6개 이상의 수를 가산할 때는 HElib이 TFHE보다 빠르며 SEAL은 HElib보다 1600배 이상 빠른 속도로 덧셈 연산을 수행하는 것을 확인할 수 있었다. 비교 연산에서는 256bit 이하의 값 비교에서는 TFHE가 HElib보다 더 빠른 속도로 연산이 수행되는 것을 확인할 수 있었다.

본 논문의 2장에서는 라이브러리의 설명과 특징을 소개하고 3장에서는 라이브러리별로 덧셈 연산과 비교 연산의 성능을 비교한다. 4장에서는 라이브러리의 연산 결과를 비교하고 5장에서는 결론을 내린다.

Ⅱ. 라이브러리 소개

완전 동형 암호는 복호화 과정을 거치지 않고서도 임의의 형태로 연산의 결과 값에 대응되는 암호문을 생성할 수 있는 암호화 방식을 말한다.

본 장에서는 기존의 가장 대표적인 완전 동형 암호 라이브러리로 알려진 GHS[7] 방법을 적용한 IBM에서 적용한 HElib, GSW의 Ring-variant[8]를 적용한 오픈 소스 라이브러리인 TFHE, 최근 Microsoft에서 제안하였으며 FV 방법(Fan-Vercauteren Scheme)[9]을 적용한 SEAL의 암호화 파라미터를 포함한 특징과 차이점을 소개한다.

HElib[3]은 IBM에서 제안하였으며 BGV[10] 방법을 개선한 GHS[7] 방법을 적용한 C++ 기반의 완전동형 암호 라이브러리이다. 멀티 쓰레딩(Multi-Threading)을 지원하며, 덧셈, 곱셈, 비트 단위 이동 연산자와 같은 저 수준의 기능을 제공한다. 구현을 위해서는 슬롯의 개수, 보안 수준, L(최대 연속 수행한 AND 연산의 횟수), B(AND 연산 한 회 수행했을 때 발생하는 노이즈의 양) 파라미터의 설정이 필요하다.

HElib은 여러 개의 메시지를 하나의 암호문으로 암호화하는 암호문 패킹(Packing) 기술을 사용하여 효율적 계산을 수행하는 SIMD 방식으로 사용, 연산시간과 암호문의 수를 줄일 수 있는 병렬 계산의 이점을 제공한다.

TFHE[4]는 GSW의 Ring-variant[8]를 구현한 완전동형 암호 오픈 소스 라이브러리[11]이며, 일반 PC환경에서 완전 동형 암호 알고리즘의 성능에 가장 큰 영향을 미치는 bootstrapping 연산을 0.1초 이내 수행되도록 성능을 대폭 개선하였다. 또한 bootstrapping key의 크기를 1GB에서 24MB로 줄여 security level을 유지하는 동시에 잡음이 발생할 때생기는 오버헤드를 감소시켰다.

사용하는 파라미터는 비밀키를 생성하는 데 필요한 lambda가 있으며, 파라미터의 설정에 따라 최소 110bit에서 최대 188bit의 security level을 제공한다. 현재 멀티 쓰레딩은 지원하지 않고 있으며, HElib과 마찬가지로 암호화된 비트 단위 평문이 존재하는 상태에서 연산이 가능한 NAND, OR, AND, XOR, XNOR, NOT, NOR 게이트 연산 방법을 제공하여 다양한 알고리즘 구현으로의 활용이 가능하다. HElib과 달리 TFHE는 기술적 문제로 패킹 기능을 제공하지 못하고 있다.

SEAL[5]은 2015년 Microsoft에서 제안하였으며 FV 방법[9]을 적용한 C++ 기반의 동형 암호 라이브러리로 Visual Studio 환경에서 사용이 가능하다. FV방법은 SecretKeyGen, PublicKeyGen, EvaluateKeyGen, Encrypt, Decrypt, Add, Mul과 Relin 알고리즘으로 구성되어있으며, SEAL에서 이 알고리즘들을 구현하였다. 기존의 HElib, TFHE가 비트 단위의 연산을 지원한 것과 달리, SEAL은 기본적으로 정수에서 동형 암호화 덧셈과 곱셈 연산 수행을 지원하기 때문에 산술 연산 알고리즘을 쉽게 구현할 수 있다. 사용하는 파라미터로는 poly_modulus, plain_modulus, coeff_modulus가 있으며, poly_modulus는 다항식의 모듈러스로 다항식 Xm+1형태로 R(Ring)을 결정하기 위한 파라미터이다. 여기서 m은 2의 거듭제곱형태이다. coeff_modulus는 다항식 계수의 모듈러스이며 plain_modulus는 평문을 표현할 때 사용되는 다항식의 계수의 모듈러스다. SEAL은 암호문 간 연산을 수행할 때마다 암호문의 잡음이 증가하는데 하나의 암호문이 내용이 변형되지 않고 감당할 수 있는 잡음의 정도인 Noise budget이 0보다 커야 하며 0에 도달하게 되면 복호화를 수행할 수 없다.

암호화를 처음 수행하여 생성된 암호문의 전체 Noise Budget은 매우 대략적으로 결정되고 coeff_modulus를 증가시키면 사용자가 암호문을 손상시키지 않으면서 암호문의 연산을 수행할 수 있다. 그러나 coeff_modulus를 증가시키면 보안 수준에 부정적인 영향을 미치기 때문에 신중히 고려해야 한다. 또한 SEAL에서는 암호문을 생성할 때 아주 적은 양의 불변 잡음(Invariant Noise)이 발생하게 되는데 v가 암호문의 불변 잡음 크기라 할 때 암호문의 Noise Budget은 log22v로 정의된다. 여기서 Noise Budget은 복호화를 바르게 수행할 수 있는 잡음의 최대치로 잡음이 특정 임계치를 초과하면 복호화가 올바로 수행되지 않는다. SEAL에서 처음 생성된 암호문의 Noise Budget은 log102(coeff_modulus/plain_modulus)-log22v이며 boot strapping 기능을 제공하지 않기 때문에 암호문의 Noise Budget을 회복할 수는 없다. 현재 버전 2.2까지 출시되었다.

Ⅲ. 성능 비교

본 장에서는 완전 동형 암호 방식을 지원하는 라이브러리인 HElib, TFHE 그리고 SEAL에서 암호화된 상태에서 산술 연산의 기본 연산인 덧셈 연산과 암호문의 실행 흐름을 제어할 수 있는 비교 연산의 성능을 실제 구현을 통해 비교한다.

덧셈 연산은 모든 연산에서 공통적으로 사용되는 산술 연산이며 곱셈 연산과 뺄셈 연산과 같은 사칙연산의 기본이 된다.

비교 연산은 데이터의 값의 비교를 통해 값을 처리하는 검색 및 분석 등의 작업에 필수적인 연산이다. 암호화된 상태에서의 비교 연산은 암호화된 정수를 입력으로 하고 암호화된 비교 결과 값을 출력한다. 그렇기 때문에 암호문의 비교 연산은 기밀성을 보장하면서 값의 비교를 통해 데이터의 실행 흐름을 제어할 수 있다.

HElib과 TFHE는 비트 단위 연산을 지원하므로 덧셈 연산의 구현을 위해 다수 개의 수를 가장 효율적으로 더하는 방식인 Full Adder와 KSA 방식[6]을 이용하여 덧셈 연산을 수행하며 비교 연산은 KSA 연산 결과의 자리 올림 값을 이용하여 구현한다.

그러나 SEAL은 2장 라이브러리 소개에서 설명한 Noise Budget을 고려할 때, 덧셈 연산과 비교 연산에서 공통적으로 사용하는 KSA를 이용한 구현을 할 수 없는 것으로 파악되었다. KSA는 nb bit의 수를 연산할 때 필요한 곱셈 횟수는 1+2log2nb번으로 2bit 연산 시 최소 3번의 곱셈 연산이 필요하다. 비트 연산이 가능하며 bootstrapping을 지원하는 TFHE와 HElib은 KSA와 Full Adder를 이용한 연산이 가능하지만 SEAL에서는 3회 이상 곱셈 연산 수행 시 암호문의 Noise Budget이 0에 도달하며 이때 bootstrapping을 지원하지 않아 암호문의 잡음을 제거할 수 없어 KSA 방식이 대신 SEAL에서 제공하는 기능을 통해 구현하였다.

연산을 수행하기 위한 각 라이브러리의 파라미터 설정으로는 HElib에서 slot = 1200, security level = 93, L = 25, B = 25로 설정했다. 1200 slot은 다른 slot의 설정보다 slot의 개수는 많지만, 격자 차원(Lattice Dimension)은 낮아 연산 속도가 빠르기 때문에 계산이 효율적이다. HElib에서의 평문의 공간은 GF(2²⁰)이다. TFHE에서는 비밀키를 생성하는데 필요한 파라미터 lambda를 100으로 설정하였다. SEAL에서는 poly_modulus = 1x^2048+1 (= x²⁰⁴⁸+1), plain_modulus=1<<8(= 2⁸), coeff_modulus= 2048의 파라미터를 사용한다.

표 1은 본 논문의 성능 비교와 구현을 위해 사용된 표기법과 설명을 정의 내린다.

Table 1.

Notation

3.1 덧셈 연산 성능 비교

본 절에서는 각 라이브러리를 이용하여 기본 산술 연산 타입인 정수 데이터 타입의 범위인 32bit와 정수 데이터 타입의 범위에서 64bit의 범위로 확장하여 수행한 다수 개의 덧셈 연산의 구현 방법, 소스 코드, 수행 결과를 살펴본다.

구현 방법: HElib과 TFHE는 Full Adder와 KSA방식을 이용해 구현한다. 구현 시 HElib은 패킹을 지원하므로 암호문 하나에 암호화된 이진수 전체를 저장하여 4.3MB 크기의 하나의 암호문으로 표현이 되지만 TFHE는 패킹을 지원하지 않기 때문에 1비트의 평문을 암호화하여 배열의 한 칸에 저장한다.

다수 개의 덧셈 연산 알고리즘을 설명한 그림 1의 내용은 다음과 같다. n이 3 이상일 때 Full Adder로 3개의 수를 더해 2개의 수로 줄이고 n이 2일 때 KSA로 최종 연산 값을 구한다.

Fig. 1.

Addition algorithm for multiple binary numbers

SEAL에서는 KSA와 Full Adder 대신 이진수 표현이 아닌 정수 타입을 암호화한 암호문의 덧셈을 함수 ‘add()’로 연산한다. 다수 개의 수를 더하기 위해서 'add()'를 add(add(n₁, add(n₂,n₃)),n₄)…형태로 반복적으로 호출하여 구현한다.

구현 상세: 위 설계에 따라 구현한 소스코드는 아래와 같다.

HElib은 32bit의 암호화된 이진수 n개를 배열 ic[]에 각각 저장하고 Full Adder로 ic[]에 저장된 3개의 수를 더해 2개의 결과로 줄이는 작업을 더하는 수가 3개미만으로 남을 때까지 반복한다. Full Adder와 KSA 수행 시 파라미터 값으로 들어가는 pubkey는 암호화에 사용되는 공개키, c는 이동 연산(Shift)에 필요한 context를 의미한다. Full Adder에서 ic[i*3], ic[i*3+1], ic[i*3+2] 수를 더한 결과는 ic[i*2], ic[i*2+1]에 저장한다. KSA에서는 ic[0], ic[1]의 값을 더해 result에 최종 저장한다. 표 2는 함수의 입력값과 출력 값을 나타낸다.

Table 2.

Parameters of functions used in HElib

HElib은 초기 설정한 파라미터 값에 의해 32bit연산까지 지원하므로 64bit 평문을 더하기 위해서는(32*2) 크기의 이차원 암호문 배열 ic에 32bit씩 나누어 암호화하여 저장한 뒤 덧셈 연산을 수행한다. HElib의 32bit 덧셈 연산과 같이 Full Adder로 배열ic에 저장된 3개의 수를 더해 2개의 결과로 줄이는 작업을 더하는 수가 3개미만으로 남을 때까지 반복한다. 높은 자리의 32bit 덧셈은 낮은 자리의 32bit 덧셈 연산의 자리 올림 값인 carry 값을 같이 가산하여 덧셈 결과를 도출한다.

Fig. 2.

Pseudocode for 32bit addition in HElib

Fig. 3.

Pseudocode for 64bit addition in HElib

TFHE는 임의의 nb 비트 길이의 암호화된 이진수 n개를 (n*nb) 크기의 이차원 배열 ic에 저장한다. Full Adder로 배열 ic에 저장된 3개의 암호문인 ic[n-1] [i], ic[n-2][i], ic[n-3][i]를 더해 ic[n-2][i], ic[n-3][i]에 저장하는 작업을 이진수의 개수가 3개미만이 될 때까지 반복한다. Full Adder와 KSA 수행시 파라미터 값으로 들어가는 keyset은 암호화에 필요한 키이다. Full Adder의 마지막 결과 값인 ic[0][i]와 ic[1][i]를 KSA에서 더해 result에 최종 저장한다. 표 3은 함수의 입력 값과 출력 값을 나타낸다.

Fig. 4.

Pseudocode for addition in TFHE

Table 3.

Parameters of functions used in TFHE

SEAL에서 임의의 nb 비트 길이의 0과 2^nb-1범위 내 암호화된 정수가 n개 있을 때, 크기가 n인 배열ic[]에 암호문 n개를 저장한 후, 함수 add()로 ic[i]와 ic[i-1]를 더해 ic[i-1]에 연산 결과를 저장한다. 이 과정을 연산 결과 값이 ic[0]에 저장될 때까지 반복한다. evaluator는 평문과 암호문을 변환시키기 위한 기능들을 포함한 클래스이다. 표 4는 함수의 입력값과 출력 값을 나타낸다.

Fig. 5.

Pseudocode for addition in SEAL

Table 4.

Parameters of functions used in SEAL

성능 비교: 표 5는 3개의 수를 더하기 위해 HElib과 TFHE에서 구현한 KSA와 Full Adder를 각1회씩 수행했을 때의 시간 측정 결과이다. KSA의 연산 시간은 HElib이 TFHE 보다 약 2배의 연산 시간이 소요되었으며 Full Adder의 연산 시간 측정에서는 TFHE가 HElib 보다 약 3배의 연산시간이 소요되는 것으로 파악되었다.

Table 5.

Execution time to add three numbers in HElib and TFHE

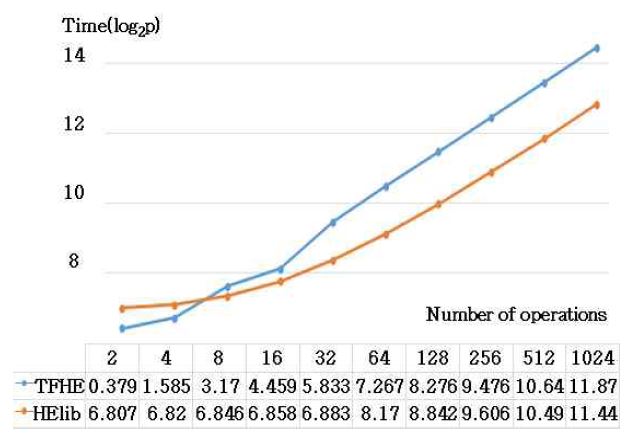
그림 6과 그림 7은 HElib과 TFHE에서 32bit 암호문 다수 개의 덧셈 연산과 SEAL에서 0과 232-1범위 내 십진수 암호문 다수 개를 덧셈 연산한 수행 결과이다. 가로축은 3에서 1024개의 범위의 연산한 수의 개수를 나타내고, 세로축은 수행 시간(초)을 나타내며 p를 실제 측정된 시간이라고 할 때 log2p로 나타낸다. HElib과 TFHE에서 덧셈 연산의 수행 시간은 KSA보다 Full Adder 수행 횟수에 영향을 많이 받기 때문에 가산 숫자의 개수가 커질수록 두 라이브러리의 실행 시간의 차이가 커진다.

Fig. 6.

Comparison of execution time for 32bit addition in HElib, TFHE

Fig. 7.

Comparison of execution time for 32bit addition in SEAL

따라서 이진수 n개의 덧셈 연산을 수행할 때 HElib은 약 (n-2)*t₂+t₁초가 소요될 것으로 예측되고 TFHE는 약 (n-2)*(3*t₂)+t1/2초가 소요될 것으로 예측되었다. 이를 바탕으로 한 실험 결과, 6개 이상의 수를 연산할 시에는 HElib이 TFHE보다 약 (-2n+4)*t₂+t₁/2초 빠른 덧셈 연산이 가능한 것으로 파악되었다.

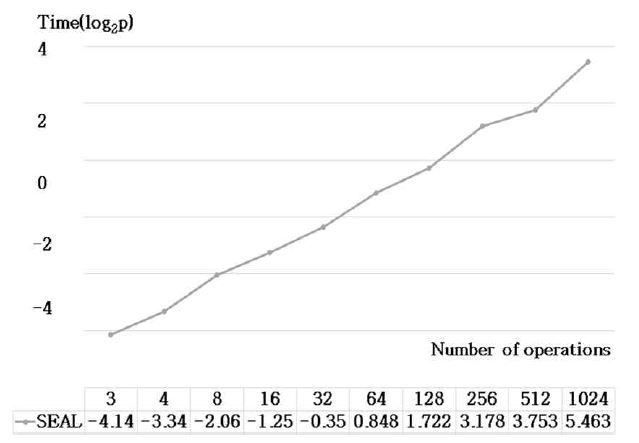
그림 7에서 보는 바와 같이 SEAL은 더하는 숫자의 개수가 증가함에 따라 실행 시간도 선형적으로 증가함을 보인다. SEAL은 HElib보다 약 1600배가 빠른 것으로 파악되었다.

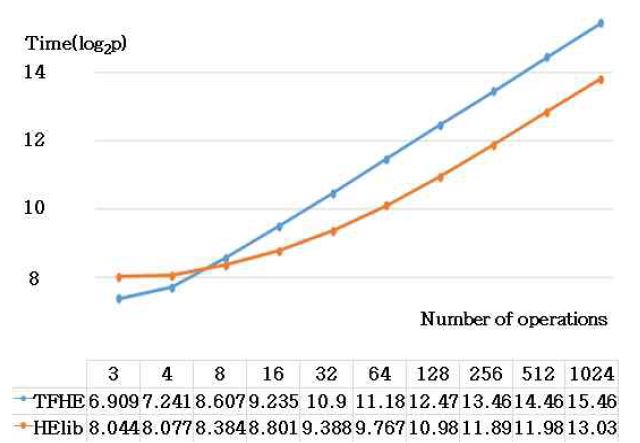
그림 8과 그림 9는 HElib과 TFHE에서 64bit 암호문 다수 개와 SEAL에서 0과 2⁶⁴-1범위 내 암호화된 십진수 다수 개를 덧셈 연산한 수행 결과이다.

HElib과 TFHE는 32bit 덧셈 연산 결과와 같이 연산의 수행 시간은 Full Adder 수행 횟수에 영향을 많이 받기 때문에 가산 숫자의 개수가 커질수록 두 라이브러리의 실행 시간의 차이가 커진다. 더하는 암호문의 수가 6개 이상일 땐 HElib이 TFHE보다 빠르게 덧셈 연산을 수행한다.

SEAL은 32bit 덧셈 연산과 마찬가지로 더하는 숫자의 개수가 증가함에 따라 실행 시간도 선형적으로 증가한다.

Fig. 8.

Comparison of execution time for 64bit addition in HElib, TFHE

Fig. 9.

Comparison of execution time for 64bit addition in SEAL

3.2 비교 연산 성능 비교

본 절에서는 각 라이브러리에서의 1024bit 범위의 암호화된 두 수의 비교 연산을 위한 구현 설계와 성능 비교 결과를 살펴본다.

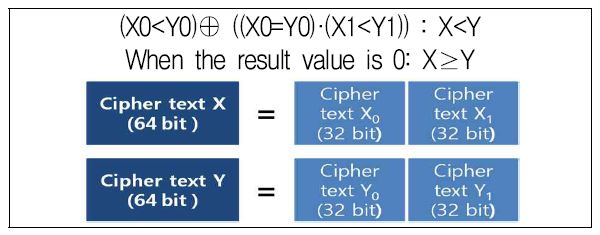
구현 방법: 본 논문에서 제안한 TFHE와 HElib의 이진수 비교 연산 방법은 다음과 같다. KSA 연산결과에서 자리 올림이 발생하면 carry가 1이 되고, 자리 올림이 발생하지 않을 시, carry는 0이 된다.

이를 적용한 그림 10의 비교 연산 알고리즘으로 n bit의 암호화된 이진수 X, Y 의 크기 비교 연산을 수행할 수 있으며 carry 값을 담고 있는 암호문을 비교 연산 마지막에 결과값으로 얻을 수 있다. 그림 10의 알고리즘으로 4bit의 암호화된 이진수 X, Y를 비교 연산하는 예는 그림 11과 같다.

Fig. 10.

Comparison algorithm for nb bit ciphertexts (X, Y: binary number encrypted with nb bits)

Fig. 11.

Example of 4bit comparison operation

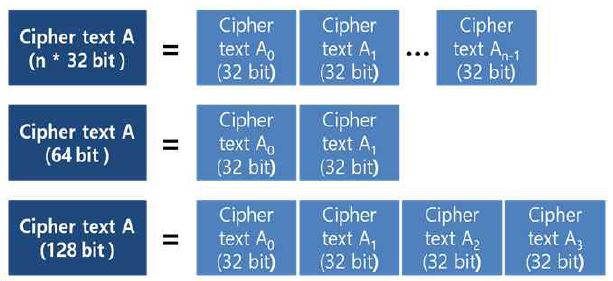
그러나 HElib은 초기 설정한 파라미터 값에 의해 32bit 연산까지 지원하므로 32bit 이상 (nb≥32)의 암호화된 이진수의 크기를 비교하기 위해서는 다수개의 32bit 암호문을 연결하여 사용한다. HElib에서 32bit 이상의 수를 비교 연산하는 방법은 다음과 같다. HElib에서 32bit 이상의 암호문은 그림 12와 같이 구성된다. 가장 높은 자릿수의 32bit 암호문을 A₀라하고 순차적으로 A₁, A₂,…, A_n-1로 지칭한다.

Fig. 12.

Form of ciphertext exceeded 32bit in HElib

32bit의 배수의 크기를 가지는 이진수들의 크기를 비교하기 위해서는 가장 높은 자릿수의 32bit 크기의 암호문 A0을 먼저 비교하고 암호문의 크기가 같을 땐, 그다음 32bit 암호문의 크기를 순차적으로 비교한다.

HElib에서 64bit의 암호화된 이진수 X, Y를 비교하는 예는 그림 13과 같다.

Fig. 13.

Example of 64bit ciphertext comparison operation in HElib

그림 14는 32bit의 배수의 길이를 갖는 평문이 32bit씩 NumOf32개로 나누어 암호화된 상태로 저장된 암호문 X, Y의 크기를 비교하는 알고리즘이다. 여기서 equalXY는 32bit의 단일 암호문 두 개의 숨겨진 평문의 값이 같은지 비교하는 함수이다. i의 범위는 0에서 ((NumOf32-1)*2)까지로 equalXY와 KSA가 수행된 횟수를 저장하고 있다. (i%2==0)일땐 KSA 연산으로 두 수의 크기를 비교하고 (i%2==1)일 땐 equalXY 연산으로 두 값의 크기가 같은지 비교한다. com_ic 배열에 KSA와 equalXY 연산의 결과값을 저장하고 KSA와 equalXY 연산이 (1+(NumOf32-1)*2)번 수행되면 com_ic 배열에 저장된 값으로 AND와 OR 연산을 수행한다. j의 범위는 0에서 ((NumOf32-1)*2)까지로 (j%2==0)이고 j가 0보다 클 때, com_ic[j-2] ⊕ (com_ic[j-1] · com_ic[j])의 연산을 수행한다. 연산의 결과 값을 담고 있는 암호문은 비교 연산 마지막에 반환한다.

Fig. 14.

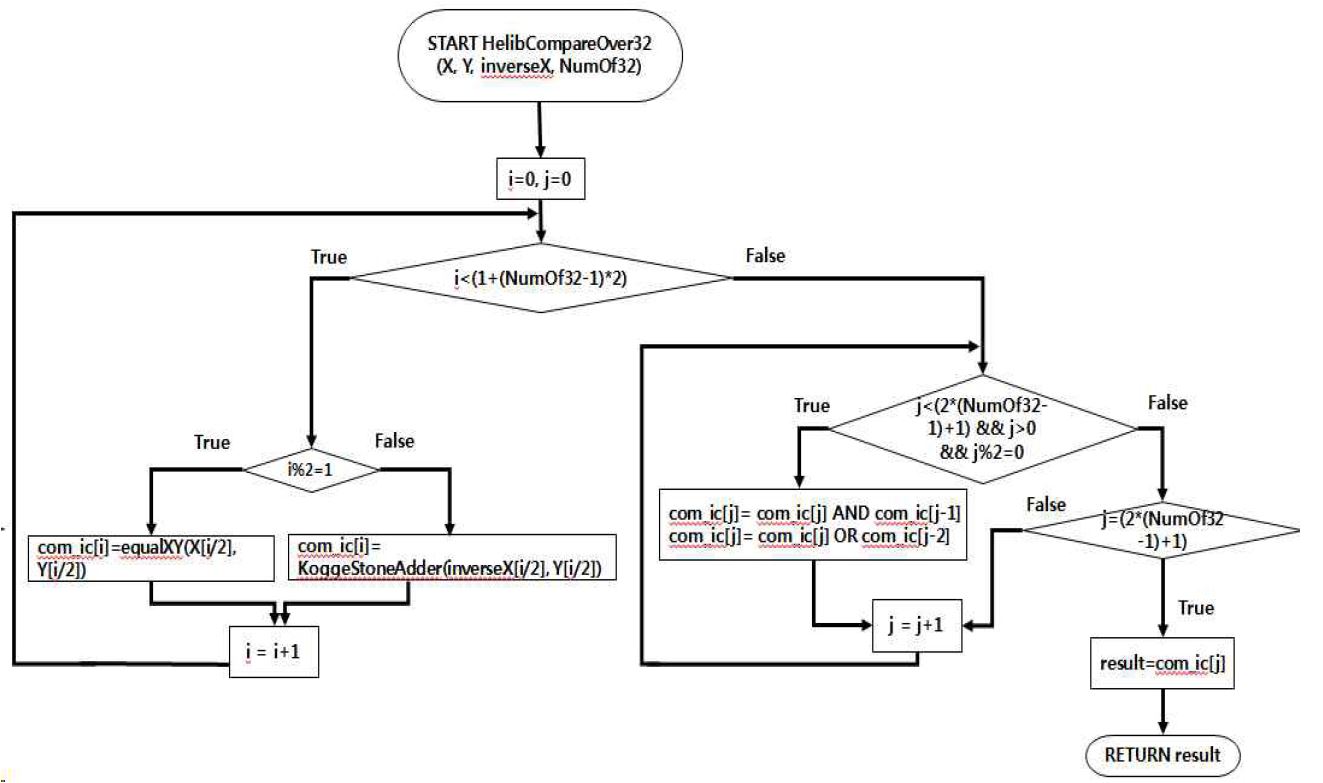
Comparison algorithm for ciphertext over 32bit in HElib (X, Y: An array for storing (NumOf32*32) bit length ciphertexts).

구현 상세: 위 설계에 따라 구현한 소스코드는 아래와 같다.

HElib에서 32bit 이하의 길이 (nb ≤ 32)를 가지는 암호화된 이진수 X와 Y의 크기를 비교하기 위해서는 2³²-1 값을 이진수로 변환한 암호문 ONE과 암호문 X를 기본 제공 XOR 게이트인 addCtxt로 연산을 하여 inverseX를 구한다.

inverseX와 비교할 암호문 Y를 KSA로 가산하여 결과 값은 result_KSA에 저장하여 반환하고 carry 값을 비교 연산의 최종 결과 값으로 반환하기 위해 result에 result_KSA[0] 값을 저장한다. 표 6은 함수의 입력 값과 출력 값을 나타낸다.

Fig. 15.

Pseudocode of comparison operation for ciphertext within 32bit in HElib

Table 6.

Parameters of functions used in HElib

Fig. 16.

Pseudocode of comparison operation for ciphertext over 32bit in HElib

Table 7.

Parameters of functions used in HElib

비교하고자 하는 수의 크기가 32bit보다 클 땐 위의 그림 14의 알고리즘을 따라 비교 연산을 수행한다. 32bit의 단일 암호문 두 개의 숨겨진 평문의 값이 같은지를 비교하는 함수는 equalXY로 구현하였으며 32bit 평문은 NumOf32개로 암호화되어 배열 X, Y에 저장되어 있다. i의 범위는 0에서 1+(NumOf32-1) *2사이로 인덱스 i가 짝수이거나 0이면 암호화된 32bit 이진수 X[i/2]와 2³²-1값을 이진수로 변환한 암호문 ONE과 addCtxt로 XOR 연산한 값을 inverseX에 저장하고, inverseX와 Y로 KSA연산을 수행하여 값의 크기를 비교한다. equalXY와 KSA 연산한 모든 결과는 배열 com_ic에 저장하고 equalXY와 KSA 연산이 종료되었을 때 그림 14의 알고리즘을 따라 계산해준다. 표 7은 함수의 입력값과 출력 값을 나타낸다.

TFHE는 임의의 nb bit의 암호화된 이진수를 배열X[]와 배열 Y[]에 저장한다. 암호화된 이진수 배열X[]와 정수 1을 암호화한 ONE을 XOR 연산하여 배열 inverseX[]에 저장한다. KSA를 통해 inverseX[i]와 Y[i]를 연산한 결과 값을 result_KSA[i]에 저장한다. 최종 비교 결과는 마지막 carry 값인 Y[0]의 값으로 알 수 있다. 표 8은 함수의 입력 값과 출력 값을 나타낸다.

Fig. 17.

Pseudocode of comparison operation for ciphertext in TFHE

Table 8.

Paremeters of functions used in TFHE

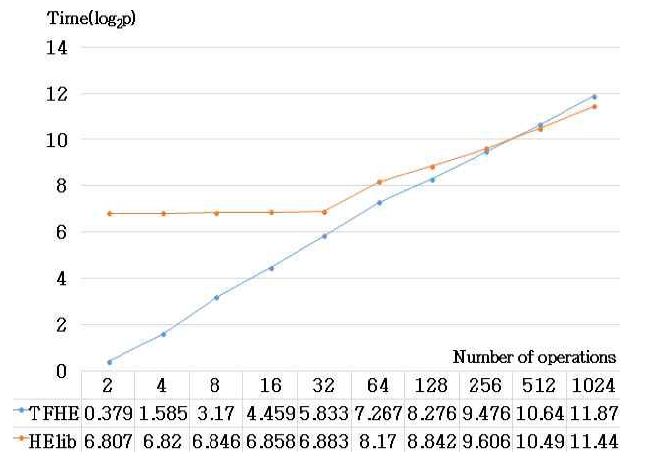
성능 비교: 그림 18은 HElib과 TFHE에서 구현상세를 통해 nb bit의 암호화된 이진수 X와 Y의 비교 연산 수행 시간을 나타낸다.

Fig. 18.

Execution time of comparison operation in HElib and TFHE.

가로축은 비교 연산하는 두 수의 비트를 2에서 1024의 범위로 나타내고, 세로축은 수행 시간(초)을 나타내며 p를 실제 측정된 시간이라고 할 때 log2p로 나타낸다.

HElib은 패킹 기능을 통해 병렬 연산을 수행하기 때문에 비트 수가 증가해도 수행 시간의 차이가 크지 않았다. 그러나 TFHE는 패킹 기능을 제공하지 않아 비트 수가 증가할수록 수행 시간이 증가하는 결과를 보였다. 256bit 이하의 수에서는 TFHE의 비교 연산 수행시간이 더 빠르지만, 256bit 이상으로 비교 숫자들의 비트 수가 증가할 때 HElib이 TFHE보다 빠르게 연산하는 것으로 파악되었다.

구현 상세를 통해 HElib와 TFHE는 비교 연산 알고리즘을 구현할 수 있다는 것을 알 수 있었지만 SEAL은 Noise Budget을 고려할 때 KSA 구현을 통한 비교 연산이 불가능한 것으로 파악되었다.

Ⅳ. 라이브러리의 연산 결과 비교

본 장에서는 3장에서의 덧셈 연산과 비교 연산의 성능 비교를 최종적으로 정리하여 각 라이브러리의 성능을 비교한다. 표 9는 각 라이브러리들의 성능을 비교하기 위해 적용된 파라미터, 연산에 적용된 알고리즘, 연산을 수행한 암호문의 비트 길이와 개수, 그리고 실험 환경을 정리한 표이다.

Table 9.

Overall environment analysis for performance comparison

표 9의 환경을 적용하여 실시한 HElib, TFHE 그리고 SEAL의 32bit와 64bit 길이의 다수 개의 덧셈연산 비교 결과는 그림 6~9에 나타낸다.

3개의 라이브러리는 연산 개수가 증가할수록 수행시간이 선형적으로 증가하였고, 비트 연산이 가능한 HElib과 TFHE에서 덧셈 연산의 수행 시간은 KSA보다 Full Adder 수행 횟수에 영향을 많이 받기 때문에 가산 숫자가 커질수록 두 라이브러리의 실행 시간의 차이가 커진다. 이진수 n개의 덧셈 연산을 수행하였을 때 HElib은 약 (n-2)*t₂+t₁초가 소요될 것으로 예측되고 TFHE는 약 (n-2)*(3*t₂)+t₁/2초가 소요될 것으로 예측되었다.

이를 바탕으로 한 본 실험의 결과로는 6개 이상의 수를 연산할 시에는 HElib의 연산속도가 (-2n+4) *t₂+t1/2초가 빠른 것으로 측정되었다. 십진수 연산을 기본으로 하는 SEAL에서는 HElib 보다 약 1600배 빠른 덧셈 연산이 가능한 것으로 파악되었다.

표 10은 각 라이브러리들의 비교 연산 구현 가능여부를 정리한 표이다.

Table 10.

Available functions for comparison operation in HElib, TFHE and SEAL

비교 연산을 위해 본 논문에서 적용한 KSA는 비트 단위의 연산을 필요로 하며, nb bit의 수를 KSA로 연산할 때 필요한 곱셈 횟수는 1+2log2nb번으로 2bit 연산 시 곱셈 연산을 최소 3회 수행한다. 비트연산이 가능하고 bootstrapping을 지원하는 TFHE와 HElib은 비교 연산이 가능하지만, SEAL에서는 3회 이상 곱셈 연산 수행 시 암호문의 Noise Budget이 0에 도달하게 되고 bootstrapping을 지원하지 않아 암호문의 잡음을 제거할 수 없어 KSA를 이용한 비교 연산이 불가능한 것으로 파악되었다.

Ⅴ. 결 론

본 연구에서는 완전 동형 암호 방법을 지원하는 라이브러리인 HElib, TFHE 그리고 SEAL에서 암호화된 상태에서 산술 연산의 기본 연산인 덧셈 연산과 암호문의 실행 흐름을 제어할 수 있는 비교 연산의 성능을 실제 구현을 통해 비교하였다.

연산의 비교 결과 HElib과 TFHE에서는 덧셈 연산에서 6개 이상의 수를 가산할 때 HElib이 TFHE보다 빠르며 SEAL은 숫자를 비트 단위로 표현하지 않고 수 자체를 암호화해서 사용하기 때문에 HElib보다 1600배 이상 빠른 속도로 덧셈 연산을 수행했다. 비교 연산에서는 HElib과 TFHE는 값의 비교가 가능하며 SEAL에서는 비교 연산을 구현할 수 없는 것으로 파악되었다. HElib과 TFHE는 비트 단위 연산을 지원하여 KSA 연산 결과로 값을 비교할 수 있지만 SEAL은 암호화된 숫자의 부호를 알 수 없기 때문에 비교 연산을 구현할 수 없었다.

비트 연산을 필요로 하는 사용자 중 6개미만의 덧셈을 수행할 경우에는 TFHE의 사용을 제안하고, 6개 이상의 덧셈을 할 경우에는 HElib을 제안한다.

SEAL은 수 자체를 암호화하여 덧셈과 곱셈 연산을 수행하기 때문에 비트 단위로 숫자를 표현하는 다른 라이브러리보다 훨씬 실행 시간이 빠른 장점이 있다. 하지만 허용할 수 있는 잡음의 크기가 제한이 있기 때문에 제한된 수의 곱셈을 효율적으로 수행하는 경우에 사용을 추천한다. 또한 덧셈은 수행횟수에 제한 없이 가능하기 때문에 빠른 덧셈 연산이 필요한 사용자에게 추천한다. SEAL은 빠른 덧셈 연산을 지원하지만 향후 암호화된 상태에서 부호나 절대 값을 알 수 있는 기능에 대한 연구가 필요하며 비트 단위 연산을 지원하게 되면 사용 범위를 넓힐 수 있을 것으로 예상된다.

완전 동형 암호 방식은 암호화된 상태 그대로 연산이 가능하기 때문에 데이터를 외부 유출로부터 보호할 수 있다. 이러한 특징으로 국방, 의료, 금융분야 등에 사용되는 시스템에 적용된다면 유출되어서는 안 되는 군사 기밀 정보, 진료 정보 그리고 금융 정보들의 기밀성 보장뿐만 아니라 기존 암호화 기법보다 빠른 속도로 연산하기 때문에 정보 유출위험이 적으면서도 신속한 서비스 제공이 가능할 것으로 예상 된다[12].

향후 이 연구는 완전 동형 암호화 라이브러리를 사용하는 사용자에게 필요한 기초 자료가 될 것이며 위의 제안한 응용 분야 외에서 이외에도 다양한 분야에도 적용되어 넓은 범위의 대량의 데이터를 안전하게 관리 및 처리에 도움을 줄 것으로 예상된다.

Acknowledgments

이 연구는 서울과학기술대학교 교내연구비 지원으로 수행되었습니다.

References

• KISA, No.2010-23-Password Usage Guide-Convergence Protection R_D Team, (2016).
• IITP, ICT R&D Long-term Technology Roadmap 2022 (Volume 3), (2016).
• HElib, [Online], Available: https://github.com/shaih/HElib/ [Accessed: Aug. 01. 2017].
• I. Chillotti, N. Gama, M. Georgieva, and M. Izabachène, Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds, p3-33, In Asiacrypt (2016). [https://doi.org/10.1007/978-3-662-53887-6_1]
• H. Chen, K. Laine, and R. Player, "Simple Encrypted Arithmetic Library – SEAL v2.1", https://www.microsoft.com/en-us/research/wp-content/uploads/2016/09/sealmanual-2.pdf (2017). [https://doi.org/10.1007/978-3-319-70278-0_1]
• Kyongjin Seo, Pyong Kim, and Younho Lee, "Implementation and Performance Enhancement of Arithmetic Adder for Fully Homomorphic Encrypted Data", Journal of The Korea Institute of Information Security and Cryptology, (2017).
• C. Gentry, S. Halevi, and N. Smart, "Fully homomorphic encryption with polylog overhead", In Advances in Cryptology - EUROCRYPT 2012, volume 7237 of Lecture Notes in Computer Science, p465-482., Springer, (2012), Full version at http://eprint.iacr.org/2011/566. [https://doi.org/10.1007/978-3-642-29011-4_28]
• C. Gentry, A. Sahai, and B. Waters, "Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster", attribute-based. In Crypto 2013, p75-92, (2013).
• Junfeng Fan, and Frederik Vercauteren, Somewhat practical fully homomorphic encryption, Cryptology ePrint Archive Report 2012/144, (2012), http://eprint.iacr.org/.
• Halevi Shai, and Victor Shoup, "Bootstrapping for helib", In Annual International Conference on the Theory and Applications of Cryptographic Techniques, Springer, Berlin, Heidelberg, p641-670, (2015). [https://doi.org/10.1007/978-3-662-46800-5_25]
• TFHE, [Online], Available: https://github.com/tfhe/tfhe [Accessed: Jan. 15. 2018].
• Seung Je Park, and Heeyoul Kim, "Design and Implementation of a Secure Data Storage System for Corporations using Multi-clouds", Journal of Korean Institute of Information Technology, 11(3), p151-157, Mar), (2013. [https://doi.org/10.14801/kiitr.2013.11.3.151]