비공간 애트리뷰트를 포함한 공간 인덱스

2.1 R*-tree

R*-tree는 공간 데이터베이스에서 많이 사용되는 공간 인덱스 중 하나로서 R-tree의 성능을 향상시키기 위해 여러 가지 최적화 기법을 사용한다[1]. 점, 선, 면의 다양한 형태와 크기의 다차원 공간 데이터를 저장 및 관리할 수 있는 효율적인 인덱스 구조이다. 공간 인덱스 R-tree 및 R*-tree는 n개의 축으로 구성된 다차원 공간 데이터를 처리할 수 있도록 설계되었지만, 일반적으로 사용되는 공간 데이터는 x축 및 y축의 (x, y) 기하 좌표를 사용하므로 주로 2차원 데이터를 가지고 인덱스를 구축한다.

본 논문에서 제안하는 NR*-tree는 공간 좌표를 표현하는 기하 2차원 데이터뿐만 아니라 검색에 사용할 수 있는 비공간 데이터도 추가로 포함하여 인덱스를 구축한다.

2.2 비공간 애트리뷰트 활용

공간 데이터는 지도상에 출력되는 모양을 점, 선, 면 형태로 저장하기 위하여 기하 좌표의 값들을 가지고 있고, 해당 공간 데이터의 특성 값을 저장하기 위하여 비공간 애트리뷰트들을 가지고 있다. 비공간 애트리뷰트들은 공간 데이터를 분석하고 활용하는 데 중요한 역할을 담당한다.

다양한 연구들에서 비공간 애트리뷰트를 활용한 인덱스 구조를 제안하고 있다. NSB-tree는 R-tree를 일반적인 비공간 애트리뷰트에 적용하여 제안한 구조이다[2]. Lattice-tree는 R-tree와 Lattice 구조를 혼합하여 공간 위치와 텍스트 키워드와 관계를 조직화하는 구조이다[3]. AR*-tree는 공간 인덱스의 MBR에 MBR의 면적을 포함하여 성능을 향상시킨 구조이다[4].

기하 좌표뿐만 아니라 비공간 애트리뷰트를 같이 분석하는 연구들도 다양하게 수행되고 있다[5][6]. 공간 질의에 비공간 애트리뷰트에 속하는 선호도를 사용하는 연구도 수행되고 있다. 공간적인 위치뿐만 아니라 비공간 애트리뷰트인 선호도에 기반하여 가중치를 할당하여 검색하는 연구[7]와, 선호도를 동맹적 선호도와 적대적 선호도로 나눠서 평가하여 검색하는 연구가 있다[8].

본 논문에서는 공간 인덱스의 질의 처리 성능을 향상시키기 위하여 비공간 애트리뷰트를 활용한 NR*-tree를 제안한다.

3.1 공간 데이터의 기하 좌표 및 MBR

공간 데이터는 기하 좌표의 값과 비공간 애트리뷰트의 값으로 구성된다. 공간 데이터의 기하 좌표 데이터는 타입에 따라서 점 (point), 선 (polyline), 면 (polygon)이 될 수 있다. 점 타입은 일반적으로 2차원 기하 좌표 한 개만 저장하므로 공간 데이터 중에서는 처리가 쉬운 편에 속한다. 반면에 선과 면 타입은 여러 개의 기하 좌표의 값들을 저장하는 가변 길이 데이터로서 구조가 복잡하여 처리하기에 어려움이 따른다.

공간 데이터의 복잡한 기하 좌표들을 처리하기 쉽게 단순화하기 위하여 해당 공간 데이터의 기하 좌표들을 모두 포함하는 가장 작은 사각형인 MBR (Minimum Bounding Rectangle)을 사용한다. 2차원 평면에서 사각형은 (minX, minY) 좌표와 (maxX, maxY) 좌표 두 개만을 사용하여 표현할 수 있다. 공간 인덱스에서는 복잡하고 자세한 공간 데이터의 기하 좌표들 대신에 단순화된 MBR을 사용하여 인덱스를 구축하고 검색에 사용한다.

3.2 비공간 애트리뷰트 저장 방법

기존 R*-tree는 공간 데이터의 MBR을 x축과 y축의 2차원 데이터로 구성하여, 공간 데이터의 효율적인 관리를 제공한다. 제안하는 NR*-tree에서 비공간 애트리뷰트를 MBR에 저장하는 방법은 크게 두 가지로 나뉜다.

3.3 MBR 구조

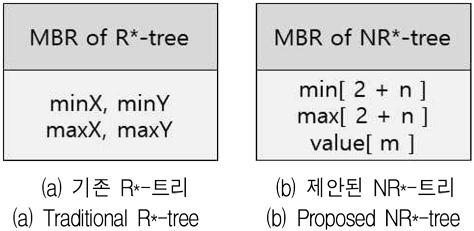
기존 R*-tree에서 2차원 평면상의 공간 데이터를 표현하는 MBR은 그림 1 (a)와 같고, 본 논문에서 제안하는 NR*-tree에서 n개의 수치형 비공간 애트리뷰트와 m개의 카테고리형 비공간 애트리뷰트를 추가로 포함하는 MBR은 그림 1 (b)와 같다.

Fig. 1.

MBR structure

R*-tree에서 2차원 평면상의 공간 데이터를 표현할 때, 본 논문에서 제안하는 NR*-tree에서 MBR의 min[0]과 min[1]은 각각 R*-tree의 minX와 minY에 해당하고, max[0]과 max[1]은 각각 R*-tree의 maxX, maxY에 해당한다.

R*-tree가 다차원 데이터를 처리할 수 있으므로, 제안하는 NR*-tree도 수치형 비공간 애트리뷰트의 범위를 가지고 동일한 알고리즘으로 삽입 및 삭제할 수 있다. m개의 카테고리형 비공간 애트리뷰트는 삽입 및 삭제 알고리즘에서는 사용되지 않는다.

본 논문에서 제안하는 NR*-tree는 기존의 R*-tree에 비공간 애트리뷰트를 포함하여 검색에 사용한다. 검색시 MBR에는 2 + n 차원의 범위를 가지고 있더라도, 질의에서는 2 + n 차원보다 적은 차원의 MBR을 줄 수 있다.

3.4 장축의 길이 활용

본 논문에서 제안하는 NR*-tree에 공간 데이터의 x축 길이와 y축 길이 중에서 길이가 더 긴 장축의 길이를 비공간 애트리뷰트로 MBR에 저장하여 검색에 활용할 수 있다. 장축의 길이는 지도를 출력하기 위해 특정 질의 영역에 속한 공간 데이터를 검색할 때 출력 화면 기준으로 충분히 작은 데이터를 필터링하는 데 사용된다. 충분히 작은 공간 데이터를 필터링함으로써 렌더링 시간은 낮추고 복잡도는 낮춰서 지도의 가독성을 높일 수 있다.

관련 연구에서 살펴본 [4] 연구에서는 공간 데이터의 MBR의 면적을 사용하여 필터링하여 렌더링의 성능을 향상시켰다. 수평선이나 수직선은 면적이 0인 문제점이 있고, 같은 면적을 가지고 있더라도 지도 출력에서는 길이가 더욱 중요한 의미를 가지고 있다. 예를 들어, 면적이 20으로 같을 때, { x축 길이, y축 길이 }가 각각 { 5, 4 }인 경우와 { 20, 1 }인 경우에 지도에서는 길이가 더 긴 { 20, 1 }인 공간 데이터가 출력시 중요도가 더욱 높다. 그러므로, 본 논문에서는 장축의 길이를 비공간 애트리뷰트로 MBR에 추가하여 렌더링 성능과 가독성을 높일 수 있는 방법을 제안한다.

4.1 실험 데이터셋

실험에서 사용된 데이터셋은 국가공간정보포털에서 제공하는 1:5000 축척의 수치지형도 v2.0 데이터 중에서 서울에 해당하는 공간 데이터셋이다. 파일 이름은 “NGII_DTM_V2_5000_서울_강남구.zip”와 같이 서울의 25개 행정자치구에 대해 25개의 압축 파일들로 제공된다. 각 압축 파일에는 해당 구에 포함된 도엽들을 포함한다. 각 도엽은 수치지도 지형지물 표준코드들에 따라 Shape 파일 포맷으로 저장되어 있다. 서울 지역은 총 137개 도엽의 4,512개의 Shape 파일로 구성되며 전체 용량은 1.66GB이다. 전체 공간 데이터는 2,130,239개이다.

실험 데이터셋을 가지고 생성된 R*-tree의 인덱스 파일 크기는 89,758,260 bytes이며, NR*-tree의 인덱스 파일은 128,605,760 bytes이다. 제안하는 NR*-tree는 MBR에 비공간 애트리뷰트의 값들을 포함하고 있으므로 기존 R*-tree보다 43.3% 더 많은 저장 용량을 사용한다. 포함하는 비공간 애트리뷰트가 많아질수록 저장 용량은 증가한다.

본 논문에서 제안하는 NR*-tree의 성능을 평가하기 위해서 공간 인덱스에 포함한 수치형 비공간 애트리뷰트는 MBR의 장축의 길이이고, 카테고리형 비공간 애트리뷰트는 수치지도 지형지물 표준코드이다. NR*-tree의 MBR은 { {minX, maxX}, {minY, maxY}, {minL, maxL}, valueCode } 구조(n=1, m=1)를 갖는다.

4.2 성능 평가

기존의 R*-tree와 본 논문에서 제안한 NR*-tree의 성능을 비교 평가하기 위하여, 서울 전체 수치지도에 대해 정사각형 질의 영역의 길이를 500m, 1Km, 2Km, 4Km, 8Km, 16Km, 32Km로 변경하면서 7개 질의에 대한 검색 시간을 측정한다.

질의 영역에 사용한 수치형 비공간 애트리뷰트는 장축의 길이의 최솟값으로서, 1,000 pixels * 1,000 pixels 이미지로 렌더링할 때 2 pixels에 해당하는 길이를 계산하여 지정한다. 질의 영역에 사용한 카테고리형 비공간 애트리뷰트 값은 교통의 “도로경계(미분류)”, “교량”, “교차로”, “입체교차부”, “인터체인지”, 모든 건물, 모든 시설, 수계의 “하천경계”, “호수/저수지”, 지형의 등고선 중에서 “계곡선”이다.

랜덤 함수를 사용하여 임의로 100개의 질의 영역을 생성하여 검색 시간을 측정하고 평균을 계산한다. 실험 환경은 AMD Ryzen9 3900X 12-Core 3.80GHz CPU, 32GB 메모리, Windows 10 Pro. 운영체제를 사용하였다. 표 1은 실험 결과를 보여준다.

Table 1.

Experimental results for search time (ms)

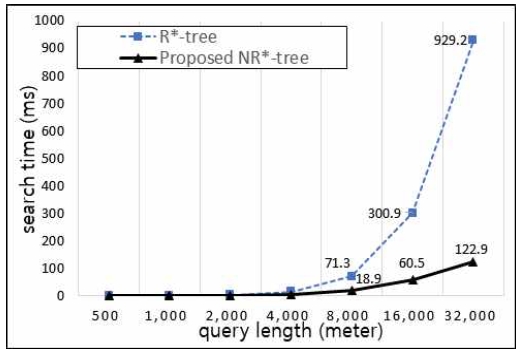
NR*-tree는 R*-tree에 비해 500m에서는 70.6%, 32Km에서는 13.2%의 시간만으로 검색할 수 있어서 우수한 성능을 보여준다. 표 1의 실험 결과를 그래프로 표현하면 그림 2와 같다.

Fig. 2.

Performance evaluation graph

그림 2에서 보는 바와 같이 기존의 R*-tree과 비교하여 제안한 NR*-tree의 성능은 질의 영역이 커질수록 더욱 우수한 성능을 발휘함을 알 수 있다.

4.3 NR*-tree 장축 필터링

그림 3은 정사각형 질의 영역의 길이가 8Km인 경우에 장축의 길이를 적용하지 않을 때(a)와 화면상에서 각각 2, 4, 8 pixels에 해당하는 장축의 길이를 적용했을 때의 1,000 pixels * 1,000 pixels 결과 이미지를 보여준다.

Fig. 3.

Major axis filtering results

장축의 길이가 2 pixels보다 작은 MBR을 검색 결과에서 필터링한 그림 3 (b)와 4 pixels로 필터링한 그림 3 (c)는 장축의 길이를 적용하지 않은 그림 3 (a)에 비해 상세함이 부족하지 않고 오히려 가독성이 높은 결과를 보여준다. 검색에 소요되는 시간도 약 20% 정도씩 줄어든다. 8 pixels로 필터링한 그림 3 (d)는 다소 상세함이 부족하긴 하지만, 2 pixels로 필터링한 검색 시간보다 약 40% 정도 감소하므로 필요에 따라 사용할 수도 있다.