다중 로봇 커버리지 경로 계획을 위한 유전 알고리즘과 개미 집단 최적화 방법의 조합 성능에 관한 연구
초록
본 연구에서는 다중 로봇 커버리지 경로 계획(MCPP, Multi-robot Coverage Path Planning)을 위해 대표적인 휴리스틱(Heuristic) 기법인 유전 알고리즘(GA, Genetic Algorithm)과 개미 집단 최적화(ACO, Ant Colony Optimization)의 특징을 토대로 이들의 다양한 조합에 대한 성능 비교 연구결과를 보였다. 이를 위해, 환경, 노드 개수, 경로 생성, 수행 시간의 측면에서 ACO와 GA의 개별 특징을 분석하였다. 개별 특징을 토대로 MCPP를 위해 4가지의 ACO와 GA의 조합 구조가 선정되었고, 다양한 환경에서 이 조합 구조들이 테스트되었다. 테스트 결과로부터 각 구조의 수렴시간 및 경로 Cost 결과가 비교 분석되었다. 향후에는 이 분석 결과를 토대로 주어진 환경에 가장 적합한 MCPP 구조를 제안하는 연구를 진행할 계획이다.
Abstract
In this study, we aim to compare the performance of various combinations of genetic algorithm(GA) and ant colony optimization(ACO) which are two representative heuristic algorithms for multi-robot coverage path planning (MCPP). First off, we analyze the individual characteristics of ACO and GA in terms of environments, the number of nodes, the quality of the generated paths, and execution time. We construct four combinations of ACO and GA for MCPP and perform them in several environments. Subsequently, we compare and analyze them accroding to the convergence time and path cost of each combination. In the future, we plan to propose an MCPP structure that is most suitable for a given environment based on these analysis results.
Keywords:
ant colony optimization, genetic algorithm, multi-robot coverage path planning, hierarchical structureⅠ. 서 론
최근 무인 대공간(Unmanned large space) 감시(Surveillance), 청소(Cleaning), 잔디 깎기(Lawn mowing), 크레바스 탐사(Crevasse exploration) 등과 같은 다양한 목적을 위해 다중 로봇 커버리지 경로 계획(MCPP, Multi-robot Coverage Path Planning)에 대한 연구가 활발히 진행되고 있다[1]-[5]. 이 중 청소와 잔디 깎기와 같은 임무는 MCPP 문제에서 로봇에 탑재된 센서의 탐지 거리와 무관하게 주어진 영역을 Boustrophedon Decomposition[6]의 형태로 방문해야한다. 하지만, 감시, 탐사와 같은 문제는 다중 로봇이 제한된 시간 내에 센서의 탐지 거리(SR, Sensing Range)를 기반으로 주어진 영역을 완전히 감시 및 탐사함을 목표로 한다. 본 연구에서도 주어진 환경에서 SR를 기반으로 생성된 방문 지점(Viewpoints)에 대해 최적의 MCPP가 수행되어 다중 로봇의 방문 경로를 생성하는 것을 다룬다.
일반적인 경로 계획 (PP, Path Planning)은 한 점에서 다른 한 점으로 로봇이 이동하기 위해 장애물과 충돌하지 않는 안전한 경로를 계획하는 과정을 의미한다[7]. 만약, 로봇이 탑재된 센서를 이용하여 주어진 전체 영역을 커버리지하는 경우 SR를 기반으로 방문 지점이 생성되고, 각 지점이 모두 방문되도록 PP를 수행할 수 있다. 이때, 모든 방문 지점을 최소의 비용으로 방문하는 문제를 외판원 문제(TSP, Traveling Salesman Problem)로 정의한다. 커버리지 경로 계획(CPP, Coverage Path Planning)은 이러한 일련의 과정을 의미한다[8]. 다중 로봇 커버리지 경로 계획인 MCPP는 CPP를 다중 로봇에 대한 문제로 확장한 것을 의미한다. MCPP는 경로 기반 접근법(Path based Approach)과 영역 기반 접근법(Area based Approach)으로 나뉘어진다[9]. 경로 기반 접근은 다중 외판원 문제(mTSP, multiple TSP) 문제로, CPP의 수행결과를 m대의 로봇에 균일하게 나누어 할당하는 방법을 의미한다. 영역 기반 접근은 먼저 전체 영역을 로봇 대수인 m만큼 나눈후 각 영역에 대해 단일 로봇 CPP를 수행하는 것을 의미한다. 본 연구에는 다중 로봇 경로의 효율성 문제에 집중하기 위해 경로 기반 접근법 구조에 대해 다룬다.
경로 기반 접근법에서 방문 지점(노드)과 그 사이 거리 정보(엣지)는 그래프로 표현된다. 따라서, CPP의 핵심은 그래프로 표현된 영역의 최적 경로를 찾는 것이다. 하지만, 대부분의 TSP는 NP-hard 문제이다. 따라서 이를 풀기위해 휴리스틱(Heuristic) 방법이 필요하다[10]. 대표적인 방법으로 유전 알고리즘(GA, Genetic Algorithm)[11]과 개미 군집 최적화(ACO, Ant Colony Optimization) 방법[12]이 있다. 각 방법은 단일 로봇의 CPP를 풀기 위해 주로 활용되었지만, 본 연구에서는 MCPP를 위해 이 두 방법의 4가지 조합 구조를 제시(GA-GA, GA-ACO, ACO-GA, ACO-ACO)하고, 환경(엣지의 형태) 및 방문 지점(노드 개수)에 변화에 따른 성능을 비교한다.
따라서 본 논문의 기여도는 다음과 같다.
1. MCPP를 위한 계층화(Hierarchical)된 GA와 ACO 방법의 조합 구조 제시
2. 수렴속도와 수렴결과(MCPP 결과)에 따른 GA와 ACO 방법 조합 구조 성능 분석
본 논문의 구성은 다음과 같다. 2장은 MCPP와 관련된 다양한 연구를 소개한다. 3장에서는 단일로봇 CPP 문제를 풀기 위한 GA와 ACO 방법 및 특징이 설명된다. 4장은 MCPP를 위한 GA와 ACO 방법의 다양한 조합 구조를 제시한다. 5장은 CPP 문제에 대한 GA와 ACO 방법의 실험을 수행하고 특성을 분석하며, MCPP 문제에 대한 GA와 ACO 방법의 다양한 조합 구조의 성능 비교 실험을 수행한다. 이때, 실험 환경에 따른 각 구조의 수렴속도와 수렴결과 분석이 함께 진행된다. 마지막으로 6장에서는 결론에 관해 기술하고, 향후 연구 방향에 대해 제시한다.
Ⅱ. 관련 연구
소독로봇[13], 수확로봇[14], 진공청소로봇[15], 감시로봇[3] 등 다양한 분야에서 CPP에 관한 연구들이 이루어지고 있다. 그들의 연구는 주로 커버리지 완전성(Completeness)과 커버리지 경로의 중복 최소화(Minimizing overlap of coverage paths)에 관한 것이다[16]-[18].
CPP 연구 중 MCPP 연구는 다중로봇을 다룬다는 점에서 도전적인 문제이다[19]. 그러나 단일로봇 CPP에 비해 MCPP는 작업을 병렬로 완료하고, 시간 소모 감소 및 효율성 향상 등 다양한 장점이 있다.
MCPP 연구의 핵심은 mTSP를 푸는 방법에 있다. MCPP 연구는 경로 기반 접근과 영역 기반 접근으로 나눌 수 있다[9]. 영역 기반 접근을 위한 방법으로는 Lloyd 알고리즘[20], 보로노이 분할(Voronoi partitioning)[21], K-means[22], 휴리스틱 기법[23] 및 대체 제안 프로토콜(Alternate-offer protocol)[24] 등이 있다. 각각은 개별 특성이 있는 방법들이지만, 영역 분배에 있어 최적이 아닌 결과를 주어 최적의 MCPP 결과를 얻는 데 어려움이 있었다. 그 중 DARP(Divide Areas based on Robots initial Positions) 방법[25]은 격자 지도가 주어졌을 때 로봇 최기값과 장애물을 토대로 각 로봇에 최적 영역을 할당하는 방법이다. 이 방법은 Spanning Tree와 ACO가 결합된 형태로 연구가 진행되기도 하였다. 하지만 경로 생성 전 영역 분배는 계산량 감소에는 큰 도움을 주지만, MCPP의 최적해 도출에는 어려움이 있다.
경로 기반 접근법 중 대표적인 연구는 [26][27]에서 소개되었다. 해당 연구에서는 Klee에 의해 작성된 아트 갤러리 문제(AGP, Art Gallery Problem)를 토대로 진행되었다[28]. AGP는 아트갤러리를 지키기 위해 센싱 범위를 가지는 필요한 최소한의 고정가드를 두는 문제이다. 해당 연구에서는 고정가드를 두는 문제를 필수로 방문해야 하는 노드(Viewpoints) 생성하는 문제로 보았다. 이렇게 생성된 노드를 기반으로 그래프를 완성하고, 클러스터 기반 알고리즘과 순환 커버리지 방법들을 사용하여 MCPP를 수행하였다. [3]에서는 MCPP를 위해 위 연구를 향상 및 확장하였다. 방문해야하는 노드는 주어진 지도의 노멀 벡터(Normal vector) 방향으로 SR를 고려하여 생성하였다. 또한, 균일한 경로를 얻기 위해 (Balanced path) 경로 분할, 재병합 등의 과정이 추가되었다. 본 연구에서는 [3]의 그래프 구성 방법을 활용한다. 대신, 최근접 이웃 탐색(Nearest neighbor) 기반의 TSP 접근법 대신 휴리스틱한 다양한 구조(ACO-ACO, ACO-GA, GA-GA, GA-ACO)를 제시하고 성능을 비교한다.
Harrath 등[29]은 ACO, two-opt, GA를 이용한 하이브리드 방법론을 제안했다. ACO는 TSP문제를 푸는 솔루션으로 활용했으며, two-opt 알고리즘과 GA는 해당 솔루션을 향상하기 위해 활용되었다. 본 연구와 유사한 이중 구조이지만, 다양한 휴리스틱 구조에 대한 분석은 없었다.
Ⅲ. GA와 ACO 기반 CPP 접근법
CPP문제를 해결을 위해 먼저 그래프 G의 구축이 필요하다. 그래프의 노드 N는 [3]의 연구를 토대로 주어진 지도의 점유(Occupied)지역에서 노멀벡터 방향으로 SR를 고려하여 생성된다. 엣지 E는 두 노드가 지도의 자유공간을 따라 연결된다면, 값을 가지게 되고 그 값은 Euclidean Distance로 계산된다. 구축된 그래프로부터 우리가 풀고자 하는 문제는 다음과 같다[30].
| (1) |
| (2) |
| (3) |
xij는 서로다른 i, j에 대해 연결여부(xij∈0,1)를 의미한다.
그래프가 구성되었을 때, GA 기반 CPP는 다음과 같은 방법으로 진행된다. 초기 경로(염색체) P1과 P2가 주어진다면, 교배가 수행된다(교배율: RCross). 이 때 진화(Evolution)의 방향은 경로 Cost가 감소하는 방향으로 진행되고, 경로의 Cost는 그래프 엣지의 합으로 계산된다. GA는 Local Minima 문제를 해결하기위해 확률 RMu로 돌연변이가 수행된다. 또한, 병렬 연산을 위한 염색체의 개수 mch도 사전에 정의되어 활용된다. 본 연구에서는 이러한 파라미터를 [31]의 연구를 기반으로 진행하였다.
ACO 기반 CPP는 다음과 같은 방법으로 진행된다. 먼저, 구축된 그래프에서 mant 개미들이 초기화 규칙에 따라 무작위로 노드를 선택한다.
각 개미들은 상태전이규칙(State transition rule)에 따라 다음에 방문할 노드를 선택하고, 반복적인 탐색과정을 거친다. 이러한 과정을 거치는 동안 개미들은 지역 갱신 규칙(Local updating rule)에 따라 방문한 각 노드에 페로몬 양을 갱신한다. 이러한 방법을 반복한 후, 모든 개미들의 탐색과정이 종료되면 전역 갱신 규칙(Global updating rule)에 따라 다시 페로몬 양이 갱신된다. 갱신 시에는 α(Pheromone coefficient), β(Heuristic coefficient), ρ(Pheromone’s evaporation rate)와 같은 파라미터에 의해 갱신의 양이 결정된다. 결국, 각 개미들은 가까운 노드를 선택하려는 휴리스틱 정보와 많은 양의 페로몬을 가진 노드를 선택하려는 페로몬 정보에 따라 탐색 경로를 완성한다. 이러한 과정을 Iteration 횟수 만큼 반복하는 구조이다.
[12]는 ACO를 TSP에 적용하였을 때 변수의 변화에 따른 성능 분석을 다룬 연구로, 본 연구의 실험파트에서도 해당 연구의 분석 결과를 활용하였다.
Ⅳ. MCPP 구조
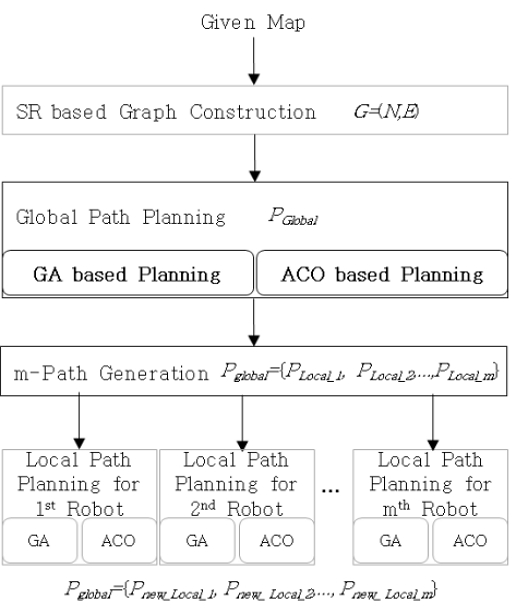
그림 1은 제안한 MCPP 구조에 대한 시스템 순서도이다. 지도가 주어졌을 때, SR 기반의 그래프 G가 구축된다. 주어진 그래프의 노드를 따라 전역 경로 계획을 수행한다. 이때 GA 또는 ACO가 활용된다. 생성된 전역 경로 PGlobal는 주어진 로봇의 대수 m만큼 균등히 나눌 수 있다(PGlobal={PLocal_1, PLocal_2,...,PLocal_m}). 각 나누어진 경로에 대해 다시 GA 또는 ACO가 수행되어 개별 최적 로봇의 경로(Pglobal={Pnew_Local_1, Pnew_ Local_2,..., Pnew_ Local_m})가 얻어진다. 따라서 전역 경로 계획과 지역 경로 계획을 위한 방법론에 따라 ACO-ACO, ACO-GA, GA-GA, GA-ACO 총 4가지 구조가 가능하다.
MCPP 문제에서는 많은 노드로 인해 전역 경로 생성 과정이 최적임을 가정할 수 없다(즉, Local Minima 가능성 존재). 하지만 지역 경로 계획에서는 전체 노드에서 로봇 대수 m만큼 나눠진 노드 개수이므로 최적의 경로를 생성할 가능성이 높다. 따라서 계층적인 형태의 MCPP 방법이 전역 경로 생성만 이용한 방법에 비해 최적에 가깝다.
Ⅴ. 실 험
실험하기에 앞서 우리는 각 알고리즘에 적용할 파라미터 값을 표 1에 나타내었다.
실험환경에 적용될 지도의 크기는 모두 동일한 4706×3968pixel (실제 약 수 km – 수십 km 사이 환경) 이다. 본 연구에서는 지형의 복잡성에 따라 3가지 종류의 지도가 정해졌다. 각 환경이 선택된 이유와 알고리즘 특성에 따른 실험 예상 결과는 다음과 같다.
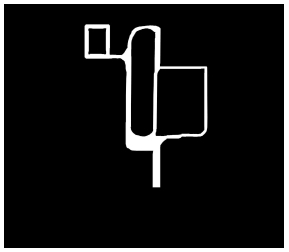
백지 환경은 그림 2와 같이 장애물이 없는 간단한 환경이기 때문에 생성된 노드 간의 연결성이 강하게 나타난다(Strong connection). 이는 경로 선택 시 노드 선택에 따른 차이가 크지 않다. 즉, 임의의 위치에서 최적 노드 선택에 실패하더라도 유사한 경로가 선택될 가능성이 크다.
부분적으로 복잡한 환경의 경우, 그림 3(a) 지도와 같이 전체 환경이 일부 지역에 가로막혀 있는 환경이다. 그림 3(b)의 흰색영역은 로봇이 이동할 수 있는 영역이고, 검은색 영역은 이동이 불가능한 영역이다. 따라서 가로막힌 영역에 의해 그래프 구축 시 엣지에 대한 추가적인 계산 시간이 필요하다. 또한, 백지 환경보다 부분적으로 노드와 노드 사이 연결성이 높지 않으며, 이로 인해 알고리즘의 CPP 수행 결과가 다소 차이 날 가능성이 있다. 즉, ACO와 GA가 적용되면, 환경 내 분기가 일어나는 지점에서 페로몬의 양과 같은 정보를 줄 수 있는 ACO가 GA보다 더 좋은 수행 결과를 줄 수 있다.
복잡한 환경의 경우, 그림 4에 제시된 지도로, 분기가 많은 형태(흰색을 통해 이동)로 되어있다. 따라서 그래프 구축 시 연결 여부 판단에 시간이 많이 소요되고, 노드와 노드 사이 연결성이 약하다(Weak connection). 이 환경에서 그래프 구축 후 ACO와 GA의 성능을 측정한다면, 환경 내 많은 분기로 인해 페로몬의 양과 같은 정보를 줄 수 있는 ACO가 GA에 비해 좋은 결과를 낼 수 있다.
5.1 ACO와 GA 기반 CPP 실험 및 결과 분석
GA와 ACO를 적용하여 CPP를 수행할 때 경유해야 하는 노드의 수, 지도의 장애물 배치 정도에 따른 거리와 수행시간을 비교하기 위해 서로 다른 지형으로 구성된 3종류의 지도에서 각 알고리즘이 테스트 되었다. 각 알고리즘에서 성능지표에 사용된 평균 이동 길이 Lavg는 다음의 수식을 통해 계산된다.
| (4) |
M은 반복 실험 횟수를 의미하고 각 실험은 10회씩 진행되었다. N은 생성된 PGlobal의 크기를 의미한다.
백지 환경의 경우, 실험 결과는 표 2와 같이 나타났다. 노드의 수가 43개와 104개일 경우, GA가 ACO에 비해 더 작은 Lavg를 보인다.
이는 GA가 ACO에 비해 더 최적에 가까운 경로를 생성함을 의미한다. 노드의 수가 212개일 때의 실험 결과에서 ACO는 30초까지 수행시간이 경과 했을 때 좋은 경로를 찾지 못했으나 60초의 수행시간이 경과 했을 때 GA보다 Lavg가 낮은 경로를 생성하였다. 이러한 결과형태가 나타나는 이유는 ACO의 구조가 페로몬 정보의 축적과 갱신을 통해 최적의 경로로 수렴하기 때문에 수행시간이 30초 이하로 주어졌을 경우 페로몬 정보가 부족하여 비효율적인 결과가 나타나고, 페로몬 정보가 충분히 확보되었을 때 효율적인 경로 결과가 나오기 때문이다.
부분적으로 복잡한 환경의 실험 결과는 표 3에 기술되었다. 해당 실험의 경우, 노드 수가 많지 않을 때(16개) 이른 수렴을 통해 GA가 ACO에 비해 Lavg기준으로 189만큼 좋은 성능을 나타내었다.
또한, 표 2의 실험 결과와 유사하게 노드의 수가 많고(168개), 수행시간이 충분하지 않을 경우(10초) ACO는 GA에 비해 Lavg기준으로 성능이 좋지 않다. 반면 충분한 수행 시간이 주어졌을 경우(30초), ACO가 GA보다 효율적인 경로를 생성하였다.
분기가 많은 형태로 구성된 복잡한 환경에서 진행된 실험 결과는 표 4와 같다. 표의 실험 결과를 보면, 부분적으로 복잡한 환경에서 실험한 결과와 유사한 형태의 결과가 나타난다. 특히, 마지막 실험 결과에서 표 3에 나타난 실험 결과의 경우, ACO가 GA보다 약 5,845 만큼(ACO:58,984, GA:64,894) 단축된 Lavg값을 가졌었는데, 복잡한 환경에서 더 적은 노드(113개)에 대해 ACO가 GA보다 70,221 만큼(ACO:22,314, GA:90,490) 단축됨을 보였다. 이것은 환경 복잡도에 따라 두 알고리즘의 성능 차이를 보여준다.
GA의 경우 노드의 수가 50개 이하이거나, 장애물이 없는 단순한 구조의 지형에서 거리와 시간의 효율을 종합해서 볼 때 ACO보다 좋은 성능을 보였다. ACO는 노드 수가 많고, 복잡한 환경일수록 충분한 수행 시간(30초이상)이 주어진다면 GA보다 높은 최적화 성능이 나타난다. 이처럼 CPP가 적용될 지형 및 노드의 수에 따라 각 알고리즘의 성능 차이가 있었다. 이러한 ACO와 GA의 특정 조건에 대한 강점을 활용하여 다음 장에서는 두 조합의 다양한 계층적인 구조를 실험을 통해 분석하고, 환경 구조에 따른 효율적인 알고리즘을 알아보고자 한다.
5.2 MCPP에 대한 다양한 ACO GA 조합 구조의 특성 분석
MCPP 실험에서는 총 6가지 구조가 활용되었다. 단일 구조의 Single-ACO, Single-GA와 계층구조의 ACO-ACO, ACO-GA, GA-GA, GA-ACO 이다. 각 GA와 ACO 알고리즘은 추정 경로가 수렴될 때까지 수행되었다(생성된 경로의 변화가 ε 이하가 되면 수렴으로 판단). 모든 실험환경에서 MCPP를 위한 로봇 대수 m은 3으로 정해두었다. 각 구조에서 성능지표에 사용된 MCPP 결과의 평균 이동 경로의 길이 MLavg는 다음의 수식을 통해 계산된다.
| (5) |
M은 총 실험 횟수를 의미하고, m은 로봇의 대수를 의미한다. N(k)은 k번째 로봇의 생성된 PLocal의 크기를 의미한다.
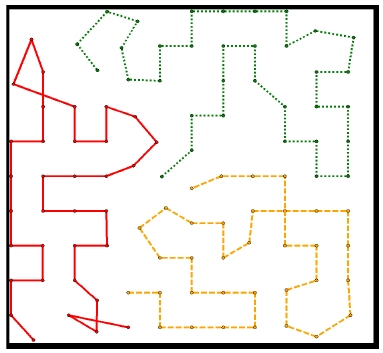
백지 환경 실험은 GA와 ACO의 성능이 각각 적절히 나타난 104개 노드 수에 대해 진행되었다. 결과는 표 5에 나타내었다. ACO-GA의 MLavg가 41,631로 가장 최적에 가까운 이동 경로를 생성하였다. 수행시간이 가장 빠른 알고리즘은 Single-GA로 ACO-GA 구조와 비교했을 때 MLavg이 5,352 증가했으나 수행시간에서 50.97초 단축된 결과를 보였다.
그림 5는 백지 환경에서 수행한 알고리즘 구조 중 가장 좋은 이동 경로를 생성한 ACO-GA의 실험 결과이다.
부분적으로 복잡한 환경에 대한 실험도 앞선 5.1장에서 진행된 실험 중 적절한 노드 개수(51개)가 생성된 경우에 대해 실험을 진행하였다. 표 6은 부분적으로 복잡한 환경에서 수행한 실험 결과다.
성능 비교를 통해, MLavg이 제일 낮게 나오는 구조는 ACO-GA이다. ACO-ACO의 경우, ACO-GA 구조를 제외한 다른 알고리즘 구조들보다 비교적 낮은 MLavg를 보였지만, 소요 시간이 15.17초로, ACO-GA보다 5.08초 더 소요되었다.
수행시간이 가장 짧은 알고리즘은 Single-GA로 수행시간이 짧지만 MLavg가 ACO-GA보다 10,521만큼 길게 나오므로 거리와 시간 정보를 종합해서 볼 때 효율적이지 않은 선택으로 볼 수 있다. 그림 6은 MLavg가 가장 낮은 ACO-GA구조의 실험 결과이다.
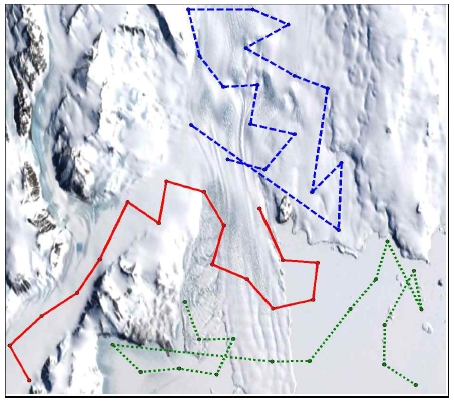
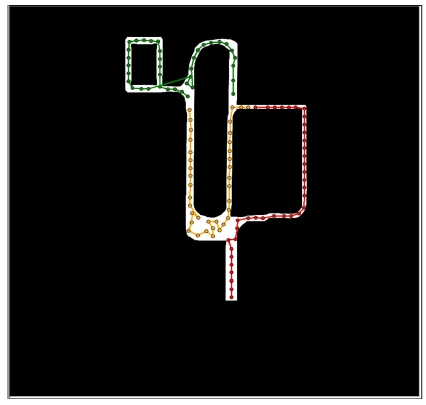
복잡한 환경의 실험은 전체 노드의 수를 113개로 두고 진행되었다. 표 7는 알고리즘 비교 실험 결과이다. MLavg가 가장 짧은 구조는 ACO-GA로, 수행시간은 전체의 평균시간인 46.05초와 유사한 49.74초가 측정되었다. 수행시간이 가장 빠른 구조는 Single-GA로 11.38초의 수행시간을 가졌다. 이는 ACO-GA보다 38.36초 빠른 수치이다.
하지만, 거리를 비교했을 때 Single-GA의 MLavg가 ACO-GA보다 66,629만큼 크게 나와 평균 이동 거리 관점에서 다른 방법에 비해 좋지 않은 성능을 보였다. ACO-ACO의 경우, ACO-GA와 비슷한 경로 생성 결과를 가졌지만, 수행시간이 105.31초로 약 2배 이상 오래 걸렸다. 그림 7은 거리 측면에서 가장 좋은 성능을 보여준 ACO-GA구조의 실험 결과이다.
백지 환경의 경우, Single-GA와 GA-GA는 전체 방법들의 평균에 못 미치는 MLavg값을 가졌지만 빠른 수행시간을 보였다. ACO-GA의 경우, 가장 최적에 가까운 거리 생성 결과를 보였지만, 상대적으로 긴 수행시간을 보였다. 부분적으로 복잡한 환경의 경우, Single-GA와 GA-GA는 수행시간의 성능은 우수하나 분기점으로 인해 GA 성능이 좋지않아 상대적으로 긴 경로를 생성하였다. 반면, ACO-GA의 경우 가장 짧은 최적화 경로와 평균에 가까운 수행시간을 보였다. 따라서 수행시간 대비 생성된 경로의 길이면에서 가장 효율적인 성능을 가지는 구조는 ACO-GA이다. 복잡한 환경일 경우, 부분적으로 복잡한 환경에서 테스트한 결과와 유사한 결과가 나타났다. 특히, ACO-GA의 효율성이 극대화되었다. 위의 결과에 대한 분석내용을 토대로 주어진 지도와 환경 조건에 따라 적절한 ACO, GA 계층 구조를 만들 수 있고, 최종적으로 거리와 시간적으로 단축된 MCPP 결과를 얻을 수 있다.
Ⅵ. 결론 및 향후 과제
본 연구에서는 MCPP를 위해 대표적인 휴리스틱 기법인 GA와 ACO의 개별 특징을 분석하고, 이들의 다양한 계층적 조합(GA-GA, GA-ACO, ACO-GA, ACO-ACO)을 제시하였다. 또한, 다양한 환경에서 이러한 조합들이 생성한 경로의 길이와 수행시간이 측정되었다. 측정 결과를 바탕으로 환경에 따른 각 계층구조의 특징이 분석되었다. 향후에는 이 분석 결과를 토대로 주어진 환경에 가장 적합한 MCPP 구조를 제안하는 연구를 진행할 예정이다.
Acknowledgments
이 연구는 금오공과대학교 학술연구비로 지원되었음(202001770001)
References
-
T. Alam and L. Bobadilla, "Multi-Robot Coverage and Persistent Monitoring in Sensing-Constrained Environments", Robotics, Vol. 9, No. 2, pp. 1-18, Jun. 2020.
[https://doi.org/10.3390/robotics9020047]

-
J. Scherer and B. Rinner, "Multi-Robot Patrolling with Sensing Idleness and Data Delay Objectives", Journal of Intelligent & Robotic Systems, Vol. 99, pp. 949-967, Mar. 2020.
[https://doi.org/10.1007/s10846-020-01156-6]

-
D. Noh, J. Choi, J. Choi, D. Byun, K. Youngjae, H. R. Kim, S. Baek, S. Lee, and H. Myung, "MASS: Multi-Agent Scheduling System for Intelligent Surveillance", 19th International Conference on Ubiquitous Robots(UR), Jeju, Korea, pp. 252-257, Jul. 2022.
[https://doi.org/10.1109/UR55393.2022.9826281]

-
S. H. Lee, "A New Entrapment Based Invader Capture Strategy for Multi-robot Surveillance Systems", IntelliSys 2022: Intelligent Systems and Applications, Vol. 543, pp. 318-327, Sep. 2022.
[https://doi.org/10.1007/978-3-031-16078-3_20]

-
S. H. Lee, "A Multi-Robot Balanced Coverage Path Planning Strategy for Patrol Missions", 21st International Conference on Control, Automation and Systems(ICCAS), Jeju, Korea, pp. 1567-1569, Oct. 2021.
[https://doi.org/10.23919/ICCAS52745.2021.9649836]

-
H. Choset, "Coverage of Known Spaces: The Boustrophedon Cellular Decomposition", Autonomous Robots, Vol. 9, pp. 247-253, Dec. 2000.
[https://doi.org/10.1023/A:1008958800904]

-
H. Wang, S. Lou, J. Jing, Y. Wang, W. Liu, and T. Liu, "The EBS-A* algorithm: An improved A* algorithm for path planning", PLoS One, Vol. 17, No. 2, Feb. 2022.
[https://doi.org/10.1371/journal.pone.0263841]

-
X. Huang, M. Sun, H. Zhou, and S. Liu, "A Multi-Robot Coverage Path Planning Algorithm for the Environment With Multiple Land Cover Types", IEEE Access, Vol. 8, pp. 198101-198117, Sep. 2020.
[https://doi.org/10.1109/ACCESS.2020.3027422]

-
C. Gao, Y. Kou, Z. Li, A. Xu, Y. Li, and Y. Chang, "Optimal Multirobot Coverage Path Planning: Ideal-Shaped Spanning Tree", Hindawi, pp. 1-11, Sep. 2018.
[https://doi.org/10.1155/2018/3436429]

- C. H. Yi and D. W. Kim, "Comparisons of Robot-Moving Strategies with Evolutionary Algorithm and Neuro-Fuzzy Method", Journal of KIIT, Vol. 10, No. 2, pp. 227-232, Feb. 2012.
-
S. A. Haroun, B. Jamal, and E. H. Hicham, "A Performance Comparison of GA and ACO Applied to TSP", International Journal of Computer Applications, Vol. 117, No. 19, pp. 28-35, May 2015.
[https://doi.org/10.5120/20674-3466]

- D. Asmar, A. Elshamli, and S. Areibi, "A Comparative Assessment of ACO Algorithms Within a TSP Environment", Dynamics of Continuous, Discrete and Impulsive Systems Series B: Applications and Algorithms, Jul. 2005.
-
B. Nasirian, M. Mehrandezh, and F. Janabi-Sharifi, "Efficient Coverage Path Planning for Mobile Disinfecting Robots Using Graph-Based Representation of Environment", Frontiers Robot. AI, Vol. 8, Mar. 2021.
[https://doi.org/10.3389/frobt.2021.624333]

-
M. M. Rahman, K. Ishii, and N. Noguchi, "Optimum harvesting area of convex and concave polygon field for path planning of robot combine harvester", Intelligent Service Robotics, Vol. 12, No. 2, pp. 167-179, Feb. 2019.
[https://doi.org/10.1007/s11370-018-00273-4]

-
X. Miao, H. S. Lee, and B. Y. Kang, "Multi-Cleaning Robots Using Cleaning Distribution Method Based on Map Decomposition in Large Environments", IEEE Access, Vol. 8, pp. 97873-97889, May 2020.
[https://doi.org/10.1109/ACCESS.2020.2997095]

-
S. Chakraborty, D. Elangovan, P. L. Govindarajan, M. F. Elnaggar, M. M. Alrashed, and S. Kamel, "A Comprehensive Review of Path Planning for Agricultural Ground Robots", Sustainability, Vol. 14, No. 15, pp. 9156, Jul. 2022.
[https://doi.org/10.3390/su14159156]

-
E. Galceran and M. Carreras, "A survey on coverage path planning for robotics", Robotics and Autonomous Systems, Vol. 61, No. 12, pp. 1258-1276, Dec. 2013.
[https://doi.org/10.1016/j.robot.2013.09.004]

-
K. R. Guruprasad and T. D. Ranjitha, "CPC Algorithm: Exact Area Coverage by a Mobile Robot Using Approximate Cellular Decomposition", Robotica, Vol. 39, No. 7, pp. 1141-1162, Oct. 2020.
[https://doi.org/10.1017/S026357472000096X]

-
C. S. Tan, R. Mohd-Mokhtar, and M. R. Arshad, "A Comprehensive Review of Coverage Path Planning in Robotics Using Classical and Heuristic Algorithms", IEEE Access, Vol. 9, pp. 119310-119342, Aug. 2021.
[https://doi.org/10.1109/ACCESS.2021.3108177]

-
S. Lloyd, "Least squares quantization in PCM", IEEE Transactions on Information Teory, Vol. 28, No. 2, pp. 129-137, Mar. 1982.
[https://doi.org/10.1109/TIT.1982.1056489]

-
F. Aurenhammer, "Voronoi diagrams—a survey of a fundamental geometric data structure", ACM Computing Surveys, Vol. 23, No. 3, pp. 345-405, Sep. 1991.
[https://doi.org/10.1145/116873.116880]

-
D. Puig, M. A. Garcia, and L. Wu, "A new global optimization strategy for coordinated multi-robot exploration: Development and comparative evaluation", Robotics and Autonomous Systems, Vol. 59, No. 9, pp. 635-653, Sep. 2011.
[https://doi.org/10.1016/j.robot.2011.05.004]

- H. Bast and S. Hert, "The Area Partitioning Problem", in Proceedings of the 12th Canadian Conference on Computational Geometry Fredericton, New Brunswick, Canada, Aug. 2000.
-
A. Rubinstein, "Perfect Equilibrium in a Bargaining Model", The Econometric Society, Vol. 50, No. 1, pp. 97-109, Jan. 1982.
[https://doi.org/10.2307/1912531]

-
A. C. Kapoutsis, S. A. Chatzichristofs, and E. B. Kosmatopoulos, "DARP: Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning", Journal of Intelligent & Robotic Systems, Vol. 86, pp. 663-680, Jan. 2017.
[https://doi.org/10.1007/s10846-016-0461-x]

-
P. Fazli, A. Davoodi, and A. K. Mackworth, "Multi-Robot Repeated Area Coverage: Performance Optimization Under Various Visual Ranges", 2012 Ninth Conference on Computer and Robot Vision, Toronto, ON, Canada, pp. 298-305, May 2012.
[https://doi.org/10.1109/CRV.2012.46]

-
P. Fazli, A. Davoodi, and A. K. Mackworth, "Multi-robot repeated area coverage", Autonomous Robots, Vol. 34, No. 4, pp. 251-276, Mar. 2013.
[https://doi.org/10.1007/s10514-012-9319-7]

-
J. O’Rourke, "Art Gallery Theorems and Algorithms", Oxford University Press, Vol. 31, No. 2, Jun. 1987.
[https://doi.org/10.1137/1031076]

-
S. C. Pereira, E. J. S. Pires, and P. B. M. Oliveira, "Ant-Balanced Multiple Traveling Salesmen: ACO-BmTSP", Algorithms 2023, Vol. 16, No. 1, pp. 1-17, Jan. 2023.
[https://doi.org/10.3390/a16010037]

-
I. Kara and T. Bektas, "Integer linear programming formulations of multiple salesman problems and its variations", European Journal of Operational Research, Vol. 174, No. 3, pp. 1449-1458, Nov. 2006.
[https://doi.org/10.1016/j.ejor.2005.03.008]

- A. Rexhepi, A. Maxhuni, and A. Dika, "Analysis of the impact of parameters values on the Genetic Algorithm for TSP", International Journal of Computer Science, Vol. 10, No. 3, pp. 158-164, Jan. 2013.

2023년 2월 : 금오공과대학교 전자공학부(공학사)
2023년 3월 ~ 현재 : 금오공과대학교 전자공학부 석사과정
관심분야 : 다중 로봇 커버리지, 다중 로봇 리스케줄링

2015년 8월 : 서울대학교 전기컴퓨터학부(공학박사)
2015년 9월 ~ 2018년 2월 : 삼성전자 생산기술연구소 책임연구원
2018년 3월 ~ 현재 : 금오공과대학교 전자공학부 제어 및 로봇전공 부교수
관심분야 : 다중로봇 SLAM, 다중 로봇 커버리지