협업 신호 추출을 통한 그래프 추천 시스템상의 지속 학습
초록
그래프 신경망 기반 추천 시스템을 위한 지속 학습 연구들은 그래프 구조와 정보 보존을 위한 다양한 방법을 제시하였다. 하지만 추천 시스템의 그래프 구조에서 핵심 요소로 사용되는 협업 신호를 반영한 연구는 존재하지 않는다. 본 논문에서는 그래프 신경망 기반 추천 시스템에서 협업 신호를 효과적으로 활용하는 새로운 지속 학습 방법을 제안한다. 사용자별 시점에 따른 그래프 구조를 협업 신호의 형태로 저장하고 새로운 데이터에서 추출된 협업 신호를 통해 갱신하는 접근법을 제안한다. 이를 통해 과거의 정보를 보존하면서도 새로운 정보를 효율적으로 반영하는 지속 학습이 가능하다. 최종적으로 실험을 통해 제안하는 방법이 기존 그래프 신경망 기반 추천 시스템의 지속 학습 방법들보다 성능이 우수함을 증명하였다.
Abstract
Previous recommender systems based on graph neural network have proposed various methods for preserving graph structure and information. However, no studies have considered collaborative signals, which are a key element in the graph structure of recommender systems. In response, we propose a novel continual learning method that effectively utilizes collaborative signals in the recommender systems based on graph neural network. By storing and updating user-specific temporal graph structures in the form of collaborative signals, this approach can efficiently incorporate new information while preserving past knowledge. Finally, our experiments demonstrate that this method outperforms existing continual learning methods for recommender systems.
Keywords:
distributed graph database, recommender systems, collaborative filtering, cloud computingⅠ. 서 론
최근 추천 시스템 연구는 대부분 그래프 신경망을 기반으로 한다[1]. 그래프 신경망은 노드 간 연결 정보를 메시지 패싱의 형태로 이용한다. 이는 연결된 이웃의 정보를 효과적으로 반영하고, 협업 신호(Collaborative signal)를 포착하여 노드의 표현력을 강화함으로써 추천 시스템의 성능을 향상시켰다[2]. 그러나 노드의 증가와 노드 사이의 연결 관계의 추가는 모든 데이터를 사용하는 기존의 그래프 신경망에서 자원 소모의 증가시키는 원인이 되었다. 이에 따라, 그래프 신경망 기반 추천 시스템에서도 새로운 데이터만으로 학습을 수행하기 위해 지속 학습을 적용하는 연구가 증가하고 있다[3]-[5].
그래프 신경망 기반 추천 시스템에서는 다른 분야의 지속 학습 연구와 마찬가지로 Memory Replay 방법[3]과 Regularization 방법[5]-[7]을 주로 사용한다. Memory Replay는 과거 데이터의 일부를 샘플링하여 그래프상의 노드 간 연결 관계를 보존할 수 있지만, 데이터가 늘어감에 따라 필요한 샘플링의 크기가 커진다[4]. Regularization은 추가적인 손실함수를 도입하여 과거의 정보를 효과적으로 보존하지만, 새로운 정보를 반영하는데 한계가 있다[8].
Memory Replay와 Regularization은 지속 학습의 성능이 보장되지만, 그래프 신경망 기반 추천 시스템에서 가장 중요한 요소인 협업 신호를 반영하지 못한다. 이는 그래프상 노드의 연결 관계에 내재된 정보를 충분히 활용하지 못함을 의미한다. 하지만 그래프 기반 지속 학습에서는 제한된 데이터의 사용으로, (1) 학습이 지속되면서 그래프의 구조가 변화하거나[9] (2) 노드의 영향력이 변화하는 문제가 발생한다[10]. 따라서, 그래프 기반 지속 학습에서 협업 신호를 모델링하는 것은 어려운 문제이다.
본 논문에서는 그래프 신경망 기반 추천 시스템의 지속 학습에서 협업 신호를 활용하는 방안을 제시한다. 우선, 사용자별 협업 신호를 행렬의 형태로 저장하여 과거 데이터의 구조와 이웃에게서 받는 영향력을 보존한다. 이후, 새로운 데이터의 정보를 담고 있는 협업 신호를 추출하여 사용자의 협업 신호를 갱신한다. 최종적으로 갱신된 협업 신호와 사용자의 임베딩 변화를 반영하여 추천을 진행한다. 이를 통해 새로운 데이터만 사용하여, 과거의 협업 신호와 새로운 협업 신호를 모두 반영하는 것이 가능하다.
본 논문은 2장에서 본 연구와 관련된 그래프 신경망 지속 학습과 관련된 선행 연구를 설명한다. 3장에서는 본 연구에서 가장 중요한 협업 신호와 관련된 예비 지식을 기술한다. 4장에서 본 논문에서 제시하는 협업 신호 기반 지속 학습을 그래프 신경망 기반 추천 시스템에 적용하는 방법을 제시한다. 5장에서는 다양한 실험을 통하여 제안 방법의 유의미함을 증명한다. 마지막으로 6장에서는 논문을 정리하고 향후 연구 방향을 제시한다.
Ⅱ. 관련 연구
2.1 그래프 신경망 기반 지속 학습
그래프 신경망은 그래프 데이터를 입력으로 사용하는 신경망으로, 그래프의 구조 정보를 메시지 패싱(Message passing)을 통해 학습한다[11]. 그래프 구조는 시간에 따라 지속해서 확장되는 특징이 있어[12], 지속 학습의 필요성이 대두되었다. 그래프 신경망 기반 지속 학습 연구는 크게 Memory Replay[9][12][13], Regularization[14], 그리고 이외의 방법[15]으로 구분된다.
추천 시스템 연구에서도 사용자와 상품이 연결된 그래프 구조를 주로 활용한다[8]. 하지만 이분 그래프라는 특성과 데이터 희소성 문제, 그리고 이웃 노드로부터 받는 영향 크다는 특징 때문에, 컴퓨터 비전이나 자연어처리 분야의 그래프 기반 지속 학습과는 다른 방식이 요구된다[6].
2.2 Memory Replay 방식
Memory Replay 방식은 이전 학습 단계에서 사용된 데이터 중 일부를 샘플링하여 그래프의 구조 정보를 보존한다[16].
ER-GNN[9]은 상황별 노드를 선택하는 전략 두 가지와 파라미터 변화도를 사용해 영향력이 큰 노드를 선택하는 전략을 제안한다.
제안한 전략들을 기반으로 다음 학습 단계에서 다시 사용할 데이터를 선택한다. SGNN-GR[13]은 랜덤워크에 기반한 생성 모델을 사용해, 과거의 정보와 비슷한 가상의 노드와 이웃 관계를 생성한다. 이를 통해 과거의 정보에 대한 접근 없이 기존 정보를 보존하여 망각 문제를 해결하였다.
추천에서는 기존의 데이터와 새로 들어온 데이터의 차이에 의해 사용자의 취향이 변화하며, 이는 추천의 결과에 영향을 미친다[17]. 따라서 추천 시스템에서의 Memory Replay 방식은 기존 데이터와 새로 들어온 데이터 사이의 유사성을 측정하여 사용자의 취향이 유지되는 방식을 주로 사용한다.
IncreGNN[12]은 새로운 데이터가 그래프에 추가되었을 때, 새로 들어온 데이터에 영향을 받은 노드와 그렇지 않은 노드를 중요도에 따라 샘플링한다. 이후 과적합을 방지하기 위해 이전 모델의 파라미터 중요도에 따른 Regularization을 수행한다.
하지만 샘플링으로 구조를 보존하면 데이터가 늘어날 때마다 보존해야 하는 데이터의 양이 증가하는 문제점이 있다[10]. 본 논문에서는 추출된 협업 신호를 사용하여 샘플링 없이 그래프의 구조 정보를 다음 단계의 학습에 전달하는 방식을 사용한다.
2.3 Regularization 방식
Regularization은 새로운 학습이 기존 학습 모델에서 크게 벗어나지 않도록 하는 방법이며, 주로 손실함수를 사용하여 기존 정보를 보존한다[18].
Continual GNN[10]은 새로운 데이터가 기존의 노드에 영향을 주어 생기는 패턴을 포착하고, 기존의 데이터 샘플링과 더불어, 손실함수를 사용한 Regularization을 통해 기존 패턴을 보존한다. TWP[14]는 Weight Regularization 기법으로, 그래프 어텐션 신경망을 활용하여 파라미터마다 손실함수의 gradient magnitude를 중요도의 척도로 사용해 중요한 파라미터를 보존한다.
추천 시스템에서 Regularization 방법은 그래프의 구조 정보를 노드와 노드 사이의 관계 형태로 보존하는 방식을 통해 기존의 정보를 보존한다.
GraphSAIL[6]은 그래프의 구조 정보를 local과 global로 나누어 새로운 데이터와 비교하고, self-embedding distillation을 통해 기존의 정보를 보존한다. LWC-KD[7]는 모델에서 각 레이어를 통과한 히든 임베딩을 이용해 knowledge distillation을 수행함으로써 모델이 학습한 정보를 보존한다. PIW[11]는 LWC-KD를 발전시킨 모델로 사용자의 과거 데이터와 현재 데이터 사이의 차이를 계산하여 각 사용자의 취향이 과거의 학습 데이터와 차이가 얼마나 다른지를 평가한다. 평가 결과를 바탕으로 기존 데이터의 정보를 얼마나 보존할지 결정한다.
하지만 이러한 방식들은 기존의 정보를 유지하려는 성향이 강하기 때문에 빠르게 변화하는 데이터 세트에 대응하지 못하는 단점이 있다[19]. 또한, 여러 손실함수를 사용해 기존의 정보를 보존하는 학습 방법을 사용하여 학습이 직관적으로 이루어지지 못하며 단점이 있다[20]. 이를 보완하기 위해 본 논문에서는 새로운 데이터 학습으로 얻어진 협업 신호를 사용해 기존 협업 신호를 갱신하는 방식으로 이 문제를 극복하였다.
2.4 이외의 방식
Memory replay와 Regularization 방식 이외에도 다양한 방법들이 그래프 지속 학습에서 연구되었다.
FGN[15]은 각 노드의 이웃 관계 정보를 담은 독립된 특징 그래프(Feature graph)를 사용해 지속 학습을 수행한다. 이후 특징 그래프를 사용한 신경망을 통해 노드의 임베딩을 업데이트한다. 이를 통해 각 노드를 독립적으로 사용해 그래프 구조 정보가 반영된 임베딩을 구한다. 하지만 여전히 과거의 정보가 반영된 특징 그래프를 만들기 위해 과거 데이터 샘플링이 필요하다.
DEGC[4]는 Model Isolation이라는 새로운 방법을 제시하였다. 이는 기존 모델에서 일부 중요한 파라미터만 남기고 제거한 다음, 새로운 데이터를 바탕으로 학습한 모델의 파라미터를 혼합하는 방식이다. 이를 통해 장기 선호와 단기 선호를 분리하여 반영할 수 있지만, 학습 가능한 파라미터가 반드시 필요하다. 따라서 학습 가능한 파라미터를 최소화하여 협업 신호를 사용하거나 그래프 구조의 이점을 활용하는 방식에는 적용이 불가능하다.
이러한 단점을 극복하기 위해 본 논문에서는 과거 데이터 샘플링 없이도 이웃 관계를 나타내는 협업 신호를 추출하여 기존 정보를 보존한다. 또한, 학습 파라미터를 추가할 필요 없이 사용자의 협업 신호로 추출된 이웃 관계를 통해 사용자의 취향을 고려할 수 있다.
Ⅲ. 방법론
본 논문에서 제안하는 방법은 추천 시스템상의 그래프 기반 지속 학습에서 협업 신호를 추출하고 갱신하는 것이 가능하다. 이를 통해 사용자의 기존 이웃 관계를 보존하고, 새로운 이웃 관계를 반영한 지속 학습이 가능하다.
3.1 전체구조
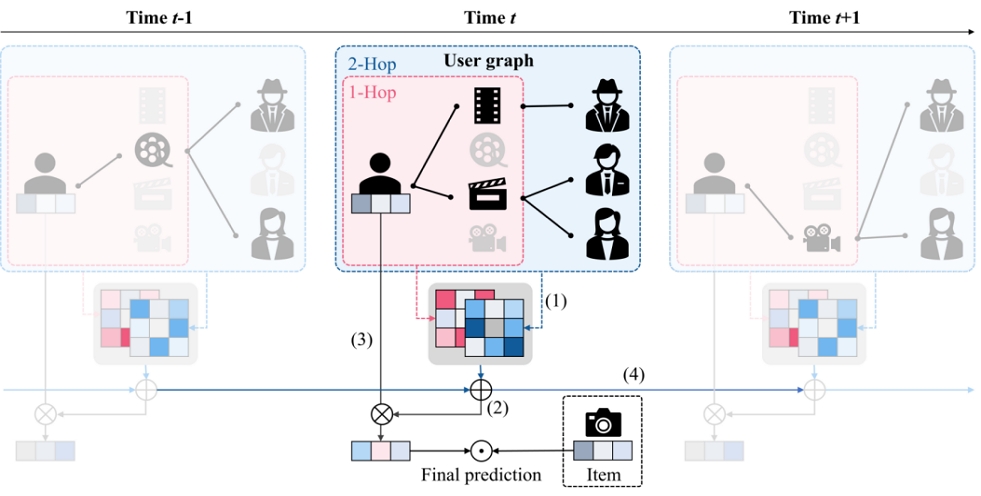
전체구조에 대한 개요는 그림 1과 같다. 먼저 그림 1의 (1)은 기존의 지속 학습이 아닌 그래프 신경망을 사용한 학습을 통해 이웃 정보가 반영된 사용자 임베딩을 구하는 과정이다. 이 과정을 바탕으로 현재 시점(time t)의 데이터에 존재하는 협업 신호를 추출한다. 이렇게 추출된 협업 신호는 (2)에서 과거 시점(time t-1)의 협업 신호와 합쳐 과거와 현재 시점을 반영하도록 갱신한다. 최종적으로 나온 협업 신호는 (3)에서 추천을 위한 현재 시점의 임베딩 계산에 사용되며, (4)에서 다음 시점(time t+1)에 전달되어 현재까지의 정보를 보존하는 용도로 사용된다.
3.2 협업 신호
이 장에서는 본 논문에서 사용하는 협업 신호에 대해 알아본다. 협업 신호란 사용자-상품 상호작용 안에 잠재된 정보이다. 이를 활용하면 고차원 이웃 관계(High-order neighbor relationship)를 사용해 노드의 표현력을 강화하여 추천의 성능을 높일 수 있다[2]. 협업 신호는 사용자의 과거 행동 데이터를 사용해 학습되며, 이 과정에서 이웃과의 관계 정보가 반영된다.
지속 학습에서는 시간에 따라 그래프의 연결 관계가 변화한다[21]. 따라서 시점마다 각 노드와 연결된 이웃의 수와 노드 간 경로가 변화하게 된다. 이는 시점에 따라 노드가 영향을 받는 협업 신호가 변화함을 의미한다.
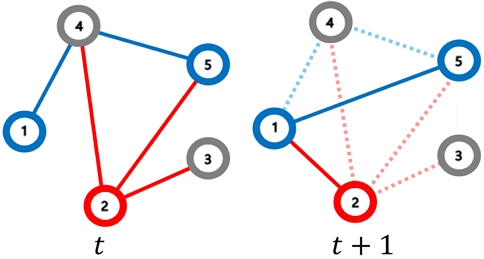
그림 2는 시점에 따라 데이터가 바뀔 때 나타날 수 있는 관계 정보 변화에 대한 그림이다. 그림 2의 파란색 노드인 노드 1과 5는 t 시점에서 2-hop 관계에 있지만, t+1 시점에서는 1-hop으로 변화한다. 이 두 노드 사이의 경로 변화는 협업 신호의 차이를 유발한다[22].
또한, 이웃 개수의 변화로 이웃 노드에 끼치는 영향력도 변화한다[2]. 빨간색 노드 2의 경우, t 시점에서는 3개의 1-hop 이웃이 있었으나, t+1 시점에서 그래프의 연결 구조가 바뀌는 것을 볼 수 있다. 이에 따라 노드 2가 이웃 노드에 끼치는 영향력이 변화한다. 이러한 영향력의 변화는 그래프 신경망을 통해 노드가 반영하는 이웃 정보에 차이를 유발한다. 이러한 정보의 변화를 본 논문에서는 협업 신호 자체로 보존하는 방식으로 대응한다.
3.3 협업 신호 추출
우선, 협업 신호를 추출하려면 사용자의 이웃 관계를 반영한 임베딩을 구해야 한다. 이를 위해 본 논문에서는 LightGCN[23]과 같은 그래프 신경망 추천 모델을 사용하였다. 그래프 신경망을 사용한 추천 모델의 레이어는 식 (1)과 같다.
| (1) |
위 식 (1)에서 은 레이어 l을 통과했을 때의 은닉 상태(Hidden state)를 의미하며, L은 전체 레이어의 개수를, 는 초기 임베딩을 의미한다. 여기서 Aggregation 함수는 메시지 패싱을 통해 초기 임베딩을 이웃의 관계가 반영된 임베딩으로 변환시키는 함수이며, 기반이 되는 그래프 신경망 추천 모델에 따라 달라진다. 여기서 l번째 레이어를 통과해서 나온 은닉 상태 에는 l-hop 이웃과의 관계가 반영되어 있다. 따라서 L개의 레이어를 사용한 그래프 신경망을 통과해서 나온 최종 임베딩 은 L-hop까지의 이웃 관계가 반영된다.
사용자의 임베딩과 최종 임베딩 사이의 협업 신호를 명시적으로 추출하기 위해, 본 논문에서는 Kabsh-umeyama 알고리즘[24]을 사용하였다. 이 기법은 동일한 선형 공간 내에서 서로 다른 위치의 두 벡터의 변환 정보를 근사하는 방법이다. t 시점에서 레이어 l의 Aggregation 함수를 근사하는 행렬을 라고 한다면, 식 (1)을 근사한 식 (2)는 다음과 같다.
| (2) |
은 식 (3)을 최대한 만족시키는 결과로 추정할 수 있다.
| (3) |
식 (3)에서 ∥∥F는 프로비니어스 노름(Frobenius Norm)을 의미한다.
식 (3)을 만족하는 는 그래프 신경망으로 포착된 현재 시점의 이웃 관계를 나타내는 협업 신호이다.
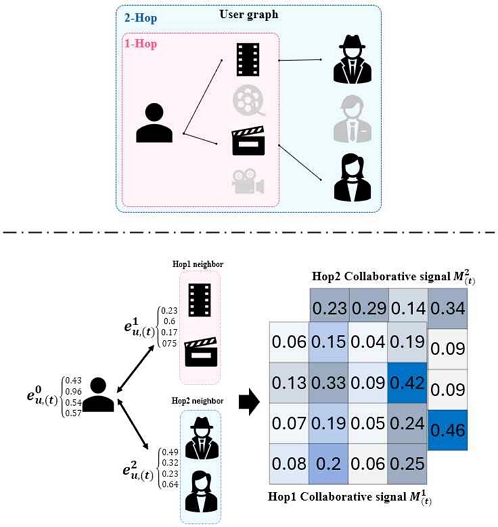
그림 3은 협업 신호를 추출하는 과정을 나타낸다. (1)의 사용자 그래프는 그래프 신경망을 통과하며 이웃의 임베딩이 반영된 은닉 상태를 계산한다. 이후, (2)에서 사용자의 초기 임베딩과 각 hop 이웃의 정보가 반영된 은닉 상태의 관계인 협업 신호 은 위 식 (2)와 (3)을 통해서 추출된다.
마지막으로 최종 임베딩에서만 협업 신호를 추출할 경우, 모든 hop의 정보가 혼합되어 있는 상태에서 협업 신호를 추출하게 된다. 이를 분리하여 각각의 hop별 협업 신호를 추출할 경우 모든 hop의 정보가 합쳐져 있는 상태에서 추출할 때보다 근사의 오차를 줄였다.
3.4 협업 신호 갱신
본 논문에서는 t 시점에서 l-hop 이웃의 정보가 반영된 사용자의 임베딩 (), t 시점에서 추출된 사용자의 협업 신호 (), t-1 시점까지의 사용자의 협업 신호 ()를 사용, 이전 시점의 협업 신호에 현재 시점의 협업 신호를 반영해 갱신한다.
이를 위해 기존의 협업 신호를 이전 시점의 임베딩과 현재 시점의 임베딩 간 발생하는 차이만큼 조정해 주어야 한다. 협업 신호는 두 임베딩 사이의 변환 관계를 나타낸다는 점에서 선형변환으로 볼 수 있다. 따라서 임베딩의 변화가 발생할 경우, 기존 행렬이 가리키는 공간도 변하게 된다. 이를 방지하기 위해 기존의 협업 신호를 임베딩의 변화만큼 보정한다. 보정된 협업 신호 는 식 (4)와 같다.
| (4) |
는 이전 시점까지 누적된 협업 신호를 의미하고, D(t)는 새로운 데이터를 이용한 학습으로 초기 임베딩이 변화한 정도를 나타내는 행렬이다.
최종 협업 신호는 보정된 기존의 협업 신호()와 현재 시점의 협업 신호 ()를 혼합해서 구할 수 있다. 이는 식 (5)를 통해 계산된다.
| (5) |
이때 α는 기존 협업 신호와 현재 협업 신호의 반영 비율을 정하는 하이퍼파라미터로, α가 클수록 기존 정보를 더 많이 반영하며, 작을수록 현재 정보를 더 많이 반영한다.
3.5 예측 평점 추론
최종적으로 추천 결과 도출을 위한 예측 평점 추론은 다음과 같은 과정을 거친다. 먼저, 최종적으로 계산된 협업 신호 ()를 사용하여 사용자의 임베딩에 협업 신호를 주입한다. 최종 사용자 임베딩()은 식 (6)을 통해 계산된다.
| (6) |
각 hop별 협업 신호를 반영한 사용자 임베딩()을 계산하여, 이를 hop별 중요도를 반영한 가중치 al와 곱한다. 최종 사용자 임베딩은 이들의 가중합으로 구해지며, 본 논문에서는 각 hop별 가중치를 동일하게 설정하였다.
최종적으로 사용자 u의 상품 i에 대한 예측 평점 rui는 식 (7)과 같이 정의되며, 이때 상품의 임베딩은 기반 모델을 통해 얻은 결과이다.
| (7) |
Ⅳ. 실 험
본 논문에서는 추천 시스템의 지속 학습에서 협업 신호를 고려하는 제안 방식이 얼마나 효과적인지 검증하기 위해 다양한 실험을 진행하였다.
4.1 실험 환경
본 논문에서는 추천 시스템의 평가에서 많이 쓰이는 MovieLens(ML-1M)[25]와 Taobao2014[26] 데이터셋을 사용해 제안하는 방법론의 성능을 검증하였다. 데이터에 대한 자세한 특성은 표 1과 같다.
실제 추천이 이루어지는 환경과 비슷한 한 번에 들어오는 데이터의 양이 적고 희소한 상황을 만들고, 장기적인 관점에서 시점별 성능의 변화를 확인하기 위해 베이스 블록 1개와 별도의 학습 및 성능 평가를 위한 증가 블록을 10개의 시점으로 나누었다.
학습은 다음과 같이 이루어진다. 베이스 블록은 일반 모델을 사용해 학습을 수행한다. 이때 본 논문은 LightGCN[23]을 사용하였다. 증가 블록의 데이터부터는 각각의 지속 학습 방법에 맞추어 새로운 데이터만을 사용해 학습을 수행하였다. 학습된 모델은 다음 시점의 데이터 중 50%를 사용해 Validation을 수행하였고, 이를 통해 찾은 최적의 모델을 나머지 50%의 데이터를 사용하여 Test를 수행하고, 해당 결과를 사용하였다. 본 실험에서는 모든 모델에서 새로운 상품이나 사용자의 경우 기존에 등장한 임베딩들의 평균을 초기값으로 사용하였다. 또한 새로 등장한 사용자의 경우 해당 시점에서 학습된 협업 신호를 전부 반영하였다. 최종적으로 추천 결과 상위 20개를 사용하여 Recall과 NDCG를 계산하여 평가 지표로 사용하였다.
본 모델 및 아래 실험에 사용되는 LightGCN의 학습값은 다른 논문에서 주로 사용되는 값인 레이어 수 은 3, 학습률 0.001, 그리고 배치 크기 2048을 사용하였다. 최대 에포크는 500으로 설정하였으며 다른 논문에서 실험한 대로 Validation 값이 2회 이상 감소하지 않을 시 조기 종료하였다[6]. 본 모델에서 필요한 값은 실험을 통해 Taobao2014에서는 0.2로, ML 1M에서는 0.6으로 적용하였다.
4.2 Base model
Finetune : 가장 Naive한 방식의 지속 학습 방법론으로, 기존 모델의 파라미터를 새로 들어온 데이터에 전달하여 학습을 수행하는 방식이다.
Full-Batch : 모든 데이터를 사용해서 모델을 다시 학습하는 방식이다. 학습의 성능이 좋아질 수도 있지만, 모든 데이터를 학습에 사용하여 자원 소모가 매우 많은 방식이다.
GraphSAIL[6] : 그래프 신경망 기반 추천 시스템에 지속 학습을 최초로 적용한 모델이다. 그래프 구조 정보의 차이와 노드 임베딩의 차이를 이용한 손실함수로 과거의 정보를 보존한다.
LWC-KD[7] : 각 레이어를 통과해 나온 임베딩을 기반으로 Contrastive Knowledge Distillation을 수행하여 모델이 학습한 정보를 보존한다.
PIW[5] : 기존의 정보를 얼마나 보존하며, 새로운 정보는 얼마나 반영할지를 정하는 가중치가 사용자마다 다른 방식이다. LWC-KD를 Knowledge Distillation 방법으로 사용한다.
4.3 실험 결과 분석
실험은 다음 질문을 기반으로 설계하였다.
RQ1. 기존 방법론보다 제안하는 방법이 성능적으로 우수한가?
RQ2. α값은 모델의 성능에 어떠한 영향을 끼치는가?
RQ1. 기존 방법론보다 제안하는 방법이 성능적으로 우수한가?
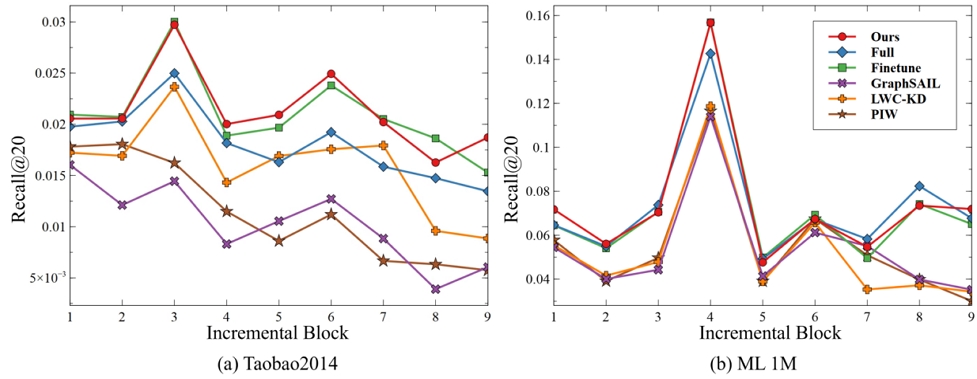
먼저 제안하는 방법과 기존 그래프 기반 추천 지속 학습 방법론의 성능을 비교하였다. 표 2와 그림 4를 통해 실험 결과를 확인할 수 있으며, 전반적으로 본 논문에서 제안하는 방법이 기존의 지속 학습 방식보다 높은 성능을 유지하고 있음을 알 수 있다.
제안하는 방법이 다른 Baseline 모델들보다 성능이 좋은 이유는 그래프 구조를 파악하는 방식의 차이 때문이다. Baseline 모델들은 그래프 구조를 파악하기 위해 클러스터링 및 노드의 이웃 임베딩과의 차이 평균 등을 사용한다. 이러한 방식은 실제 새로 들어오는 데이터의 양이 매우 적은 추천 시스템 환경에 효과적이지 못하다[27]. 추가적으로 이러한 문제는 Regularization 및 Knowledge Distillation에서 과안정성(Over-Stability)을 유발할 수 있다.
반면 본 논문이 제안하는 모델은 기존의 데이터와 새로운 데이터의 그래프 구조를 협업 신호의 형태로 직접 추출하여 이용한다. 따라서 적은 데이터를 사용해도 자세한 그래프 구조를 파악할 수 있으며, α값을 통해 새로운 데이터의 반영 비율을 조절할 수 있어 안정적인 성능을 보여준다.
Taobao2014 데이터셋은 표 1에 의하면 사용자의 수보다 상품의 수가 많으며 데이터가 희소하다. 이는 사용자의 선택 폭이 넓어 많은 취향의 변화를 데이터셋에 포함됨을 의미한다. 이에 따라 사용자의 단기적인 선호, 즉 현재 시점의 데이터가 중요해진다. 이러한 내용은 Finetune 방식이 Full-Batch 방식보다 우수한 성능을 보임에서 확인 할 수 있다. 또한 Baseline 모델에서 LWC-KD 방식이 높은 성능을 기록했는데, 이는 GraphSAIL과 같이 복잡한 계산보다 레이어를 통해 반영된 이웃 관계를 파악하는 것이 성능에 긍정적인 영향을 미쳤기 때문이다. 본 연구는 레이어를 통해 반영된 이웃 관계를 협업 신호의 형태로 추출할 뿐만 아니라 기존 협업 신호와 새로운 협업 신호를 조합하여 새로운 데이터를 충분히 반영하였다. 이를 통해 LWC-KD보다 높은 성능을 기록하였다.
표 1에서 ML-1M 데이터셋은 사용자보다 아이템의 개수가 적고, 데이터의 밀도가 더 높다. 이에 따라 사용자는 적은 선택의 폭을 가지고 있으며, 장기적인 선호가 많은 영향을 성능에 많은 영향을 끼친다. 이는 Full-Batch 방식이 Finetune 방식보다 더 높은 성능을 보이는 것에서 확인 할 수 있다. 추가로, Baseline 모델 중 PIW가 성능이 높은 것을 확인 할 수 있는데, 이는 홉 별 이웃 관계뿐만 아니라 사용자의 취향 변화에 대한 정보를 함께 고려할 때 효과적임을 의미한다. 본 논문의 제안 방법은 이웃 관계 정보를 담고 있는 협업 신호를 시점에 따라 점진적으로 혼합하여 사용자의 과거와 현재 시점 사이의 취향 변화를 균형 있게 모델링함으로써, 다른 Baseline 연구들보다 높은 성능을 보였다.
RQ2. α값은 모델의 성능에 어떠한 영향을 끼치는가?
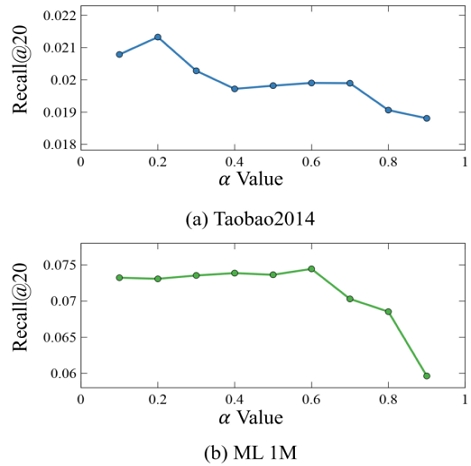
그림 5는 α값에 따른 Recall의 평균값을 그래프로 나타낸 것이다. 이를 통해 데이터셋의 특성과 α값의 관계를 확인 할 수 있다. 먼저 두 데이터셋 모두 α값이 0.8 이상이 되면 급격하게 성능이 감소하는 것을 확인할 수 있다.
이는 과안정성 현상이 발생한 것으로 기존의 데이터가 과하게 반영되어 새로운 정보를 충분히 반영하지 못해서 발생하는 문제이다.
Taobao2014 데이터셋에서는 작은 α값을 설정하여 새로운 정보를 많이 반영할수록 성능이 높아짐을 확인할 수 있다. 이는 단기 취향이 큰 영향을 끼치는 데이터셋의 특성에 따른 것이다. 반면 ML-1M의 경우 0.1부터 0.5까지 완만하다가 0.6에서 정점을 달성하는 것을 확인 할 수 있다. 이는 새로 들어오는 데이터들이 기존 사용자의 데이터와 비슷한 특징을 가지고 있기 때문이다. 위의 결과를 통해 데이터 특성에 따른 다양한 α값의 적용으로, 데이터마다 최적의 성능을 구할 수 있음을 확인할 수 있다.
Ⅴ. 결 론
본 논문에서는 협업 신호를 활용하여 그래프 기반 추천 시스템의 지속 학습 성능을 높이는 방법을 제안하였다. 이 방법은 사용자의 이웃에 대한 정보를 협업 신호의 형태로 추출하여, 기존 정보의 보존이 가능하다. 또한, 새로운 데이터에서 추출한 협업 신호를 사용해 기존 사용자의 협업 신호를 갱신한다. 이를 통해 사용자의 과거 정보와 현재 정보를 모두 반영한 협업 신호를 사용하여 지속 학습을 수행한다. 실험을 통해 협업 신호를 사용할 경우 추천 시스템의 지속 학습 성능이 높아짐을 확인하였다.
향후 연구로는 사용자 개개인의 취향 변화를 협업 신호에 적용하는 방법을 제시하고자 한다. 또한, 본 논문에서는 초기 임베딩과 은닉 상태 사이의 관계를 선형 근사를 통해 추출하고 있는데, 그래프 신경망의 비선형적인 특성을 반영하여 협업 신호를 추출하는 방법을 제시하고자 한다.
Acknowledgments
본 연구는 2024년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원(NRF-2022R1C1C1012408, 우수신진연구)과 정보통신기획평가원의 지원(No.2022-0-00448/RS-2022-II220448, 인간처럼 회상이 가능한 인공 신경망 지속학습 플랫폼 개발, No.RS-2022-00155915, 인공지능융합혁신인재양성(인하대학교))을 받아 수행된 연구임
References
-
C. Gao, et al., "A Survey of Graph Neural Networks for Recommender Systems: Challenges, Methods, and Directions", ACM Transactions on Recommender Systems, Vol. 1, No. 1, pp. 1-51, Mar. 2023.
[https://doi.org/10.1145/3568022]

-
X. Wang, X. He, M. Wang, F. Feng, and T. Chua, "Neural Graph Collaborative Filtering", In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR '19), Paris France, pp. 165-174, Jul. 2019.
[https://doi.org/10.1145/3331184.3331267]

-
D. Wei, Y. Gu, Y. Song, Z. Song, F. Li, and G. Yu, "IncreGNN: Incremental Graph Neural Network Learning, in by Considering Node and Parameter Importance", Database Systems for Advanced Applications.(DASFAA '22), Vol. 13245, pp. 739-746, Apr. 2022.
[https://doi.org/10.1007/978-3-031-00123-9_59]

-
B. He, X. He, Y. Zhang, R. Tang, and C. Ma, "Dynamically Expandable Graph Convolution for Streaming Recommendation", In Proceedings of the ACM Web Conference 2023 (WWW '23), Austin TX USA, pp. 1457-1467, Apr. 2023.
[https://doi.org/10.1145/3543507.3583237]

-
Y. Wang, Y. Zhang, A. Valkanas, R. Tang, C. Ma, J. Hao, and M. Coates, "Structure Aware Incremental Learning with Personalized Imitation Weights for Recommender Systems", In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI '23), Washington, DC, USA, Vol. 37, No. 4, pp. 4711-4719, Feb. 2023.
[https://doi.org/10.1609/aaai.v37i4.25595]

-
Y. Xu, Y. Zhang, W. Guo, H. Guo, R. Tang, and M. Coates, "GraphSAIL: Graph Structure Aware Incremental Learning for Recommender Systems", In Proceedings of the 29th ACM International Conference on Information & Knowledge Management (CIKM '20), pp. 2861-2868, Oct. 2020.
[https://doi.org/10.1145/3340531.3412754]

-
Y. Wang, Y. Zhang, and M. Coates, "Graph Structure Aware Contrastive Knowledge Distillation for Incremental Learning in Recommender Systems", In Proceedings of the 30th ACM International Conference on Information & Knowledge Management (CIKM '21), pp. 3518-3522, Nov. 2021.
[https://doi.org/10.1145/3459637.3482117]

- D. Brignac, N. Lobo, and A. Mahalanobis, "Improving Replay Sample Selection and Storage for Less Forgetting in Continual Learning", In 2023 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW '23), pp. 3532-3541, Oct. 2023.
-
F. Zhou and C. Cao, "Overcoming Catastrophic Forgetting in Graph Neural Networks with Experience Replay", In Proceedings of the Thirty-fifth AAAI Conference on Artificial Intelligence (AAAI '21), Vol 35, No. 5, pp. 4714-4722, Feb. 2021.
[https://doi.org/10.1609/aaai.v35i5.16602]

-
J. Wang, G. Song, Y. Wu, and L. Wang, "Streaming Graph Neural Networks via Continual Learning", In Proceedings of the 29th ACM International Conference on Information & Knowledge Management (CIKM '20), pp. 1515-1524, Oct. 2020.
[https://doi.org/10.1145/3340531.3411963]

-
F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini, "The Graph Neural Network Model", IEEE Transactions on Neural Networks, Vol. 20, No. 1, pp. 61-80, Jan. 2009.
[https://doi.org/10.1109/TNN.2008.2005605]

-
X. Zhang, D. Song, and D Tao, "Continual Learning on Graphs: Challenges, Solutions, and Opportunities", arXiv preprint, Feb. 2024.
[https://doi.org/10.48550/arXiv.2402.11565]

-
J. Wang, W. Zhu, G. Song, and L. Wang, "Streaming Graph Neural Networks with Generative Replay", In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD '22), Washington DC USA, pp. 1878-1888, Aug. 2022.
[https://doi.org/10.1145/3534678.3539336]

-
H. Liu, Y. Yang, and X. Wang, "Overcoming Catastrophic Forgetting in Graph Neural Networks", In Proceedings of the Thirty-fifth AAAI Conference on Artificial Intelligence (AAAI '21), Vol. 35, No. 10, pp. 8653-8661, May 2021.
[https://doi.org/10.1609/aaai.v35i10.17049]

- C. Wang, Y. Qiu, D. Gao, and S. Scherer; "Liflong Graph Learning", In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR '22), New Orleans, LA, USA, pp. 13719-13728, Jun. 2022.
- D. Rolnick, A. Ahuja, J. Schwarz, T. Lillicrap, and G. Wayne, "Experience Replay for Continual Learning", In Proceedings of the 32th International Conference on Neural Information Processing Systems (NIPS '19), Vancouver, Canada, pp. 350-360, 2019.
-
G. I. Webb, R. Hyde, H. Cao, H. L. Nguyen, and F. Perirjean, "Characterizing concept drift", Data Mining and Knowledge Discovery, Vol. 30, pp. 964-994, Apr. 2016.
[https://doi.org/10.1007/s10618-015-0448-4]

- H. Ahn, S. Cha, D. Lee, and T. Moon, "Uncertainty-based Continual Learning with Adaptive Regularization", Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, No. 395, pp. 4392-4402, Dec. 2019.
- O. Ostapenko, P. Rodriguez, M. Caccia, and L. Charlin, "Continual learning via local module composition", In Proceedings of the 35th International Conference on Neural Information Processing Systems (NIPS '21), NY, United States, pp. 30298-30312, Dec. 2021.
- R. Groenendijk, S. Karaoglu, T. Gevers, and T. Mensink, "Multi-Loss Weighting With Coefficient of Variations", In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV '21), pp. 1469-1478, 2021.
-
W. Yu, W. Cheng, C. C. Aggarwal, K. Zhang, H. Chen, and W. Wang, "NetWalk: A Flexible Deep Embedding Approach for Anomaly Detection in Dynamic Networks", In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining(KDD '18), London, United Kingdom, pp. 2672-2681, Jul. 2018.
[https://doi.org/10.1145/3219819.3220024]

-
Y. Wang, Y. Zhao, Y. Zhang, and T. Derr, "Collaboration-Aware Graph Convolutional Network for Recommender Systems", In Proceedings of the ACM Web Conference 2023 (WWW '23), Austin TX USA, pp. 91-101, Apr. 2023.
[https://doi.org/10.1145/3543507.3583229]

-
X. He, K. Deng, X. Wang, Y. Li, Y. Zhang, and M. Wang, "LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation", In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR '20), pp. 639-648, Jul. 2020.
[https://doi.org/10.1145/3397271.340106]

-
J. Lawrence, J. Bernal, and C. J. Witzgall, "A Purely Algebraic Justification of the Kabsch-Umeyama Algorithm", In Journal of Research of the National Institute of Standards and Technology, Vol. 124, pp. 1-6, Oct. 2019.
[https://doi.org/124.10.6028/jres.124.028]

- Movie lens 1M dataset, https://grouplens.org/datasets/movielens/1m, [accessed: Sep. 23, 2024]
- Taobao2014 dataset, https://tianchi.aliyun.com/dataset/46, [accessed: Sep. 23, 2024]
-
S. Ahmadian, N. Joorabloo, M. Jalili, and M. Ahmadian, "Alleviating data sparsity problem in time-aware recommender systems using a reliable rating profile enrichment approach", Expert Systems with Applications, Vol. 187, pp. 115849, Jan. 2022.
[https://doi.org/10.1016/j.eswa.2021.115849]


2023년 : 인하대학교 컴퓨터공학과(공학사)
2023년 ~ 현재 : 인하대학교 전기컴퓨터공학과 석사과정
관심분야 : 그래프 신경망, 추천 시스템, 지속 학습

2017년: 고려대학교 컴퓨터공학과(공학석사)
2017년 ~ 현재 : SK 홀딩스 인공지능 엔지니어
2023년 ~ 현재 : 인하대학교 전기컴퓨터공학과 박사과정
관심분야 : 딥러닝, 컴퓨터비전, 추천 시스템

2012년 : 고려대학교 컴퓨터통신공학부(공학사)
2018년 : 고려대학교 컴퓨터학과(공학박사)
2018년 : 고려대학교 컴퓨터정보통신연구소 연구교수
2019년 ~ 2020년 : 세종대학교 데이터사이언스학과 조교수
2020년 ~ 현재 : 인하대학교 컴퓨터공학과 조교수
관심분야 : 데이터 마이닝, 추천 시스템, 지속 학습, 그래프 신경망