차원축소를 이용한 수치 데이터 비식별화 기법
초록
최근 빅데이터 분석기술이 많은 주목을 받고 있다. 빅데이터 취급 과정에서 개인 신원이 노출될 경우 사회적 문제 및 물질적 피해로 이어질 수 있으며, 이러한 문제를 방지하기 위해 데이터로부터 개인식별을 할 수 없게 하는 비식별화 기술이 존재한다. 그러나 기존의 비식별화 기술은 개인식별 방지에만 초점을 맞추고 있으며 집단 특성 분석은 방지할 수 없다. 본 논문에서는 기존 비식별화의 한계점을 분석하고, 특히 집단 특성 분석에 따른 문제점을 지적한다. 그리고 이러한 문제점을 극복하기 위한 새로운 차원축소 기반의 비식별화 기법을 제안한다. 제안한 방식은 인가된 자에 한해서만 비식별화 데이터를 추출할 수 있으며, 인가되지 않은 자는 차원축소된 데이터로부터 비식별화된 데이터를 추출할 수 없으므로 집단 특성 분석을 차단할 수 있다. 또한 데이터 추론 공격, 재식별 공격으로부터 안전하므로 클라우드 환경을 통해 안전하게 데이터를 공유할 수 있다.
Abstract
Recently, big data analysis technology has garnered significant attention. When personal identities are exposed during the handling of big data, it can lead to social issues. However, existing de-identification methods focus solely on preventing individual identification and cannot prevent the analysis of group characteristics. This paper analyzes the limitations of existing de-identification methods, particularly pointing out issues related to group characteristic analysis. It proposes a new de-identification technique based on dimensionality reduction to overcome these problems. The proposed method can only extract de-identified data for authorized individuals, and unauthorized individuals cannot extract de-identified data, which can block group characteristic analysis. Additionally, it is safe from data inference attacks and re-identification attacks, allowing for secure data sharing through cloud environments.
Keywords:
de-identification, privacy protection, PCA, dimensionality reduction, big data securityⅠ. 서 론
빅데이터 분석 기술은 미래 경쟁력을 좌우하는 중요한 기술이다. 최근 빅데이터 시대로 진입하면서 빅데이터 분석의 중요성은 모두가 공감하고 있다. 그러나 이러한 빅데이터 분석에는 다양한 부작용이 존재할 수 있다. 특히 개인정보에 대한 보안적 조치가 허술한 경우, 해당 개인은 프라이버시에 대한 침해를 받게 되며 정보가 노출됨에 따른 다양한 형태의 피해를 받을 수 있다. 이러한 문제를 방지하기 위한 데이터 비식별화 기술이 존재한다. 비식별화는 데이터의 주체인 개인을 식별할 수 없도록 만드는 기법으로, 이러한 비식별화를 달성하기 위해 가명화, 총계처리, 데이터 마스킹, 차분 프라이버시와 같은 다양한 방법이 사용되어 오고 있다[1][2]. 그러나 기존의 비식별화 방법에는 한계점이 존재한다. 특히 기존의 방식에서는 원본 데이터와의 대조를 통하여 재식별 가능성 위험이 공통적으로 존재하며, 비록 정보 주체인 개인이 식별되지 않더라도 개인이 속한 집단이 식별되는 경우 데이터 집단의 특성 분석을 통하여 개인에 대한 민감한 정보가 추정되는 경우가 있을 수 있다.
본 논문에서는 이러한 문제를 지적하고 새로운 비식별화 기법을 제안한다. 제안한 방법에서는 PCA(Principal Component Analysis) 기반의 차원축소 및 복원을 통하여 정보 손실이 최소화된 비식별화된 데이터를 추출한다. 제안한 방식에서는 데이터 공유시 차원 축소된 데이터만 공유하므로 개인 식별이나 데이터 집단의 특성 분석을 위한 추론공격, 재식별 공격에서 안전함을 보인다. 또한, 고유값 및 고유벡터를 인가된 그룹에 한하여 공유하며, 이러한 고유값과 고유벡터가 없이는 비식별화된 데이터 자체를 추출할 수 없어 안전하다.
본 논문의 구성은 다음과 같다. 2장은 비식별화 방식에 대한 한계점과 관련 연구동향을 언급하였으며, 3장에서는 비식별화 방식의 주요 논점과 본 논문에서 새롭게 제안하는 비식별화 방식에 대해 기술한다. 4장에서는 제안한 비식별화 방식에 대한 실험 결과를 나타내고 이를 기반으로 제안한 방식의 안전성과 효율성에 대하여 논한다. 마지막으로 5장에서는 결론 및 향후 연구방향에 대하여 기술한다.
Ⅱ. 관련 연구
2.1 기존 비식별화 기법 및 한계점
데이터 비식별화 기법이란 구체적으로 개인을 식별할 수 있는 정보를 제거하거나 변환하는 작업을 수행하여 개인의 프라이버시를 보호할 수 있는 기법이다[3]. 이러한 데이터 비식별화 기법은 주로 빅데이터의 분석에 앞선 전처리 작업으로 수행되는 경우가 많으며, 만일 데이터상에 민감정보가 포함되어 있더라도 그 데이터의 주체가 누구인지를 식별하지 못하게 함으로써 데이터 주체의 프라이버시를 보호할 수 있다[4].
일반적으로 이러한 비식별화를 위해 가명화, 총계처리, 데이터 마스킹, 차분 프라이버시와 같은 방법이 사용된다. 가명화란 개인 식별자를 다른 식별자로 대체하는 방법이다. 그러나 원본 데이터를 보유하고 있는 자는 개인을 재식별화할 수 있는 위험이 존재한다. 총계처리는 개별 데이터 항목을 범위 데이터로 묶는 방식이다. 이러한 총계처리 방식은 데이터 집합이 작거나 특성을 가지고 있는 경우에 재식별될 수 있는 위험이 존재한다. 또한 데이터 마스킹은 민감한 데이터를 변환하거나 가리는 방법이며, 이러한 마스킹 기법은 데이터 분석 과정에서 효율성을 저하시킬 수 있으며, 효용성 향상을 위해 적은 범위에 대해 마스킹을 수행할 경우 데이터 재식별화의 가능성이 높아진다는 단점이 있다.
차분 프라이버시 방식은 데이터에 대하여 랜덤한 노이즈를 추가하여 원본 데이터를 보호하는 방법이다. 만약 안전성을 위하여 데이터의 랜덤성을 높이는 경우 데이터 분석 결과의 효용성을 크게 저하시킬 수 있으며, 반대로 효용성을 위한 작은 범위의 랜덤성을 적용할 경우 재식별화 가능성이 존재한다.
2.2 비식별화 관련 연구
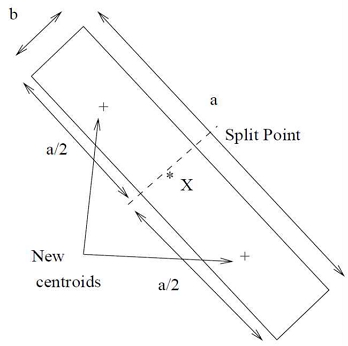
C. C. Aggarwal et al.[5]은 Condensation 알고리즘을 이용한 프라이버시 보호 데이터 마이닝 기법을 제안하였다.
해당 연구에서는 원본 데이터를 익명화된 데이터 세트로 매핑하여 여러 차원 간의 상관관계를 유지할 수 있는 방법을 제안하였다. 이러한 방식은 수행 과정에서 별도의 알고리즘이 필요하지 않다는 점에서 효율적이며, 데이터의 평균과 상관관계 정보를 유지할 수 있다는 장점이 있다. 그러나 예외적인 일부 데이터가 있을 경우는 효과적으로 반영되기 어려우며 새로운 데이터 추가 시 기존 그룹에 대하여 분할 및 재구성에 대한 절차가 필요하다는 번거로움과 이에 대한 오버헤드가 존재한다는 단점이 있다. 그림 1은 Aggarwal et al.이 제안한 방식을 나타내며 데이터 그룹을 분할하여 새로운 통계 그룹을 생성하는 과정을 시각적으로 설명하고 있다. 이러한 방식은 프라이버시를 유지하면서도 데이터의 통계적 특징을 보존한다는 장점이 있다.
T. S. Gal et al.[6]은 통계 분석을 위한 데이터 유용성을 유지가 가능한 의학 데이터 비식별화 방법을 제안하였다. 제안한 방법은 Aggarwal et al.이 제안한 Condensation 알고리즘을 개선하여 k-mean 클러스터링 기법을 사용하여 데이터의 통계적 특성을 일정부분 보존하도록 설계하였다. 제안한 방법은 통계적 속성을 유지하면서도 개별 데이터의 식별을 어렵게 한다는 장점은 있으나, 비식별화를 위한 k-mean 클러스터링의 수행 과정에서의 오버헤드가 존재할 수 있다. 또한 클러스터 내의 데이터 수가 현저히 적은 경우 클러스터 내의 데이터가 공격자에게 쉽게 재식별될 수 있다는 단점 또한 존재한다.
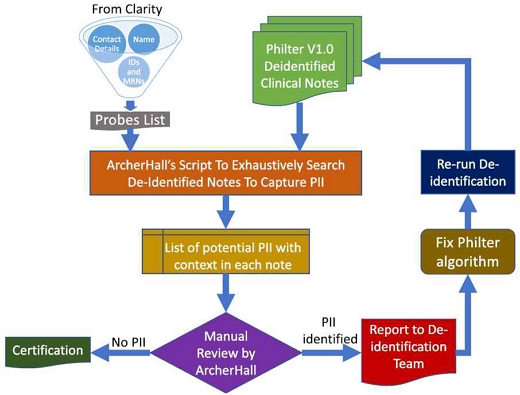
L. Radhakrishnan et al.[7]은 임상 텍스트 데이터를 비식별화하여 연구자들이 프라이버시가 보호된 데이터를 사용할 수 있도록 하는 시스템을 제안하였다. 제안 방식에서 MongoDB와 멀티스레딩을 통하여 성능 향상이 가능하도록 하였고, 여러 단계의 인증을 통하여 HIPAA 규정을 준수하는 Philter V1.0 기반의 비식별화 기법을 제안하였다. 그러나 제안한 방식은 통합적인 비식별화 시스템 자체로써 의미가 있으며, 실제 세부적인 비식별화 방법에 대한 정확성 및 효용성, 보안성 문제를 극복 가능한 구체적인 알고리즘을 연구 내용에서 포함하고 있지는 않다. 그림 2는 Radhakrishnan et al.이 제안한 인증 프로세스를 시각적으로 설명한다. 이러한 절차를 통해 PII(개인 식별 정보)를 탐지하여 필터 알고리즘의 성능을 향상시킬수 있으며, 최종적으로 HIPAA 기준에 부합하는 비식별화를 수행할 수 있다.
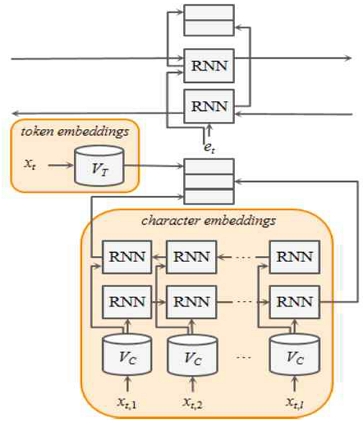
K. Lee et al.[8]은 NeuroNER을 기반으로 한 문맥 강화 비식별화 시스템(CEDI)를 제안하였다. 비정형 데이터에서 비식별화 시스템을 적용하고자 하는 경우, 각 문장단위로 독립적으로 처리하여 문장 경계를 넘어선 의존성을 판단하는 것에는 한계가 있다. 그림 3에서는 K. Lee et al.이 제안한 방식을 그림으로 나타낸다. 여기에서 각 토큰은 문자 임베딩과 토큰 임베딩이 결합되어 다시 biLSTM 레이어에 전달하는 방식으로 복합적인 특징을 학습할 수 있다. 이러한 과정을 통해 문장 내 토큰 간의 관계를 효과적으로 학습하여 비식별화를 수행할 수 있다.
해당 논문에서 제안한 방식은 Deep Affix Features와 Attention Mechanism을 활용하여 이러한 의존성 문제를 해결하고자 하였다. 그러나 해당 논문에서 제안한 방식은 원본 데이터가 비정형 데이터인 경우에만 효과적이며 일반적으로 분석되는 정형 개인정보 데이터에 대해서는 효과적으로 적용할 수 없다는 단점이 있다.
2.3 PCA를 이용한 차원축소
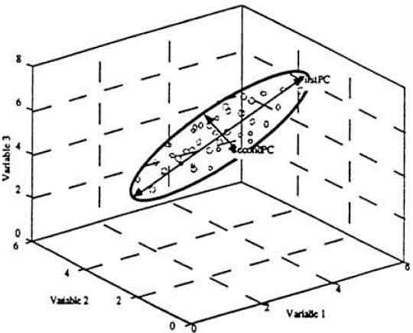
PCA는 데이터에 가장 가까운 초평면(Hyperplane)을 구한 다음, 데이터를 이 초평면에 투영(Projection)하여 차원을 줄이는 통계적 기법이다. 이러한 PCA 기반 차원 축소를 이용하면 데이터의 주요 정보와 패턴을 유지하면서 영향도가 낮은 차원을 제거하여 본 데이터의 성향에서 크게 벗어나지 않는 차원이 축소된 데이터를 추출할 수 있다[9][10].
그림 4는 PCA의 개념을 시각적으로 나타낸다. 3차원 데이터 세트에서 첫 번째 주성분은 데이터의 최대 분산을 설명하고, 두 번째 주성분은 첫 번째 주성분과 직교하는 방향으로 그 다음으로 큰 변동을 설명한다. 이러한 PCA를 통해 데이터의 차원을 축소하면서도 중요한 정보는 유지할 수 있다.
PCA 기반의 차원 축소를 통하여 데이터 분석에 어려움을 초래하는 차원의 저주를 피할 수 있으며, 데이터의 변동성이 높은 주성분을 선택하므로 중요한 정보를 유지하고 불필요한 노이즈를 자연스럽게 제거할 수 있다는 장점이 있다. 또한, PCA 기반으로 차원이 축소된 데이터는 원래의 차원으로 복원이 가능하다. 그러나 차원 축소 과정에서 비가역적인 정보 손실이 발생되어 원본 그대로 복원이 되는 것이 아닌 근사치를 갖는 값으로 복원된다. 본 논문에서는 이러한 특성을 비식별화 데이터 변환에 적용하는 방안을 제안한다.
Ⅲ. 제안 방식
3.1 비식별화의 주요 논점과 개선방안
비식별화 방식은 정보주체의 보호가 핵심이며, 데이터 분석을 통한 집단의 특성 분석 행위에 대해서는 보호할 수 없다. 본 논문에서는 이러한 문제를 지적하고, 이에 대한 개선방안을 제안하고자 한다.
가명화, 총계처리, 데이터 마스킹, 차분 프라이버시 등의 기존의 비식별화 방식은 구조적으로 비식별화를 완료하더라도 데이터 집단의 특성을 일부 노출하고 있는 문제를 가지고 있다.
기존의 비식별화 방식은 정보 주체가 누구인지에 대한 분석을 방지하는 것이 주요한 관점이며, 데이터 집단 자체의 특성은 그대로 노출하고 있다.
예를 들어 가명화의 경우, 데이터 개수 분석을 방지하기 위해 k-익명성을 적용하였다고 하더라도 적어도 1/k의 데이터에 대해서는 유의미한 정보를 가지고 있게 된다. 총계처리의 경우는 데이터에 대한 대략적인 윤곽을 나타내고 있으며, 정밀하게 데이터를 식별할 수는 없어도 정보의 대략적인 윤곽은 파악할 수 있게 된다. 데이터 마스킹의 경우는 일부를 마스킹 처리 하더라도 마스킹하지 않은 부분에 대해서는 평문이 노출되게 된다. 보안성을 높이기 위하여 최대한 많은 부분에 대하여 마스킹 처리를 할 경우, 데이터의 효용성이 크게 저하되어 일반적인 수준의 데이터 분석이 어려울 수 있다.
차분 프라이버시를 통하여 노이즈를 적용하는 방식으로 원본 데이터를 보호하고자 하는 경우에도 마찬가지로 원본 데이터의 정보 주체를 파악하기 어렵게 하는 것이 주요 관점이지만, 데이터상에 데이터의 윤곽은 그대로 나타나므로 데이터 집단의 특성은 그대로 노출하고 있다고 볼 수 있다.
데이터 집단의 특성을 노출하는 것은 구조적으로 기존 비식별화 방식의 취약점이다. 경우에 따라, 정보 주체 뿐만 아니라 집단의 특성까지 노출하고 싶지 않은 경우도 있다는 것을 고려해야 한다. 여기서는 몇 가지 사례를 들어 집단 특성 노출에 따른 문제점을 지적하고자 한다.
① 정치적 민감성이 있는 경우
특정 지역의 정치적 성향이나 사회적 이슈에 대한 데이터가 있을 때, 해당 데이터의 공개로 인하여 불필요한 논쟁이나 갈등을 초래할 수 있다. 특히 민감한 사회적 문제를 다루는 경우 이에 대한 빅데이터를 공개하는 것은 문제의 소지가 있다.
② 사생활 침해 우려가 있는 경우
비식별화된 데이터라 하더라도 집단 특성의 노출을 통하여 그 집단에 속한 개인의 민감성을 침해할 가능성이 존재한다. 예를 들어 특정 지역 또는 특정 직업군에 따른 범죄율과 같은 집단 특성이 파악되는 경우, 해당 집단에 속한 개인의 경우 민감하게 반응할 우려가 있다.
③ 기업 측면에서의 데이터 보호
기업의 고객 데이터를 비식별화하여 공개할 경우, 구매 패턴이나 선호도와 같은 고객의 특성 파악을 통해 기업의 주력 분야 및 경쟁 우위 분야 등이 경쟁사에 의해 파악될 수 있다. 경쟁사는 이러한 데이터를 해당 기업보다 우위를 차지하기 위한 다양한 전략을 세우는데 활용할 수 있다.
비식별화된 데이터는 다양한 경로에 의해 공유될 수 있다. 특히, 비식별화된 데이터가 오픈 API 형태로 제공되거나, 클라우드 서버에 그대로 노출될 수도 있다. 구조적으로 비식별화된 데이터는 복원을 통한 특정 정보 주체인 개인의 식별은 어렵다는 가정을 할 수 있으나, 데이터 집단의 분석은 가능할 수 있어 그에 대한 적절한 조치가 필요하다.
따라서 비식별화된 데이터라 하더라도 인가된 자에 한하여 공유가 되는 것이 바람직하다. 비록 인가되지 못한자가 데이터를 수집하더라도, 수집된 데이터를 분석하는 것은 어렵게 하는 조치가 필요하다.
일반적으로 이러한 상황을 방지하기 위하여 비식별화된 데이터에 대하여 암호화를 하는 경우를 생각해볼 수 있다. 그러나 암호화의 경우는 암호키 관리의 번거로움이 있으며 비식별화와 암호화 이중 적용에 따른 오버헤드가 존재할 수 있다. 또한, 빅데이터 중 일부 선별된 데이터만 분석하고자 하는 경우에도 전체 데이터에 대한 복호화를 수행해야 할 수 있다. 따라서 이러한 문제를 해결하는데 암호화를 적용하는 것은 적절하지 않다고 볼 수 있다.
3.2 차원축소 기반 데이터 비식별화 모델 설계
본 논문에서 제안하는 비식별화의 새로운 방안으로 PCA를 이용한 차원축소를 통하여 데이터를 비식별화하는 방식을 제안한다.
제안하는 차원축소 기반의 비식별화는 원본 데이터에 노이즈를 추가하는 차등 프라이버시 방식과는 접근이 다르다고 할 수 있다. 제안하는 방식은 PCA를 통하여 고차원 데이터를 저차원으로 축소하면서 일부 정보가 비가역적으로 손실되므로, PCA를 통하여 차원 축소된 데이터를 원본 데이터로 완벽히 되돌리는 것은 사실상 불가능하다. 이러한 PCA 기반 차원축소를 통하여 원본 데이터에 비가역적인 변형을 가져오는 것으로, 차원 축소된 데이터는 자연스럽게 개인식별이 가능한 정보는 제거된다. 또한, 데이터의 주요 패턴이나 분포를 유지한 상태에서의 비식별화가 가능하다는 장점이 있다.
PCA 기반의 차원축소 과정에서 데이터의 정보 손실이 발생하며, 따라서 데이터 분석의 유용성 확보를 위하여 과도한 차원축소를 적용하지 않는 것이 바람직하다.
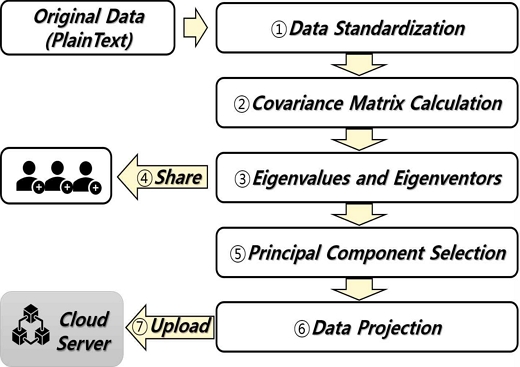
본 논문에서 제안하는 차원축소 기반의 데이터 보호 모델은 그림 5와 같다.
최초 평문데이터는 개인의 민감정보가 포함되어 있는 데이터이며, 본인 식별이 어렵도록 데이터에 대한 적절한 비식별화가 필요하다. 그러나 데이터 비식별화 방식을 적용하였더라도 데이터 분석을 통한 재식별화의 위험성이 존재하고 있어 비식별화된 데이터를 안전하게 공유하는 구조가 필요하다.
본 논문에는 다음과 같이 차원축소 방식을 이용하여 차원 축소된 데이터만을 공유하도록 한다.
① 데이터 표준화 : 변수 간 스케일 차이로 주성분이 특정 변수에 지나치게 치우쳐 왜곡되는 것을 방지하기 위하여 표준화를 수행한다.
② 공분산 행렬 계산 : 변수들 간의 관계를 나타내기 위해 두 변수 간의 상관관계를 측정하는 값인 공분산 행렬을 계산한다.
③ 고유벡터 및 고유값 계산 : 공분산 행렬에서의 고유벡터와 고유값을 계산한다. 고유벡터는 데이터의 주 방향을 나타내며, 고유값은 그 방향의 중요도를 나타낸다.
④ 고유벡터와 고유값 공유 : 고유벡터와 고유값은 인가된 사람들에게만 공유한다. 이러한 고유벡터와 고유값은 비밀 정보로 취급하여야 하며, 인가된 자만 접근할 수 있는 보안 채널을 통해 안전하게 전달되어야 한다.
⑤ 주성분 선택 : 고유벡터 정렬 후 데이터의 주요 특성을 설명하는 상위 고유값에 해당하는 고유벡터를 선택하여 새로운 축을 정의한다.
⑥ 데이터 투영 : 선택된 주성분을 이용하여 데이터를 저차원 공간으로 투영하여 차원을 축소한 새로운 값을 얻는다.
⑦ 데이터 저장 및 공유 : 차원이 축소된 데이터는 클라우드 서버, 공공데이터, 오픈 API등으로 공개될 수 있다. 그러나 해당 데이터를 수집하더라도 고유벡터 및 고유값을 알지 못하면 유의미한 데이터를 분석할 수 없다.
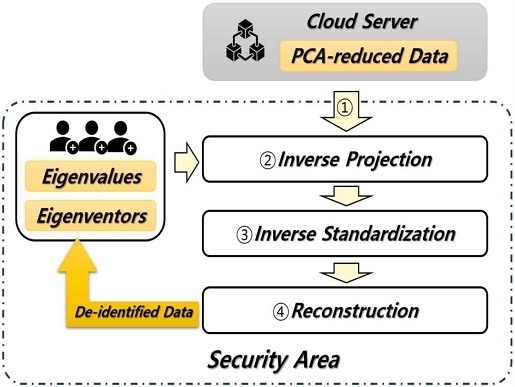
차원축소된 데이터는 그 자체로서 비식별화 데이터가 은닉된 상태이며 차원축소된 상태에서는 유의미한 데이터 분석을 수행할 수 없다. 고유값과 고유벡터를 가진 자에 한하여 원래 차원으로 복원하여 비식별화된 데이터를 추출할 수 있다. 비식별화 데이터의 추출 모델은 그림 6과 같다.
① 데이터 수집 : 차원 축소된 데이터를 클라우드 서버, 공공데이터, 오픈 API 등의 경로를 통하여 수집한다.
② 역투영 : 차원 축소된 데이터를 선택된 고유벡터를 사용하여 원본 데이터의 차원으로 역투영하여 데이터를 확장한다.
③ 역표준화 : 원본 데이터의 평균을 추가하여 데이터를 되돌리는 작업을 수행한다.
④ 복원을 통한 비식별화 데이터 추출 : 원본과 동일한 차원의 복원된 데이터를 얻을 수 있으며, 데이터는 원본과 동일하지 않은 근사치 데이터를 얻는다. 이러한 데이터는 비식별화된 데이터로 간주하며, 해당 데이터에 대한 유의미한 분석을 실행할 수 있다. 이러한 비식별화 데이터는 인가된 자에 한하여 생성할 수 있다.
3.3 세부 절차
① 데이터 표준화 단계
n개의 샘플과 p개의 특성을 갖는 원본 데이터 행렬 X에 대하여 식 (1)과 같이 표준화된 데이터 행렬 Z를 구한다. 여기에서 μ는 각 변수의 평균 벡터이며, σ는 각 변수의 표준편차 벡터이다.
| (1) |
② 고유값 및 고유벡터 추출 단계
표준화된 데이터 행렬 Z에 대하여 공분산 행렬 C를 식 (2)와 같이 계산한다. 여기에서 n은 샘플의 수를 의미한다.
| (2) |
이후 다음과 같이 공분산 행렬 C의 고유값 λi와 고유벡터 vi를 식 (3)과 같이 계산한다. 여기에서, 고유벡터 vi는 주성분을 나타낸다.
| (3) |
여기에서 고유값 λi와 고유벡터 vi는 인가된 자에 한해서만 공유하는 값이다. 고유값 λi와 고유벡터 vi를 알지 못하면 축소된 데이터를 복원한 비식별화 데이터를 생성할 수 없다.
③ 차원 축소된 데이터의 추출단계
이후 고유값이 큰 순서대로 k개의 주성분을 선택하여, 축소된 차원 데이터 Y를 식 (4)와 같이 계산한다. 여기에서 Vk는 선택된 k개의 고유벡터로 구성된 행렬이다.
| (4) |
이렇게 차원이 축소된 데이터 Y에 대한 고유값과 고유벡터를 알지 못할 경우 평문 데이터를 복원하는 것은 매우 어렵다. 이러한 차원이 축소된 데이터를 클라우드 서버, 공공데이터, 오픈API 등으로 안전하게 게시할 수 있다.
④ 데이터 공유 단계
비식별화 데이터에 대한 생성 권한을 가진 정당한 사용자에 대해서 고유값 λi와 고유벡터 vi를 공유한다. 만약 고유값 λi와 고유벡터 vi를 알고 있지못한 경우는 축소된 데이터를 복원할 수 없으며, 따라서 비식별화 데이터 또한 생성할 수 없다.
이후 축소된 차원 데이터 Y를 클라우드 서버, 공공데이터 등으로 자유롭게 게시하여 공개한다.
축소된 차원데이터는 그 자체로써 비식별화 데이터의 역할을 할 수 없으며, 원본데이터의 집단 특성을 노출하고 있지 않다. 원본 데이터에 대한 의미있는 데이터 분석을 수행하려면 이 축소된 차원 데이터 Y를 비식별화된 데이터로 변환해야 하며, 이는 인가된 자만 알고 있는 고유값 λi와 고유벡터 vi에 의해서만 비식별화 데이터로 복원이 가능하다. 여기에서 데이터의 복원은 평문 데이터 그대로 복원하는 것을 의미하는 것이 아니며, 평문데이터와 유사한 비식별화된 데이터로 복원되는 것을 의미한다.
① 데이터 수집 단계
비식별화 데이터 생성을 위하여 두가지 데이터가 필요하다. 먼저 차원축소된 데이터 Y와 인가된 자에게만 공유되는 고유값 λi 및 고유벡터 vi 값이다.
차원축소된 데이터 Y는 앞서 언급한 바와 같이 클라우드 서버, 오픈API, 공공데이터 개방과 같은 다양한 채널을 통하여 일반에 공개할 수 있다. 다만 차원축소된 Y는 그 자체만으로 비식별화된 데이터로 볼 수 없으며, 비식별화된 데이터가 은닉된 상태의 데이터로 보는 것이 타당하다. 이러한 차원축소된 데이터만으로는 집단의 특성 분석과 같은 유의미한 분석을 수행할 수 없다.
② 비식별화 데이터 생성단계
고유값 λi와 고유벡터 vi를 알고 있는 인가된 자는 차원 축소된 데이터로부터 복원을 통하여 비식별화 데이터를 생성할 수 있다. 고유벡터 행렬의 전치인 VkT를 통하여 식 (5)와 같이 축소된 차원데이터 Y를 원래 차원으로 복원하여 ZR을 구한다.
| (5) |
③ 최종 비식별화 데이터 생성단계
표준화된 데이터의 역변환을 통하여 원본 데이터 스케일로 변환하는 것으로 최종 비식별화 데이터를 생성할 수 있다. 앞서 연산한 ZR에 대하여 식 (6)으로 최종 비식별화된 데이터 XR을 추출할 수 있다.
| (6) |
Ⅳ. 제안 방식 분석
4.1 실험 결과
개인의 민감한 정보 및 개인식별이 가능한 데이터는 다양한 형태로 존재할 수 있으나, 이해의 직관성을 위하여 테스트를 위한 평문 샘플 데이터로써 키, 몸무게, 나이 데이터를 민감정보로 가정하고 테스트 데이터를 생성하였다. 본 논문에서 제안한 방식을 적용하여 생성된 원본 데이터에 대하여 차원축소를 수행하고, 해당 데이터의 복원을 통한 비식별화 데이터를 추출하는 과정을 수행하였다. 실험을 위하여 Colab 환경에서 Python 언어가 사용되었다.
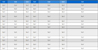
표 1에서 왼쪽의 데이터는 앞서 생성한 10건의 샘플 데이터를 나타내며, 오른쪽의 데이터는 차원축소 및 복원을 수행한 비식별화된 데이터를 나타낸다.
실험 결과 원본 데이터에 대하여 비식별화가 정상적으로 수행되었음을 알 수 있으며, 이렇게 추출된 비식별화 데이터를 원본 데이터로 되돌리는 것은 매우 어렵다. 또한, 차원축소와 복원을 통하여 데이터에 비가역적인 변형을 수행하였으나, 데이터 자체의 분포, 평균, 총계와 같은 특징은 그대로 가지고 있으므로 비식별화된 데이터로부터 유의미한 데이터 분석이 가능하다.
표 2에서는 표 1에 나타난 원본 데이터와 비식별화된 데이터에 대한 평균을 산출하였다. 표 2에서 나타난 것과 같이 비식별화된 데이터의 평균값도 원본의 평균값과 큰 차이 없이 유지하고 있으며, 비식별화된 데이터는 원본과 유사한 총합, 평균, 분포 등의 특성을 유지하고 있어 데이터 분석상의 효용성을 그대로 유지하고 있음을 확인할 수 있다.
고유값과 고유벡터를 소유하고 있는 자는 차원축소된 데이터로부터 차원 복원 작업을 수행하여 비식별화 데이터 추출이 가능하다. 표 1에서 나타난 비식별화 추출에 사용된 고유값과 고유벡터가 연산되는 과정은 다음과 같다. 먼저, 원본 데이터에 표준화를 수행한 결과인 데이터 행렬 Z는 아래와 같이 표현할 수 있다.
표준화된 행렬 Z는 전치행렬인 ZT와의 행렬 곱셈을 통하여 공분산 행렬인 C값을 계산할 수 있다.
이러한 공분산 행렬 C로부터 계산된 고유값과 고유벡터는 다음과 같다.
해당 결과에서 고유값은 데이터의 분산을 나타낸다. 즉, 고유값이 클수록 원래의 데이터를 가장 잘 설명한다고 볼수 있어 고유값의 크기를 기준으로 변환 차수만큼의 고유값과 고유벡터가 결정되었다. 해당 고유값과 고유벡터는 비밀 데이터로 간주되며, 인가된 그룹에 한하여 공유되어야 한다.
이후 원본 데이터 행렬에 고유벡터 행렬을 곱하여 새로운 저차원 공간으로 투영한다. 이 과정에서 원본 데이터는 주성분 축에 따라 재구성되며, 최종적으로 차원이 축소된 데이터를 얻을 수 있다.
표 3은 PCA로 차원 축소된 데이터를 나타낸다. 해당 데이터는 클라우드 서버, 공공데이터, 오픈 API등으로 공개될 수 있으며, 해당 차원 축소된 데이터만으로는 원본 데이터를 복원하기가 매우 어렵다. 또한 해당 데이터만으로 특정 개인의 추정뿐만 아니라 집단에 대한 특성 분석도 수행할 수 없어 안전하게 데이터를 공유할 수 있다.
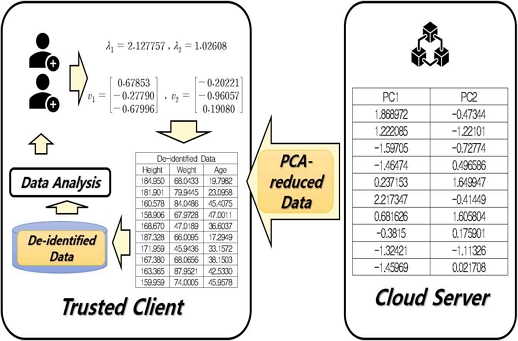
본 절의 실험에서 연산된 데이터는 그림 7과 같이 클라우드 영역과 신뢰된 클라이언트에 저장된다.
클라우드 서버에는 PCA로 차원 축소된 데이터가 저장되어 있으며, 해당 정보는 오픈 API 등으로 자유롭게 공유가 가능하다. 그리고 신뢰된 영역에서만 고유값과 고유벡터를 가지고 있으므로, 인가된 자에 한해서 차원축소된 데이터로부터 비식별화 데이터의 추출이 가능하다. 이러한 취급 방식을 통하여 비식별화 데이터 취급상의 안전성을 확보할 수 있다.
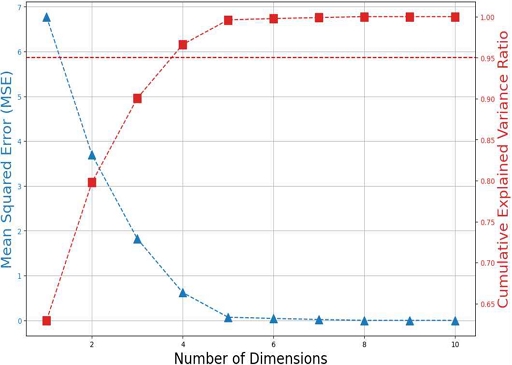
PCA 방식에서 최적의 차원 수를 결정하는 것은 데이터의 중요한 정보를 유지하는데 중요한 요소이다. 차원 축소 과정에서 비가역적인 정보의 손실이 나타나며, 데이터 분석의 효용성을 위하여 차원을 적절히 축소하여 대부분의 중요한 정보는 유지하도록 최적의 차원수를 결정하여 축소하여야 한다. 여기에서는 차원 수를 결정하기 위해 스크리 플롯(Scree plot)을 사용하여 설명된 분산 비율을 기준으로 최적의 차원을 결정하는 과정을 실험하였다.
설명된 분산비율은 주성분이 데이터의 분산을 얼마나 잘 유지하는지를 나타내며, 본 실험에서는 10개의 차원에 대해 설명된 분산비율이 95%가 되는 지점을 기준으로 차원 수를 결정하였다. 실험 결과 PC4가 되는 지점에서 95%의 분산을 보존하며, PC5부터는 차원을 늘리더라도 설명된 분산비율이 크게 변하지 않는 것을 확인할 수 있다. 따라서, 95%의 데이터를 보존하면서 축소할 수 있는 지점인 PC4만큼의 차원으로 축소하는 것이 적절함을 알 수 있다.
4.2 안전성 측면 분석
추론 공격을 통하여 데이터의 상관관계와 패턴을 분석하여 민감한 정보의 추정을 시도할 수 있다.
기존 총계처리, 가명화, 차분 프라이버시 방식의 경우 데이터의 상관관계와 패턴을 분석하여 원본 민감정보와 데이터 주체를 추론할 위험이 있다.
그러나 본 논문에서 제안한 방식은 데이터의 분산에 대한 설명이 가능한 주성분만을 남기고 나머지 정보를 제거한 차원이 축소된 데이터만을 공개한다. 본 논문에서 제안된 방식으로 공개되는 정보에서는 데이터 추론을 통한 개인 및 집단 민감정보 추정이 매우 어렵다. 원본 데이터의 특성을 가지고 있는 비식별화된 데이터는 고유값과 고유벡터를 알고 있는 인가된 자에 한해서만 추출이 가능하며, 공격자는 이러한 비식별화 데이터를 추출할 수 없다.
가명화는 개인 식별정보를 대체하는 방식으로 비식별화를 수행하며, 원본 데이터와의 연관성을 유지하고 있어 재식별의 가능성이 있다. 또한, 데이터 마스킹을 적용할 경우, 마스킹되지 않은 부분으로 인해 원본과 대조를 통한 재식별이 가능할 수 있다.
그러나 제안하는 방식에서 클라우드상에 공개되는 데이터는 차원이 축소된 데이터이므로 원본 대조를 통한 재식별 공격을 방지할 수 있다. 특히 고유값이 작은 주성분에 해당하는 데이터는 비가역적으로 삭제 및 축소를 수행하여 공격자가 데이터의 세부적인 특징을 파악하기 매우 어렵게 한다.
4.3 효율성 측면 분석
제안하는 방식은 원본 데이터의 중요한 특성을 유지한 상태에서 차원을 축소하고 복원 과정을 거치므로 원본 데이터의 정보 손실을 최소화한다. 차원축소 및 복원 과정에서 원본 데이터에 대한 비가역적인 손실이 발생하므로 비식별화된 데이터를 원본 데이터로 되돌리기는 매우 어렵다는 측면에서 보안성을 제공하면서, 또한 비식별화 수행 과정에서 최소한의 정보 손실만을 발생시키므로 데이터상의 통계적 질의나 집단의 특성 분석 등을 효율적으로 수행할 수 있다는 장점이 있다.
제안한 방식은 평문을 비식별화하면서 통계적 특징을 그대로 가지고 있으므로 총합, 평균 등 통계적 질의에서도 의미 있는 값을 가진다. 따라서 비식별화된 데이터에 대한 분석만으로도 데이터의 일반적인 특성이나 분포를 이해할 수 있다는 장점이 있으며 이러한 특성에 따라 데이터 분석, 머신러닝 모델링 등에 활용이 가능하다.
제안한 방식은 고유벡터와 고유값을 인가된 자에 한해서만 공유한다. 즉, 고유벡터와 고유값을 인지하지 못하는 경우 공개된 차원축소 데이터를 획득하더라도 정상적으로 비식별화 데이터를 생성할 수 없다. 이러한 측면은 비식별화 데이터에 대한 접근제어의 한가지 방안으로 활용할 수 있다.
또한 제안한 방식은 전체 데이터가 아닌 일부 데이터만을 획득하더라도 그에 대한 비식별화 데이터를 생성할 수 있다. 예컨대, 클라우드 서버상의 빅데이터가 방대할 경우, 특정 기준에 따른 일부 샘플만을 추출하여 비식별화를 수행하는 방식으로도 사용이 가능하다.
4.4 기존 방식과의 비교 논의
본 논문에서 제안한 방식은 비식별화 방식에 속한다. 일반적인 비식별화 방식은 구조적으로 평문에 대한 정보를 대략적으로 노출하고 있으나, 제안한 방식은 차원축소를 통하여 평문에 대한 정보를 노출하지 않고 안전하게 은닉할 수 있는 방안을 제공한다. 또한 차원축소된 데이터로부터 비식별화 데이터로 복원하기 위한 복원키(고유값, 고유벡터)를 제공한다는 점에서 암호화 방식과도 비교될 수 있다.
비식별화와 암호화는 서로 목적이 다르며, 비식별화의 목적은 데이터의 기밀성 확보가 아닌 개인 식별 방지가 주목적이다. 따라서 비식별화된 데이터의 경우 개인식별정보를 제외한 정보는 대부분 노출하게 된다. 다만 어떠한 방식으로 분석하더라도 개인을 식별할 수 없어야 한다는 관점이 중요하다.
그러나 암호화 방식의 경우 기밀성 제공이 주요 목적이 된다. 즉, 암호화 데이터는 어떠한 정보도 노출하지 않지만, 키를 통한 복호화를 수행하였을 경우에 개인식별정보를 포함한 평문이 그대로 복원된다. 키를 가진 자는 평문 복원이 가능하므로 암호화 방식은 비식별화의 목적으로는 사용할 수 없다.
만약 비식별화된 데이터에도 정보 노출을 방지하려면 비식별화 이후 암호화를 한번 더 수행을 해야 한다. 이러한 점은 비식별화, 암호화 알고리즘을 각각 별도로 수행한다는 점에서 오버헤드가 존재한다.
제안한 방식은 비식별화 방식이지만 그 자체로 데이터 은닉의 기능을 가지고 있어 별도로 암호화를 수행할 필요가 없다는 점에서 장점을 갖는다.
또한 제안한 방식은 키의 역할을 하는 고유값 및 고유벡터를 수집하여 복원을 수행하더라도 결과물로써 비식별화된 차원 축소된 데이터가 추출된다. 차원 축소 과정에서 비가역적인 정보 손실이 발생되므로 평문 그대로 복원이 되는 것이 아닌 근사치를 갖는 값으로 복원된다는 점에서 암호화 방식과는 차이가 있다. 즉, 본 논문에서 제안한 방식은 비식별화의 방안으로 사용되어야 하며, 암복호화의 목적으로는 사용할 수 없다.
제안한 방식은 기존의 비식별화 방식에서 보안성을 더한 방식이라는 부분에 의의가 있다. 기존의 비식별화 방식은 정보를 대략적으로 노출하지만 제안한 방식은 정보를 노출하지 않고 안전하게 공유가 가능하다는 장점이 있다.
Ⅴ. 결 론
빅데이터 분석 기술은 여러 산업에 이점을 가져올 수 있어 각광받는 기술이다. 그러나 이러한 빅데이터 분석 과정에서의 정보 노출 위험을 방지해야 하며, 특히 개인정보의 주체를 안전하게 보호하는 데이터 비식별화는 필수적이라고 할 수 있다.
지금까지 많은 비식별화 알고리즘이 제안되어 있으나, 원본 대조를 통한 재식별화의 위험과 집단 특성 분석에 따른 개인 프라이버시 침해에 대한 위험이 존재하였다. 따라서 본 논문에서는 이러한 문제를 극복하고 빅데이터를 안전하게 취급할 수 있는 새로운 데이터 비식별화 기술을 제안하였다.
제안한 방법은 PCA 기반 차원축소와 복원을 이용하여 비식별화된 데이터를 생성할 수 있으며, 비식별화된 상태에서 총합, 평균 등에서 의미있는 통계적 질의가 가능하다는 장점이 있다.
또한 공개되는 데이터는 차원이 축소된 데이터에 한하여 공개하며, 해당 데이터는 클라우드 서버, 오픈 API, 공공데이터 등에 자유롭게 게시가 가능하다. 그러나 공격자가 이러한 데이터를 수집하더라도 원본 대조를 통한 재식별화 시도를 할 수 없다. 또한 고유값 및 고유벡터를 인가된 그룹에 한하여 공유하며 해당 정보를 알지 못하면 비식별화 데이터 자체를 추출할 수 없어 안전하다.
본 연구는 암호화가 아닌 비식별화 방식에 속하지만, 기존의 비식별화와 암호화의 장점을 모두 제공한다는 점에서 의의가 있다. 차원축소를 통하여 데이터의 정보를 은닉할 수 있으며, 이를 불특정 다수가 접근 가능한 클라우드 환경을 통해서도 안전하게 공유할 수 있다. 필요에 따라 정당한 권한을 가진 자는 비식별화된 데이터로 복원할 수 있다.
제안한 방식의 검증을 위해 샘플 데이터를 통한 실험 결과를 도출하였고, 안전성 및 효율성을 분석하였다. 본 논문에서 제안한 방식은 민감성이 있는 개인정보에 대하여 안전한 공유 및 빅데이터 분석 체계를 구축하는데 활용할 수 있을 것으로 기대된다. 향후 과제로 수치 데이터에 한정되지 않는 다양한 형태의 데이터에 대해 비식별화 적용이 가능한 방식을 연구하고자 한다.
References
-
D. Sánchez, M. Batet, and A. Viejo, "Utility-preserving privacy protection of textual healthcare documents", Journal of Biomedical Informatics, Vol. 52, pp. 189-198, Dec. 2014.
[https://doi.org/10.1016/j.jbi.2014.06.008]

-
J. Oh and K. Lee, "Data De-identification Framework", Computers, Materials & Continua, Vol. 74, No. 2, pp. 3579-3606, Oct. 2022.
[https://doi.org/10.32604/cmc.2023.031491]

-
A. Kovačević, B. Bašaragin, N. Milosavljevic, and G. Nenadić, "De-identification of clinical free text using natural language processing: A systematic review of current approaches", Artificial Intelligence in Medicine, Vol. 151, pp. 102845, May 2024.
[https://doi.org/10.1016/j.artmed.2024.102845]

-
Y. Xiao, S. Lim, T. J. Pollard, and M. Ghassemi, "In the name of fairness: assessing the bias in clinical record de-identification", Proceedings of the 2023 ACM Conference on Fairness, Accountability, and Transparency, Chicago IL USA, pp. 123-137, Jun. 2023.
[https://doi.org/10.1145/3593013.3593982]

-
C. C. Aggarwal and P. S. Yu, "A condensation approach to privacy preserving data mining", International Conference on Extending Database Technology, Heraklion, Crete, Greece, Vol. 2992, pp. 183-199, Mar. 2004.
[https://doi.org/10.1007/978-3-540-24741-8_12]

-
T. S. Gal, T. C. Tucker, A. Gangopadhyay, and Z. Chen, "A data recipient centered de-identification method to retain statistical attributes", Journal of Biomedical Informatics, Vol. 50, pp. 32-45, Aug. 2014.
[https://doi.org/10.1016/j.jbi.2014.01.001]

-
L. Radhakrishnan, et al., "A certified de-identification system for all clinical text documents for information extraction at scale", JAMIA Open, Vol. 6, No. 3, Oct. 2023.
[https://doi.org/10.1093/jamiaopen/ooad045]

-
K. Lee, M. Kayaalp, S. Henry, and Ö. Uzuner "A Context-Enhanced De-identification System", ACM Transactions on Computing for Healthcare (HEALTH), Vol. 3, No. 1, pp. 1-14, Oct. 2021.
[https://doi.org/10.1145/3470980]

- S. H. Chae, K. C. Kwak, and S. B. Pan, "A enhancement of the fingerprint verification using PCA", Journal of Korean Institute of Information Technology, Vol. 10, No. 5, pp. 81-89, May 2012.
- J.-W. Kim, "Face Recognition System using HWT-PCA", The Journal of Korean Institute of Information Technology, Vol. 10, No. 11, pp. 201-207, Nov. 2012.
-
B. M. Wise and N. B. Gallagher, "The process chemometrics approach to process monitoring and fault detection", Journal of Process Control, Vol. 6, No. 6, pp. 329-348, Dec. 1996.
[https://doi.org/10.1016/0959-1524(96)00009-1]


2007년 2월 : 동국대학교 전자상거래기술전공(공학석사)
2018년 2월 : 제주대학교 컴퓨터교육전공(공학박사)
2007년 6월 ~ 2008년 5월 : 한국전자통신연구원 정보보호연구단 연구원
2008년 11월 ~ 2015년 6월 : KT 플랫폼개발단 과장
2018년 3월 ~ 2021년 2월 : 제주대학교 과학기술사회연구센터 학술연구교수
2021년 3월 ~ 현재 : 청주대학교 교양학부 교수
관심분야 : 데이터 프라이버시 보호, 메타버스 보안, 지능형 영상보안, IoT 보안, AI융합교육