Equilibrium and Efficiency in Decentralized Finance: A Game-Theoretic Analysis of DeFi Pools
Abstract
The integration of Decentralized Finance(DeFi) and blockchain technology heralds a transformative shift in the financial landscape, promising unparalleled transparency, inclusivity, and efficiency. Yet, the DeFi sector faces significant challenges, primarily centered around transaction cost optimization and the alignment of incentives among diverse stakeholders. This study introduces a novel verification approach, positing that DeFi pools can inherently self-regulate and maintain equilibrium states—termed Nash equilibrium states. By utilizing mathematical formulations and simulation methodologies, this research illuminates the potential for DeFi protocols to leverage principles of game theory. It proposes ways to enhance the stability, efficiency, and fairness of protocol design within the DeFi ecosystem, thereby contributing to its advancement and robustness.
초록
분산 금융(DeFi)과 블록체인 기술의 결합은 금융 환경에서 획기적인 변화를 예고하며, 비교할 수 없는 투명성, 포괄성, 효율성을 약속한다. 그럼에도, 이 DeFi 분야는 주로 거래 비용 최적화와 다양한 이해 관계자의 인센티브 조정과 같은 중대한 도전에 직면하고 있다. 본 연구는 DeFi 풀이 내쉬 균형상태라는 새로운 검증 방식을 도입하여, DeFi 풀이 본질적으로 자체 규제하고 균형 상태를 유지할 수 있다는 가설을 검증하고자 한다. 수학적 표현과 시뮬레이션의 구현 방법을 통해, DeFi 프로토콜이 게임 이론의 원리를 활용할 수 있는 가능성을 밝혀내며, DeFi 생태계 내에서 프로토콜 설계의 안정성, 효율성, 공정성을 향상시키기 위한 방안을 제시한다.
Keywords:
DeFi, nash equilibrium, game theory, tokeneconomy, blockchain technology, gas feeⅠ. Introduction
The nascent Decentralized Finance(DeFi) sector is not without its challenges. Two primary obstacles—optimizing gas fees and aligning the disparate incentives of stakeholders—loom large, posing significant threats to the scalability and adoption of DeFi platforms, particularly those built on the Ethereum[1] blockchain. This paper posits that DeFi liquidity pools are pivotal to the DeFi ecosystem and can be modeled using Nash equilibrium[2][3], where the interplay of stakeholders—Liquidity Providers, traders, and arbitrageurs—forms a strategic game that regulates itself when designed correctly. The study employs both mathematical formalism and computational simulation to explore the feasibility of achieving Nash equilibrium in DeFi pools. Through game-theoretical modeling, it assesses the conditions that facilitate equilibrium, aiming to resolve conflicts and optimize outcomes. The agent-based computational simulations provide practical insights by replicating the dynamic interactions within a DeFi setting.
Integrating economic theory with computer science methods, this research advances the understanding of how DeFi pools can organize themselves into stable and sustainable configurations, offering significant theoretical and practical contributions to the governance and design of DeFi protocols. By determining the conditions for Nash equilibrium, the paper supports ongoing efforts to improve the efficiency, fairness, and sustainability of the DeFi sector, pushing forward the potential of decentralized financial systems.
Ⅱ. Related Work
In the section discussing Decentralized Finance (DeFi), key research focuses on the design of DeFi pools, game theory, and challenges inherent in Ethereum Improvement Proposal 1559 (EIP-1559)[4]. The paper "Base Fee Manipulation In Ethereum's EIP-1559 Transaction Fee Mechanism"[5] highlights the potential for base fee manipulation by miners under EIP-1559[4], raising concerns about the achievement of Nash equilibrium and implications for blockchain security. Further examined in "Empirical Analysis of EIP-1559: Transaction Fees, Waiting Times, and Consensus Security"[6], the minimal impact of EIP-1559[4] on reducing gas fees is discussed alongside the increase in miner extractable value(MEV) and associated security risks. Tim Roughgarden's "Transaction Fee Mechanism Design for the Ethereum Blockchain: An Economic Analysis of EIP-1559"[7] critiques the game-theoretic outcomes of EIP-1559[4], emphasizing its limited effectiveness in fee reduction and the potential for miner collusion. Additional vulnerabilities, such as susceptibility to sandwich attacks facilitated by the protocol's features, are addressed in "A Study on Blockchain Sandwich Attack Strategies Based on Mechanism Design Game Theory"[8] and further explored in Patrick Züst’s "Analyzing and Preventing Sandwich Attacks in Ethereum"[9]. P. Züst et al. proposes strategies to mitigate these risks. "Eliminating Sandwich Attacks with the Help of Game Theory"[10] advocates for a redesign of DeFi pools using game-theoretic principles to ensure fairness and security under EIP-1559[4]. Collectively, these studies stress the necessity of incorporating robust game-theoretic frameworks and Nash equilibrium in the design of DeFi pools, aiming to enhance the overall security, fairness, and efficiency of the DeFi ecosystem.
These studies highlight the use of Nash equilibrium in optimizing DeFi pool designs, focusing on participant interaction and system balance. This approach offers design principles that ensure both efficiency and stability in DeFi pools, thereby contributing significantly to the growth of the decentralized financial ecosystem.
Ⅲ. DeFi Pool Modeling
Our study applies game theory and mechanism design to model strategic interactions within DeFi pools, demonstrating the potential to reach Nash equilibrium where no participant benefits from changing their strategy independently. This theoretical framework helps elucidate the conditions under which DeFi pools can operate optimally and equitably, enhancing overall ecosystem stability.
3.1 Define interactions in a DeFi pool
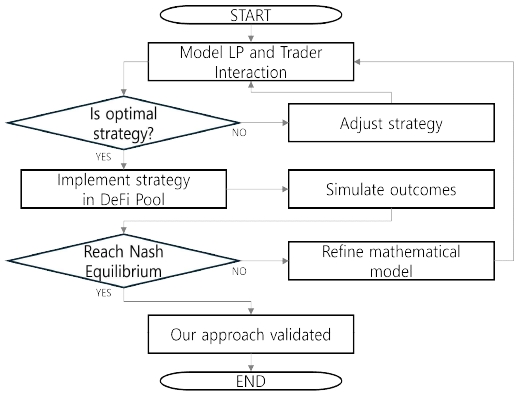
To articulate the dynamics of DeFi pools, we model the interaction of participants as a non-cooperative game, wherein each participant seeks to maximize their utility through the strategic selection of actions. The fundamental premise is that DeFi pools can achieve a state of Nash equilibrium[2][3], where no participant has an incentive to unilaterally deviate from their chosen strategy, given the strategies of all other participants. The Figure 1, a proposal to optimize gas fees and align incentives within DeFi protocols using game-theoretic principles.
It starts with the modeling of interactions between Liquidity Providers and traders, assessing whether the devised strategy is optimal. If not, adjustments are made to the strategy, which is then re-evaluated. Once an optimal strategy is identified, it is implemented in the DeFi pool for simulation. The process aims to reach a Nash equilibrium, validating the framework. If the Nash equilibrium is not achieved, the mathematical model is refined, and the process iterates until the framework's effectiveness is confirmed.
Let participants are Liquidity Providers(LPs) and Traders, and strategy space is that Liquidity Providers can choose to offer their assets to DeFi pools, and traders can choose a strategy to use these pools to exchange specific assets. Payoff function is the participant's payoff(profit) depends on the selected strategy. Each participant chooses a strategy that maximizes his or her payoff. The strategy profile of a game is the set of strategies of all participants. Let be the strategy space Li of Liquidity Providers i, and the strategy space Ti of the trader. We cite the equilibrium state proof in game theory previously performed by John Nash. DeFi Pool is one of the inevitable models that achieves a state of balance among multiple participants.
The following Table 1 shows the corresponding variables and expressions between the variables used by Nash when he proved the Nash equilibrium[2][3], the notation used by several studies on the Nash equilibrium, and the notation used in our paper.
Based on given expressions, Liquidity Provider i' s payoff:
| (1) |
is the total trading volume through the pool.
In a Nash equilibrium, this strategy profile forms a fixed point:
| (2) |
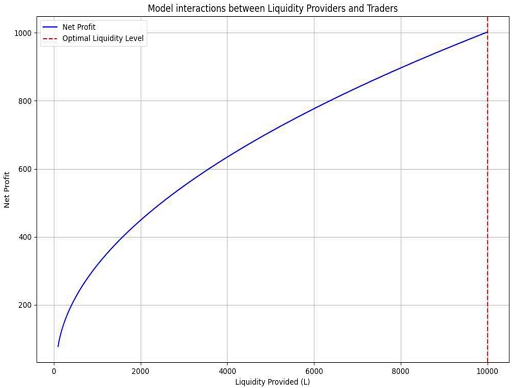
Equation (2) is Nash equilibrium condition implementation. A Nash equilibrium is a strategy profile where, for any participant, given the strategies of all other participants, changing their own strategy can no longer improve the payoff. And assumption is the strategy space Li of Liquidity Providers is a finite, closed convex set. We simulated and visualized the net profit according to the liquidity provided by Liquidity Providers in DeFi pools using algorithm-based source code as Figure 2.
We calculated the net profit for each level of liquidity within the range of liquidity L and plot it on a Figure 2. A red dotted vertical line representing the liquidity level at which net profit is maximized has been added to provide Liquidity Providers with a visual representation of the optimal liquidity level. This Figure 2 is a useful tool for understanding the behavior of DeFi pools and exploring how Liquidity Providers can maximize profits. Model the complex incentives and consequences of liquidity provision, including variable trading fees, liquidity mining rewards, and price impact costs.
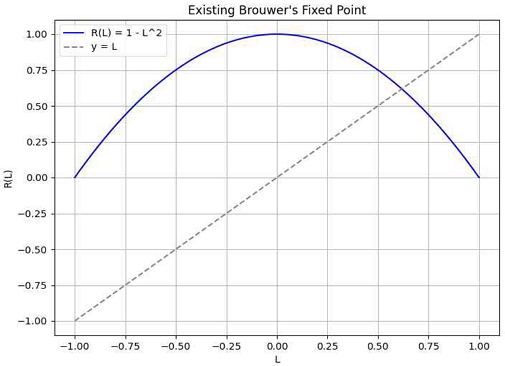
The payoff function Pi(Li, L-i) is continuous for each Liquidity Provider i and is defined over its strategy space. According to Brouwer's fixed point theorem, if every continuous function f maps to S within a closed convex set S, then f has at least one fixed point. In other words, there exists x ∈ S that satisfies f(x) = x. We define the optimal response function of each Liquidity Provider as Ri(L-i). This function returns the optimal strategy of Liquidity Provider i, given the strategies L-i of all other Liquidity Providers. We defined the overall optimal response function:
| (3) |
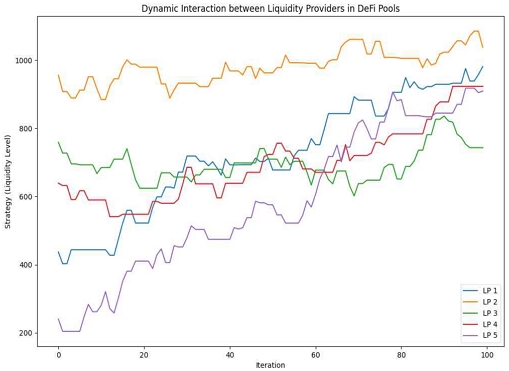
By equation (4), there is at least one fixed point (Nash equilibrium). This represents the optimal response of the entire system to the strategies of all Liquidity Providers. R constructs a continuous mapping from a closed convex set to itself. Therefore, according to Brouwer's fixed point theorem, there exists at least one fixed pointL* that satisfies R(L) = L. At L*, any Liquidity Provider can no longer increase the payoff by changing its strategy. Therefore, this represents the Nash equilibrium of the game. Figure 3 proofs process ensures the existence of a Nash equilibrium in modeling the interactions between Liquidity Providers.
Using Brouwer's fixed point theorem, we prove that a Nash equilibrium of the game exists in DeFi pool. We define the optimal response function of each Liquidity Provider and show that the common fixed point of these functions is the strategy profile that represents the Nash equilibrium of the game.
To implement a more accurate simulation showing the existence of a Nash equilibrium based on equation (3), we need to define the optimal response function of each Liquidity Provider and find a common fixed point for these functions. This involves using Brouwer's fixed point theorem to show that a Nash equilibrium for the system as a whole exists when each Liquidity Provider chooses its optimal strategy in Figure 4, taking into account the strategies of all other Liquidity Providers.
3.2 Threats to validity
The analysis establishes that under a well-defined framework of rules and incentives, DeFi pools can achieve a Nash equilibrium, where no participant gains by unilaterally changing their strategy. This state not only exemplifies the potential for efficient and equitable operation of DeFi pools but also optimizes outcomes for all stakeholders. It highlights the role of equilibrium in stabilizing pools, enhancing liquidity, and reducing transaction costs, thereby aiding ecosystem scalability. The study also considers the resilience of the DeFi pool model against market fluctuations and operational efficiency. However, it notes limitations such as oversimplified models that may not capture the complex dynamics of actual DeFi environments, potential discrepancies from computer simulations, and the exclusion of factors like impermanent loss and regulatory impacts. The diversity in DeFi protocols indicates that Nash equilibrium conditions may vary across different platforms. Future research will explore gas cost minimization within these equilibria and extend findings to generalized DeFi pools maintaining Nash equilibrium.
Ⅳ. Conclusion
DeFi transcends technological innovation, aiming to revolutionize the financial system through a synergy of technological prowess, user-centric design, sustainable growth, and global collaboration. This study confirms DeFi's potential to enhance global financial inclusion and forge a more equitable and efficient financial ecosystem. If stakeholders unite behind this vision, DeFi can lead to a sustainable and innovative financial future, not just in terms of technology, but also in expanding financial access, enhancing market efficiency, and fostering transparency and trust. DeFi stands to surmount traditional finance limitations, offering tangible economic opportunities worldwide. It is reshaping the financial future with endless possibilities through its novel approach to financial services. This study's model and analysis provide a foundational understanding of DeFi pools, illustrating their ability to achieve Nash Equilibria that maximize participant welfare. With mathematical proof of these pools' convergence toward equilibrium, we present a framework for creating DeFi protocols that are equitable, efficient, resilient, and sustainable amidst changing market conditions and participant actions, contributing substantially to the discourse on the future of decentralized financial systems.
Acknowledgments
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government (MSIT) (No. RS-2023-00251241) and also supported by Kyonggi University’s Graduate Research Assistantship 2024.
References
- https://ethereum.org/ko/whitepaper/, [accessed: Feb. 01, 2024].
-
J. F. N. Jr, "Equilibrium points in n-person games", Proceedings of the National Academy of Sciences, Vol. 36, No. 1, pp. 48-49, Jan. 1950.
[https://doi.org/10.1073/pnas.36.1.48]
-
J. Nash, "Non-cooperative games", Annals of Mathematics, Vol. 54, No. 2, pp. 286-295, Mar. 1951.
[https://doi.org/10.2307/1969529]
- https://eips.ethereum.org/EIPS/eip-1559, [accessed: Feb. 01, 2024].
- S. Azouvi, G. Goren, L. Heimbach, and A. Hicks, "Base Fee Manipulation In Ethereum's EIP-1559 Transaction Fee Mechanism", arXiv preprint arXiv:2304.11478, , Apr. 2023.
-
Y. Liu, Y. Lu, K. Nayak, F. Zhang, L. Zhang, and Y. Zhao, "Empirical analysis of EIP-1559: Transaction fees, waiting times, and consensus security", Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pp. 2099-2113, Nov. 2022.
[https://doi.org/10.1145/3548606.3559341]
- T. Roughgarden, "Transaction fee mechanism design for the Ethereum blockchain: An economic analysis of EIP-1559", arXiv preprint arXiv:2012.00854, , Dec. 2020.
-
Y. Liang, X. Wang, Y. C. Wu, H. Fu, and M. Zhou, "A Study on Blockchain Sandwich Attack Strategies Based on Mechanism Design Game Theory", Electronics, Vol. 12, No. 21, p. 4417, Nov. 2023.
[https://doi.org/10.3390/electronics12214417]
- P. Züst, T. Nadahalli, and Y. W. R. Wattenhofer, "Analyzing and preventing sandwich attacks in Ethereum", ETH Zürich, Aug. 2021.
-
L. Heimbach and R. Wattenhofer, "Eliminating sandwich attacks with the help of game theory", Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security, Nagasaki Japan, pp. 153-167, May 2022.
[https://doi.org/10.1145/3488932.3517390]

2020. 2 : Bachelor’s Degree in Computer Science from Kyonggi University
2022. 2 : Master’s Degree in Computer Science from Kyonggi University
2022. 3 ~ present : Ph.D. Candidate in Computer Science at Kyonggi University
Research interests: Blockchain, Cybersecurity

2005 : Bachelor’s Degrees in Mathematics and Computer Science & Engineering from Korea University
2007 : Master’s Degree in Computer Science & Engineering from Korea University
2012 : Ph.D. in Computer and Communications Engineering from Korea University
2012 ~ 2018 : Senior Researcher at the Agency for Defense Development
2018 ~ present : Professor of Computer Engineering at Kyonggi University's School of AI Computer Engineering
Research interests : Cybersecurity, Blockchain, Malware Analysis