딥 러닝 기반 미상 레이다 대응 재밍 알고리듬

Ⅰ. 서 론

전자공격은 적의 전파의 사용을 제한하거나 무력화시키는 것으로 현대전에서는 아군의 성공적인 임무에 필수적이다. 특히 항공기나 함정의 자체보호 장비의 재밍은 추적 레이다나 미사일에 대한 대응 방법중 하나로 아군의 생존성을 향상시키고 작전효과도를 높인다[1][2]. 수신된 위협 신호의 특성에 따라 재밍효과가 다르므로 다양한 위협 신호에 대하여 적절한 재밍기법을 적용하는 것이 필요하다.

일반적으로 재밍기법은 장기간 수집된 신호분석을 통해 HILS(Hardware In-the-Loop System) 또는 M&S(Modeling and Simulation)를 활용하여 전문가에 의해 선정된다. 선정된 재밍기법은 임무 전에 위협별로 매칭되어 재머에 라이브러리 형태로 저장된다. 위협 신호가 라이브러리에 존재하는 경우에는 쉽고 빠르게 재밍기법을 적용할 수 있지만, 레이다의 모드 변경이나 장비의 측정오차 등에 의해 기존과 변형된 위협신호로 수신되는 경우에 라이브러리 방식은 미상 신호로 인식하여 적절한 재밍기법을 찾는데에 한계가 있다. 그러나, 기계학습 기법을 활용하여 위협의 제원과 재밍기법에 대한 추정 모델을 학습하면 미상의 신호에 대해서도 학습한 모델을 이용하여 가장 유사한 위협신호 패턴에 대한 재밍기법을 추정함으로써 기존 방식보다 큰 재밍효과를 기대할 수 있다.

본 논문에서는 미상의 레이다 신호에 대한 재밍기법 추정을 위해 동시발생 행렬을 사용한 딥 러닝 기반의 재밍기법 추정방법을 제안한다. 영상 분야에서 텍스쳐 분석에 주로 사용되는 동시발생 행렬은 이미지에 대해 주어진 오프셋에서 동시 발생 픽셀 값의 분포로 정의되는 행렬이다. 시계열의 특징을 갖는 위협 특성을 잘 분리하기 위해 공간적 분석 방법인 동시발생 행렬을 주파수와 펄스반복주기(PRI, Pulse Repeatition Interval)에 대해 구성하여 딥 러닝 모델로 학습하고 10 폴드 방식으로 10번의 미상 신호에 대한 성능을 동시발생 행렬을 사용하지 않았을 때와 비교하여 평가하였다.

실제 신호환경에서는 학습시와는 달리 위협 신호의 수집 PDW(Pulse Description Word) 개수가 충분하지 못한 경우가 많다. 제안한 알고리듬에 대해 수집된 PDW의 개수에 따른 성능도 실험을 통해 평가하였다.

본론에서 기존 라이브러라 방식과 제안된 동시발생 행렬의 특징을 이용한 딥 러닝 기반 재밍 알고리듬에 대해 설명하고, 실험 결과에서 제안된 알고리듬과 미상 신호에 대한 성능을 전자전에서 많이 사용하는 일반적인 모멘트를 특징으로 사용하였을 때의 결과와 비교한다. 또한 실제 환경에서의 적용성을 검증하기 위해 수집 PDW 양에 따른 성능을 분석하고 결론을 맺는다.

Ⅱ. 본 론

2.1 기존 라이브러리 방식의 미상신호 대응 방법 및 기존 전자전에서의 특징

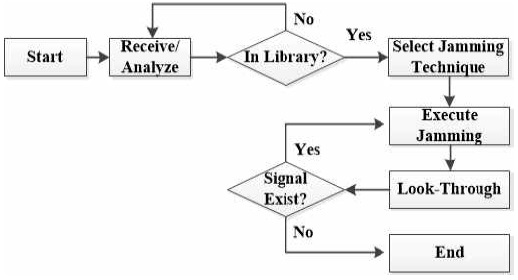
그림 1은 분석된 위협에 대해 사전에 재밍기법을 선정하여 라이브러리에 저장하여 사용하는 재머의 일반적인 재밍절차이다. 재머에 수신, 분석된 신호가 라이브러리에 존재하는 위협이면 라이브러리로부터 재밍기법을 선택하고 재밍을 수행한 경우 룩-쓰루(Look-through)를 통해 신호가 존재하는 지를 판단하여 재밍지속 또는 재밍기법 변경을 통해 재밍을 수행한다. 재머에 수신된 신호가 라이브러리에 존재하지 않는 미상으로 인식된 경우에는 재밍기법이 할당되어 있지 않기 때문에 기본적으로 재밍을 수행하지 않는다. 다만, 장비에 따라 운용자 선택에 따라 잡음 재밍을 강제로 방사하게 하는 경우도 있으나 이는 재밍효과를 크게 기대하기 어렵다.

Fig. 1.

Flow chart of conventional jammer

그림 1에서와 같이 재머는 수신된 신호에 대해 분석을 수행한다. 이때 다양한 방법을 이용하여 레이다 신호 식별을 수행한다. 근래에는 기계학습 기법을 이용하여 펄스간, 펄스내 분석을 수행하는데 일반적으로 주파수와 시간축에서의 신호 특성을 분석하고 이로부터 특징을 추출하여 학습 및 분류를 수행한다[3].

[4]-[6]에서와 같이 주파수 변조, PRI 변조 및 펄스폭 특성에 대해 수식 (1)~(5)처럼 다양한 모멘트를 특징을 레이다 신호 분류에 사용한다.

$\[ Mean\left(\mu \right)=E\left[\left(X\right)\right] \]$

(1)

$\[ Variance=E\left[{\left(X-\mu \right)}^2\right] \]$

(2)

$\[ StandardDeviation\left(\sigma \right)=\sqrt{E\left[{\left(X-\mu \right)}^2\right]} \]$

(3)

$\[ Skewness=E\left[{\left(\frac{X-\mu }{\sigma }\right)}^3\right] \]$

(4)

$\[ Kurtosis=E\left[{\left(\frac{X-\mu }{\sigma }\right)}^4\right] \]$

(5)

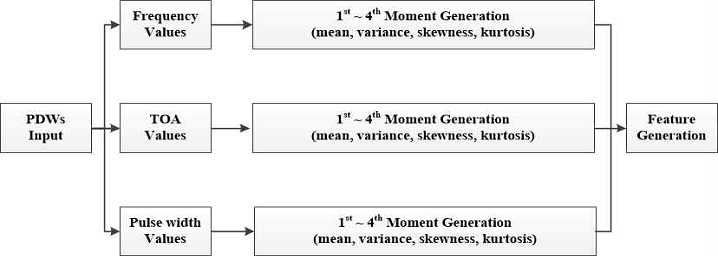
그림 2는 주파수, PRI, 펄스폭에 대해 기존 전자전분야에서 주로 사용되는 모멘트를 특징으로 추출하여 사용할 경우의 흐름도이다.

Fig. 2.

Conventional features in electronic warfare

2.2 동시발생 행렬을 이용한 특징추출 알고리듬

본 논문에서는 단순 레이다 데이터 분석과 함께 미상의 레이다 신호에 대한 재밍기법을 예측하기 위해 동시발생 행렬을 이용한 특징추출 알고리듬과 그 특징을 이용한 딥러닝 알고리듬을 제안한다.

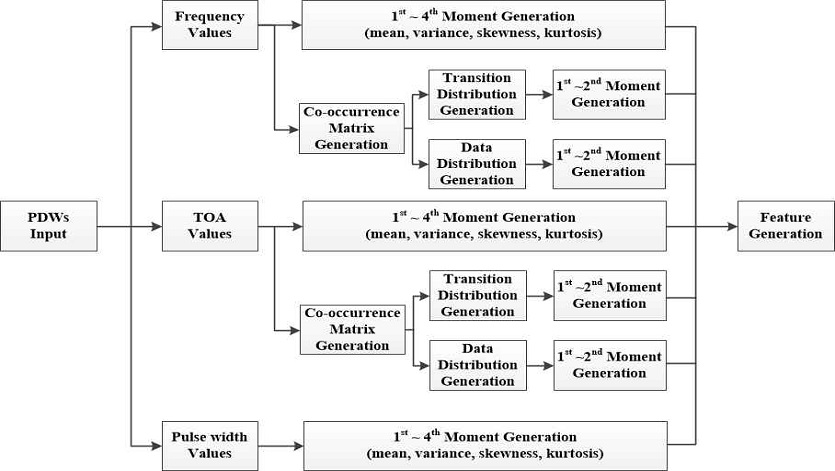
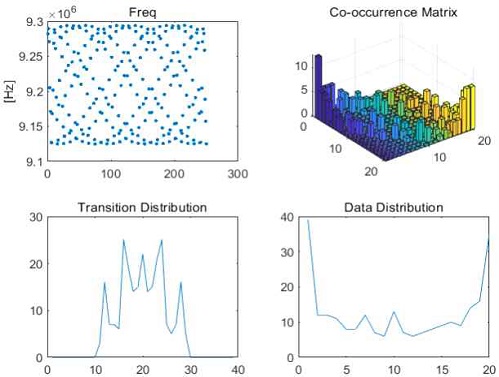
동시발생 매트릭스는 시계열의 레이다 데이터를 공간적 특징으로 변환하는 것으로 그림 3은 미상 레이다 신호에 대한 재밍기법 예측을 위해 동시발생 매트릭스를 사용한 특징 추출 알고리즘이다.

Fig. 3.

Proposed feature extraction using co-occurrence matrix

기존 연구들에서 많이 사용한 n차 모멘트와 함께 PRI와 주파수에 대해 동시 발생 행렬을 사용하였다. 제안한 알고리듬은 기존 모멘트 특징과 함께 주파수와 TOA에 대해 동시발생 행렬을 생성하여 천이 및 데이터 분포에 대한 1, 2차 모멘트를 특징으로 추출하여 적용였다. 추출된 특징들은 정규화하여 심층신뢰망(DBN, Deep Belief Network)[7]의 입력으로 사용한다.

동시발생 행렬은 일반적으로 동시발생 픽셀수를 통한 이미지 분석 또는 시계열 데이터를 공간적 분석을 위한 분포로 변환하는 그레이 레벨 동시발생 행렬(GLCM, Gray Level Co-occurrence Matrix)로 식 (6)과 같이 정의한다[8].

$\[ \begin{array}{c}{C}_{\Delta x,\Delta y}\left(i,j\right)= \hfill \\ \sum _{x=1}^n\sum _{y=1}^m\left\{\begin{array}{cc}1\hfill & \text{if} I\left(x,y\right)=i \text{and} I\left(x+\Delta x,y+\Delta y\right)=j\\ 0,\hfill & otherwise\end{array}\right.\hfill \end{array} \]$

(6)

여기서 i와 j는 픽셀 값, x와 y는 n×m의 이미지 I에서의 공간적 위치이다. 옵셋 (Δx, Δy)는 이 행렬이 계산되는 공간 관계를 정의한다. I(i, j) 는 픽셀 (x, y)의 픽셀 값을 나타낸다.

본 논문에서는 식 (6)에 따라 주파수와 펄스반복간격(PRI)에 대한 동시발생 행렬을 생성한다. N, M은 주파수 대역폭이고 c는 인접 주파수 대역폭에서 생성되는 주파수 값이다. 동시발생 행렬은 정량화된 값을 정규화하여 생성한다.

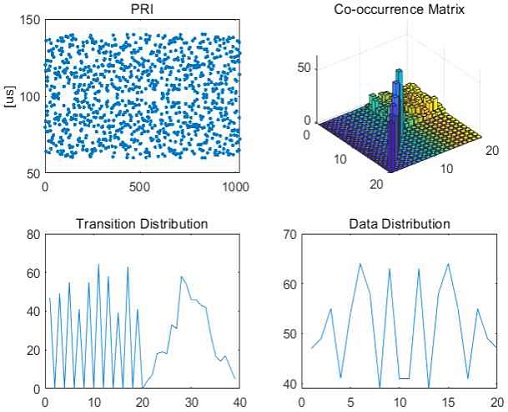
생성된 동시발생 행렬에서 천이 및 데이터 분포를 생성한다. 천이 분포는 대각선 방향의 marginal PMF를 계산하여 값의 변화를 분석한 그래프이고, 데이터 분포는 가로 방향의 marginal PMF를 계산한 후 값의 변화를 분석한 그래프이다. 본 논문에서는 주파수, PRI에 대해 천이 및 데이터 분포의 1, 2차 모멘트, 평균과 분산을 특징으로 추출한다.

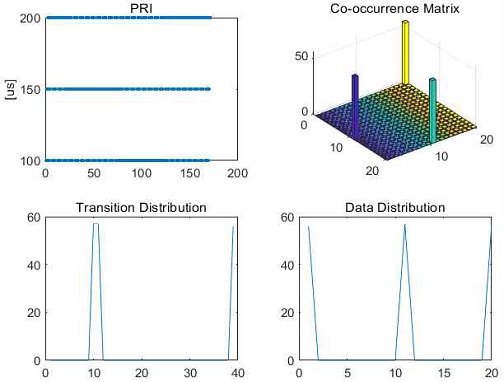
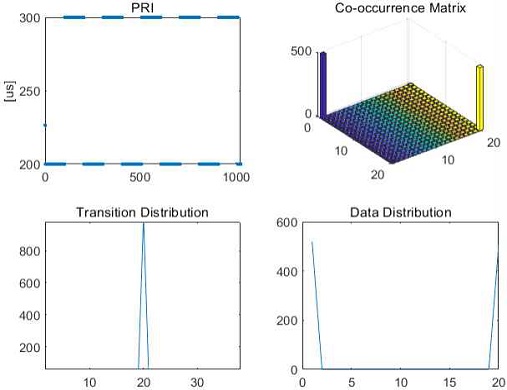
그림 4, 5, 6은 주요 PRI 형태인 지터, 스태거, D&S(Dwell and Switch)에 대한 샘플 및 그에 대한 동시 발생 행렬과 천이, 데이터 분포의 예이다.

Fig. 4.

Jitter PRI co-occurrence matrix, transition distribution and data distribution

Fig. 5.

Staggered PRI co-occurrence matrix, transition distributiona and data distribution

Fig. 6.

D&S co-occurrence matrix, transition distribution and data distribution

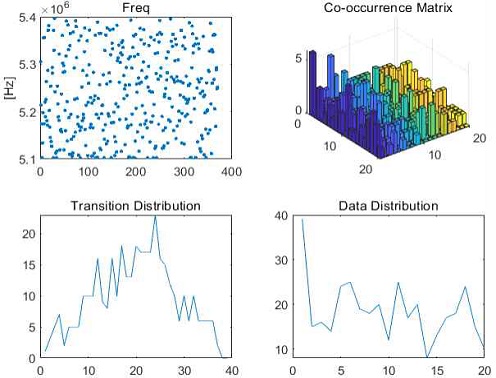
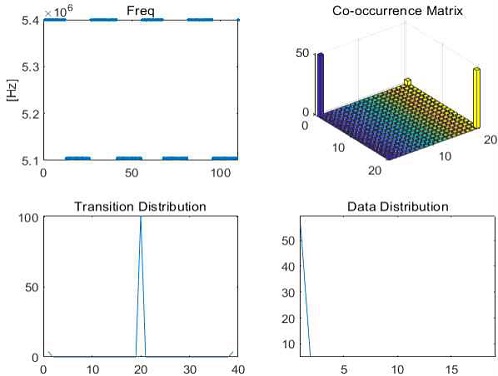
그림 7, 8, 9는 어자일 및 호핑, 패턴화된(Sine) 주파수 변조 형태에 대한 샘플 신호와 그에 대한 동시 발생 행렬과 천이, 데이터 분포의 예이다.

Fig. 7.

Agile frequency co-occurrence matrix, transition distribution and data distribution

Fig. 8.

Hopping frequency co-occurrence matrix, transition distribution and data distribution

Fig. 9.

Patterned(sine) frequency co-occurrence matrix, transition distribution and data distribution

2.2 재밍기법 예측 모델

딥러닝 알고리듬의 일종인 DBN을 이용하여 미상의 레이다에 대해 재밍기법을 예측하는 모델을 제안한다. 일반적으로 추출된 특징이 아닌 데이터 자체를 학습하는 딥러닝 알고리듬이 대중화되어 있지만 이는 학습 시간이 길다는 단점이 있다. 따라서 재밍기법 예측기는 DBN의 딥 러닝 모델을 선택할 때 CNN(Convolutional Neural Network) 또는 LSTM(Long Short-Term Memory)에 비해 학습 속도 인식 속도가 충분히 향상되도록 설계하였다[9]. [10]에 따르면 DBN의 학습 속도는 LSTM의 학습 속도보다 1.79배 이상 높다.

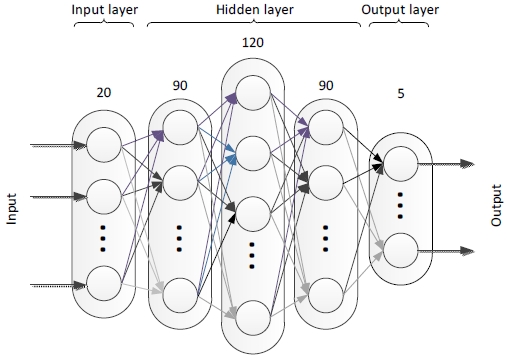
위의 알고리듬을 적용하여 개발한 미상 레이다의 재밍기법 예측을 위한 DBN 모델의 구조는 그림 10과 같다. 입력 계층은 특징 추출 알고리듬에 의해 추출된 20개의 특징을 수신하는 20개의 노드로 구성된다. 특징은 주파수, PRI 및 PW의 1~4번째 모멘트에서 획득한 12개의 값과 동시 발생 행렬의 천이 및 데이터 분포의 평균 및 분산에서 획득한 8개의 값이 있다. 3개의 은닉 레이어가 있으며 각 레이어에는 각각 90, 120, 90개의 노드로 구성한다. 5개의 출력이 있는 출력 레이어는 SoftMax를 연결하고 출력값을 신뢰도로 변환한다.

Fig. 10.

DBN structure for jamming against unknown radar signal

III. 실험 결과

미상 위협에 대해 제안된 알고리듬의 성능을 평가하였다. 학습 및 테스트를 위한 데이터 세트는 각 레이다의 PDW 목록에 재밍기법으로 레이블링하여 구성하였다. 재밍기법은 잡음, 기만, 복합재밍 기법 중 5가지 재밍기법을 선택하였다[11].

PDW 목록은 주파수 및 PRI 변조와 같은 다양한 신호를 포함하는 2,000개 이상의 레이다 모델로부터 생성하였다[12]. PRI 변조 형태는 고정, 스태거, D&S, 지터 및 패턴이 있다. 주파수 변조 형태에는 고정, 호핑, 어자일 및 패턴이 있다.

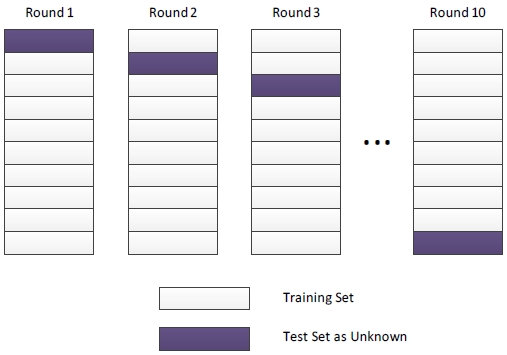
각 목록에는 최소 1,000개에서 최대 9,000개의 PDW를 포함한다. 이 실험에 사용된 위협은 전체 테스트 데이터 세트를 10 등분하여 9개는 학습용으로 사용하고 다른 하나는 미상 위협으로 설정하여 테스트 데이터로 사용하였다. 각 폴드에서 5개의 재밍기법은 1, 2, 3, 4 및 5로 각각 약 50%, 16%, 20%, 9% 및 5%로 레이블로 지정하였다.

실험은 성능은 인식률로 산출하였으며, 실험당 약 150,000 - 190,000개의 알려지지 않은 위협 데이터 세트가 테스트로 사용되었다. 각 테스트 케이스에 대한 데이터 세트 구성은 그림 11과 같다.

Fig. 11.

Data configuration and method for each test case

본 논문에서 제안한 알고리듬의 성능을 비교하기 위해 그림 2와 같이 전자전분야에서 많이 사용하는 특징, n차 모멘트를 그림 11의 DBN 구조의 입력으로 설정하여 비교하였다.

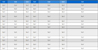
표 1에서 보듯이 두 가지 방법 모두 잘 학습되었음을 알 수 있다. 그러나, 표 2에서 보듯이 미상 레이다 신호에 대한 재밍기법 예측는 본 논문에서 제안한 동시발생 행렬을 특징으로 이용한 알고리듬으로 미상신호에 대한 재밍기법을 예측하였을 때 98.15%로 일반적인 특징을 사용하였을 때보다 약 14%가량 좋은 성능을 보였다.

Table 1.

Comparing learning and validation result

Table 2.

Unknown threat results with the proposed method and conventional feature method

이는 제안한 방법을 이용하였을 때 미상의 레이다 신호에 대해서 기존 재머의 방식이나 일반적인 특징을 이용할 때보다 신뢰성 있게 재밍이 가능하여 재머의 효과를 높일 수 있다고 볼 수 있다.

재머가 실제로 동작하는 상황에서는 다양한 환경 때문에 학습에 사용한 데이터만큼 위협 데이터가 수집되지 못하는 경우가 많다. 이러한 상황 하에서 제안한 알고리듬의 성능을 평가하기 위해 PDW 데이터 개수를 학습시 사용한 것 대비 70%, 50% 20%, 10%까지 낮춰 실험을 수행하였다. 표 3에서 보듯이 학습 PDW 개수 대비 10%인 상황에서도 약 88%의 확률로 재밍기법을 잘 예측함을 보였다.

Table 3.

Test result by number of test PDW

IV. 결론 및 향후 과제

본 연구에서는 라이브러리에 존재하지 않는 미상 위협 신호에 대해 재밍기법을 예측하는 새로운 방법을 제안하였다. 딥러닝 알고리듬과 연계하여 5가지 유형의 재밍기법을 사용하여 미상 신호의 특징을 추출하는 동시 발생 행렬 및 미상 신호에 대한 레이다 재밍기법 분류를 제안하였다.

동시발생 행렬을 특징으로 이용한 DBN 기반 딥러닝 알고리듬과 일반적인 모멘트를 특징으로 사용하였을 때의 성능을 비교, 검증하였다. 제안한 알고리듬은 미상 위협에 적절히 대응하지 못하는 기존의 방법과 달리 미상 위협에 대해 98%의 확률로 재밍기법을 예측함을 보였다. 또한, 기존 전자전에서 사용하는 모멘트를 사용할 때보다 14% 성능이 나아짐을 볼 수 있었다. 또한, 제안한 알고리듬은 학습시 사용한 PDW 개수 대비 10%만 수신되었더라도 88%이상 확률로 재밍기법을 잘 예측함을 보였다.

향후 추가적으로 본 알고리듬을 실제 장비에 탑재하여 성능 검증이 이루어진다면, 기존 재머의 단점을 보완하는 신규 재머 장비가 개발될 수 있을 것으로 기대한다.

References

• M. I. Skolnik, "Introduction to RADAR Systems, 3rd edition", Tata McGraw-Hill publishing company limited. Singapore, pp. 547, Dec. 2002.
• L. Neng-Jing and Z. Yi-Ting, "A survey of radar ECM and ECCM", IEEE Trans. Aerosp. Electron. Syst., Vol. 31, No. 3, pp. 1–6, Jul. 1995. [https://doi.org/10.1109/7.395232]
• G. Noone, "A neural approach to automatic pulse repetition using convolutional neural network", ICONIP'99. ANZIIS'99 & ANNES'99 & ACNN'99. 6th International Conference on Neural Information Processing, Proceedings (Cat. No.99EX378), Perth, WA, Australia, Vol. 3, pp. 213-218, Nov. 1999.
• C. M. Jeong, Y. G. Jung, and S. J. Lee, "Neural network-based radar signal classification system using probability moment and ApEn", Soft Comput., Vol. 22, No. 13, pp. 4205–4219, 2018. [https://doi.org/10.1007/s00500-017-2711-7]
• J. Kauppi and K. Marikainen, "An efficient set of features for pulse repetition interval modulation recognition", in Proc. IET Intl. Conf. on Radar Systems, Edinburgh, UK, Oct. 2007. [https://doi.org/10.1049/cp:20070548]
• X. Li, Z. Huang, F. Wang, X. Wang, and T. Liu, "Toward convolutional neural networks on pulse repetition interval modulation recognition", IEEE Commun. Lett., Vol. 22, No. 11, pp. 2286–2289, Nov. 2018. [https://doi.org/10.1109/LCOMM.2018.2864725]
• G. E. Hinton, S. Osindero, and Y.-W. Teh, "A fast learning algorithm for deep belief nets", Neural Comput., vol. 18, no. 7, pp. 1527–1554, 2006. [https://doi.org/10.1162/neco.2006.18.7.1527]
• R.M.Haralick, K. Shanmugam, and I. Dinstein, "Textural Features for Image Classification", IEEE Transactions on Systems, Man, and Cybernetics, Vol. 3, No. 6, pp. 610–621, 1973, Nov. 1973. [https://doi.org/10.1109/TSMC.1973.4309314]
• K. Cao et al., "CNN-LSTM coupled model for prediction of waterworks operation data", Int. J. Inf. Process. Syst., Vol. 14, No. 6, pp. 1508–1520, Dec. 2018.
• G. H. Lee, J. Jo, and C. H. Park, "Jamming prediction for radar signals using machine learning methods", Secur. Commun. Netw., Vol. 2020, pp. 1-9, Jan. 2020. [https://doi.org/10.1155/2020/2151570]
• C. Schleher, Introduction to Electronic Warfare. Artech House, 1986.
• J. L. Eaves and E. K. Reedy, Principles of Modern Radar. Van Nostrand Reinhold, 1987. [https://doi.org/10.1007/978-1-4613-1971-9]