인공위성 추적을 통한 지상 장거리 레이다 성능 검증

Ⅰ. 서 론

최근 다기능 레이다는 다수의 배열 반도체 송수신모듈이 결합한 형태의 능동위상배열 레이다로 구현되고 있다[1]. 능동위상 배열 레이다는 다수의 배열 모듈을 합성한 빔을 전자적으로 제어하기 때문에 고각, 방위각, 주파수, 빔 형성 오차에 따라 조향 오차가 발생할 수 있다[2]. 이러한 빔 조향 오차 문제를 해결하기 위해 개발 단계에서 근전계 및 원전계 측정 시설을 이용해 레이다의 안테나 빔을 측정하고 보정을 수행한다[3]. 그러나, 일반적으로 근전계 및 원전계 측정은 이상적인 실험실 환경이나 제한된 시설 환경에서 진행된다. 따라서 예측하기 힘든 다양한 환경 요소 등이 존재하는 실 환경에 레이다가 배치된 후 성능이 열화되는 경우가 종종 발생한다. 또한 능동위상배열 레이다의 경우 배열 반도체 송수신모듈의 고장에 따라 모듈 교체가 빈번하게 발생하므로, 주기적으로 빔의 출력 및 정렬을 검증하는 방법이 요구된다[4]. 점검을 위해 검교정 시설로의 이동을 고려할 수 있으나, 장거리 레이다는 안테나 크기 및 중량 때문에 이동이 쉽지 않고, 측정 시설로 옮긴다고 할지라도 측정에 드는 시간 및 비용이 상당하므로, 전력에 공백이 발생할 수 있다. 따라서 배치된 상태에서 레이다의 상태를 효과적으로 점검하는 방안이 필요하다.

장거리 레이다는 점점 더 원거리에서 목표물을 탐지/추적할 수 있도록 개발되는 추세이고, 또한 원거리에서 표적 추적 오차를 최소화하기 위해 더 높은 수준의 레이다 정렬 정확도 성능을 요구하고 있다[5]. 장거리 레이다는 안테나 장치의 크기가 크고, 장치의 무게가 무거우므로 기구 제어를 통해 정확하게 자세를 제어하는 게 어렵다. 따라서 정밀한 자세 측정 센서가 추가되어 장비의 자세를 정확하게 측정 및 처리해야 한다. 또한 표적의 탐지/추적 거리가 상대적으로 멀기 때문에, 안테나 자세의 미세한 틀어짐이 원거리 표적의 거리/각도의 큰 오차를 일으키기 때문에 높은 수준의 정렬 정확도를 요구한다.

이를 위해 본 논문에서는 원거리 표적인 인공위성을 활용해 지상 장거리 다기능 레이다의 출력 성능과 레이다 정렬 정확도를 검증 및 분석하는 방안을 기술한다. 위성의 사용은 국내 산악 지형 환경을 고려할 시, 원거리 표적 시험을 위한 충분한 가시거리와 균일한 지상 클러터를 찾기 어려운 환경적 제약에 좋은 대안이 될 수 있다. 따라서 궤도 및 RCS를 예측할 수 있는 인공위성의 측정을 통해 레이다의 출력 성능 및 빔 정렬을 검증하는 것은 장거리 다기능 레이다 성능 검증을 위한 효과적인 방안이 될 수 있다[6].

본 논문은 다음과 같이 구성한다. 2장에는 장거리 레이다의 출력 및 정렬 정확도를 검증하는 방안을 기술한다. 3장에서는 검증을 위한 위성을 선택하고 측정을 위한 시험 시나리오를 설명한다. 4장에서는 실제 측정값을 통해 레이다 성능을 검증하고 분석한다. 5장에서는 결론 및 토의를 기술한다.

Ⅱ. 본 론

2.1 송신출력 검증 방안

본 절에서는 장거리 레이다의 송신출력 검증 방안을 기술한다. 지상에 지정된 장소에 기준 표적을 설치해 측정하는 방법이 가장 정확한 방법이지만, 그러나 이는 별도의 장소에 표적을 일관성 있게 설치하고 보관 또는 운용해야 하는 문제가 있으며, 운용 배치 중인 레이다 장비별 별도의 표적 설치 장소를 마련하는 것은 물리적/비용적 제약이 있다.

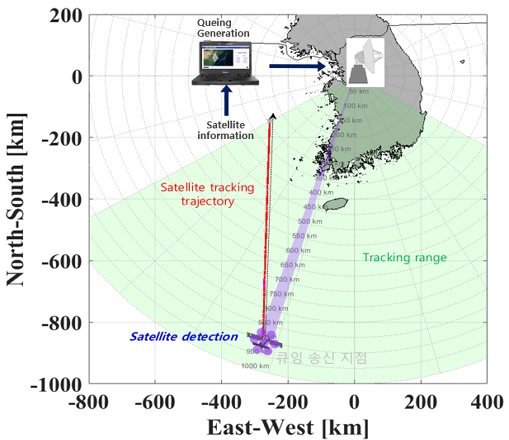
따라서 본 논문에서는 별도의 사이트에 지상 기준 표적을 설치/운용하는 방법이 아니라, 추적 및 예측을 할 수 있는 잘 알려진 위성 활용을 통해 출력 열화 등을 검증하는 방법을 기술한다. 그림 1은 위성의 사전 정보를 이용하여 위성의 예상 위치에 빔을 송신하여 포착한 후 추적을 통하여 위성으로부터 되돌아오는 수신신호를 모니터링하는 방안을 보인다[7].

Fig. 1.

Radar operation for satellite tracking

레이다를 초기에 설치 배치한 후, 또는 검/교정 후에 특정한 위성에 대한 수신전력을 측정하고, 이를 레이다 방정식을 통해 분석을 수행한다. 수신한 SNR(신호대잡음비)로부터 RCS를 구하는 과정을 식 (1)부터 식 (5)에 보인다. 여기서 α는 측정 가능한 레이다 지표를 통해 산출된다. 사용한 기호의 상세 설명은 표 1에 기술한다[8][9].

$\[ SNR=\frac{P_t{G}_t{G}_r{\lambda }^2\sigma }{{\left(4\pi \right)}^3{R}^{4}k{T}_{s}B{L}_t} \]$

(1)

$\[ \sigma =\frac{{\left(4\pi \right)}^{3}k{L}_t}{P_t{G}_t\frac{G_r}{T_s}{\lambda }^2}\frac{R^4}{\tau }SNR \]$

(2)

$\[ \sigma =\frac{{\left(4\pi \right)}^{3}k{L}_t}{EIRP\times G/T\times {\lambda }^2}\frac{R^4}{\tau }SNR \]$

(3)

$\[ \alpha =\frac{{\left(4\pi \right)}^{3}k}{EIRP\times G/T\times {\lambda }^2}\frac{1}{\tau } \]$

(4)

$\[ \sigma =\alpha \times L_t\times R^4\times SNR \]$

(5)

Table 1.

Symbol of equation (1)∼(2)

위성을 사용할 시에 큰 장점은 지상 클러터의 영향을 거의 받지 않는 점이다. 따라서 Loss 부분에 복잡한 클러터의 영향을 고려하지 않아도 된다. 레이다가 위성을 탐지하면, 거리(R) 및 SNR을 얻을 수 있고, 이를 식 (5)에 대입하면, 손실을 제외한 값들을 결정할 수 있다. 손실 L_t는 다양한 방식으로 정의되고 있으나, 본 실험에서는 다음 식 (6)과 같이 정의하여 사용한다.

$\[ L_t\left(dB\right)=L_a+L_{rsp}+L_{scan}+L_{offset} \]$

(6)

여기서, L_a는 대기 손실, L_rsp는 신호처리 손실, L_scan는 빔조향 손실, L_offset 오프셋 손실로 정의한다. 이들 값은 레이다 개발 시에 시험장치를 통해 측정 및 보정된 값이며, 맑은 날씨 환경에서 위성과 레이다 간의 빔 조향각을 계산하면, L_t를 결정할 수 있다. 따라서 기결정된 값 α 및 L_t를 식 (5)에 대입하고 레이다 측정치 거리(R)과 SNR로부터 위성의 RCS를 산출할 수 있다.

2.2 정렬 정확도 분석 및 보정 방안

2.2.1 위성 궤도 데이터

본 절에서는 위성을 이용하여 레이다의 정렬 정확도를 검증하기 위해서는 잘 알려진 위성의 정보를 활용해야 한다. 위성의 정보는 일반적으로 3가지 형태가 있다.

첫 번째 형태는 TLE(Two-Line Element, 예측 데이터)이다. TLE 데이터는 위성 위치, 속도 예측을 위한 2줄 형태 파라미터로 제공되며, 대부분 위성에 대해 제공한다[10]. 북미 항공우주 방위사령부(NOARD,　North American Aerospace Command)에서 관리 및 제공하고, 과거 위성 궤적을 활용하여, SGP4 알고리듬을 통해 예측한다. 데이터 갱신 주기(1일 2∼3회)가 길어, 시간에 따른 예측 정확도가 떨어진다. TLE 데이터의 오차범위는 본 논문에서 아용한 레이다의 오차범위보다 커서 정렬정확도 분석을 위한 정답지로 사용하기에 부적합하다. 하지만 매우 정확한 정렬 정확도를 요구하지 않는 레이다의 경우 TLE 데이터를 사용하여 검증할 수 있다.

두 번째는 CPF(Consolidated Prediction File, 예측 데이터)이다. CPF 데이터는 시간별 위성 위치 속도 예측값이며, NASA 데이터 센터(CDDIS, Crustal Dynamic Data Information System)에서 관리 및 제공하고, 국제 레이저 거리 측정 서비스(ILRS, International Laser Ranging Service)에서 위성 궤적 고정밀 예측에 사용되며, 반사경이 부착된 위성만 제공된다[11]. CPF 데이터는 위성 거리 측정(SLR, Satellite Laser Ranging) 고정밀 관측 지원에 활용되고, 통합 생성 모델(지구 중력장, 태양복사 모델 등)을 통해 예측된다. 특정 시간(수분) 간격으로 생성, 시간에 따른 예측 정확도가 매우 높다.

마지막으로 SP3(Standard Product 3, 관측 데이터)이다. SP3 데이터는 GPS 및 GNSS 위성 좌표계와 시간 정보 형태로 제공되며, CDDIS 에서 관리 및 제공한다[12]. 위성에서 수신된 신호 데이터를 사용하여 정밀궤도 계산 및 오차 보정 데이터 산출에 이용되며 데이터는 수십 초 간격으로 생성된다. 표 2는 잘 알려진 위성에 대한 RCS, 고도, 데이터 제공 형태를 보인다.

Table 2.

Characteristics of satellite and Provided data

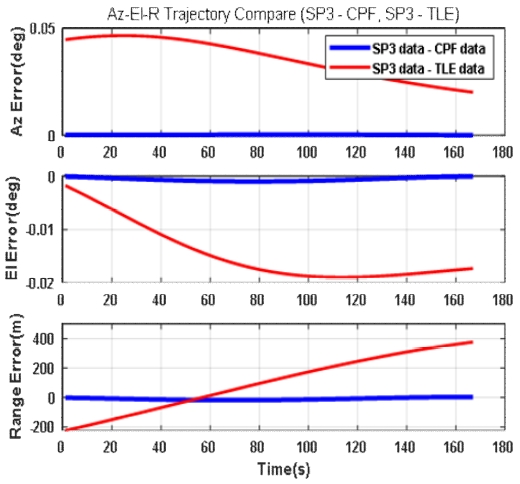
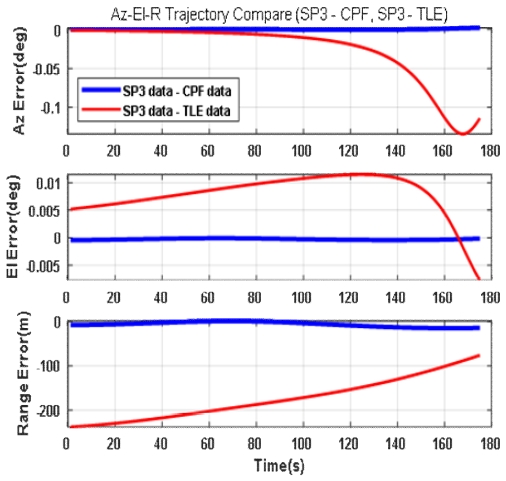
레이다의 정렬 정확도를 검증하기 위해서는 위성정보의 정확도가 중요하다. 표 2에서 언급한 위성 중 가장 정밀한 데이터를 제공하는 LARETS와 STARLETTE 위성의 TLE, CPF, SP3 데이터의 신뢰도를 그림 2와 그림 3에 같이 비교하였다.

Fig. 2.

Difference between SP3 and CPF,TLE of LARETS satellite

Fig. 3.

Difference between SP3 and CPF,TLE of STARLETTE satellite

그림 2와 그림 3은 ‘24.11.06 일자 LARETS 및 STARLETTE 위성의 데이터를 비교한 것이다. 실제 위성의 궤적 데이터와 고정밀 예측궤적(CPF), 일반예측 궤적(TLE)를 RMSE(Root mean square error)로 비교해보면 그림 2에서 볼 수 있듯이 LARETS 위성의 실제 궤적(SP3)과 고정밀 예측궤적(CPF) 데이터의 차이는 방위각 (0.0002°), 고각 (0.0007°), 거리(11.4m)로 차이가 거의 없었고. CPF와 TLE 데이터의 차이는 방위각 (0.037°), 고각 (0.015°), 거리(209.24m)로 상대적으로 차이가 큼을 확인할 수 있다.

그림 3에서 STARLETTE 위성의 차이를 비교해보면 실제 궤적(SP3)과 고정밀 예측궤적(CPF) 데이터의 차이는 방위각 (0.0005°), 고각 (0.0003°), 거리 (8.16m)이고. CPF와 TLE 데이터의 차이는 방위각 (0.05°), 고각 (0.009°), 거리 (177.1m)로 위 LARETS 위성의 차이 특성과 유사하였다.

2.2.2 레이다 추적 정렬 정확도 분석

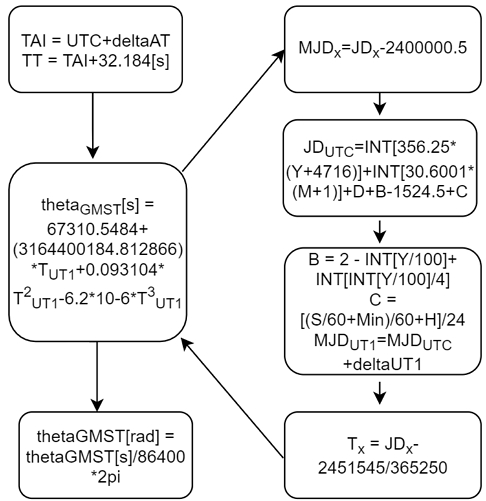
레이다 추적데이터와 위성에서 제공하는 데이터를 비교하기 위해서는 우선 좌표계를 일치시켜야 한다. 위성에서 제공하는 데이터는 TEME(True Equator, Mean Equinox) 좌표계로 표현되고, 이를 사용하기 위해서는 ECEF(Earth Centered Earth Fixed) 좌표계로 변환해야 한다[13]. 좌표계 변환을 위해서 기준(현재) 시간 정보가 반영되어야 하는데 기준 시간 정보는 그림 4와 같이 구할 수 있다.

Fig. 4.

Flow chart of time transformation

그림 4의 플로우 차트에서 TAI(international Atomic time)은 국제원자시이고, UTC(coordinated Universal teim)은 협정 세계시로 세계표준시이다[14]. ΔAT는 EOP(Earth Orientation Parameters)에서 제공되는 값 중의 하나이며, TT(Terrestrial Time)은 상대론적 효과를 반영한 이론적 시간이다. 좌표변환을 위해서는 최종적으로 θ_GMST을 구해야 한다. GMST(Greenwich Mean Sidereal Time)는 춘분점 기준으로 그리니치 자오선이 회전한 각도로 시간을 측정한다. θ_GMST을 구하기 위한 변수인 TUT 값은 차트 오른편에 도시된 방법을 통하여 구할 수 있다.

차트 오른쪽에서 MJD는 Modified Julian Date의 약자이고 JD는 Julian Date의 약자이다. 이들 약자 아래 첨자 X는 사용된 기준 시간 (UTC, UT1 등)을 나타낸다. 또한 UTC 시간은 Year(Y), Month(M), Day (D), Hour(H), Minute(Min), Sec(S)와 같고, ΔUT1는 ΔAT와 같이 EOP (Earth Orientation Parameters)에서 제공되는 값이다[15].

위에서 구한 시간 정보를 바탕으로 TEME 좌표계에서 ECEF 좌표계로 변환과정은 식 (7) ~ 식 (9)와 같다.

$\[ {\mathbf{p}}_{\mathrm{E}\mathrm{C}\mathrm{E}\mathrm{F}}=\left[\mathbf{W}\left(t,x_p,y_p\right)\right]\cdot \left[\mathbf{R}\left(t,{\theta }_{GMST}\right)\right]\cdot {\mathbf{p}}_{\mathrm{T}\mathrm{E}\mathrm{M}\mathrm{E}} \]$

(7)

$\[ \begin{array}{c}\left[\mathbf{W}\left(t,x_p,y_p\right)\right]=\hfill \\ \left(\begin{array}{ccc}\text{cos} \left(x_p\right)& \text{sin} \left(x_p\right)\text{sin} \left(y_p\right)& \text{sin} \left(x_p\right)\text{cos} \left(y_p\right)\\ 0& \text{cos} \left(y_p\right)& -\text{sin} \left(y_p\right)\\ -\text{sin} \left(x_p\right)& \text{cos} \left(x_p\right)\text{sin} \left(y_p\right)& \text{cos} \left(x_p\right)\text{cos} \left(y_p\right)\end{array}\right)\\ =\left(\begin{array}{ccc}\text{cos} \left(x_p\right)& 0& \text{sin} \left(x_p\right)\\ 0& 1& 0\\ -\text{sin} \left(x_p\right)& 0& \text{cos} \left(x_p\right)\end{array}\right)\cdot \left(\begin{array}{ccc}1& 0& 0\\ 0& \text{cos} \left(y_p\right)& -\text{sin} \left(y_p\right)\\ 0& \text{sin} \left(y_p\right)& \text{cos} \left(y_p\right)\end{array}\right)\hfill \end{array} \]$

(8)

$\[ \left[\mathbf{R}\left(t,{\theta }_{GMST}\right)\right]=\left(\begin{array}{ccc}\text{cos} \left({\theta }_{GMST}\right)& \text{sin} \left({\theta }_{GMST}\right)& 0\\ -\text{sin} \left({\theta }_{GMST}\right)& \text{cos} \left({\theta }_{GMST}\right)& 0\\ 0& 0& 1\end{array}\right) \]$

(9)

위 식 (7)에서 p_ECEF, p_TEM는 위치 벡터이고, 식 (8)에서 [W(t,x_p,y_p)]는 극이동에 대한 좌표변환 행렬, 마지막으로 식 (9)에서 [R(t,θ_GMST)] 는 항성시에 대한 좌표변환 행렬을 나타낸다.

좌표계 및 시각이 일치화된 값을 이용하여 정렬 정확도를 구간에 대한 거리, 방위각, 고각의 차이를 다음 식 (10) ~ 식 (12)를 통해 같이 계산할 수 있으며, 값들을 통해 통계적 지표(구간평균, 표준편차 등)를 산출할 수 있다.

$\[ {\text{R}}_{\text{diff}}={\text{R}}_{\text{radar}}-{\text{R}}_{\text{satellite}} \]$

(10)

$\[ \text{A}{\text{Z}}_{\text{diff}}=\text{A}{\text{Z}}_{\text{radar}}-\text{A}{\text{Z}}_{\text{satellite}} \]$

(11)

$\[ {\text{El}}_{\text{diff}}=\text{E}{\text{1}}_{\text{radar}}-{\text{El}}_{\text{satellite}} \]$

(12)

이렇게 측정된 값의 RMSE를 계산하면, 이는 레이다의 자세 틀어짐과 관련된 수치를 얻을 수 있다. 레이다 자세 틀어짐의 정도는 Heading, Roll, Pitch 값으로 파악할 수 있으며, Heading은 방위각과 관련된 자세, Pitch는 고각과 관련된 자세, Roll은 플랫폼의 뒤틀림으로 이해할 수 있다. 이 틀어진 정도를 보상함으로써, 레이다의 미세한 틀어짐을 보정한다. 레이다의 자세 틀어짐은 기구적 요인과 전기적 요인에 의해 발생한다. 기구적 오차는 레이다 자세를 측정하는 센서의 장착 오차와 관련한다. 전기적 오차는 자세 센서의 정확도, 레이다 빔 편향, 외부 환경적 요인에 의해서 발생한다. 본 레이다 장비는 INS(Inertial Navigation System)를 사용하였으며, 방위각 정확도는 0.1° 이하이다.

Ⅲ. 검증용 위성 및 시험 시나리오

3.2 시험 시나리오

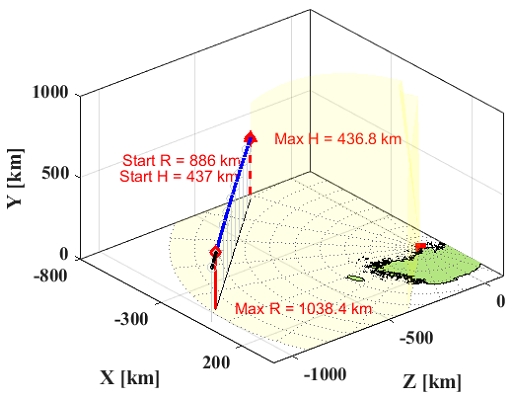
그림 5는 송신출력 검증을 위한 위성 추적 시험 중 ‘24.11.25(월)’에 수행한 ISS를 추적한 시험 시나리오를 보인다.

Fig. 5.

Radar tracking result of ISS(Zayra) satellite

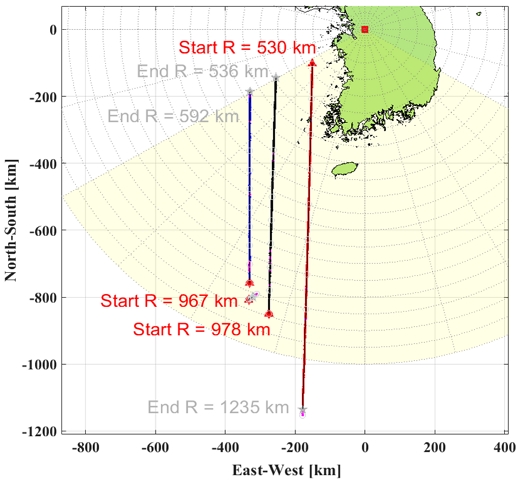
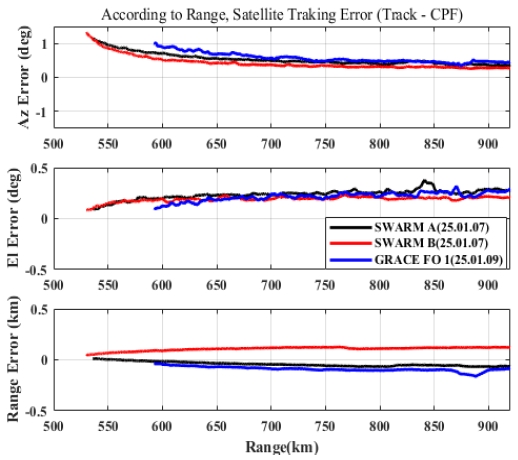
그림 6은 레이더 정렬 검증을 위한 시험 중, 한반도 서남해 방향으로 지나가는 위성을 추적한 시험 시나리오의 결과이다.

Fig. 6.

Satellite tracking result of southwestern sea direction

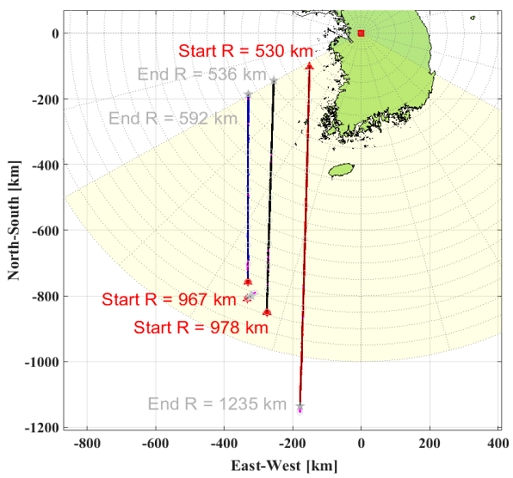
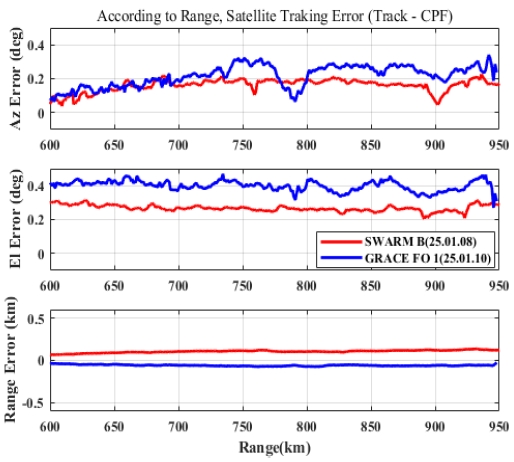
그림 7은 레이더 정렬 검증을 위한 시험 중, 한반도 남동해 방향으로 지나가는 위성을 추적한 시험 시나리오의 결과이다.

Fig. 7.

Satellite tracking result of southeastern sea direction

Ⅳ. 측정 및 분석

4.1 송신 출력 측정 및 분석

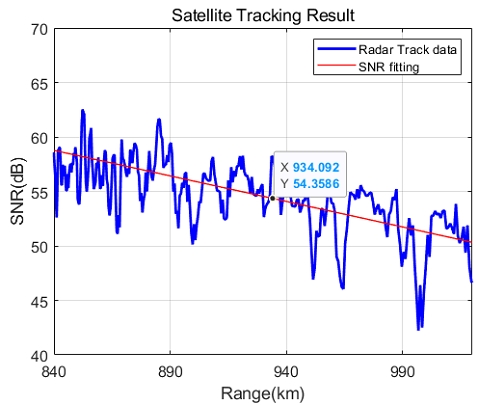
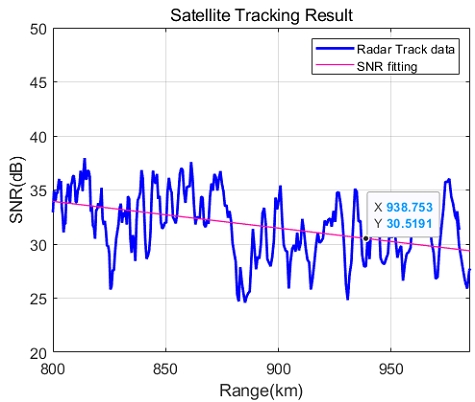
3.2절에서 그림 5에서 보인 우주정거장(ISS)의 시험 측정 결과를 그림 8 및 그림 9에 보인다. 그림 8은 정상 출력에 대한 수치를 보여주며, 그림 9는 출력 저하를 측정하기 위해 일부 반도체 송수신기 모듈의 송신을 중지한(Off) 상태에서 측정한 결과이다.

Fig. 8.

ISS SNR test – Normal operation

Fig. 9.

ISS SNR test – Output power degradation

앞의 2.1절에서 설명한 바와 식 (5)에 기결정된 값 α 및 L_t를 대입하고 그림 8 및 그림 9에서 얻은 레이다 측정치 거리(R)와 SNR를 대입하면 위성의 RCS를 산출할 수 있다. 본 논문에 활용된 레이다는 군사용으로 개발된 레이다로 보안을 위해 직접적인 수치를 계산하지 않는다. 따라서 초기 배치된 이후에 정기적으로 동일 위성에 대한 RCS 값 변화를 측정 및 살펴봄으로써 장비 출력 성능의 열화 정도를 점검할 수 있다.

4.2 정렬 정확도 측정 및 분석

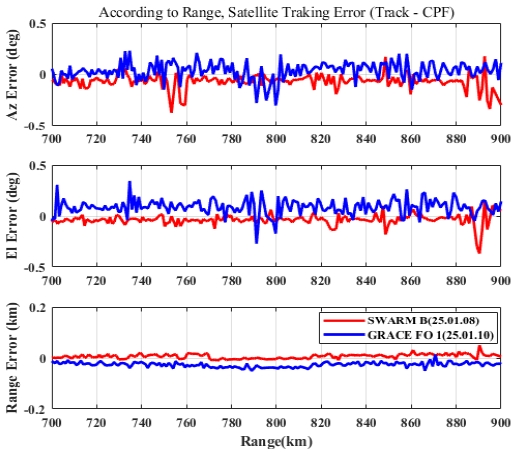
그림 6에서 보인 시나리오에 대한 정렬 정확도 측정 결과를 그림 10에 보이고, 그림 7에서 보인 시나리오에 대한 측정 결과를 그림 11에 보인다.

Fig. 10.

Accuracy measurement results of satellite alignment in the southwestern direction

Fig. 11.

Accuracy measurement results of satellite alignment in the southeastern direction

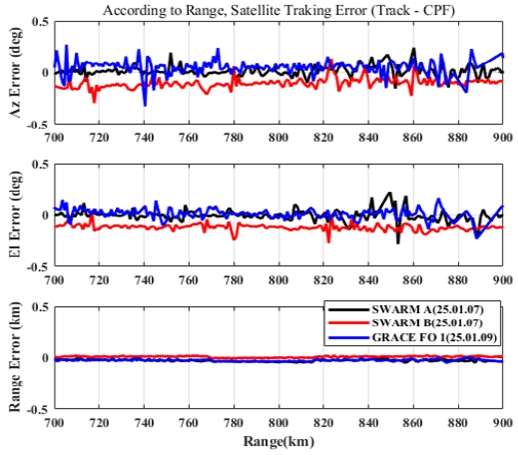
빔의 방사 각도가 양옆의 엣지(Edge)로 갈수록 빔 편향 오차가 크므로, 그림 10 및 그림 11에서 빔의 방사 각을 ±45° 이내의 데이터를 바탕으로 보상 오차 값을 산출한다. 3개의 위성의 데이터를 통합하여 보상하기 위해 개별 위성 측정 거리 및 빔 편향 오차를 고려하여 700km ~ 900km 구간의 데이터만 이용하여 보상 값을 구한다.

보상해야 할 정렬의 틀어짐은 서남해 방향 Heading -0.31367, Roll -0.39033, Pitch –0.25867, 거리 +40m로 추정하였고, 동남해 방향 Heading -0.2765, Roll -0.211, Pitch –0.2995, 거리 +40m로 추정하였다. 이를 반영하여, 레이다의 틀어짐을 추가 보상한 결과를 그림 12 및 그림 13에 보인다. 방향/위성별 틀어짐과 보상 전/후의 정확도 값은 표 3과 같다. 표 3에서 위의 값은 위성별 틀어짐의 정도이고, 아래 값은 추정된 보상 값을 적용한 후 틀어짐의 정도를 나타낸 값이다.

Fig. 12.

Calibration results of satellite alignment in the southwestern direction

Fig. 13.

Calibration results of satellite alignment in the southeastern direction

Table 3.

Calibration results of satellite/direction-based alignment

Ⅴ. 결 론

본 논문에서는 군사용으로 개발된 지상 장거리 레이다의 출력 및 정렬을 검증하기 위해 위성을 활용하는 방법을 제시하고 시험을 진행하였다. 출력 검증은 RCS가 알려진 인공위성 추적을 통해 얻은 값을 주기적으로 모니터링함으로써 출력의 열화를 검증하는 방법을 제시 및 측정하였다. 측정 결과 동일 위성에 대해 출력이 일관성이 있게 유지됨을 확인하였고, 송신출력이 떨어지게 되면 결과치 역시 감소함을 확인하였다. 레이다의 정렬은 검증을 위해 가용한 위성을 선별하고, 다수의 시험을 통해 위성 추적시험을 통하여, 레이다 자세의 틀어짐을 확인하였다. 이 틀어짐을 추가 보상함으로써 더욱더 정확한 레이다 자세를 보정 하였다.

위성을 활용해 레이다 성능을 검증하는 방법은 장비의 유지 보수 측면에서 효과적인 대안이 될 수 있다. 향후 이 방법을 적용하기 위해서는 다음 사안이 추가로 논의 및 연구되어야 한다. 장비 운용을 중단하고 검/교정 수리를 진행하기 위한 출력 저하 및 자세 틀어짐에 대한 기준을 정해야 한다. 또한 자세 틀어짐과 관련하여, 더 정밀한 자세 측정장치를 레이다 장비에 탑재하고, 많은 수의 위성 측정 시험을 통해 확보한 통계적 지표를 바탕으로 레이다 자세를 정밀하게 보정 하는 추가 연구가 필요하다.

References

• T. Kinghorn, I. Scott, and E. Totten, "Recent advances in airborne phased array radar systems", Published in: 2016 IEEE International Symposium on Phased Array Systems and Technology (PAST), Waltham, MA, USA, pp. 18-21, Oct. 2016. [https://doi.org/10.1109/ARRAY.2016.7832541]
• Y. Mancuso, P. Gremillet, and P. Lacomme, "T/R- Modules Technological and Technical Trends for Phased Array Antennas", 2005 European Microwave Conference, Paris, France, pp. 11-16, Oct. 2005. [https://doi.org/10.1109/EUMC.2005.1610051]
• A. Agrawal and A. Jablon "A calibration technique for active phased array antennas", 2003 IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, pp. 14-17, Oct. 2003. [https://doi.org/10.1109/PAST.2003.1256985]
• C. Fulton, J. L. Salazar, Y. Zhang, G. Zhang, R. Kelly, and J. Meie, "Cylindrical polarimetric phased array radar: Beamforming and calibration for weather applications", IEEE Transactions on Geoscience and Remote Sensing, Vol. 55, No. 5, pp. 2827-2841, May 2017. [https://doi.org/10.1109/TGRS.2017.2655023]
• D. Cataldo, L. Gentile, S. Ghio, E. Giusti, S. Tomei, and M. Martorella, "Multibistatic Radar for Space Surveillance and Tracking", IEEE Aerospace and Electronic Systems Magazine, Vol. 35, No. 8, pp. 14-30, Aug. 2020. [https://doi.org/10.1109/MAES.2020.2978955]
• M. L. Stone and G. P. Banner, "Radars for the Detection and Tracking of Ballistic Missiles, Satellites, and Planets", Lincoln Laboratory Journal, Vol. 12, No. 2, Jan. 2000.
• J. Kim and S. Hong, "Satellite tracking method using ground-based multi function radar", Summer conference, KIEES, Pyeongchang, Korea, Aug. 2024.
• B. R. Mahafza, "Radar Systems Analysis and Design Using MATLAB", Chapman & Hall/CRC, pp. 21-40, Apr. 2005. [https://doi.org/10.1201/9781420057072]
• J. Kwon, J. Kim, and S. Hong, "Experimental test of Long Range Radar RCS calibration and measurement", Summer conference, KIEES, Pyeongchang, Korea, Aug. 2024.
• https://www.space-track.org/#g, . [accessed: Jan. 17, 2025]
• https://cddis.nasa.gov/archive/slr/cpf_predicts_v2/2024, . [accessed: Jan. 17, 2025]
• https://cddis.nasa.gov/archive/slr/products/orbits, . [accessed: Jan. 17, 2025]
• B. Hofmann-Wellenhof, H. Lichtenegger and J. collins, "Grobal Positioning System : Theory and Practice", sigmapress, pp. 33-49, 2009.
• D. D. McCarthy, "The Definition of UTC", International Astronomical Union Colloquium, Towards Models and Constants for Sub –Microarcsecond Astrometry, Vol. 180, pp. 363-371, Mar. 2000. [https://doi.org/10.1017/S0252921100000506]
• M. Kalarus, et al., "Achievements of the Earth orientation parameters prediction comparison campaign", Journal of Geodesy, Vol. 84, pp. 587-596, Sep. 2010. [https://doi.org/10.1007/s00190-010-0387-1]