해면골 비율이 저강도 집속 초음파에 미치는 영향 분석: 시뮬레이션 연구

Ⅰ. 서 론

뇌 신경조절(Neuromodulation) 기법은 전기 또는 자기 자극을 뇌 특정 부위에 전달하여 신경 세포의 활성 정도를 조절하는 기술이다. 비침습적 방법 중 경두개 전기 자극 기법과 경두개 자기 자극 기법은 두개골 절개 없이 적용할 수 있어 정신의학 분야에서 주목받고 있다[1]. 그러나 기존의 전기 자극 기법은 공간 해상도가 낮아, 일반적으로 뇌의 표면에 한정된 넓은 뇌 영역을 자극하게 되어 국소 부위 자극에 한계가 있다[2]. 반면 집속 초음파를 이용한 신경조절 기법은 높은 공간 해상도를 제공하며[3], 고강도 집속 초음파는 조직 절제술, 저강도 집속 초음파(LIFUS, Low-Intensity Focused UltraSound)는 신경조절과 뇌혈관장벽을 개통 후 약물 전달 기술로 사용된다[4]. LIFUS는 임상 연구에서 안전성이 입증되어 활발히 연구되고 있다[5].

LIFUS를 활용할 때 목표 부위에 원하는 양의 초음파 에너지를 전달하는 것이 중요하다. 하지만 두개골의 기하학적 구조는 나이, 성별 등에 따라 다양하며 두개골 내의 불균일성으로 인해 초음파의 반사, 굴절 및 감쇠 현상이 발생해서 원하는 결과를 얻기 어렵다[2]. 이러한 이유로 목표 영역이 아닌 다른 뇌 조직에 에너지가 전달되는 현상이 발생할 수 있다.

두개골에 의한 초음파 에너지 감쇠 정도와 초점 영역을 추정하기 위해 의료 영상을 활용한 시뮬레이션 과정을 통해 예측할 수 있다[6]. 컴퓨터단층촬영(CT, Computed Tomograph) 이미지는 두개골의 외벽을 형성하는 단단한 치밀골(Compact bone)과 빈 공간이 존재하는 해면골(Cancellous bone)로 이루어진 구조에 대한 불균질한 물성 정보를 제공한다. 따라서, 정확한 두개골 정보를 반영한 시뮬레이션을 위해서는 CT 영상을 활용한 접근이 필요하다. 예를 들면, Pinton 연구팀[7]은 CT 이미지를 통해 두개골 모델을 만들어 초음파의 감쇠, 산란 그리고 흡수의 영향을 정량화 결과를 발표했다. Mueller 연구팀[8]은 개개인의 두개골 구조의 차이가 초음파의 파동 전파에 미치는 영향을 평가했으며, 이때 주파수와 시뮬레이션의 선형 및 비선형 조건에 따른 차이를 관찰하였다.

그러나 CT 이미지는 방사선 노출의 위험성으로 단지 시뮬레이션 목적으로 영상을 획득해서는 안 된다[9][10]. 자기공명영상(MRI, Magnetic Resonance Imaging)은 CT 이미지보다 뇌 조직을 상세하게 분별할 수 있어 최근 MRI를 활용한 LIFUS 시뮬레이션 연구가 진행되었다[2][3][11][12]. 예를 들면, Huang 연구팀은 MRI를 통해 상세한 뇌 구조를 분별해서 인간 두개골 모델을 구현한 뒤 뇌 조직별로 물성값을 변화시키면서 경두개 집속 초음파(tFUS, transcranial Focused UltraSound) 시뮬레이션 결과를 수치적으로 분석하고 음속 물성이 tFUS에 가장 큰 영향을 미치는 요인이라고 보고했다[2]. 그리고 MRI를 통해서 타겟 부위인 감각 시상의 위치를 찾는데 사용한 연구가 있고[3], 시뮬레이션을 위해 뇌의 상세한 구조를 모델링한 연구가 있다[11].

이렇게 MRI를 사용한 LIFUS 시뮬레이션에서는 두개골에 균일한 물성을 부여하는데, 이때 두개골 전체를 단일 층으로 고려하거나 해면골 영역을 분할하여 3개의 층으로 나누어 물성을 부여하는 방식으로 진행되었다. 반면, CT의 경우 해면골 영역에 불균일한 물성을 부여한다. 이러한 차이를 알아보기 위해 최근 본 연구팀은 두 접근 방식이 초음파 전파에 미치는 영향을 비교하는 연구를 수행하였다 [1][12]. 그 결과 해면골의 물성값에 따라 두개골 통과 이후 음압 분포의 다양한 변화를 관측했으며 이를 통해 해면골을 고려한 모델링의 중요성을 확인하였다.

J. K. Mueller et al.[8]은 CT 이미지 기반의 두개골 모델을 만들어 개인별 두개골 두께에 따른 최대 음압 또는 집속 영역 부피의 상관관계를 살펴보았으나, 유의미한 선형 관계는 발견하지 못했다. 본 연구팀은 해면골의 존재가 tFUS 시뮬레이션에 중요한 요인임을 확인했지만, 그 영향은 아직 체계적으로 조사되지 않았다. 따라서, 우리는 두개골 내 해면골 비율이 미치는 영향을 분석하고자 한다. 이 과정에서 의료 영상 기반의 두개골 모델을 사용하려 했으나, 해부학적 구조가 복잡하여 해면골 비율의 영향을 집중적으로 분석하기 어려웠다. 이에 본 연구팀은 단순화된 구 모형을 제작하여 연구를 진행했다. 구 모형에서 뇌 조직을 모두 물로 대체하여 LIFUS 시뮬레이션에 영향을 미치는 모든 요인을 배제하고 두개골에서 해면골 비율만 고려하여 두개골 통과 이후 음압 분포에 미치는 영향을 분석하고자 한다.

본 논문은 다음과 같이 구성된다. 2장에서 3차원 음압 모델링 방법을 설명하고 3장에서 본 연구에서 진행한 시뮬레이션의 결과와 분석을 기술한 뒤 4장에서 결론과 추후 연구 계획을 언급한다.

Ⅱ. 연구 방법

LIFUS 시뮬레이션을 위해 3차원 음향 모델을 활용한 음압 계산이 필요하다. 이러한 계산은 MATLAB의 초음파 시뮬레이션 오픈 소스인 k-Wave MATLAB toolbox[13]를 이용해서 진행했고 이때 최대한 사람의 머리와 비슷한 곡률의 단순 구형 모델을 구현했다[14]. 트랜스듀서는 0.5MHz의 단일 요소 집속 트랜스듀서(Blatek, Inc., State College, PA)의 규격에 따라 반지름과 직경을 30mm로 모델링하고 압력을 1MPa로 설정했다. 이후 전단파의 영향을 무시하기 위해 트랜스듀서를 두개골과 수직으로 배치하고[8] 10mm 떨어진 지점에 위치시켰다. 본 연구에서 0.5MHz를 사용했기 때문에 k-Wave 계산 공간은 0.42mm3 크기의 등방성 복셀로 구성했고[15] 85mm의 반지름을 가진 두개골과 10mm의 트랜스듀서와의 거리를 모두 포함할 수 있도록 500 × 500 × 500개의 그리드로 구성된 3D 공간을 구현했고, 전체 공간의 크기는 21cm × 21cm × 21cm이다.

해면골은 IT’IS Foundation에서 제공하는 데이터 셋을 참고해서 0.5MHz 주파수에서 두개골과 물의 물성(음속, 밀도, 감쇄 계수)을 계산했다[16](표 1). 이때 두개골 내에 존재하는 뇌 조직은 tFUS 결과에 거의 영향을 주지 않기 때문에 가장 비슷한 값을 가진 물로 대체해 모델을 단순화했다[17]. 또한 실제 tFUS를 적용할 때 두피와 트랜스듀서 사이의 커플링 매체로 사용하는 물을 고려하기 위해 두개골이 물에 잠겨있다고 가정했다[18].

Table 1.

acoustic properties of water and skull

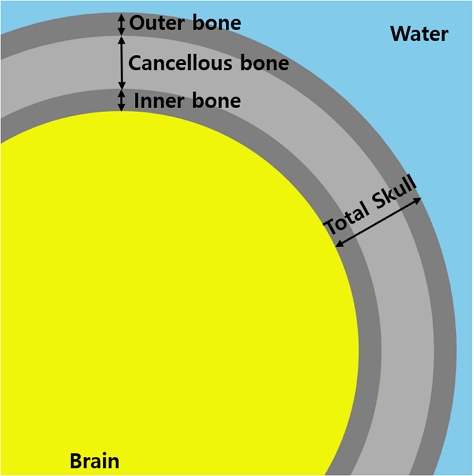
뇌 조직과 두개골을 80mm, 85mm 크기의 반지름을 가진 단순 구형 즉, 반지름 80mm의 뇌와 이를 둘러싸고 있는 5mm 두께의 두개골을 구현했다[13]. 그리고 해면골을 두개골 중심에서부터 두개골 두께의 0%부터 10% 간격으로 80%까지 증가시켜 전체 두개골(inner, cancellous, outer)을 3layer로 모델링하고 3D 시뮬레이션을 진행했다(그림 1).

Fig. 1.

simple sphere model simulation setting

이후 다양한 두개골 두께에 대해서 해면골의 영향을 확인하기 위해 5mm 외의 두개골 두께를 추가로 모델링했다. 이때 트랜스듀서와 두개골의 곡률 차이가 초음파 입사각에 미치는 영향을 배제하기 위해 뇌 조직을 1mm 줄이는 동시에 두개골을 1mm 씩 증가시켜 두개골 모델의 반지름(85mm)을 고정시킨 상태에서 두개골 두께를 5mm에서 8mm까지 늘려가는 방법으로 3D 시뮬레이션을 추가로 진행했다. 따라서 총 36가지 경우(= 두개골 두께 5, 6, 7, 8 mm × 해면골 비율 0~80%, 10% 간격으로 총 9가지 경우)에 대해서 시뮬레이션을 진행했다.

결과는 최대 압력과 집속 영역 부피(FWHM, Full Width at Half Maximum)로 분석되었다. 이때 집속 영역 부피는 각 모델에서 최대 음압의 절반에 해당하는 지점에서 부피를 측정하는 방법으로 일반적으로 최대 음압의 절반을 기준으로 하지만 용이한 결과 분석을 위해 이 지점을 바꾸기도 한다[19]. 집속 영역 부피를 최대 음압의 절반을 기준으로 측정하게 되면 모델마다 기준이 달라지기 때문에 본 연구팀은 36가지 모델 중 가장 낮은 최대 음압을 보인 두개골 두께가 8mm고 해면골 비율이 40%인 경우에 관찰되는 최대 음압을 기준으로 집속 영역 부피를 측정했다. 이러한 방법을 집속 영역 부피(min, FWHMmin)라고 지칭한다.

Ⅲ. 연구 결과 및 분석

본 연구는 두개골 내에 존재하는 해면골의 비율이 LIFUS 시뮬레이션 결과에 미치는 영향을 확인하기 위해 해면골 비율을 10%씩 변화시키며 최대 음압과 집속 영역을 분석하였다. 추가로 두개골의 영향을 확인하기 위해 동일 조건이면서 두개골이 없는 자유수에서 시뮬레이션을 추가로 진행하였다. 이때 최대 음압과 집속 영역 부피는 각각 8.1899MPa, 211.89mm3였다. 이후 자유수 대비 두개골 모델에서 결과를 비교하기 위해 음압비(두개골 모델에서 최대 비율을 사용해서 결과를 분석했다.

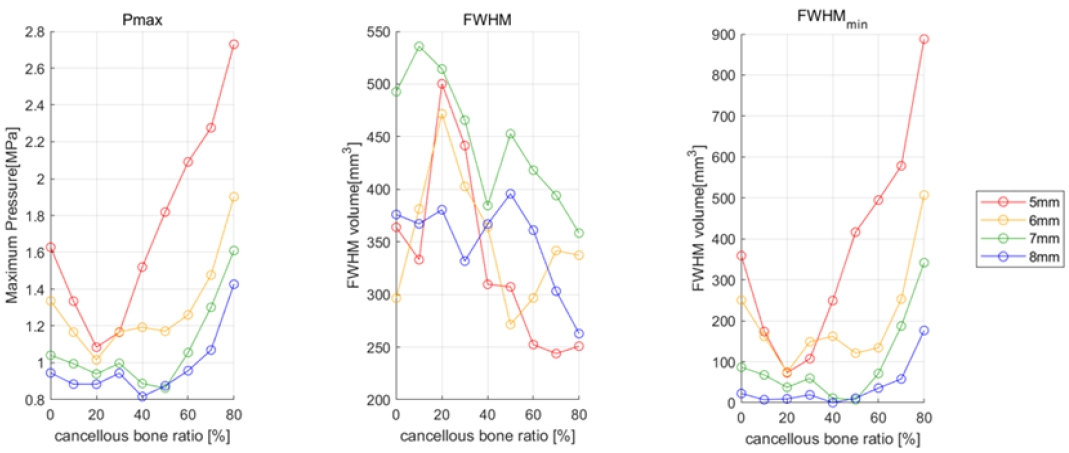
전체 시뮬레이션 결과는 그림 2와 같다. 전반적으로 두개골 두께가 두꺼울수록 최대 음압은 감소하며 이는 기존의 연구 결과들과 동일하다[8][20]. 또한 모든 두개골 두께에 대해서 해면골 비율이 증가함에 따라 최대 음압은 감소하다가 특정 비율에서 다시 증가하는 경향을 보인다. 이는 물과 두개골 간의 물성 차이로 인한 초음파 반사, 굴절 및 감쇠 현상이 치밀골과 그 내부에 있는 해면골 사이에서도 일어나기 때문으로 예상된다[21]. 이러한 최대 음압의 경향이 변하는 지점 즉, 가장 낮은 최대 음압을 보이는 해면골 비율은 두개골 두께가 5, 6, 7, 8mm면 20, 20, 50, 40%일 때 관찰되며 가장 높은 최대 음압은 두개골 두께와 상관없이 모두 80%에서 관찰된다. 다시 말해 두개골 두께가 5, 6mm일 때 해면골 비율이 작을 때는 최대 음압이 감소하고 30%를 기준으로 다시 증가한다. 7, 8mm일 때도 동일하게 감소하다가 30%에서 증가하는데 40%에서 다시 감소했다가 7mm는 60%, 8mm는 50%일 때 다시 증가하는 패턴을 보인다. 또한 해면골 비율에 따라 두개골 두께의 영향이 바뀐다. 또한, 두개골에 의해 물 대비 최대 압력이 가장 적게 감소한 경우는 두개골 두께가 5mm이고 해면골 비율이 80%일 때로 33.33%까지 감소하였다. 반면, 가장 많이 감소한 경우는 두개골 두께가 8mm이고 해면골 비율이 40%인 경우로, 9.97%까지 감소하였다.

Fig. 2.

Simulation result(Max pressure, FWHM, FWHMmin)

집속 영역 부피는 해면골의 비율이 증가함에 따라 증가와 감소를 반복하는 경향을 보인다. 이는 모든 모델에 대해서 동일한 값을 기준으로 측정한 집속 영역 부피(min)가 아니라 모델마다 최대 음압의 절반을 기준으로 측정했기 때문으로 보인다. 또한, 기존 시뮬레이션 연구에서 유의미한 선형 관계는 아니지만, 두개골 두께가 증가할 때 집속 영역 부피도 증가하는 경향이 관찰되었으며[8], 본 연구에서도 두개골 두께가 5, 6mm인 경우보다 7mm인 경우에 더 큰 집속 영역 부피가 관찰된다. 그리고 해면골의 비율이 0%에서 80%로 증가할 때, 집속 영역의 부피는 두개골 두께가 6mm인 경우를 제외하고 전반적으로 감소하는 경향을 보였다. 예를 들어, 두개골 두께가 5mm인 경우에는 약 31% 감소하였고, 7mm에서는 약 27% 감소하였다. 반면, 두개골 두께가 6mm인 경우에는 집속 영역이 오히려 증가하는 특이한 경향을 나타냈다. 즉, 해면골의 비율이 커질수록 초음파가 더 좁은 영역에 집속된다는 것을 의미한다. 집속 영역 부피(min)를 분석한 결과 최대 음압과 유사한 경향이 관측되었다. 즉, 두개골 두께가 5, 6, 7, 8mm일 때 집속 영역 부피(min)는 20, 20, 50, 40%를 기준으로 전반적으로 감소하다가 다시 증가한다. 또한 집속 영역 부피는 최저 243.82mm³에서 최대 535.73mm³ 범위에서 생성되는 반면 집속 영역 부피(min)의 경우 최저 7.33mm³에서 최대 888.09mm³ 범위에서 생성되며 기존의 방법보다 더 큰 변동을 보인다.

추가로 초점 거리와 집속 영역의 장축, 단축도 같이 조사했으며 초점 거리는 두개골 두께마다 모두 일관되지 않게 다른 패턴을 보인다. 또한 두개골 두께가 5mm일 때 해면골의 비율이 60% 이상이거나, 두개골 두께가 8mm일 때 해면골 비율이 30% 이하면 초점 거리가 일정 수치에 수렴하는 현상을 관찰했다. 집속 영역의 장축이나 단축의 경우 모든 두개골 두께에 대해서 집속 영역 부피와 전반적으로 비슷한 경향을 보였으며 이는 집속 영역 부피가 집속 영역 장축과 단축에 비례하기 때문으로 예상된다.

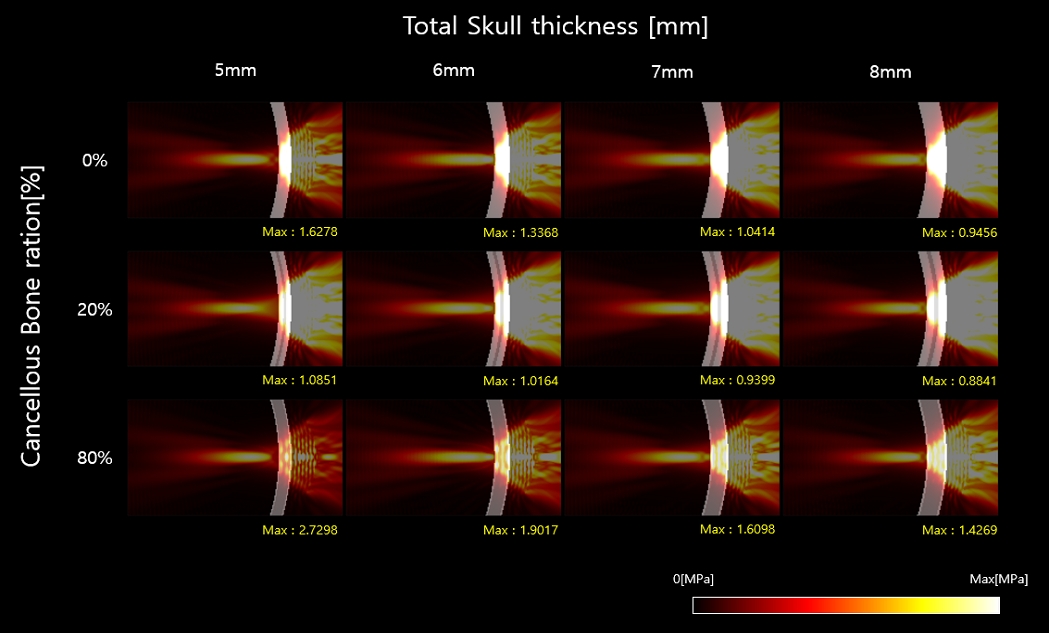
마지막으로 해면골 비율이 0, 20, 80%일 때 모든 두개골 두께에 대해 빔패턴 시각화 결과를 그림3에 나타냈다. 그림 2에 제시된 최대 음압의 패턴은 그림 3의 시각화 결과에서도 확인할 수 있다. 해면골 비율이 0%에서 20%로 증가할 때, 두개골 두께가 5mm, 6mm인 경우 최대 음압이 감소하였다(그림 3).

Fig. 3.

Beam pattern images according to cancellous bone ration(0, 20, 80%) at each skull thickness

빔 패턴 시각화 결과에서는 해면골 비율이 0%에서 20%로 증가할 때 두개골에서 반사되는 초음파의 세기가 증가하는 것을 확인할 수 있으며, 이로 인해 두개골로 전달되는 음압이 줄어든 것으로 보인다. 두개골 두께가 7mm, 8mm인 경우, 0%와 20% 해면골 비율에서 유사한 최대 음압이 관측되었으며, 빔 패턴 시각화에서도 유사한 세기의 두개골에서 반사되는 초음파 세기를 관찰할 수 있다. 일반적으로, 모든 두개골 두께에 대해 해면골 비율이 20%에서 80%로 증가하면 최대 음압이 다시 증가하여, 반사되는 초음파의 세기가 감소하는 빔 패턴을 관찰할 수 있다.

본 연구에서는 LIFUS 시뮬레이션을 통해 두개골 두께와 해면골 비율에 따른 최대 압력과 집속 영역 부피(FWHM, FWHMmin)를 분석했으며, 이에 따른 빔 패턴을 제시하였다. 최대 음압의 경우 일정 해면골 비율까지 감소하다가 이후 다시 증가하며 이때 증가하는 속도가 더 빠르다. 동일한 해면골 비율에 대해서 두개골 두께가 증가하면 최대 음압이 감소한다. 집속 영역 부피의 경우 감소와 증가를 반복하지만, 해면골 비율이 증가함에 따라 전반적으로 부피가 줄어드는 경향을 보인다. 그러나 집속 영역 부피(min)의 경우 최대 음압과 비슷한 경향을 보였으며 측정 방법에 따라 다른 경향을 관찰할 수 있었다. 마지막으로 빔 패턴의 경우 모든 두개골 두께에 대해서 해면골 비율이 0%, 20%일 때 집속 영역이 80%일 때보다 일반적으로 크다는 그림 3의 수치적 결과를 시각적으로 보여준다.

Ⅳ. 결 론

본 연구에서는 LIFUS 시뮬레이션을 통해 두개골 두께와 해면골 비율이 초음파 전달에 미치는 영향을 분석하였다. 두개골 모형을 구형으로 단순화하고 해면골의 비율을 조절함으로써, 기존의 복잡한 해부학적 구조를 고려한 모델에서 관측하지 못한 두개골과 해면골의 영향을 관찰할 수 있었다. 본 연구팀은 Mueller의 연구 결과[8]와 마찬가지로 두개골 두께에 따른 선형적인 결과를 보여주지 못했으나, 해면골의 비율이 LIFUS 결과에 중요한 영향을 미칠 수 있는 요인임을 발견하였다.

실험 결과에서 관찰한 바와 같이, 해면골의 비율에 따라 두개골 두께가 최대 음압에 미치는 영향이 달랐다. 이러한 영향을 확인하기 위해, 향후 연구에서는 치밀골과 해면골 사이에서 발생하는 초음파의 반사와 굴절 분포를 조사할 예정이다. 이를 위해 계산 공간의 해상도를 증가시켜 더 다양한 해면골 비율과 두개골 두께에 대해 시뮬레이션을 진행하여 데이터 셋을 확보한 뒤, 인공지능 모델을 학습시킬 계획이다. 이후, 이 모델을 통해 해면골 비율과 두개골 두께의 관계를 예측하고, 이를 해부학적 구조를 반영한 실제 두개골 모델에도 적용하여 해면골 비율과 두개골 두께에 따른 최대 음압을 예측하고자 한다.

Acknowledgments

본 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원(RS-2023-00280241)을 받아 수행되었습니다

References

• H. Seo and E. H. Lee, "Comparison of analysis results according to heterogeneous or homogeneous model for CT-based focused ultrasound simulation", Journal of Biomedical Engineering Research, Vol. 43, No. 6, pp. 369-374, Dec. 2022.
• Y. Huang, et al., "Numerical investigation of the energy distribution of low-intensity transcranial focused ultrasound neuromodulation for hippocampus", Ultrasonics, Vol. 124, Aug. 2022. [https://doi.org/10.1016/j.ultras.2022.106724]
• W. Legon, et al., "Neuromodulation with single‐element transcranial focused ultrasound in human thalamus", Human brain mapping, Vol. 39, No. 5, pp. 1995-2006, May 2018. [https://doi.org/10.1002/hbm.23981]
• H. Seo, W. H. Choi, and E. H. Lee, "A study of cavitation simulation by focused ultrasound stimulation", Journal of KIIT, Vol. 20, No. 12, pp. 141-148, Dec. 2022. [https://doi.org/10.14801/jkiit.2022.20.12.141]
• W. Legon, et al., "Transcranial focused ultrasound modulates the activity of primary somatosensory cortex in humans", Nature neuroscience, Vol. 17, No. 2, pp. 322-329, Jan. 2014. [https://doi.org/10.1038/nn.3620]
• S. Guo, et al., "Feasibility of ultrashort echo time images using full-wave acoustic and thermal modeling for transcranial MRI-guided focused ultrasound (tcMRgFUS) planning", Physics in Medicine & Biology, Vol. 64, No 9, Apr. 2019. [https://doi.org/10.1088/1361-6560/ab12f7]
• G. Pinton, et al., "Attenuation, scattering, and absorption of ultrasound in the skull bone", Medical physics, Vol. 39, No. 1, pp. 299-307, Dec. 2011. [https://doi.org/10.1118/1.3668316]
• J. K. Mueller, et al., "Numerical evaluation of the skull for human neuromodulation with transcranial focused ultrasound", Journal of neural engineering, Vol. 14, No. 6, Nov. 2017. [https://doi.org/10.1088/1741-2552/aa843e]
• V. M. Restrepo, et al., "Influence of skull modeling approaches on EEG source localization", Brain topography, Vol. 27, pp. 95-111, Sep. 2014. [https://doi.org/10.1007/s10548-013-0313-y]
• G. Huiskamp, et al., "The need for correct realistic geometry in the inverse EEG problem", IEEE Transactions on Biomedical Engineering, Vol. 46, No. 11, pp. 1281-1287, Nov. 1999. [https://doi.org/10.1109/10.797987]
• A. Abdolhosseinzadeh, A. Mojra, and A. Ashrafizadeh, "A numerical study on thermal ablation of brain tumor with intraoperative focused ultrasound", Journal of thermal biology, Vol. 83, pp. 119-133, Jul. 2019. [https://doi.org/10.1016/j.jtherbio.2019.05.019]
• H. Seo, et al., "Numerical Investigation of Layered Homogeneous Skull Model for Simulations of Transcranial Focused Ultrasound", Neuromodulation : Technology at the Neural Interface, Apr. 2024. [https://doi.org/10.1016/j.neurom.2024.04.001]
• B. T. Cox, et al., "K-space propagation models for acoustically heterogeneous media: application to biomedical photoacoustics", The Journal of the Acoustical Society of America, Vol. 121, No. 6, pp. 3453-3464, Jun. 2007. [https://doi.org/10.1121/1.2717409]
• P. C. Miranda, M. Lomarev, and M. Hallett, "Modeling the current distribution during transcranial direct current stimulation", Clinical Neurophysiology, Vol. 117, No. 7, pp. 1623-1629, Jul. 2006. [https://doi.org/10.1016/j.clinph.2006.04.009]
• J. H. Yu, et al., "A simulation study of Low-Intensity Focused Ultrasound Simulation According to Diameter of Transducer", Journal of KIIT, Vol. 22, No. 7, pp. 153-160, Jul. 2024. [https://doi.org/10.14801/jkiit.2024.22.7.153]
• https://itis.swiss/who-we-are/.2024, [accessed: Dec. 08, 2024]
• J. K. Mueller, et al., "Computational exploration of wave propagation and heating from transcranial focused ultrasound for neuromodulation", Journal of neural engineering, Vol. 13, No. 5, Jul. 2016. [https://doi.org/10.1088/1741-2560/13/5/056002]
• G. Darmani, et al., "Non-invasive transcranial ultrasound stimulation for neuromodulation", Clinical Neurophysiology, Vol. 135, pp. 51-73, Mar. 2022. [https://doi.org/10.1016/j.clinph.2021.12.010]
• T. Y. Park, et al., "Real-time acoustic simulation framework for tFUS: a feasibility study using navigation system", Neuroimage, Vol. 282, Nov. 2023. [https://doi.org/10.1016/j.neuroimage.2023.120411]
• J. Guo, et al., "Mathematical Model of Ultrasound Attenuation With Skull Thickness for Transcranial-Focused Ultrasound", Frontiers in Neuroscience, Feb. 2022. [https://doi.org/10.3389/fnins.2021.778616]
• M. Chen, et al., "Numerical and experimental evaluation of low-intensity transcanial focused ultrasound wave propagation using human skulls for brain neuromodulation", Medical physics, Vol. 50, No. 1, pp. 38-49, Nov. 2022. [https://doi.org/10.1002/mp.16090]