이미지 센서 생산량 최대화를 위한 재공 소진 시스템 설계
초록
4차 산업혁명이 가속화됨에 따라 자율주행 자동차, 스마트 폰의 이미지 센서 등에 사용되는 고성능 반도체 제품의 수요도 증가하고 있다. 특히 다변화되는 고객 수요에 대응하기 위해 라인 내 재공을 우선적으로 소진하여 고객 납기를 충족하고, 재공 부족에 따른 생산량 감소 문제를 해결하기 위해 투입량을 결정하는 생산 관리 방식의 중요성이 부각되고 있다. 이에 본 논문에서는 이미지 센서의 제조 특성이 반영된 생산량 최대화 최적화 모델을 수립하고 도출된 생산량을 만족시키기 위한 재공 우선 소진 기반의 생산량 투입 결정 시스템을 개발하여 제안하였다. 본 연구는 실제 반도체 생산 라인을 기반으로 모델링 하였으며, FIXED, CONWIP, Target in Rule 투입 규칙 기반의 다양한 데이터 세트를 기반으로 성능 평가를 수행하였다. 제안된 생산량 투입 결정 시스템을 통해 다른 투입 규칙 대비 18.8% 이상 생산량을 높일 수 있는 결과를 도출해 내었다.
Abstract
The demand for high-performance semiconductor products used in autonomous vehicles, smartphone image sensors, and other applications is increasing. In particular, to respond to the diversifying customer demands, it is crucial to prioritize the depletion of Work-In-Progress(WIP) to meet due date and production volume reduction issues caused by WIP shortages. In this paper, we proposed an optimization model for maximizing production that reflects the manufacturing characteristics of image sensors. Additionally, we developed a production input system based on WIP prioritization to meet the derived production targets. The performance evaluations were conducted using diverse datasets based on input rules such as FIXED, CONWIP, and Target-in-Rule. As a result of experiment, the proposed production input decision system can increase production output by more than 18.8% compared to other input rules.
Keywords:
input rule, work-in-process, image sensor, schedulingⅠ. 서 론
4차 산업혁명이 가속화됨에 따라 반도체 칩의 수요도 급격하게 증가하고 있다. 자율주행 자동차를 위한 AI(Artificial intelligence) 기반 고성능 반도체부터 모바일 디바이스에 탑재되는 이미지 센서(Image sensor) 칩을 포함하여 고객의 수요가 급증하고 있다[1]. 특히 기존 디지털 카메라의 수요량 감소와 스마트폰으로의 카메라 사용 패턴 전환도 이미지 센서의 수요량 증가를 견인하고 있다.
고성능 칩에 대한 필요성과 고객 다변화로 인한 공정의 복잡화 등에 대응하여 제품의 다양한 제조 특성이 반영된 혼합생산 전략을 수립하고 적용하는 것이 글로벌 생산 트렌드 변화에 더욱 부합하게 되었다. 특히 이미지 센서 분야에서는 재공 부족에 따른 생산량 감소 문제에 대응하여 적절한 수준의 투입량을 산출하고 이를 위한 재공 소진 시스템에 대한 연구가 필요하게 되었다. 이에 본 논문에서는 센서와 기판의 1:1 조합 문제를 고려하여 재공 부족으로 인한 생산량 감소를 최소화하는 최적화 모델을 수립하고 재공 소진 시스템 기반의 투입량을 산출하여 재공을 설비에 할당하는 스케줄링 기법을 제안하고자 한다. 본 논문에서 제안된 스케줄링 모델을 통해 이미지 센서 제품을 생산하기 위해 필요한 공정들의 재공과 설비 가용능력 제약을 반영하였으며, 특히 재공 부족을 최소화하기 위한 투입량 결정 로직을 통해 수요 변동에 대응할 수 있도록 하였다.
반도체 생산 프로세스에서 재공을 효율적으로 사용하고자 하는 전략 수립은 매우 중요한 문제이다. 불필요하게 쌓이는 재공들로 인해 제조공기가 길어지게 되고 다음 공정으로 진행하지 못하면서 정체된 재공들이 불량을 발생시키는 요인이 되기 때문이다. 다양한 스케줄링 수립이 생산성과 시스템 성능에 미치는 영향을 실험적으로 분석한 연구가 진행되었으며[2], 반도체 웨이퍼 제조 공정에서 생산 계획 수립을 위한 다중 신뢰도 시뮬레이션 최적화 기법에 대해서도 제안되었다[3]. 반도체 공정에서 재공 로트 투입을 위한 대기열 네트워크 모델을 제안하여 총 생산 가용시간을 최소화하고자 하는 연구도 제안되었다[4]. 생산량을 높이기 위해 웨이퍼를 과도하게 투입하면 설비의 과부하를 초래하여 생산량 저하와 제조공기가 증가하는 문제가 생기게 되는데 이러한 현상을 해결하기 위해 웨이퍼-고객수요를 매칭한 웨이퍼 할당 최적화 모형과 혼합정수계획법 기반의 웨이퍼 용량 할당 문제를 풀기 위한 연구가 진행되었다[5][6]. 재공 밸런스를 위한 공정 간 적정재공의 양을 산출하여 적용하였고[7], 이미지 센서 제품을 대상으로 로직 칩과 픽셀 칩의 재공 매핑을 통해 생산량을 최대화할 수 있도록 하는 최적화 모델에 대한 연구도 진행이 되었다[8].
스케줄링은 투입규칙과 디스패칭 방법론으로 나눌 수 있으며, 이 두 가지 방법론에 대한 다양한 연구가 이루어졌다. 반도체 생산 공정 중 Furnace 공정은 고온에서 산화막을 형성하는 과정으로, 단일 웨이퍼가 아닌 여러 웨이퍼가 동시에 투입되므로 배치 처리가 매우 중요하다[9]. 다양한 제약 조건을 고려한 작업 스케줄링이 제시되었으며[10], 로트 로딩 시퀀스를 최적화하여 생산량을 극대화하는 스케줄링 모델이 개발되고 실험을 통해 검증되었다[11]. 반도체 웨이퍼 테스트 공정을 대상으로 실시간 데이터를 모니터링하고 제품의 품질을 관리하기 위한 연구도 진행되었다[12].
본 논문에서는 센서와 기판이 결합되어 최종 이미지 센서 제품으로 만들어지는 제조 특성을 반영하여 최적화 모형(고객 수요 최대화)을 수립하고, 생산라인에 있는 재공을 효율적으로 소진하기 위한 투입량 결정 로직을 개발하였다. 2장에서는 본 연구에서 제안하는 방법론에 대한 문제 정의를 서술하였으며, 3장에서는 제안된 연구에 대한 실험을 진행하여 적용 가능성을 위한 결과를 분석하였다. 마지막으로 4장에서는 결론을 정리하고 추후 연구 방향을 기술하였다.
Ⅱ. 문제 정의 및 모델링
2.1 이미지 센서 제품의 제조 특성
이미지 센서와 같은 반도체 제품을 생산하기 위한 Fabrication 공정은 전체 생산량을 결정짓는 대표적 병목공정이다. 설비 가용량, 제조공기 및 재공 현황이 고려되어 물류의 흐름이 결정되는데, 특히 고객 수요 다변화에 의한 혼류 제품 물류 흐름과 공정 내 공유설비 점유 이슈를 고려하여 생산정책을 수립하는 것이 매우 중요하다.
라인 내에 재공들이 적체되어 다음 공정으로 진행되지 못할 경우 제품의 결함이 발생하고, 품질 수율(Yield)을 유지하지 못하게 됨에 따라 생산량(양품) 저하가 발생한다. 그리고 고객의 수요 만족 차원에서 마지막 공정 기준으로 가장 가까이에 있는 공정에 위치한 재공들을 우선 소진함으로써 수요 납기준수 문제를 해결할 수 있다. 특히 이미지 센서 제품은 공정 내에 센서와 기판이 동일한 수준으로 재공이 존재해야 1:1로 조합되어 최종 완성품으로 출하가 가능하다. 이미지 센서는 일반적으로 반도체 생산 프로세스와 유사하게 물량이 이동하지만, Fabrication 공정에서 센서(Pixel)와 기판(Logic substrate)의 1:1 부품 조합으로 최종 제품이 생산된다. 센서는 반도체 프로세스를 통해 생산된 칩이며, 센서의 전력을 조절하는 회로 장치인 기판과 결합하여 하나의 이미지 센서가 만들어지게 된다.
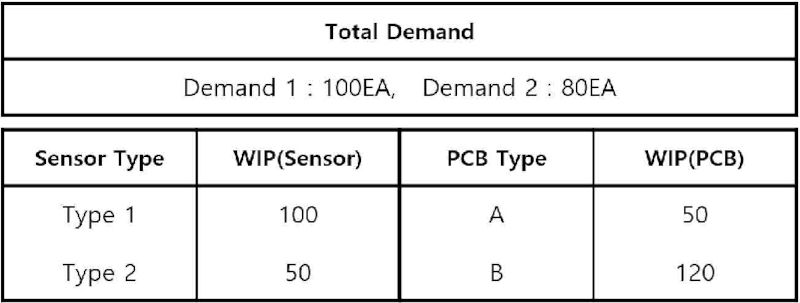
표 1에서는 고객 수요에 맞춰 최종 센서 제품을 생산하기 위한 센서 타입과 기판의 재공 현황을 보여주고 있다[9]. 고객 수요를 만족하기 위해 수요 1과 2는 각각 100개와 80개의 최종 제품이 필요하다. 센서 타입 1은 기판 A와 결합(Sensor Type 1 : PCB Type A)되고 센서 타입 2는 기판 B와의 조합을 통해 두 개 타입의 최종 이미지 센서 제품으로 생산된다. 수요 1의 경우 100개의 최종 생산품이 필요한데, 이를 만족시키려면 100개의 센서 타입 1의 재공과 100개의 기판 A 재공이 필요하지만 기판 A의 재공이 50개만 존재하므로 최종 제품으로 50개가 가능하고 기판 A의 재공은 50개가 남게 된다.
이는 고객 수요 1을 만족시키기 위해 추가로 50개의 기판 A 재공이 투입되어야 함을 의미한다. 고객 수요 2는 80개가 생산되어야 고객이 요청한 수요를 만족시킬 수 있지만 센서 타입 2의 재공이 50개, 기판 B의 재공은 120개가 존재하므로 최종 고객 수요를 충족시키지 못하고(30개의 재공 부족분) 70개의 기판 B 재공이 공정에 남게 되는 현상이 발생한다. 본 논문에서는 선형계획법 기반의 최적화 모델을 통해 수요에 따른 생산량 최대화 문제를 해결하고자 하였으며, 센서와 기판의 조합, 가용 및 부족 재공 등의 제약 조건을 반영한 재공 우선 소진 시스템을 적용한 투입 스케줄링 모델을 제안하고자 한다.
Indices
b : 센서와 기판의 재공 인덱스 ( b = 1, 2, ···, B )
k : 센서와 기판의 조합 가능 인덱스 ( k = 1, 2, ···, K )
c : 센서와 기판이 조합된 인덱스 ( c = 1, 2, ···, C )
Parameters
Dc : 센서와 기판 조합 c의 수요량
WIPb : 센서와 기판 b의 재공 수준
Rc,k,b : 재공 b, 조합 k, 조합된 제품 c의 수
Ub : 조합되지 못한 잉여 재공 b
Decision Variables
Xc,k : 조합 가능한 k, 조합된 제품 c의 생산량
Xc : 제품 c의 생산량
이미지 센서 제품을 대상으로 센서와 기판이 1:1 조합이 가능한 재공들을 고려하여 고객 수요 만족과 생산량을 최대화하는 프로세스 모델링을 위한 인덱스 및 목적함수와 제약조건을 구성하였다.
| (1) |
목적함수 식 (1)은 고객 수요를 만족시키기 위해 센서와 기판 조합에 의한 이미지 센서 제품의 생산량이 최대화되도록 정의하였다.
| (2) |
| (3) |
| (4) |
| (5) |
식 (2)는 초과생산으로 인해 불필요한 재고가 발생되지 않기 위해 고객 수요량이 생산량보다 크도록 하는 제약조건이며, 식 (3)은 센서와 기판의 재공들과 조합되지 않고 남아있는 재공까지 포함된 수가 전체 재공의 수를 초과할 수 없도록 하는 제약을 표현하고 있다.
식 (4)에서는 센서와 기판 부품이 1:1로 조합된 수가 전체 제품 생산량과 동일하도록 식 (4)를 모델링하였고, 마지막 식 (5)에서는 변수들의 비음조건을 나타내고 있다.
2.2 재공 소진 시스템 투입량 산출 기법
반도체 생산라인에서 수요충족률을 최대화하기 위해서는 공정 내 재공을 효율적으로 소진하면서 재공 부족분에 대응하기 위한 투입량을 산출하여 적용하는 것이 매우 중요하다. 생산량 대비 재공이 많으면 적체된 재공이 제품의 불량을 야기함과 동시에 제조공기가 길어지게 된다. 반대로 재공이 부족하면 생산량이 저하되어 고객 주문 납기를 충족하지 못하는 문제가 발생하기 때문이다.
반도체 생산라인에서 수요충족을 최대화하기 위해서는 마지막 공정 기준 가장 가까이 위치한 공정의 재공부터 우선적으로 소진하고 모두 소진되면 앞 공정의 재공들을 탐색하여, 재공 부족분에 대응하는 재공 투입량을 산출하는 작업이 매우 중요하다. 특히 이미지 센서 제품의 경우에는 센서 기판과 회로 기판이 1:1로 결합되어 생산되므로 공정 내에 각 재공들이 적절한 수준으로 준비되어 있어야만 수요 만족을 위한 최종 제품 생산이 가능하다.
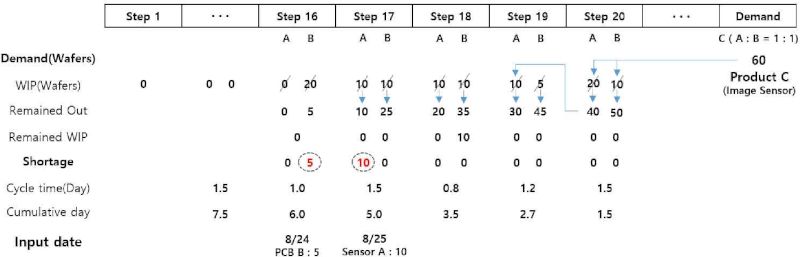
그림 1은 이미지 센서 제품을 생산하기 위해 재공을 소진하는 투입량 산출 로직을 도식화하여 보여주고 있다.
가장 마지막 공정을 거쳐 생산된 제품이 이미지 센서 최종 생산량이 된다. 최종 제품 C는 고객 수요를 만족시키기 위한 이미지 센서 수요량 60개를 의미한다. 8월 30일 기준 제품 C 60개가 생산되어야만 수요를 충족시킬 수 있다. 가장 마지막 공정인 Step 20으로부터 각 공정들에 위치하는 재공들을 순차적으로 차감하면서 계산을 하는데, 가장 마지막 공정에 센서 재공(A)은 20개, 기판 재공(B)은 10개가 위치하고 있다. 마지막 공정에서 센서 재공 20개, 기판 재공 10개를 차감하고 남은 제품 수량은 각각 40개, 50개가 된다. 해당 수량은 다시 앞 공정을 탐색하고 공정 내 재공이 있으면 재공을 차감하는 작업을 진행하게 되는데, 공정 19에서는 각 재공들이 10개, 5개가 존재하여 해당 재공들을 차감하고 생산되어져야 할 수량은 각 30개, 45개로 변경된다.
역행으로 각 공정들을 탐색하면서 가용한 재공들을 우선적으로 차감하면서 진행하게 되며, 공정에서 필요한 재공의 수량만큼 남은 일수를 계산하여 투입일자와 투입수량을 결정하게 된다. 그림 1의 도식화된 모형에서는 공정 16에서 재공 20을 차감하고 5개의 잔여 생산량이 생산 부족분(Shortage)으로 계산됨을 보여주고 있다. 공정 16에서 기판 재공 5개의 부족량은 8월 24일 기준으로 발생하게 되는데, 가장 마지막 공정으로부터 각 공정의 프로세싱 타임을 역행(공정 20 → 공정 16)으로 누적 계산하여 생성된 시간 6일을 반영하였기 때문이다. 공정 16 기준으로 발생된 기판 재공 부족분 5개는 공정 1부터 공정 15까지의 누적 프로세싱 타임을 고려하여 투입 일자를 산출하게 된다. 예를 들어, 공정 1부터 공정 15까지의 누적 프로세싱 타임이 15일이라면 기판 재공 부족분 5개는 8월 9일에 투입하면 된다. 물론 역행으로 공정들을 탐색하면서 차감 가능한 재공들이 있을 경우 위의 재공 차감 로직을 적용하여 투입일자와 수량을 재산출하여 새로운 정보로 업데이트 한다.
투입량 산출 및 재공 할당 룰
Step 1 : 재공 할당 로직을 위한 첫 단계로 제품, 스텝, 싸이클 타임, 작업 가능 설비들을 정의한다.
i = 제품, j = 스텝, k = 설비, t = 생산 일자(day)
WL(k, t) = t 기간 설비 작업 부하량
TI(i, j, t) = t 기간, j 스텝의 제품 i 투입량
C(i, j, k) = j 스텝, k 설비에서 생산될 i 제품 수
AT(k, t) = t 기간, k 설비의 작업 가용 시간
W/T(k) = k 설비의 작업 가능 시간
CT(i, j) = i 제품, j 스텝의 싸이클 타임
역행 전진을 통해 초기 투입량 산출한 뒤, 설비의 작업 부하도를 계산한다.
| (6) |
Step 2 : 작업 부하량에 의한 설비 우선순위에 따라 마지막 공정으로부터 재공을 우선적으로 소진하고 재공이 없으면 산출된 투입량을 설비 k에 할당한다.
| (7) |
Step 3 : 설비에 할당된 투입량이 모두 소진될 때까지 위의 프로시져를 반복하여 적용한다.
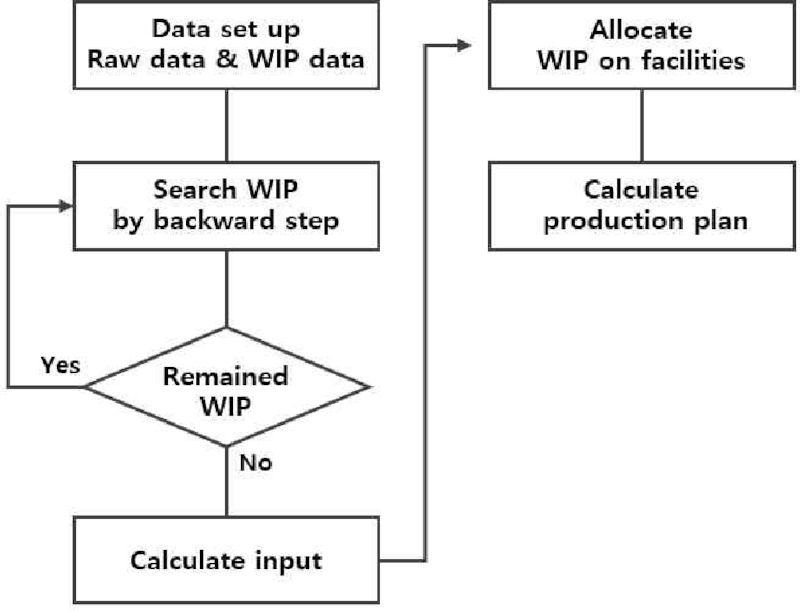
그림 2에서는 본 논문에서 제안하는 재공 소진 기반의 투입량 결정 시스템의 알고리즘을 도식화하여 보여주고 있다. 최적화 모델링에 의한 고객 수요량 기반으로 기준정보 데이터를 셋팅한다. 공정의 스텝들을 탐색하면서 사용 가능한 재공들을 찾아 우선적으로 소진하고 없으면 투입량을 산출하는데, 더 이상 소진 가능한 재공들이 없을때까지 반복하여 수행한다. 계산된 투입량들은 설비의 작업 부하도를 고려하여 할당되고 고객 수요량을 충족시킬 수 있도록 위의 프로시져를 반복하여 진행한다.
Ⅲ. 실험 결과
본 논문에서 제안한 재공 소진 시스템에 따른 초기 투입량 산출 모형의 타당성을 검증할 수 있도록 실제 반도체 라인을 단순화하여 모델링 하였다. 데이터 구성은 20개 공정에 30대 설비를 가정하였으며, 총 20개의 제품이 혼합되어 생산될 수 있도록 했다. 재공이 투입되어 생산되는데 소요되는 시간인 t는 30일, 설비의 하루 가동률은 시간으로 환산하여 1,440분(24시간×60분)으로 정의하였다. 하나의 제품이 생산되는데 소요되는 시간은 균등분포(Uniform distribution)를 적용하여 [1.0, 2.6]분 사이에서 생성하였다. 공정별 진행 시간은 [1.3, 1.7]분, 모든 공정 스텝을 거쳐 최종 생산되는 시간은 [30, 45]일 사이의 값을 갖도록 정의했다. 실험은 6개 케이스를 대상으로 진행하였으며, 케이스 1번부터 3번은 평균 수요량을 고정하였고, 케이스 4번에서 6번까지는 평균 수요량에 2배를 하고 값에 난수를 적용하여 매일의 생산 목표량을 생성하였다. 케이스 1번과 4번의 경우 평균 수요량을(125, 125, ... , 125)로 하였고, 케이스 2번과 5번은 평균 수요량을 200과 500으로, 케이스 3번과 6번은 (10, 20, 30, ... , 200)으로 정의하였다. 제품의 최종 생산량은 마지막 공정을 거쳐 생산된 양을 의미한다.
본 논문에서 제안된 재공 소진 시스템을 통해 생산라인 내 재공을 최우선적으로 소진하여 설비의 효율성을 높이고 부진재고(재공)를 최소화함과 동시에 생산량을 극대화하고자 한다. Target In Rule은 제안된 내용과 같이 가장 마지막 공정부터 역행 전진하면서 재공을 우선 차감한 후 재공 부족분이 발생할 경우 투입량을 산출할 수 있도록 하였으며, CONWIP 룰은 최종 생산량과 동일하게 투입량을 결정하였다.
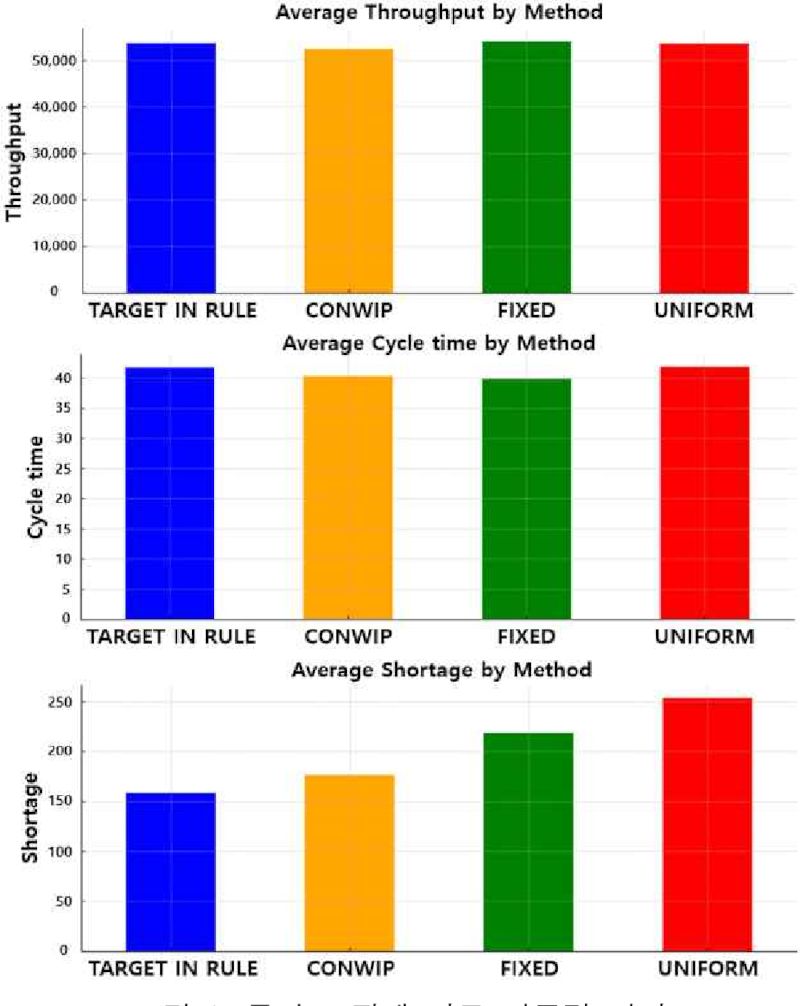
FIXED는 매일 각 제품들의 평균 수요량이 투입될 수 있도록 하였고, UNIFORM 규칙은 제품의 평균 수요량을 반영하여 무작위로 투입량을 결정하여 투입되도록 설정하였다. Throughput은 마지막 공정을 거쳐 나온 최종 생산량을 의미하며, Cycle time은 재공이 첫 공정으로 투입되어 마지막 공정을 거쳐 최종 제품 생산되는데 소요되는 총시간, Shortage는 재공 부족량으로 고객 수요에 충족되지 못하는 양을 의미한다. 표 2에서는 본 연구에서 제안된 역행 전진 재공 소진 시스템(Target In Rule)을 통해 계산된 생산 수요량과 각 투입 로직에 의한 재공 투입량을 적용하여 진행된 실험 결과를 보여주고 있다. Throughput의 경우 FIXED 방식이 54,035로 가장 높은 평균 생산량을 보였으며, 자원 활용과 생산 효율성 측면에서 가장 우수한 결과를 보여주었다.
CONWIP 방식은 52,463로 가장 낮은 평균 생산량을, Target In Rule 방식은 53,737개의 평균 생산량을 달성함으로써, FIXED 방식 대비 약 0.01% 정도의 생산 차질이 발생하였으나, 평균 생산량 측면에서 근소한 차이가 발생되었다.
Cycle time에서는 FIXED 방식이 39.84로 가장 낮아 작업 속도와 효율성이 가장 뛰어난 것으로 평가되었다. 고객 수요충족에 가장 중요한 핵심지표 중 하나인 Shortage에서는 Target In Rule 방식이 159로 가장 낮은 수치를 보여주었다. FIXED 방식과 UNIFORM 방식은 상대적으로 높은 재공 부족분 결과를 기록하여 수요 관리 측면에서는 약점을 드러내었다.
실험 결과를 보면, Case 2에서 평균 수치 대비하여 약 50% 정도의 개선된 결과를 보여 주었는데, 이는 초기 재공값이 전체 공정에 균일하게 분포하고 있어 적은 투입량으로도 수요를 충족시킬 수 있었음을 의미한다.
Shortage 평가지표는 센서와 기판이 1:1 조합되어 단일 제품으로 생산되지 못하는 고객 수요 대비 부족분이며, 1:1 조합이 되지 못하는 잉여 재공 발생으로 인해 생산 차질이 발생될 수도 있음을 의미한다. 본 논문에서 제안하는 Target In Rule 로직은 Throughput과 Cycle time 평가지표에서 균형 잡힌 결과를 보여 전반적으로 안정적인 성과를 기대할 수 있었고, 특히 생산량 관점에서 18.8% 이상의 생산지표 결과를 보여줌으로써, 수요충족이 중요한 제조 환경에서 매우 적합한 생산정책으로의 적용이 가능하다. FIXED 방식은 생산성과 작업 효율을 극대화할 수 있는 환경에 적합하지만, Shortage 물량이 너무 높아 수요충족 부분에 있어 최대 약점을 갖게 된다. 특히 고객 수요 변동이 심할 경우 재공 투입량의 추가적인 조정이 필요할 수 있다. 그림 3에서는 각 투입 전략에 따른 평가지표의 평균값 결과를 보여주고 있다.
Ⅳ. 결론 및 향후 과제
4차 산업혁명의 가속화 현상이 고성능 반도체 제품의 성장을 견인하고 있으며, 특히 스마트폰과 자율주행 자동차 등에 사용되는 이미지 센서 제품의 사용량도 같이 증가하고 있다. 이에 본 논문에서는 이미지 센서 제품의 생산량을 높이고 고객 수요 만족을 최대화 할 수 있는 재공 소진 시스템을 제안하였으며, 전통적인 투입량 결정 로직인 CONWIP, FIXED, UNIFORM과의 비교 분석을 통해 제안된 시스템의 적용 가능성을 평가하였다. 특히 본 연구는 생산라인에서 발생하는 재공 부족으로 인한 생산량 감소 현상을 해결하고, 생산성과 고객 만족도를 동시에 향상시키는 데 중점을 두었다. 그러나 본 연구는 몇 가지 한계를 내포하고 있다. 본 연구에서 사용된 데이터와 실험 환경은 실제 생산 공정을 최대한 반영하고자 하였으나, 반도체 제조와 같은 복잡한 공정 특성과 물류 흐름, 생산 비용 등 현실적인 제약 조건을 모두 반영하기에는 한계가 있었다. 특히 반도체 제조 분야에서는 방대한 양의 데이터를 기반으로 최적의 투입규칙과 생산 계획을 수립하는 연구가 지속적으로 이루어지고 있어, 이를 통합적으로 적용할 필요성이 있다.
향후 연구에서는 실제 이미지 센서 제품의 제조 데이터를 기반으로 한 실험 환경을 구축하고, 반도체와 같은 복잡한 생산 시스템의 물류 흐름과 제약 조건을 포함한 시뮬레이션 모델을 개발하고자 한다. 이를 통해 실제 생산 환경에서 발생하는 변수와 제약 조건이 정교하게 반영된 최적화 투입규칙을 수립하고, 효율적인 재공 관리를 통해 생산성과 고객 만족도를 동시에 달성할 수 있는 종합적인 생산 시스템을 제안하고자 한다.
References
-
S. S. Park, B. J. Shin, and H. S. Uh, "Recent Technology Trends and Future Prospects for Image Sensor", Journal of the Microelectronics and Packaging Society, Vol. 27, No. 2, pp. 1-10, Jun. 2020.
[https://doi.org/10.6117/kmeps.2020.27.2.01]

-
R. Singh and M. Mathirajan, "Experimental investigation for performance assessment of scheduling policies in semiconductor wafer fabrication - a simulation approach", The International Journal of Advanced Manufacturing Technology, Vol. 99, No. 23, pp. 1503-1520, Aug. 2020.
[https://doi.org/10.1007/s00170-018-2414-y]

-
F. Zhang, J. Song, Y. Dai, and J. Xu, "Semiconductor wafer fabrication production planning using multi-fidelity simulation optimisation", International Journal of Production Research, Vol. 58, No. 21, pp. 6585-6600, Jan. 2020.
[https://doi.org/10.1080/00207543.2019.1683252]

-
O. Bernhard, R. Boualem, and R. Gerald, "Optimization lot priority rules in semiconductor production system", IFAC-PapersOnLine, Vol. 52, No. 13, pp. 1260-1265, Oct. 2019.
[https://doi.org/10.1016/j.ifacol.2019.11.371]

-
C. D. Patrik, A. Jelle, and A. Alp, "Optimizing class-constrained wafer-to-order allocation in semiconductor back-end production", Journal of Manufacturing System, Vol. 57, pp. 72-81, Oct. 2020.
[https://doi.org/10.1016/j.jmsy.2020.07.022]

-
G. Amir, A. Radhia, L. Georg, E. Kamil, and H. athal, "Optimizing capacity allocation in semiconductor manufacturing photolithography area-case study:Robert Borch", Journal of Manufacturing System, Vol. 54, pp. 123-137, Jan. 2020.
[https://doi.org/10.1016/j.jmsy.2019.11.012]

-
B. Lee, Y. H. Lee, T. Yang, and J. Ignisio, "A due-date based production control policy using WIP balance for implementation in semiconductor fabrication", International Journal of Production Research, Vol. 46, pp. 5515-5529, Feb. 2008.
[https://doi.org/10.1080/00207540701369213]

-
J. W. Kim, "A Study on Efficient Process Policy for Satisfying Demand of Image Sensor", Journal of KIIT, Vol. 20, No. 12, pp. 175-183, Dec. 2022.
[https://doi.org/10.14801/jkiit.2022.20.12.175]

-
K. Dominik and M. David, "Semiconductor final-test scheduling under setup operator constraints", Computer & Operations Research, Vol. 138, pp. 391-401, Feb. 2022.
[https://doi.org/10.1016/j.cor.2021.105619]

-
W. Kan, H. Edward, W. Mengchang, and Z. Meimei, "Job scheduling of diffusion furnaces in semiconductor fabrication facilities", European Journal of Operational Research, Vol. 301, No. 1, pp. 141-152, Aug. 2022.
[https://doi.org/10.1016/j.ejor.2021.09.044]

-
M. Massimo and U. Marcello, "A scheduling approach for chemical vapor deposition processes in the production of semiconductors", IFAC-Papers On Line, Vol. 52, No. 13, pp. 505-510, Aug. 2019.
[https://doi.org/10.1016/j.ifacol.2019.11.116]

-
W. Fu, C. Chein, and C. Chen, "Advanced quality control for probe precision forming for semiconductor manufacturing", Computer & Industrial Engineering, Vol. 183, pp. 168-176, Sep. 2023.
[https://doi.org/10.1016/j.cie.2023.109461]


2004년 2월 : 단국대학교 전자계산학(학사)
2007년 2월 : 연세대학교 산업시스템공학과(석사)
2011년 8월 : 연세대학교 정보산업공학과(박사)
2012년 6월 ~ 2024년 2월 : 삼성전자 혁신센터 연구원
2024년 2월 ~ 현재 : 선문대학교 경영학과 교수
관심분야 : 생산계획, SCM, 최적화