원형 사각 직교진폭변조의 비트열 매핑 및 채널용량 연구
초록
각 심볼의 평균 에너지 사용을 최소화하는 원형 사각 직교진폭변조(C-SQAM, Circular SQAM) 기법은 변조차수가 증가할수록 비트열(Bits-to-symbol) 매핑을 획득하기 위한 연산량이 계승 시간에 비례하여 증가한다는 문제점을 갖는다. 본 논문에서는 C-SQAM의 기존 비트열 매핑의 단점을 극복하는 그룹 검색 기반의 신규 비트열 매핑 방식을 제안하고, C-SQAM의 이론적 한계를 규명하기 위해 가산성 백색 가우시안 잡음(AWGN) 채널에서의 채널 용량을 분석한다. 결과에 따르면, 기존 비트열 매핑을 수행하기 위해 필요한 계승시간 복잡도는 제안 기법에 의해 제곱시간 복잡도로 완화되었고, C-SQAM의 채널 용량은 전반적인 영역에서 SQAM에 비해 개선되었다.
Abstract
Circular Square Quadrature Amplitude Modulation(C-SQAM) minimizing the average energy use of each symbol faces the problem that as the modulation order increases, the amount of computation to acquire bits-to-symbol mapping increases drastically. In this paper, we propose a group-search based bit string mapping scheme that overcomes the shortcomings of the existing mapping of C-SQAM and analyze the channel capacity of C-SQAM in the Additive White Gaussian Noise(AWGN) channel. According to the results, the factorial-time complexity of the conventional bit string mapping is mitigated to the square-time complexity by the proposed technique, and the channel capacity of C-SQAM is improved in a wide range compared to SQAM.
Keywords:
SQAM, C-SQAM, bits-to-symbol mapping, gray penalty, channel capacityⅠ. 서 론
이동통신 시스템은 5G까지 상용화되며 세부 기술에 있어 획기적인 개선이 있었고, 현재 차세대 이동통신 시스템 개발을 위해 활발한 연구가 수행되고 있다. 다양한 물리계층 전송 기술 중에서 고차 변조 기법, 직교진폭변조(QAM, Quadrature Amplitude Modulation)는 디지털 정보의 고속 전송을 가능하게 하며, 특히 Campoiano와 Glazer에 의해 제안된 사각 직교진폭변조(SQAM, Square QAM)는 비교적 낮은 복잡도를 가지면서도 우수한 비트오율 특성을 제공하기에 여러 상용 시스템에서 널리 사용되고 있다[1]. 한편, SQAM의 성능과 고차변조의 효율성을 개선하기 위한 다양한 연구가 진행되어 왔다[2]-[5].
최근 선행 연구에서 SQAM의 성상도를 변형하여 각 심볼의 평균 에너지 사용을 최소화하는 원형 사각 직교진폭변조(C-SQAM, Circular SQAM) 기법이 제안되었고, 이를 통해 SQAM 대비 0.2003 dB의 전력 이득이 발생하고 피크 대 평균 전력비(PAPR, Peak-to-Average Power Ratio)는 33% 감소함이 보고되었다[6]. 동 논문에서 C-SQAM을 구성하기 위한 비트열과 심볼 간 매핑 방법도 제시되었으나, 변조차수가 증가할수록 계산 복잡도가 급격히 증가하는 문제가 있었다. 예를 들어, 4096진 C-SQAM의 성상도를 설계하려면 비트열 매핑을 찾기 위해 20!에 달하는 검색이 필요하며 이는 실제 구현에 적합하지 않다.
이에 본 논문에서는 기존 비트열 대 심볼 매핑의 단점을 극복하는 C-SQAM의 신규 비트열 매핑 방식을 제안하고 결과를 분석한다. 또한, C-SQAM의 이론적 한계 규명을 위해 C-SQAM의 채널 용량을 도출하고 SQAM의 채널 용량과 비교, 분석한다.
본 논문의 구성은 다음과 같다. 2장에서는 논문의 가독성 제고를 위해 선행 연구에서 제안한 C-SQAM의 성상도 형성 방법과 비트열-심볼 매핑 등에 대해 개략적으로 소개한다. 3장에서 제안하는 비트열-심볼 매핑 방식에 대해 상세히 상술하고 기존 방식과 연산 복잡도 측면에서 비교한다. 4장에서 C-SQAM의 채널 용량을 가산성 백색 가우시안 잡음(AWGN, Additive white Gaussian noise) 채널 환경에서 도출하고 타 기법과의 비교 분석을 수행한다. 마지막으로 5장에서 결론을 기술한다.
Ⅱ. C-SQAM
2.1 성상도 형성
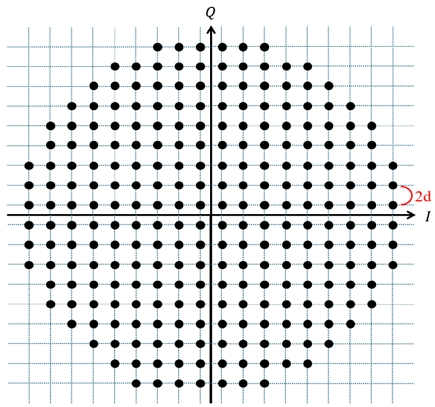
그림 1은 전송 에너지 효율을 개선하기 위해 제안된 256진 C-SQAM의 성상도이다[6]. C-SQAM에서는 인접한 심볼 간 최소 유클리드 거리가 2d인 사각 격자의 꼭지점에 성상점이 위치할 수 있으며, 평균 심볼 에너지(Es, Average symbol energy)를 최소화하도록 성상점이 선택된다. 따라서 변조차수 M이 증가함에 따라 C-SQAM의 외형은 점차 원의 형태에 가까워진다.
한편, 성상도 상의 임의의 심볼 si의 에너지는 다음 수식으로 계산되는데, 여기서 si,I 와 si,Q는 각각 si의 I축 성분과 Q축 성분을 의미한다.
| (1) |
식 (1)을 활용하여 M진 C-SQAM의 평균 심볼 에너지, Es를 다음과 같이 계산할 수 있다.
| (2) |
또한, 식 (2)을 활용하여 SQAM 대비 C-SQAM의 전력 이득(PG, Power Gain)을 다음과 같이 정의하고 계산할 수 있다.
| (3) |
표 1은 M에 따른 SQAM과 C-SQAM의 Es와 PG를 나타내며, M이 증가할수록 SQAM 대비 C-SQAM의 PG는 약 0.2 dB에 빠르게 수렴함을 확인할 수 있다.
2.2 비트열-심볼 매핑
M진 고차변조에서 각 변조심볼에 m (=log2M) 개의 고유한 이진 데이터 열을 할당하는 과정이 필요하다. SQAM에서는 인접한 심볼 간 서로 상이한 비트의 개수가 1인 그레이 부호를 I축과 Q축에 각각 독립적으로 사용하며, 이로 인해 인접 심볼 간 상이한 비트 개수의 평균을 나타내는 그레이 페널티(Gp, Gray penalty) 값은 항상 1이 된다. 그레이 패널티를 수식으로 정의하면 다음과 같다[7].
| (4) |
여기서 는 변조심볼 si와 이의 인접 심볼 간 상이한 비트 개수의 평균을 나타내며, N(si)는 변조심볼 si와 인접한 심볼의 개수를, D(si,sj)는 변조심볼 si와 인접심볼 sj 간 상이한 비트의 개수를 의미한다.
한편, 디지털 통신에서 채널을 통과할 때 전송 오류가 발생하며, AWGN 채널에서 심볼 오율(Ps, Symbol error rate)과 비트 오율(Pb, Bit error rate)을 다음과 같이 근사화할 수 있다[8].
| (5) |
여기서 η는 변조심볼의 평균 인접 심볼 수, Q(•)는 가우시안 Q함수, No/2는 잡음 전력 스펙트럼 밀도를 나타낸다. 비트오율 성능 개선을 위해서는 평균 심볼 에너지 Es 최소화와 더불어 비트열-심볼 매핑 연구를 통해 Gp 및 η를 개선해야 함을 식 (5)를 통해 확인할 수 있다.
SQAM 기법의 비트열 매핑에 있어 I축과 Q축 매핑이 서로 디커플링되어 있기에 항상 Gp = 1인 것과는 달리, C-SQAM에서는 불규칙적 성상도 형태로 인해 Gp = 1인 비트열 매핑이 존재하지 않으며 이에 Gp = 1에 근접하는 비트열 매핑 기법을 탐구할 필요가 있다. 일례로, [6]에서 제안된 C-SQAM의 각 사분면에 공통적으로 적용하는 비트열 매핑 방법은 다음과 같다.
[단계 1] SQAM 성상도와 C-SQAM 성상도를 비교하여 동일한 위치에 있는 SQAM 심볼의 비트열을 C-SQAM 심볼에 할당
[단계 2] 1단계 수행을 통해 비트열을 할당받지 못한 심볼들을 대상으로, Gp = 1을 유지하면서 가능한 한 많은 심볼에 비트열 할당
[단계 3] 1, 2단계 수행 후에도 미할당된 심볼들에 대해서 전체 검색(Full search)을 통해 Gp를 최소화하는 비트열 매핑을 찾음
상기 비트열 매핑 방법은 비교적 간단한 절차를 통해 낮은 Gp를 갖는 C-SQAM의 비트열 매핑을 설계하지만, M이 증가함에 따라 [단계 3]의 계산 복잡도 T(M)이 다음과 같이 계승 시간에 비례하여 급증하는 문제점을 갖는다.
| (6) |
여기서 n은 1, 2단계 수행 후에도 비트열이 할당되지 않은 잔여 심볼의 개수이다.
즉, 식 (6)은 n개의 미할당 심볼에 대해 임의로 비트열을 할당하고 Gp를 산출해보는 과정을 총 n!회 반복해야 Gp를 최소화하는 비트열 매핑을 획득할 수 있음을 의미한다. 구체적으로, M이 1024일 때 n = 4에 불과하여 [단계 3] 수행이 가능하지만, M이 4096일 때 n = 20에 달해 [단계 3]을 수행하기에 적합하지 않다.
Ⅲ. 그룹 검색 비트열 매핑
C-SQAM의 비트열 매핑에 요구되는 복잡도를 감소시키기 위해 1, 2단계 수행 후에도 비트열을 할당받지 못한 n개의 심볼을 그룹 단위로 구분한 후 그룹 내에서 비트열을 할당받을 순서를 정해 비트열을 할당하는 그룹 검색 기반 비트열 매핑 기법을 제시한다. 즉, 제안 기법에서는 II장에서 상술한 [단계 1]과 [단계 2]의 과정을 동일하게 수행한 후 다음의 후속 과정을 통해 비트열 매핑을 완성한다.
[단계 3] 서로 인접한 미할당 심볼들로 구성된 그룹들 중에서 심볼 개수가 가장 많은 그룹을 선택한 후, 그룹 내에서 비트열이 기할당된 인접 심볼이 많은 심볼 순서대로 Gp를 최소화하는 비트열 매핑을 탐색하여 할당
[단계 4] 남은 그룹이 없어질 때까지 3단계를 반복하여 수행
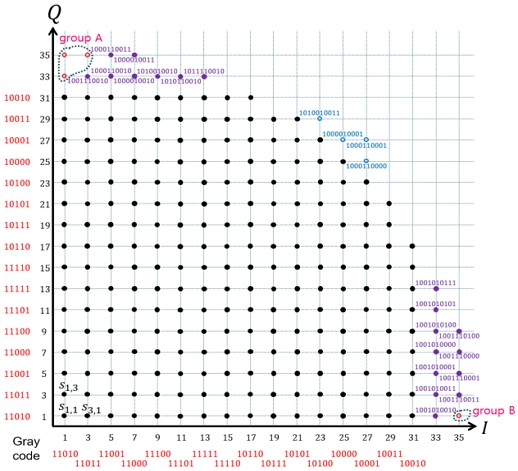
상기 절차를 예를 들어 설명하면 다음과 같다. 그림 2는 [단계 2]까지 진행된 1024진 C-SQAM 1사분면 성상도를 나타낸다. 그림에서 233개의 검은색 심볼은 [단계 1]의 결과로써, 해당 심볼들은 SQAM과 C-SQAM의 동일 위치에 공통적으로 존재하여 SQAM의 비트열 매핑을 C-SQAM에 그대로 인계하여 할당한다. 19개의 보라색 심볼은 [단계 2] 수행을 통해 비트열 할당된 심볼을 의미하며, 각 심볼의 위 또는 아래에 할당한 비트열을 표기하였다. 한편, 4개의 빨간색 심볼은 [단계 1]과 [단계 2] 수행 후에도 미할당된 C-SQAM 심볼들로 추후 비트열 할당이 필요하며, 4개의 파란색 심볼은 SQAM 심볼 중 C-SQAM 심볼의 비트열로 사용되지 않은 심볼들로 4개의 빨간색 C-SQAM 심볼들의 비트열 매핑을 위해 사용 가능한 잔여 비트열을 나타낸다.
그림 2에 나타내었듯이 비트열 할당이 필요한 4개의 C-SQAM 심볼은 인접 여부에 따라 좌측 상단과 우측 하단의 두 개의 그룹으로 구분된다. 즉, 각 심볼을 좌표 위치에 따라 si,j로 표기할 때, 첫 번째 그룹은 A= {s1,33, s1,35, s3,35}, 두 번째 그룹은 B = {s35,1}이 된다.
[단계 3]에 따라 크기가 더 큰 A 그룹의 비트열 매핑을 우선적으로 수행한다. A 그룹에 속하는 세 개의 심볼에 대해 s1,33의 기할당된 인접 심볼은 두 개(s1,31, s3,33) 존재하고, s1,35의 기할당된 인접 심볼은 없으며, s3,35의 기할당된 인접 심볼은 두 개(s3.33, s5,35) 존재한다. 따라서, [단계 3]에 따라 할당된 인접 심볼이 가장 많은 s1,33부터 비트열 매핑을 시도한다(s3,35와 동수이므로 랜덤하게 선택). 한편, s1,33에 할당될 수 있는 비트열은 파란색 심볼이 보유하고 있는 4개의 비트열(1010010011, 1000010001, 1000110001, 1000110000)이며, 각 비트열을 s1,33에 매핑하고 Gp를 계산하는 과정을 반복한 후 최소의 Gp 값을 갖는 비트열인 1000110000을 s1,33에 할당한다. 다음으로 s3,35에 할당될 수 있는 비트열은 잔여 3개의 비트열(1010010011, 1000010001, 1000110001)이며, 각 비트열을 s3,35에 매핑하고 Gp를 계산해본 후 최소의 Gp 값을 갖는 비트열인 1000110001을 s3,35에 할당한다.
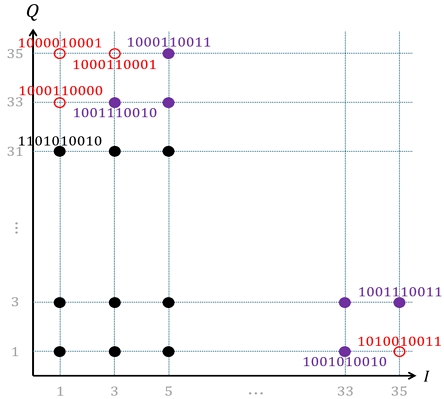
끝으로 s1,35에 할당될 수 있는 비트열은 잔여 2개의 비트열(1010010011, 1000010001)이며, 각 비트열을 s1,35에 매핑하고 Gp를 계산해본 후 최소의 Gp 값을 갖는 비트열인 1000010001을 s1,35에 할당하고 A 그룹의 비트열 매핑을 종료한다. 그 다음, [단계 4]에 따라 B 그룹의 비트열 매핑을 수행하며, B 그룹에 속한 유일한 심볼 s35,1에 대해 남아있는 비트열 1010010011을 최종적으로 할당한다. 그림 3은 상기 그룹 검색 기법을 적용하여 비트열 매핑을 완료한 1024진 C-SQAM 성상도의 일부를 나타낸다.
제안한 그룹 검색 기반 비트열 매핑을 완성하기위해 Gp를 계산해보는 횟수는 다음의 수식으로 표현될 수 있으며, 이는 곧 복잡도 O(n2)을 의미한다.
| (7) |
식 (6)과 (7)을 통해 도출한 복잡도와 획득한 매핑의 최종 그레이 페널티 Gp를 표 2에 수록하였다. M = 1024인 경우, 기존 방법에 의한 복잡도는 4!(=24), 제안 방법에 의한 복잡도는 10으로 약 58%의 연산량 감소 효과를 얻을 수 있었고, 기존 방법과 제안 방법의 비트열 매핑 결과가 서로 완전히 일치하여 동일한 Gp를 제공하였다. M = 4096인 경우, 기존 방법에 의한 복잡도는 20!에 달해 비트열 매핑이 불가하였으나, 제안 방법에 의한 복잡도는 210에 불과하여 최종적인 비트열 매핑을 획득할 수 있었다. 또한, M = 4096일 때 제안 기법의 Gp = 1.0309로 최적 값인 1에 근접하는 낮은 값을 유지함을 확인하였다.
Ⅳ. 채널 용량 분석
C. Shannon에 의해 도입된 채널 용량은 임의로 낮은 오류 확률로 채널을 통해 전송할 수 있는 정보의 최대 속도를 의미한다[9]. 정보 이론에서 점대점 이산 무기억 채널(Discrete memoryless channel)의 상호정보량(Mutual information)은 두 개의 확률 변수 X와 Y에 관한 확률질량함수들에 의해 다음과 같이 계산될 수 있다.
| (8) |
여기서 X와 Y는 각각 채널의 입력과 출력을 나타내는 유한 집합이며, 채널 용량은 X와 Y간 상호정보량의 최대값으로 정의된다.
| (9) |
입력 심볼과 신호 대 잡음비(SNR, Signal-to-noise ratio)를 가진 AWGN 채널의 상호정보량에 대한 근사 수식에 Gaussian-Hermite Quadrature 적분 방법을 적용하면 다음의 수식으로 채널 용량을 근사화하여 계산할 수 있다[10][11].
| (10) |
여기서 xm과 는 각각 송신 및 수신 심볼을 나타낸다. N은 신호 공간의 차원이고 Z는 신호에 가해지는 복소 가우시안 잡음이다.
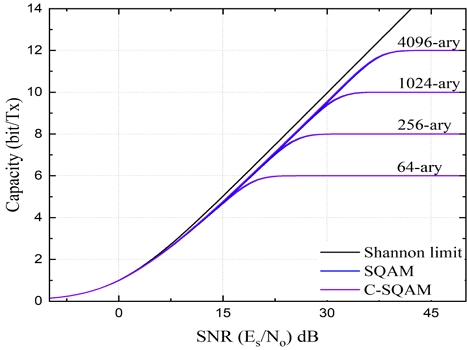
그림 4는 식 (10)을 통해 얻은 SQAM과 C-SQAM의 채널 용량 그래프이다. 검은색 실선은 Shannon limit이며, 파란색 실선과 보라색 실선은 각각 SQAM과 C-SQAM을 나타낸다. 현재의 그래프에서는 SQAM과 C-SQAM의 성능 차이를 명확히 구분하기 어렵기에 보다 상세히 분석해볼 필요가 있다.
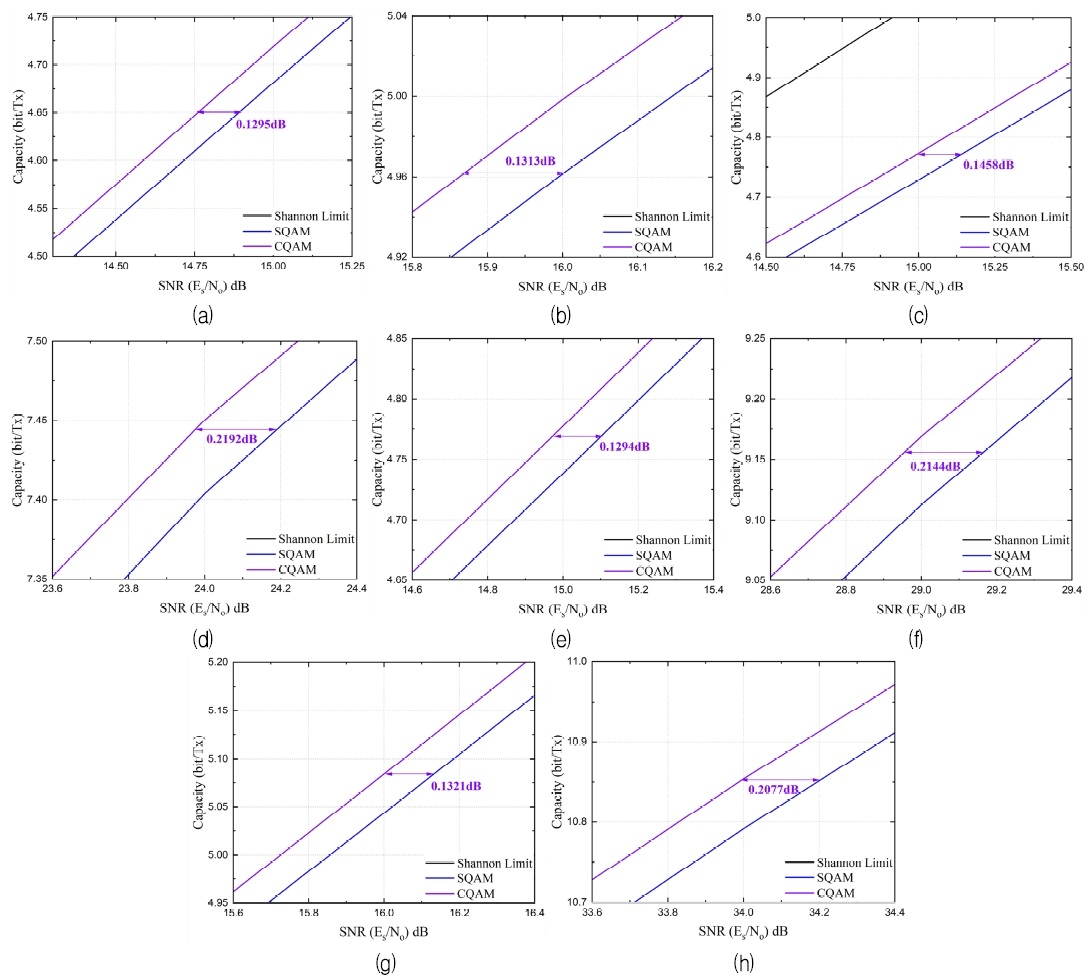
그림 5는 M=64, 256, 1024, 4096의 채널 용량이 증가하는 영역에 대해 낮은 SNR 영역과 높은 SNR 영역으로 구분한 후 확대하여 나타낸 그래프이다.
결과에 따르면, 변조차수에 관계없이 낮은 SNR보다 높은 SNR에서 C-SQAM의 이득이 증가함을 확인할 수 있다. 일례로 C-SQAM은 SQAM 대비 0.1313 dB, 0.2192 dB, 0.2144 dB, 0.2077 dB의 성능 개선을 얻음을 고찰하였다. 상기 영역에서 C-SQAM의 채널 용량이 개선되는 원인은 표 1에 간접적으로 나타내었듯이 동일한 심볼 에너지 사용을 가정할 때 C-SQAM의 성상점간 거리가 SQAM의 성상점간 거리보다 더 멀기 때문이다.
Ⅴ. 결 론
본 연구에서는 C-SQAM 기법을 위한 그룹 검색 기반 비트열-심볼 매핑 방법을 제안하고 복잡도를 분석하였다. 기존 비트열 매핑의 복잡도는 O(n!)로 M = 4096의 비트열 매핑이 현실적으로 불가하였으나, 제안 방법은 비트열 매핑의 복잡도를 O(n2)로 대폭 완화하여 M = 4096 C-SQAM의 비트열 매핑을 가능하게 하였다. 아울러 제안 방법에 따른 비트열 매핑의 Gp는 1에 근접하는 낮은 값을 제공함을 확인하였다. 또한, 채널 용량 분석을 수행하여 채널 용량이 점차 증가하는 SNR 영역에서 C-SQAM이 SQAM 대비 약 0.2 dB의 개선이 있음을 검증하였다. 본 연구에서 제안한 그룹 검색 기반 비트열 매핑 기법은 C-SQAM에 한정되지 않으며 다양한 형태를 갖는 타 성상도의 비트열 매핑에 활용될 수 있을 것이다.
References
-
C. Campopiano and B. Glazer, "A coherent digital amplitude and phase modulation scheme", IEEE Transactions on Communications, Vol. 10, No. 1, pp. 90-95, Mar. 1962.
[https://doi.org/10.1109/TCOM.1962.1088634]

-
G. Foschini, R. Gitlin, and S. Weinstein, "Optimization of two-dimensional signal constellations in the presence of Gaussian noise", IEEE Transactions on Communications, Vol. 22, No. 1, pp. 28-38, Jan. 1974.
[https://doi.org/10.1109/TCOM.1974.1092061]

-
G. Forney, R. Gallager, G. Lang, F. Longstaff, and S. Qureshi, "Efficient modulation for band-limited channels", IEEE Journal of Selected Areas Communications, Vol. 2, No. 5, pp. 632-647, Sep. 1984.
[https://doi.org/10.1109/JSAC.1984.1146101]

-
S.-J. Park, "Triangular quadrature amplitude modulation", IEEE Communications Letters, Vol. 11, No. 4, pp. 292-294, Apr. 2007.
[https://doi.org/10.1109/LCOM.2007.348278]

-
S. Kim, "An Euclidean diatance-based power allocation algorithm with reduced complexity for quadrature spatial modulation systems", Journal of KIIT, Vol. 17, No. 10, pp. 33-39, Oct. 2019.
[https://doi.org/10.14801/jkiit.2019.17.10.33]

-
M. Seong and S.-J. Park, "Quadrature amplitude modulation with circular boundary", Journal of KICS, Vol. 47, No. 6, pp. 801-806, Jun. 2024.
[https://doi.org/10.7840/kics.2024.49.6.801]

-
P. K. Singya, P. Shaik, N. Kumar, V. Bhatia, and M.-S. Alouini, "A survey on high-order QAM constellations: technical challenges, recent advances, and future trends", IEEE Open Journal of the Communications Society, Vol. 2, pp. 617-655, Mar. 2021.
[https://doi.org/10.1109/OJCOMS.2021.3067384]

-
E. N. Gilbert, "A comparison of signaling alphabets", The Bell System Techical Journal, Vol. 31, No. 3, pp. 504-522, May 1952.
[https://doi.org/10.1002/j.1538-7305.1952.tb01393.x]

- R. B. Ash, "Information Theory", Dover Publication, 2012.
-
A. G. Fabregas and G. Caire, "Coded modulation in the block-fading channel: coding theorems and code construction", IEEE Transactions on Information Theory, Vol. 52, No. 1, pp. 91-114, Jan. 2006.
[https://doi.org/10.1109/TIT.2005.860414]

- M. Abramowitz and I. A. Stegun, "Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables", U.S. Government Printing Office, 1968.

2022년 2월 : 강릉원주대학교 전자공학과(공학사)
2024년 2월 : 강릉원주대학교 전자공학과(공학석사)
2024년 3월 ~ 현재 : 연세대학교 소프트웨어학부 연구조교수
관심분야 : 디지털통신, 무선통신, 인공지능 기술

1996년 2월 : 연세대학교 전파공학과(공학사)
1998년 2월 : 한국과학기술원 전기및전자공학과(공학석사)
2004년 2월 : 한국과학기술원 전자전산학과(공학박사)
2005년 4월 ~ 현재 : 강릉원주대학교 전자반도체공학부 교수
관심분야 : 디지털통신, 무선통신, 이동통신