특성 확장을 이용한 태양광 발전량 예측을 위한 딥러닝 모델
초록
무한한 에너지원을 가진 태양광 발전은 기상 환경에 의존하기 때문에 발전량이 간헐적이어서 효율적인 에너지 관리를 위해서 발전량의 불확실성을 줄이고 경제성을 향상하기 위하여 정확한 발전량 예측 기술이 필요하다. 본 논문은 특성 공학을 이용하여 입력 특성을 확장하고, 다양한 딥러닝 모델을 통해 태양광 발전량을 예측하였다. 제안한 딥러닝 모델은 기본 딥러닝 모델을 병렬로 연결한 모델로서 DNN 모델을 기본으로 1D-CNN, Multi kernel 1D-CNN을 병합한 DCNN, DMCNN 모델과 LSTM, BiLSTM을 병합한 DLSTM, DBiLSTM 모델이다. 실험 결과, 기본 모델에서는 특성공학을 적용한 모델의 오차가 적었으며, 기본 모델 보다 병렬 모델의 오차가 적었다. 특히, 병렬 모델 중에서도 DBiLSTM 모델이 본 논문에서 제시한 모델 중 가장 뛰어난 성능을 보였으며, 영암 발전소에서의 RMSE는 0.0326, 연성 발전소에서의 RMSE는 0.0231로 나타났다.
Abstract
Solar power generation, which relies on an infinite energy source, is intermittent due to its dependence on weather conditions. Therefore, accurate power generation prediction technology is essential to reduce the uncertainty of power generation and enhance economic efficiency for effective energy management. This paper expands input features using feature engineering and predicts solar power generation through various deep learning models. The proposed deep learning models are parallel models that connect basic deep learning models in parallel, including the DCNN and DMCNN models, which merge 1D-CNN and Multi-kernel 1D-CNN based on the DNN model, and the DLSTM and DBiLSTM models, which merge LSTM and BiLSTM. The experimental results showed that the models applying feature engineering had lower errors in the basic models, and the parallel models had even lower errors than the basic models. In particular, among the parallel models, the DBiLSTM model demonstrated the best performance of all the models proposed in this paper, with an RMSE of 0.0326 for the Yeong-am Power Plant and an RMSE of 0.0231 for the Yeon-seong Power Plant.
Keywords:
solar photovoltaic generation forecast, deep neural network, parallel modelⅠ. 서 론
신재생 에너지는 햇빛, 바람, 물, 지열, 강수, 생물 유기체 등 재생 가능한 에너지를 변환시켜 이용하는 탄소 중립 에너지이다. 신재생 에너지는 화석연료의 고갈로 인한 에너지 자원 확보 및 에너지 공급 방식의 다양화뿐 아니라 기후 변화 협약 등 환경 규제에 대응하기 위해 필수적으로 필요한 에너지이다. 국내 신재생 에너지 누적 보급 용량은 2021년까지 총 30,212MW이고, 이 중 태양광 설비가 21,199MW로 가장 큰 70.2%의 비중을 보이고 있다[1]. 2022년에는 신재생 에너지 설비 용량이 전체 발전 설비 용량의 20%를 넘어서는 등 빠르게 설비 용량이 증가하고 있다[2]. 특히 태양광 발전은 친환경적이면서 지속 가능한 에너지원으로 각광받고 있으며, 향후에도 빠른 속도로 보급될 것으로 예상된다[3].
화력 에너지는 수요와 공급을 효율적으로 에너지를 관리할 수 있지만 무한한 에너지원을 가진 태양광 발전은 기상에 의존하기 때문에 발전량이 매우 간헐적이다. 따라서 태양광 발전량의 불확실성을 줄이고 경제성을 향상하기 위하여 정확한 발전량 예측 기술이 필요하다.
태양광 발전량 예측에 대한 장점은 다음과 같다.
첫째, 전력 수급 계획을 수립할 수 있어 안정적인 그리드 운영이 가능하며, 에너지 저장 장치(Energy storage system)의 스케쥴링을 최적화하여 에너지 낭비도 최소화할 수 있다.
둘째, 예측한 발전량과 실제 발전량의 비교를 통해 발전소의 성능 모니터링도 가능하다.
셋째, 태양광 발전소 설비의 안정적인 발전 설계, 수익 창출 및 이상 진단을 통한 새로운 비즈니스 모델을 창출할 수 있다[4][5].
본 연구는 2020년 1월부터 2023년 6월까지 수원과 목포 기상청에서 예보한 시간별 기상 데이터와 같은 기간 영암 및 연성 태양광 발전소의 시간별 발전량 데이터를 이용하여 단기 예측 모델을 제안하였다.
제안 예측 모델은 성능을 높이기 위해 입력 데이터의 특성을 늘리는 특성 공학(Feature engineering)을 이용하였다. 또한, 사이킷 런의 기계 학습 라이브러리인 선형회귀(Linear regression)를 통해 예측 성능이 가장 좋은 특성의 개수를 설정하였다. 마지막으로 다양한 딥러닝 모델을 사용하여 각 모델의 성능을 비교 평가하였다.
사용한 딥러닝 모델은 DNN, LSTM, BiLSTM, 1D-CNN, Multi kernel 1D-CNN이며, 각 모델을 병렬로 연결한 병렬 모델을 사용하였다. 병렬 모델은 DNN과 1D-CNN을 연결한 DCNN 모델, Multi kernel 1D-CNN을 연결한 DMCNN, LSTM을 연결한 DLSTM, BiLSTM을 연결한 DBiLSTM 모델을 사용하였다.
본 논문은 다음과 같이 구성되어 있다. 2장에서 관련 연구를 요약하고, 3장에서는 제안하는 모델 기반 방법에 대해서 설명한다. 4장에서는 실험 결과 및 분석을 제시하고, 5장에서 결론과 향후 연구 과제에 대해 논의한다.
Ⅱ. 태양광 발전 예측과 예측 모델
2.1 태양광 발전 예측
태양광 발전은 태양 에너지를 전기 에너지로 변환하는 시스템으로, 태양빛이 반도체 소자인 태양광 패널에 비추어지면, 전극 간에 전자가 이동하여 전기가 생성된다 태양광 발전은 태양 에너지로 전기를 생산하기 때문에, 일사량과 일조량이 매우 중요한 요소이며, 반도체 소자이기 때문에 적당한 온도를 유지해야 한다.
서론에서 서술한 바와 같이 태양광 발전은 기상 요소와 같은 자연 환경에 따른 발전량이 심하게 변하기 때문에 에너지를 효율적으로 관리하기 위해 정확한 발전량 예측이 필요하다. 이러한 발전량 예측을 위한 선행 연구는 다음과 같다,
H. Lee는 온도, 습도, 일사량 등 기상 데이터를 이용해 이동 평균(Moving average) 등으로 특성을 늘려 기계학습을 이용하였으며, 인공 신경망(ANN, Artificial Neural Network), 서포트 벡터 머신(SVM, Support Vector Machine), RBF(Radial Basis Function) 등 다양한 모델로 태양광 발전량을 예측하는 방법론을 제안하였다[6].
A. K. Yadav와 S. S. Chandel은 태양광 발전에 중요한 기상 요소인 일사량을 인공신경망(ANN) 모델로 예측하였다[7].
S. Lee와 W. J. Lee는 태양광 발전 시스템의 결함 검출을 위해 기후 데이터 및 태양광 발전량을 딥러닝 모델을 통해 예측 값과 실제 발전량을 비교하여 결함을 찾는 방법을 제안하였다[8].
B. C. Kim et al.은 시간별 태양광 발전량을 예측하기 위해 기상상태 및 과거 발전량을 사용하고 다양한 예측 모델을 개발하였으며, 이중 LSTM 모델의 정확도가 가장 우수한 것을 확인하였다[9]-[11].
C. B. Kim은 여름철 강수량을 예측하기 위해 다양한 딥러닝 모델을 병렬로 연결하여 시간당 강수량을 예측하였으며, 본 연구에서 DNN과 LSTM을 병렬로 연결한 모델이 가장 우수한 오차율을 보였다. 이러한 연구 결과들로 인해 최근에는 순환 신경망 구조를 지닌 LSTM 모델을 활용하여 시계열 데이터를 예측하는 연구가 부상하고 있다[12].
J. Zeng과 W. Qiao는 서포트 벡터 머신을 통해 단기 태양광 발전량을 예측하였다. 입력 데이터로는 2D 형태의 대기 투과율, 상대 습도 및 풍속을 포함한 기타 기상 변수를 사용하였고 출력 데이터는 예측된 대기 투과율을 현장의 위도와 시간에 따라 태양광 발전량으로 변환하였다[13].
표 1에 2020년 1월부터 2023년 6월까지 태양광발전량과 본 논문에서 사용한 기상요소 데이터의 상관관계에 대해서 나타냈다.
표 1에서 발전량과 기상 요소 중 일조량, 일사량, 습도는 상관관계가 높은 것을 알 수 있다. 그러나 일조 또는 일사량과 전운량은 상관관계가 높아야 하나 일조 후에는 발전량과 전운량은 전혀 관계가 없기 때문에 상관관계가 매우 낮게 나온 것을 알 수 있다.
2.2 특성 공학과 예측 모델
기계학습 모델은 지도학습으로 입력 요소와 타겟으로 데이터셋을 구성한다. 특히 입력 요소의 각 특성은 모델의 성능을 부가하는 중요한 요소이다. 특성 공학은 기존의 특성을 변형하거나 새로운 특성을 생성하는 것으로, 이동 평균과 같은 통계 기법으로 특성을 늘려 예측 모델의 성능을 높일 수 있다. 다음은 사이킷 런의 특성 변환기를 이용하여 2개의 특성을 6개의 특성으로 늘리는 예이다.
위 코드를 통해 2개의 특성(A, B)이 6개의 특성(1, A, B, A2, AB, B2)으로 변환된다. 즉, 길이, 두께, 높이 특성이 있다면, 이 세 가지 조합으로 새로운 체적 특성을 생성하여 모델의 성능을 향상하는 것이다. 이와 같이 모델 성능은 딥러닝 모델, 특성, 특성공학은 서로 밀접하게 연관되어 있기 때문에, 모델의 성능을 최대한 높이기 위해서는 이 세 요소를 잘 활용해야 한다, 특성 데이터로, 특성의 개수를 늘리면 훈련 셋에 대해 거의 완벽하게 학습을 할 수 있으나, 과적합이 발생하므로 이를 방지하기 위해 릿지 규제(Ridge regularization)를 사용하여 모델 향상을 도모한다. 릿지 규제는 모델의 과적합을 방지하기 위해 모델이 학습하는 동안 가중치에 제약을 주어, 너무 큰 가중치의 값을 억제하는데 목적이 있다. 이를 통해 모델이 데이터에 과도하게 맞추어져 예측 성능이 저하되는 현상을 방지할 수 있다. 릿지 규제에서 사용되는 손실 함수는 다음과 같다.
| (1) |
여기서 θj는 모델 가중치이며, λ는 규제 강도이다. 릿지 회귀의 핵심은 가중치의 크기에 패널티를 부과하여 너무 큰 가중치가 생기는 것을 방지하는 것이다. 규제 강도를 조절하여 모델의 복잡도를 조절할 수 있다.
딥러닝 모델은 기본적으로 DNN, 1D-CNN, Multi kernel 1D-CNN, LSTM, BiLSTM 등이 있다.
DNN은 입력 특성의 수치 패턴과 타겟 간의 관계를 학습하는 모델이다. 1D-CNN은 입력 특성의 수치 패턴과 타겟 간의 특징을 추출하는 컨벌루젼(Convolusion)과 특성 맵을 다운 샘플링하는 맥스 폴링(Max pooling)을 이용하는 모델이다. LSTM은 시계열 데이터에 우수한 성능을 보이는 모델이다. BiLSTM은 두 개의 LSTM 은닉층을 순방향과 역방향으로 연결하여 현재 시점의 데이터를 과거와 미래 데이터를 고려하여 처리할 수 있다. 이 때문에 다른 모델보다 시계열 데이터에 우수한 성능을 보이는 모델이다. 이번 연구도 시계열 데이터를 예측하는 실험이므로 기본 모델, 병렬 모델 중 가장 좋은 결과를 보일 것으로 예측된다.
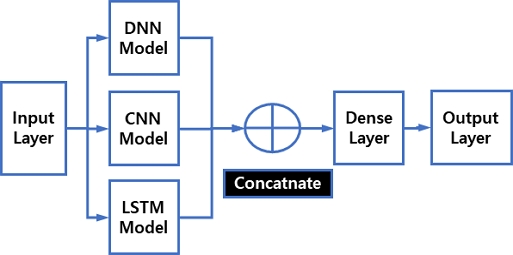
병렬 모델은 Keras API 함수로, 위에 기술한 기본 모델을 병렬로 구성한 모델이다. 병렬 모델은 각 기본모델로 중간층을 구성하고, 모델의 결과를 연결(Concatenate)하여 추가로 밀집(Dense) 모델을 연결한 모델이다. 그림 1에 병렬 모델에 대해서 나타냈다.
Ⅲ. 제안 딥러닝 예측 모델
본 연구는 사이킷 런(Scikit Learn)의 특성 변환기를 이용하여 degree를 2-5차원으로 조절하여, 기상 데이터의 특성을 다양하게 늘린 데이터를 사용하였다. 또한 사이킷 런의 기계학습 라이브러리인 선형회귀를 통해 예측 성능이 가장 좋은 특성의 개수를 설정하였다. 최종적으로 다양한 딥러닝 모델을 사용하여 예측 성능을 비교 평가하였다. 본 논문에서 사용한 딥러닝 모델은 DNN, LSTM, BiLSTM, 1D-CNN 등 기본 모델과 모델을 병렬로 연결한 병렬 모델을 사용하였다.
3.1 기본 딥러닝 모델
DNN 모델은 입력층은 기상 데이터 입력이다. 데이터 입력의 특성 수는 기상데이터 8개이며, 특성 변환기를 통해 degree 4로 특성을 늘린 494개이다. 중간층 6층, 중간층 노드 128 노드로 구성하였다. 출력층은 예측할 다음시간 전력량이다. LSTM과 BiLSTM은 시간 데이터로서 1일 24시간으로 타임스탬프 24개로 하였다. 또한, 입력층은 DNN과 동일하게 8개와 494개이다. 은닉층 노드 128개, 은닉층의 결과를 256 노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다.
1D-CNN 모델의 입력층은 DNN과 동일하게 8개와 494개이다. 또한, 합성곱 층으로 커널 수 256개, 커널 10, 스트라이드 1로서 256개의 특성 맵을 생성하였으며 맥스 풀링을 이용하였다. 풀링 결과는 커널 수와 동일한 256개의 스칼라 값이며, 이를 256 노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다.
Multi kernel 1D-CNN 모델의 입력층은 DNN과 동일하게 8개와 494개이다. 합성곱 층으로 필터 256개, 커널 10, 11, 12로 구성하였다. 따라서 3개의 커널을 거친 특성 값은 256개의 벡터가 3개로 구성되며, 맥스 풀링의 값은 768개의 스칼라 값이다. 이를 256 노드의 밀집 중간층과 32개의 밀집 중간층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다. 표 2와 3에 기본모델에 대해서 나타냈다.
3.2 병렬 딥러닝 모델
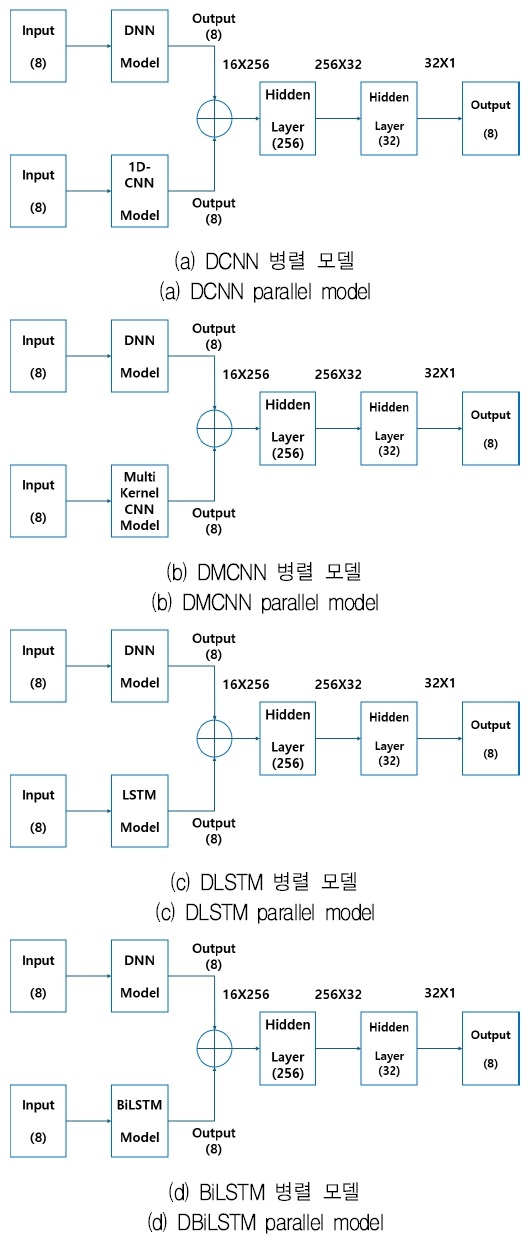
본 논문에서 병렬 모델은 DCNN, DMCNN, DLSTM, DBiLSTM 등 4개의 모델을 제안하였다.
DCNN, DMCNN 모델은 DNN 모델과 1D-CNN 및 Multi kernel 1D-CNN 모델을 병렬 연결한 모델이며, DLSTM, DBiLSTM 모델은 DNN 모델과 LSTM 및 BiLSTM 모델을 병렬 연결한 모델이다. 표 4에 병렬 모델에 대해서 나타냈다.
DCNN 모델은 표 2와 3의 DNN, 1D-CNN 모델의 출력을 8노드로 하여, 출력 결과를 연결한 16 노드에 대해서 256노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다.
DMCNN 모델은 표 2와 표 3의 DNN, MCNN 모델의 출력을 8노드로 하여, 출력 결과를 연결한 16 노드에 대해서 256노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다.
DLSTM 모델은 표 2의 DNN 모델과 LSTM 모델의 출력을 8노드로 하여, 출력 결과를 연결한 16노드에 대해서 256노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다.
DBiLSTM 모델은 표 2의 DNN 모델과 BiLSTM 모델의 출력을 8노드로 하여, 출력 결과를 연결한 16노드에 대해서 256노드의 밀집층과 32개의 밀집층으로 구성하였다. 출력층은 예측할 다음 시간 전력량이다. 그림 2에 병렬 모델에 대해서 나타냈다.
3.3 실험 데이터
본 연구는 2020년 1월부터 2023년 6월까지 목표와 수원 기상청에서 예보한 시간별 기상 데이터와 같은 기간 영암 및 연성 태양광 발전소의 시간별 발전량 데이터를 이용하였다.
기상 데이터는 기온, 강수량, 풍속, 습도, 운량, 일조, 일사량 등 7개의 기상요소를 이용하였다. 모델의 입력 데이터는 7개의 기상요소와 현재 시간의 전력량 등 8개이며, 타겟 데이터는 다음 시간의 전력량이다.
본 연구는 이러한 입력 요소를 사이킷 런의 특성 변환기를 이용하여 특성의 제곱, 각 특성의 곱으로 특성의 개수를 크게 늘려 훈련 셋에 대해 거의 완벽하게 학습하였다. 표 5에 특성 변환기를 이용하여 특성을 늘린 후 다중 선형회귀를 이용하여 결정계수(Coefficient of determination)로 평가한 것이다. 다음은 결정계수(R2)에 대해서 나타냈다.
| (2) |
표 5에서 degree가 4일 경우 학습 데이터와 테스트 데이터의 선형 회귀 결과 표준 점수가 가장 높은 것을 알 수 있다. degree가 5이상 되면 학습 데이터의 표준점수가 높아지나 테스트 데이터의 표준 점수가 낮아지는 전형적인 과적합 현상이 발생하는 것을 알 수 있다. 본 연구에서는 degree가 4일 경우의 데이터 셋을 이용하여 예측 모델의 성능을 평가하였다.
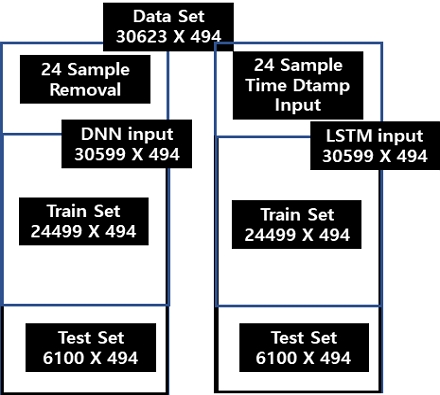
병렬 모델에서 DNN과 1D-CNN의 입력은 동일하나 LSTM 및 BiLSTM은 타임 스탬프 수만큼 입력 샘플을 삭제해야 한다. DNN과 1D-CNN의 총 데이터 셋은 30624개이며, 다음 시간 전력량 예측이기 때문에 모델에 사용한 샘플 수는 30623개이다. 학습 데이터와 테스트 데이터는 8:2로 분할하였다. 따라서 학습 데이터는 24499 개이고 테스트 데이터는 6124개이다. LSTM은 타임 스탬프 만큼 데이터 샘플이 제거되므로 총 샘플 수는 30599개이고, 학습 데이터는 24499 개이고 테스트 데이터는 6100개이다. 그림 3에 병렬 모델 입력에 대해서 나타냈다.
Ⅳ. 실험 및 성능 평가
본 실험은 Window10 환경에서 Anaconda, Python 3.6, Keras 2.6.0을 사용하였다,
모델의 하이퍼 파라메터는 학습 알고리즘으로 Adam을 사용하였으며, 학습률은 0.002, 배치 크기는 10로 하여, 100번 반복 학습하였다.
모델의 중간층 활성화 함수는 ReLU를 사용하였으며, 출력층 활성화 함수는 Linear를 사용하였다. 표 6에 실험에 사용한 하이퍼 파라메터에 대해서 나타냈다.
데이터는 각 독립변수의 크기가 다르기 때문에 데이터의 범위를 일치시켜야 한다. 또한, 딥러닝은 입력 데이터의 크기가 작아야 학습이 효과적이기 때문에, 0과 1 사이로 정규화(Normalize)하였다. 다음은 정규화 식에 대해서 나타냈다.
| (3) |
모델의 성능평가는 MAE(Mean Absolute Error), MSE(Mean Squared Error), RMSE(Root Mean Squared Error)를 사용하였다.
| (4) |
| (5) |
| (6) |
평균 절댓값 에러인 MAE는 절댓값을 취하기 때문에 가장 직관적이며, MSE는 제곱을 하기 때문에 특이 값에 민감하다. 또한 RMSE는 지표를 실제 값과 유사한 단위로 다시 변환한 값이다. MSE 보다 극단적 오차에 민감하며 데이터의 스케일에 따라 그 값을 직관적으로 이해할 수 있기 때문에 본 연구에서 모델의 성능을 비교할 때 가장 중심적으로 볼 것이다.
본 연구는 기본 실험, 특성 공학을 적용하지 않은 기본 모델 실험, 특성 공학을 적용한 기본 모델 실험, 특성 공학을 적용한 병렬 모델 실험 등 4개의 실험을 실시하였다. 실험은 10번 반복하여 평균을 나타냈으며, 각 결과에 대해 표준 편차를 나타냈다. 표 7에 기본 실험 결과인 선형회귀, 특성공학을 적용한 선형 회귀 그리고 릿지 규제를 적용한 선형 회귀에 대한 실험 결과를 나타냈다.
표 7에서 영암 발전소의 RMSE는 0.07925 이며, 연성 발전소의 RMSE는 0.07646 로서 특성 변환기의 degree가 4인 모델의 성능이 가장 좋은 것을 알 수 있다. 표 8에 특성공학을 적용하지 않은 기본 모델 실험 결과에 대해서 나타냈다.
표 8에서 연성 발전소와 영암 발전소가 모두 BiLSTM 모델의 성능이 가장 좋은 것을 알 수 있다. 영암 발전소의 RMSE는 0.0495 이며, 연성 발전소의 RMSE는 0.0495 로서 기본 실험 결과 오차율 보다 2배 가까이 오차가 줄어든 것을 확인 할 수 있다. 이것은 다른 연구에서 확인 한 바와 같이 시계열에 좋은 효과를 보이는 순환 신경망의 결과와 동일한 결과이다. 표 9에 특성공학을 적용한 기본 모델 실험 결과에 대해서 나타냈다.
표 9에서 표 8과 마찬가지로 BiLSTM 모델의 성능이 가장 좋은 것을 알 수 있다. 특성 공학을 적용하였을 때 전체적으로 RMSE 값이 감소하였으나 CNN 계열 모델에서는 값의 차이가 없거나 오히려 증가하는 현상이 발생했다. 영암 발전소의 RMSE는 0.0391 이며, 연성 발전소의 RMSE는 0.0368로서 특성을 늘리지 않은 데이터 셋의 오차율 보다 오차가 줄어든 것을 확인 할 수 있다. 이와 같이 기본 데이터 셋에 다양한 방식으로 특성을 늘림으로써 모델의 성능을 높일 수 있었다. 표 9에 본 논문에서 제안한 특성공학을 적용한 병렬 모델 실험 결과에 대해서 나타냈다.
표 10에서 연성 발전소와 영암 발전소가 모두 DNN과 BiLSTM을 연결한 DBiLSTM 모델의 성능이 가장 좋은 것을 알 수 있다. 기본 모델에서 가장 좋은 성능을 보인 BiLSTM 보다도 훨씬 뛰어난 성능을 보였다.
영암 발전소의 RMSE는 0.0326이며, 연성 발전소의 RMSE는 0.0231로서 본 논문에서 제안한 병렬 모델 중 가장 성능이 우수한 것을 알 수 있다. BiLSTM 모델이 DNN 모델의 시계열 데이터 학습 능력을 보완하고 DNN 모델이 BiLSTM 모델의 속도 및 단순성을 상호 보완해주는 역할을 하여 다른 병렬 모델에 비해 시계열 데이터 처리에 강점을 보였다.
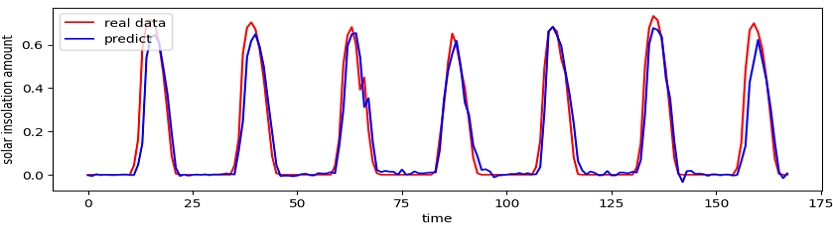
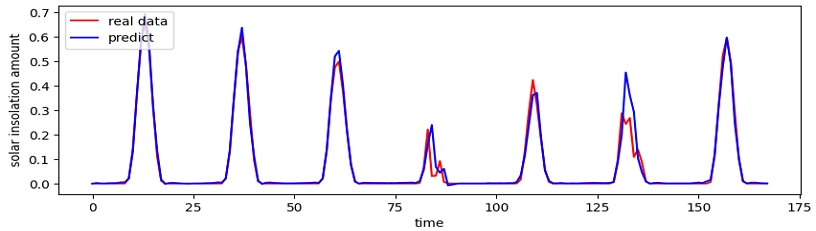
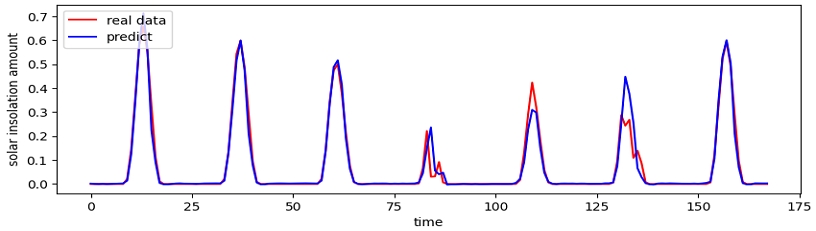
그림 4, 5는 기본 모델 실험 중 각각 영암 발전소와 연성 발전소 DNN 모델의 예측 결과를 그래프로 나타낸 것이다. 그림 6, 7은 병렬 모델 실험 중 각각 영암 발전소와 연성 발전소의 DBiLSTM 모델의 예측 결과를 그래프로 나타낸 것이다. 실험 결과 값이 가장 차이가 큰 두 모델을 비교함으로서 DBiLSTM 모델의 성능이 가장 우수한 것을 알 수 있다.
Ⅴ. 결론 및 향후 과제
본 연구는 특성 공학을 이용하여 입력 특성을 확장하고, 다양한 딥러닝 모델을 통해 태양광 발전량을 예측하였다. 실험은 기본 모델 실험, 특성 공학을 적용하지 않은 기본 모델 실험, 특성 공학을 적용한 기본 모델 실험, 특성 공학을 적용한 병렬 모델 실험 등 4개의 실험을 실시하였다. 실험 결과, 기본 모델에서는 특성 공학을 적용한 모델의 오차가 적었으며, 기본 모델 보다는 병렬 모델의 오차가 적었다. 특히, 병렬 모델인 DBiLSTM 모델이 영암 발전소의 RMSE는 0.0326 이며, 연성 발전소의 RMSE는 0.0231로서 본 논문에서 제안한 병렬 모델 중 가장 성능이 우수하였다.
병렬 모델은 기본 모델보다 중간층을 깊게 하지 않아도 우수한 예측률을 보였으며, 이것은 딥러닝의 문제점 중 기울기 사라짐(Vanishing gradient)에 의한 학습 저하 문제점을 해결할 수 있는 방안이다. Dnn 모델과 Cnn 모델은 각 시점의 입력 데이터에 대한 특성을 추출할 수 있는 장점이 있으며, LSTM과 BiLSTM은 시계열 데이터에 대한 특성을 추출할 수 있다. 특히 BiLSTM은 양방향으로 시계열 데이터의 특성을 추출할 수 있어 LSTM 특성을 확장한 것이라 할 수 있다. 따라서 이러한 모델들을 병렬로 연결함으로써, 각 단일 모델의 장점을 취할 수 있으며, 중간층을 깊게 하지 않고도 많은 학습 파라메터를 이용할 수 있어, 단일 모델보다 우수한 성능을 가질 수 있는 것으로 판단된다. 특히 DBiLSTM 모델은 DNN의 각 시점 데이터 특성 추출에 대한 장점과 시계열 데이터 특성 추출에 대한 장점으로 가장 우수한 모델이라는 것이 실험을 통해 증명되었다.
향후, 제안모델을 응용하여, 다양한 데이터에 대해서 보다 안정적이고 향상된 예측 딥러닝 모델에 관한 지속적인 연구를 진행할 예정이다.
References
- Status of Renewable Energy Deployment in Korea Electric Power Corporation (KEPCO), https://home.kepco.co.kr/kepco/SM/htmlView/SMCCHP00102.do?menuCd=FN29030301, [accessed : Jul. 28, 2024]
- Renewable Energy Statistics(Renewable Energy Center), https://www.knrec.or.kr/biz/pds/statistic/view.do?no=170, , [accessed : Jul. 28, 2024]
- W. B. Son, "Current status of solar power generation prediction technology in preparation for the expansion of renewable energy supply", Journal of The Korean Institute of Communications and Information Sciences, Vol. 40, No. 12, pp. 20-26, Nov. 2023.
- E. J. Lee, C. H. Min, and T. S. Kim, "Transformer-Based Photovoltaic Power Prediction Model Utilizing Multiple Weather Forecasts", The Institute of Electronics Engineers of Korea, Computer and Information, Vol. 45, No. 5, pp. 95-101, Sep. 2008.
-
T. K. Woo, M. S. So, S. Y. Kang, and J. H. Shin, "Development of a Solar Power Generation Prediction Model Utilizing Photovoltaics and Climate Data", Korean Journal of Computational Design and Engineering, Vol. 29, No. 1, pp. 33-41, Mar. 2024.
[https://doi.org/10.7315/CDE.2024.033]

-
H. Lee, "Use of the Moving Average of the Current Weather Data for the Solar Power Generation Amount Prediction", Journal of Korea Multimedia Society, Vol. 19, No. 8, pp. 1530-1537, 2016.
[https://doi.org/10.9717/kmms.2016.19.8.1530]

-
A. K. Yadav and S. S. Chandel, "Solar Radiation Prediction Using Artificial Neural Network Techniques : A Review", Renewable and Sustainable Energy Reviews, Vol. 33, pp. 772-781, May 2014.
[https://doi.org/10.1016/j.rser.2013.08.055]

-
S. Lee and W. J. Lee, "Development of a System for Predicting Photovoltaic Power Generation and Detecting Defects Using Machine Learning", KIPS Transactions on Computer and Communication Systems, Vol. 5, No. 10, pp. 353-360, Oct. 2016.
[https://doi.org/10.3745/KTCCS.2016.5.10.353]

-
B. C. Kim, et al., "Solar Power Generation Forecasting Based on LSTM Considering Weather Conditions", Journal of Korean Institute of Intelligent Systems, Vol. 30, No. 1, pp. 7-12, Feb. 2020.
[https://doi.org/10.5391/JKIIS.2020.30.1.7]

-
Y. Yu, J. Cao, and J. Zhu, "An LSTM Short-term Solar Irradiance Forecasting under Complicated Weather Conditions", IEEE Access, Vol. 7, pp. 145651-145666, Oct. 2019.
[https://doi.org/10.1109/ACCESS.2019.2946057]

-
A. Graves and J. Schmidhuber, "Framewise Phoneme Classification with Bidirectional LSTM and other Neural Network Architectures", Neural Networks, Vol. 18, No. 5-6, pp. 602-610, Jul. 2005.
[https://doi.org/10.1016/j.neunet.2005.06.042]

-
C. B. Kim, "Deep Learning Parallel Model for Improving Short-term Precipitation Prediction Using Meteorological Element Data", Journal of KIIT, Vol. 21, No. 10, pp. 47-57, Oct. 2023.
[https://doi.org/10.14801/jkiit.2023.21.10.47]

-
J. Zeng and W. Qiao, "Short-term solar power prediction using a support vector machine", Renewable Energy, Vol. 52, pp. 118-127, Apr. 2013.
[https://doi.org/10.1016/j.renene.2012.10.009]


2024년 8월 : 가천대학교 에너지 IT학과(공학사)
관심분야 : 머신러닝, 인공지능

1986년 2월 : 단국대학교 전자공학과(공학사)
1989년 2월 : 단국대학교 전자공학과(공학석사)
2009년 2월 : 인천대학교 컴퓨터공학과(공학박사)
1994년 ~ 현재 : 가천대학교 IT대학 컴퓨터공학과 교수
관심분야 : 사물인터넷, 딥러닝, 클라우드 컴퓨팅