산업응용에 적용되는 고정밀 이송용 SPMLSM 위치제어구현
초록
SPMLSM의 전류 제어기는 회전자 자속 기준 회전 좌표계에서 3상 전류를 d축과 q축 전류로 조정하여 정상 조건에서 d축과 q축에 PI 전류 제어기를 적용하여 정밀한 제어를 수행한다. 자기장과 추력에 대한 이론적 분석과 유한요소 결과 및 성능의 비교를 통해 모터 설계의 합리성을 검증하고, 시뮬레이션 결과의 정확성을 검증하기 위한 정적 힘 실험을 수행한다. 본 연구에서는 고정밀 이송장치에 적용되는 SPMLSM의 모델링을 하였고, 시스템 모델 방정식 및 제어방법을 설계하기 위한 드라이브 토폴로지에 대한 연구를 수행하였다. 시스템 구성을 통해 실시간으로 추정된 부하 토크는 1% 이내의 추정 오차를 가질 수 있어 이동 속도 제어기가 부하 변동에 적응하고 이동 속도를 추적하기 위한 안정적인 정상 상태에 도달함을 확인하였다.
Abstract
SPMLSM's current controller performs precise control by applying a PI current controller for the d-axis and q-axis in normal conditions by coordinating three-phase current into d-axis and q-axis current in the rotor magnetic flux reference rotation coordinate system. Through the theoretical analysis of magnetic field and thrust and the comparison of finite element results and performance, the rationality of the motor design is verified, as well as static force experiments to verify the accuracy of simulation results. In this study, the modeling of SPMLSM applied to high-precision transfer devices was carried out and a study on the drive topology was conducted to design the system model equation and control method. The load torque estimated in real time through the system configuration can have an estimation error within 1%, so it was confirmed that the moving speed controller adapts to the load fluctuations and reaches a stable normal state for tracking the moving speed.
Keywords:
SPMLSM, factory automation, position control, PI control, transfer machineⅠ. 서 론
18세기 중엽에 발명된 직선운동형 전동기는 초기에 섬유산업분야의 방적기 북(Flying Shuttle) 이송에 적용되어 활용되었다. 1946년 미국 웨스팅하우스에서 직선운동형 전동기를 이용하여 항공모함 상에서 비행기 이륙 보조장치인 캐터펄트(Aircraft catapult)에 적용한 이후, 다양한 활용분야로 활용범위가 확대되었다. 직선운동형 전동기의 학문적인 연구는 영국의 Laithwaite교수에 의해 1950년대부터 시작되었으며 최근 공장자동화(FA, Factory Automation) 및 로봇산업기술의 고도화와 응용장치의 확대에 따라 직선운동장치의 활용에 대한 산업수요가 크게 증가하고 있다[1]. 현재 직선운동형으로 구분되는 선형전동기는 초전도 자기부상 철도, 상전도 자기부상 철도, 철차륜식 선형 전동카, 직선형 엘리베이터 등의 수송기관, 반도체공정 이송기, 의공학 장치, 미소중력 시험장치, 비철금속 회수장치, 미분체 제조장치, 에너지 하베스트 BOS(Balance of System)를 비롯한 각종 시험장치 등 광범위한 응용장치에 적용되고 있다[2].
SPMLSM(Shaft-type Permanent Magnetic Linear Synchronous Motor)은 선형이송기 동작을 주목적으로 하는 샤프트형의 영구자석 선형동기전동기이다. SPMLSM의 경우는 회전형 동기전동기와 동일한 고정자와 회전자 형태를 가지고 있으며, 이러한 구조는 회전형 전동기를 방사방향 면으로 절단하여 이를 평면상에 펼쳐 놓은 구조로 회전자를 고정자, 고정자를 이동자로 간주하는 회전전기자형 구조를 갖는다[3]. FA산업의 활성화에 따라 자동화설비에서 고정밀 직선 왕복 운동을 필요로 하는 산업용 응용장치에서 높은 정밀도와 빠른 응답성능에 대한 요구가 부각되면서 리니어전동기를 적용한 직선 왕복 운동을 실현하는 선형전동기에 대한 수요가 증가하고 있다[4]. 선형전동기는 적용에 있어 체인 및 기어와 같은 추가적인 기계적 변환 장치 없이 샤프트를 따라 직선 운동이 이루어지므로 구조적으로 회전기에서 이용하는 볼-스크류(Ball-screw)방식이나 랙-피니언(Rack-pinion)방식의 선형이송기구와 다르게 소음이나 백래쉬(Back-lash)에 기인한 문제가 없으며 유지 보수가 용이하고 수명이 길다는 장점이 있다[5]. 특히 SPMLSM은 전기력으로부터 직접 추력을 발생시키기 때문에 다른 형태의 선형 운동기구보다 매우 높은 가속 성능을 얻을 수 있으며 제어방법에 따라 수㎛의 고정밀 위치제어가 가능하다는 특장점을 갖고 있다. 이러한 특징을 바탕으로 SPMLSM은 직선 운동에 의한 이동자의 선형이송동작이 요구되는 분야에 주로 활용되고 있다. 통상의 회전형 전동기의 경우에서는 전동기의 토크제어나 속도제어 성능이 주요한 성능요소로 평가된다는 점에 비하여 SPMLSM과 같은 선형전동기는 이동자의 위치제어 동작이 주요 성능요소로 평가되고 이에 대한 우수한 동특성이 요구된다[6]-[8].
FA분야에 적용되는 직선형 동력시스템으로서 선형전동기는 회전형전동기와 비교할 때 갖는 특장점으로 이동자와 고정자 사이가 공극에 의한 비접촉으로 소음과 마찰이 적다. 또한 다른 기계요소와 결합할 필요가 없는 기계적으로 가볍고 단순한 구조로 에너지 소비가 적다는 장점을 가지고 있다. 또한 빠른 가감속 특성을 가지고 있으며 에너지 전달 효율이 좋고 백래시(Backlash)가 없다[9]. FA분야에 샤프트리니어전동기의 적용은 고정밀 장비분야에서 주로 적용되고 있다. 정밀위치제어용으로 적용된 SPMLSM의 위치추적정밀도, 위치반복정밀도, 이동속도 및 발생추력 등의 주요 성능을 정확히 평가하는 것이 의미있는 요소가 된다. 따라서 본 연구에서는 SPMLSM의 모델링을 통해 시스템 모델방정식과 제어방법을 설계하기 위한 드라이브 토폴로지에 대한 연구를 수행하고자 하였고 고정밀 이송장치에 적용되는 SPMLSM의 모델링을 수행하고 시스템 모델방정식과 제어방법을 설계하기 위한 드라이브 토폴로지에 대한 연구를 수행하였다. 위치제어의 정밀도 향상을 위해 SPMLSM의 전류제어기는 회전자 자속 기준 회전 좌표계에서는 SVPWM기법을 적용하였다. 3상 전류가 좌표변환되어 직류전동기에서의 전류제어방법과 같이 d축과 q축에 대한 PI전류제어기 적용하여 정밀제어를 수행하였다. 시스템 구성을 통해 실시간 추정된 부하토크는 1% 이내의 오차범위에서 제어되고 이동속도제어기가 부하변동에 적응하며, 이동속도 제어가 안정적인 정상상태로 도달함을 확인할 수 있었다.
Ⅱ. SPMLSM의 이론고찰
2.1 SPMLSM의 구조와 동작원리
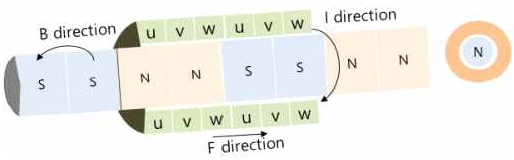
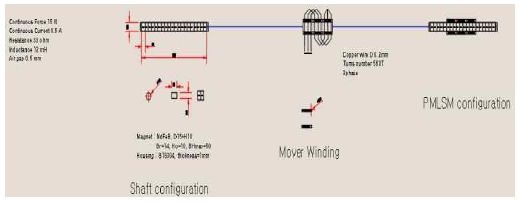
샤프트 타입의 PMLSM는 크게 코일 어셈블리(이동자)와 영구자석 어레이(고정자)로 이루어진다. 여기서, 코일 어셈블리는 절연체로 코일을 감싼 형태인 집중권 형태로 코일에 전류(I)가 흐른다. 영구자석 어레이는 희토류 강자성체로 N극과 S극을 마주하도록 구성하여 스텐레스 소재(STS304) 파이프 내부에 삽입하여 자기장(B)을 형성시킨다. 이러한 구조는 그림 1과 같다.
코일에 흐르는 전류와 자석의 자기장의 방향이 교차되면 로렌츠의 힘(Lorentz’s force, F)이 발생하여 이동자가 움직인다[10]. 이러한 원리를 통해 볼 때, SPMLSM은 회전형 전동기가 회전 운동력, 토크를 발생시키는 것과 비교할 때, 직선방향으로 작용하는 힘인 추력을 발생시킨다는 점에서 차이가 있지만 전기적인 구동원리는 로렌츠의 힘으로 표현되며 근원적으로 동일하다.
| (1) |
여기서, F는 추력, q는 입자의 전하량, E는 전기장의 세기, v는 속도, B는 자기장의 세기이다.
SPMLSM는 샤프트 상으로 강자성체를 N-S-S-N의 형태로 배열하여 고정자로 하며 샤프트의 외주에 코일을 배치하여 가동자로 한다. SPMLSM의 구조상 우수한 특징은 샤프트와 가동자가 비접촉형으로 되어 마찰열이 발생하지 않고 소음이나 먼지 발생이 거의 없다[11]. 이러한 구조적인 장점으로 인해 공극의 변동에 의한 추력의 영향이 거의 없으며 볼스크류를 활용한 기구 변경도 간단하다[12]. 또한 샤프트와 가동자의 흡착력이 없는 코어리스 형태이며 동작 중에 코깅현상이 없다. 외형상의 특징으로는 상대적으로 부피가 적고 기계적인 구조가 단순하여 주변 기기의 설계 및 부품 비용이 절감되며 선형규격에 의한 고정도의 위치 결정이 가능하다.
2.2 SPMLSM의 설계
SPMLSM은 샤프트 내에 강자성체를 N-S-S-N로 자석을 배열하여 고정자로 삼고 샤프트의 외주에 집중권 형태의 코일을 배치하여 가동자로 삼는다. 샤프트 전동기의 단면을 그림 2와 같이 샤프트 내에 배열된 자석의 자극으로부터 외부로 나오는 자속과 코일에 흐르는 전류에 의하여 플레밍의 왼손법칙에 의한 추력을 발생하는 구조이다[13]-[15].
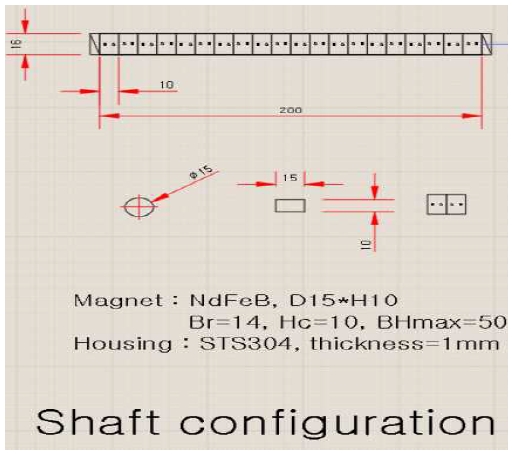
SPMLSM의 총 길이는 260[mm]로 제작되었으며 이동속도 측정과 위치정보의 획득을 위한 선형 엔코더를 활용한다. 설계에 따른 마그넷의 배열과 규격을 나타내며 NdFeB 자석에 직경이 15[mm], 높이가 10[mm], Br = 14, Hc = 10, BHmax = 50이며 마그넷의 배열은 NSSN으로 배열하여 자성이 상호 척력으로 작용하여 자력이 발생하도록 배열하였다.
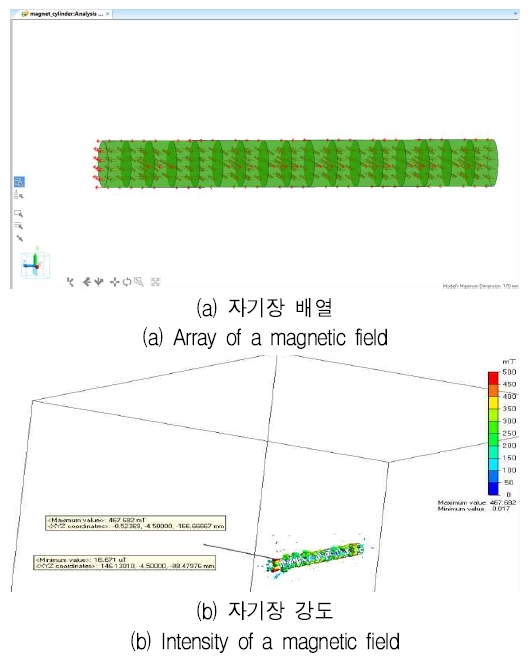
그림 3은 고정자 NdFeB 자석 배열에 따른 시뮬레이션 결과를 나타낸다. 자석의 배열과 자기장을 해석을 위한 시뮬레이션으로 자석 간의 경계면에서 자기장의 세기와 분포를 확인할 수 있다.
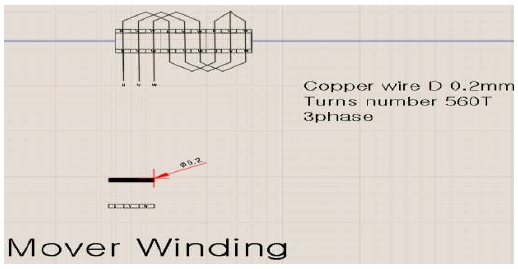
이동자 권선설계에서 권선의 직경은 0.202 mm로 AWG32에 해당하며 턴수는 560T, 한 상당 3개의 코일을 직렬로 결선한 집중권으로 Y결선으로 구성하였다. 그림 4에서는 이동자 권선구조를 나타낸다.
고정자와 이동자의 결합구조는 공극은 0.5mm이며 고정자의 하우징은 STS304소재를 적용하였다. 결합구조는 그림 5에 나타냈다.
이상의 설계 과정을 거쳐 나온 SPMLSM의 치수는 표 1과 같다.
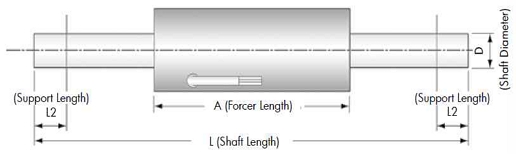
표 1에 나타낸 바와 같이 고정자의 극간 피치는 0.5[mm]이고 슬롯의 피치는 0.2[mm]로서 3극 6슬롯의 구조로 설계하였다. 일반 상온 및 대기 조건에서 물리적으로 이동자의 동작을 포함한 스토크스 가동길이를 측정하였다. 이동자를 초기 위치에서부터 최대 이동거리로 이동하여 목표위치를 설정하고 난 후 초기 위치에서 목표위치까지 좌우 이동을 반복한 상태에서 이동거리를 측정하였다. 스토크스 가동길이는 식 (2)와 같이 정의되며, 실제로 부하가 이동할 수 있는 거리를 의미하므로 어플리케이션의 적용에서는 스토크스 가동길이를 적용하여 시스템 설계에 활용하였다.
| (2) |
여기서, L은 샤프트 길이, L2는 양측 서포트 길이, A는 권선이 포함된 이동자의 길이를 의미한다.
그림 6은 SPMLSM의 외형에 따른 각부의 명칭을 나타낸다.
샤프트타입 리니어모터 유틸리티 결합 상태에서 정밀한 길이 측정장치를 이용하여 거리를 측정하여 실측한 데이터를 기반으로 가동범위를 산출하였다.
2.3 SPMLSM의 구동원리 및 모델링
SPMLSM의 전압방정식은 영구자석 선형동기전동기와 동일하게 표현되지만 두 전동기의 이동자의 구조가 다르기 때문에 그에 따른 쇄교자속 역시 다른 형태로 나타난다[16]. SPMLSM의 d-q축 쇄교자속식을 통해 전압방정식을 유도하고 전류에 대한 행렬식으로 정리하면 식 (3)과 같다.
| (3) |
여기서, 동기기준프레임에서 d축, q축에 대한 전류 iqs, ids와 인덕터 Lqs, Lds, 전압 Vqs, Vds, 고정자 저항 Rs, 각속도 ωs, 고정자 쇄교 자속 λPM을 의미한다. 추력식을 정리하면 식 (4)와 같다[12].
| (4) |
여기서, P는 극수, τ는 토크를 의미한다.
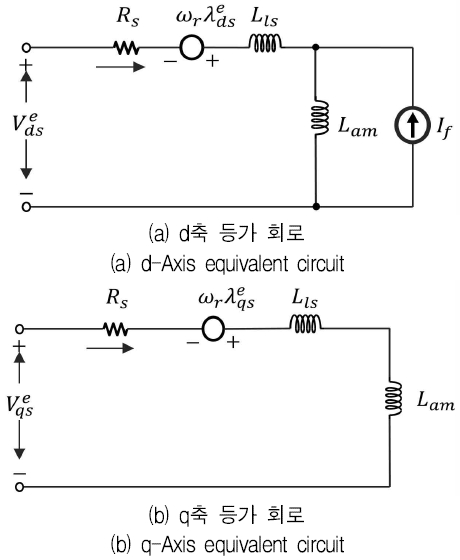
SPMLSM는 형태와 동작원리가 영구자석형 선형 동기전동기와 동일한 구조를 가지므로 그와 동일한 해석을 수행하였으며 단지 회전운동과 직선운동의 차이가 발생한다. 그림7은 동기 기준 프레임에서의 등가 회로를 나타낸다. 각각의 회로는 d축 및 q축에 해당하는 전압 방정식을 등가회로를 나타내었다. 등가회로에서 은 dq축 상의 자속과 각속도(위치)의 곱을 통해 이동자의 추력을 모델링하여 나타낸다.
샤프트형 영구자석 동기형 선형전동기에서는 고정자의 회로가 존재하지 않는 자석배열구조이기 때문에 고정자에 대한 전압방정식만을 구한다.
동기전동기의 고정자회로는 유도전동기와 동일하므로 고정자전압 방정식은 그림 7에서와 같이 등가회로해석을 통해 KVL을 적용하여 식 (5)와 같이 표현된다.
| (5) |
여기서, , , 로 나타낸다.
동기형 리니어전동기에서 회전자 권선의 쇄교자속 λabcs은 회전자 전류에 의해 발생한 자속성분 중에서 회전자 권선에 쇄교하는 자속 λabcs(s)와 영구자석에 의한 계자자속성분 중에서 회전자 권선에 쇄교하는 자속 λabcs(f)의 합으로 정의되며 식 (6)과 같다.
| (6) |
회전자 권선의 쇄교자속 λabcsf은 전류와 인덕턴스의 곱으로 나타낼 수 있고 영구자석에 의한 자속은 일정하게 나타나므로 이를 정전류원 형태의 계자전류 if에 의한 자속으로 등가화함으로서 λabcsf = Lfif로 나타낼 수 있다. 쇄교자속 λabcs을 계산하기 위해 필요한 인덕턴스를 함께 구해야 한다. 회전자 인덕턴스 Ls는 각각의 상권선에서 자기인덕턴스(Self inductance)와 상호인덕턴스(Mutual inductance)로 이루어지며 각 상권선의 자기 인덕턴스 Lasas, Lbsbs, Lcscs는 누설인덕턴스(Leakage inductance) Lls와 자화인덕턴스(Magnetizing inductance)로 구성된다.
회전형 동기전동기와는 다르게 샤프트타입 리니어전동기에서는 이동자의 위치변화에 따라 공극의 유효길이가 변화함에 따라 자기적인 돌극특성을 나타내고 자기인덕턴스의 크기 역시 변화한다. 일반적으로 샤프트타입 영구자석 리니어 동기전동기는 회전형 동기전동기와 동일하게 식 (7), (8)의 d-q축 고정자 전압방정식으로 나타낼 수 있다[2].
| (7) |
| (8) |
여기서, Vds는 d축 고정자 전압, Vqs는 q축 고정자 전압, Rs는 고정자 권선저항, ids는 d축 고정자 전류, iqs는 q축 고정자 전류, λds는 d축 고정자 자속쇄교, λqs는 q축 고정자 자속쇄교, ωe는 이동자의 각속도를 각각 의미한다. 이와 같이 전압방정식은 동기전동기와 동일하게 표현할 수 있지만 두 형태의 전동기의 이동자의 구조는 다르기 때문에 구조에 따른 쇄교자속은 다른 형태로 나타낸다. 식 (9)는 리니어 동기전동기의 d-q축 쇄교자속식을 나타낸다.
| (9) |
여기서, Lds는 고정자 d축 인덕턴스, Lqs는 고정자 q축 인덕턴스, λPM은 영구자석 자속쇄교이며 d-q에 대한 전압방정식을 다시 적으면 식 (10), 식 (11)과 같다.
| (10) |
| (11) |
위의 식 (10)과 (11)을 극수를 반영한 전류에 대한 식으로 다시 정리하면 식 (12), 식 (13)과 같다.
| (12) |
| (13) |
식 (12), (13)을 행렬로 나타내면 식 (3)과 같다.
샤프트타입 리니어전동기의 추력식을 정리하면 식 (4)와 같다.
샤프트타입 리니어전동기는 동작원리가 영구자석형 회전형 동기전동기와 동일한 구조를 가지므로 해석적 측면에서 동일한 해석을 수행할 수 있다.
2.4 고정밀 PI제어기 설계
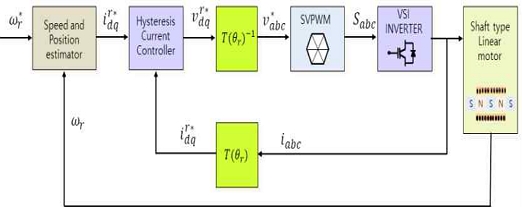
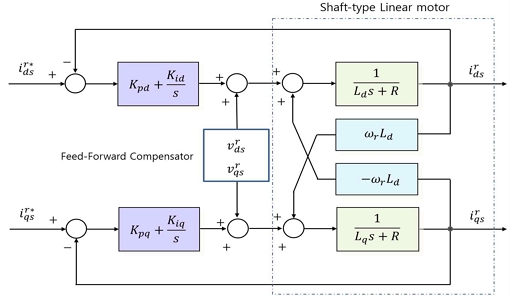
샤프트타입 리니어전동기의 전류제어기와 속도제어기의 설계를 통해 정밀위치제어가 이루어져야 한다. SPMLSM의 전류제어기는 회전자 자속 기준 회전 좌표계에서는 3상 전류가 d축 및 q축 전류로 좌표변환되어 정상상태에서는 직류 값을 가진다. abc-dq 좌표변환을 통해 3상동기전동기의 직류전동기의 제어방법으로 동일하게 구현하기 위한 방법이다[17]. 그림 8에서 는 직류값으로 속도레퍼런스가 입력되며 동기좌표계 상에서는 직류전류를 제어하게 되므로 직류전동기의 제어방식과 동일한 비례적분제어기(PI, Proportional Integration Controller)를 사용할 수 있다.
직류전동기에서 적용된 전류제어방식과 같이 d축 및 q축에 대한 PI전류제어기의 이득값을 식 (14)와 같이 나타낼 수 있으며[2] 이때, 영점과 극점이 상호 상쇄되어 전달함수는 1차 저역통과필터와 같이 설계할 수 있다.
| (14) |
d-q제어기에서는 계자자속에 의한 역기전력과 상호인덕턴스에 의한 자속 간섭성분은 고려해야 하고 이러한 요소들은 속도 기전력항으로 나타낼 수 있으며 이는 추가적인 전향보상항을 갖는다. 따라서 전기적인 모델과 PI전류제어기 모델을 포함한 샤프트타입 리니어전동기의 블록다이어그램은 그림 9와 같다.
Ⅲ. 시뮬레이션 및 실험
3.1 시뮬레이션
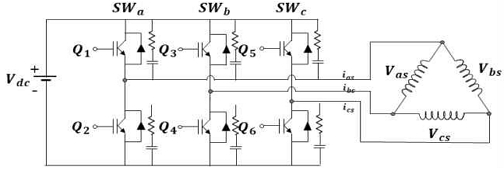
SPMLSM는 이동자의 위치를 검출하기 위한 리니어 엔코더를 필요로 하고 검출된 위치정보를 토대로 제어기를 통해 인버터 토폴로지 스위칭소자에 제어신호를 공급한다. SPMLSM의 인가전압은 SVPWM방식을 통해 인가전압을 생성하여 토폴로지에 공급한다. 그림 10은 3상 전압제어 인버터 토폴로지를 나타낸다.
공간고조파법을 이용하여 SPMLSM의 특성해석 프로그램을 완성하였는데, 일반적으로 집중회로정수법에서 나타낼 수 없는 전동기의 기계적 구조 및 배치에 대한 고려와 선형 기기의 특수성을 살펴볼 수 있는 해석 방법으로, 이를 설계 프로그램으로 확장하였다. 표 2는 시뮬레이션을 위한 파라미터를 나타내었다.
샤프트형 리니어전동기의 회전자 자속 기준 회전 좌표계에서는 3상 전류가 d축 및 q축 전류로 좌표변환되어 정상상태에서는 직류 값을 갖는다. 이것은 입력 및 출력을 나타낼 때 좌표변환을 수행하면 직류전동기의 제어방식과 상당부분이 동일하게 구현하기 위한 방법이다[4].
그림 11에서 는 직류값으로 속도레퍼런스가 입력된다. 동기좌표계 상에서는 직류전류를 제어하게 되므로 직류전동기의 제어방식과 동일한 PI제어기를 사용할 수 있다. 시뮬레이션을 위한 파리미터로 샘플링 주파수는 10k[Hz], 전원전압은 48[V], 전동기의 고유마찰상수는 100[μ]으로 설정하였다.
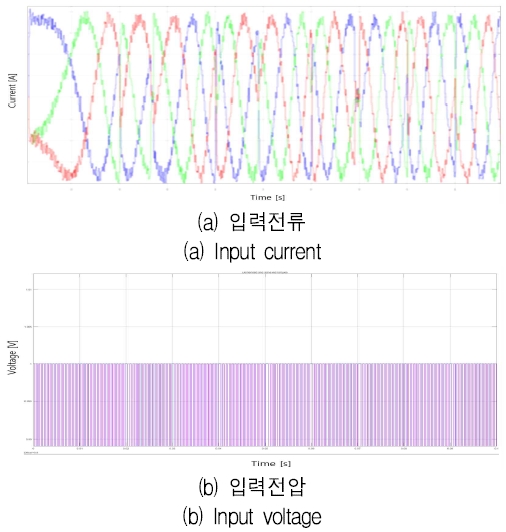
전압 벡터는 3개의 전압으로 공간 전압벡터 펄스폭 변조 방법에서 V1, V3, 그리고 V5를 인가하게 되며, 전압 펄스에 대한 전류의 응답을 통해 회전자의 위치를 검출하게 된다. 시뮬레이션을 통해 그림 12는 입력 전류 및 전압의 파형을 나타낸다.
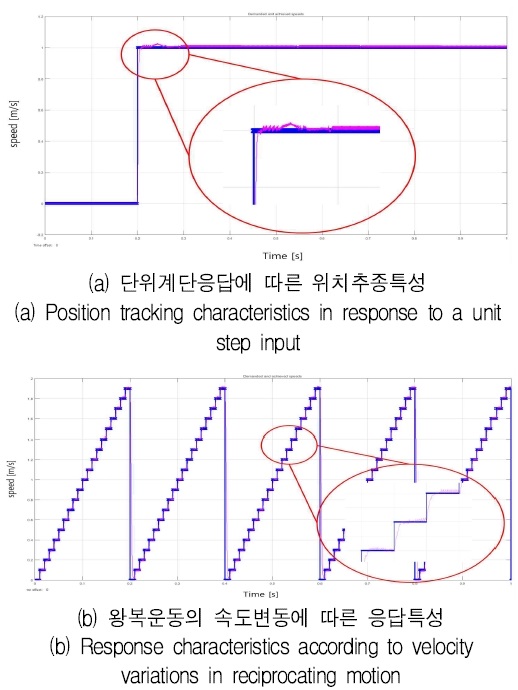
SPMLSM의 위치제어시스템의 기준 속도가 삼각파형으로 가변 될 때, 응답 특성을 분석하였다. 초기 저속의 지령 속도인 3[mm/s]에서도 제어 알고리즘이 정확하게 실제 속도와 위치를 추정하는 것을 통해 저속 영역에서의 위치제어 알고리즘의 성능을 확인할 수 있다. 0.2 초 이후에 지령 속도가 바뀌었을 때에도 실제 속도를 효과적으로 추정하는 것이 확인 가능하며 그림 13을 통해 확인할 수 있다.
3.2 위치제어 실험결과
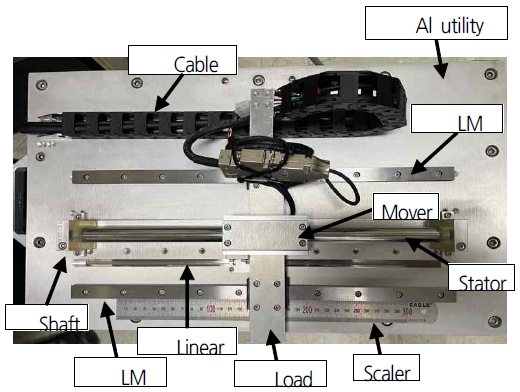
그림 14는 전체 시스템 유틸리티 구성 설계를 실제 구현한 사진이다.
제작된 SPMLSM 전동기는 그림과 같이 직선 운동을 할 수 있도록 LM가이드를 이용한 기구에 설치하였고 부하에 따른 가감속 특성을 시험하기 위하여 중량물 적재가 가능하도록 제작하였다.
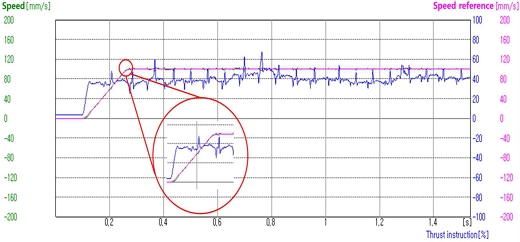
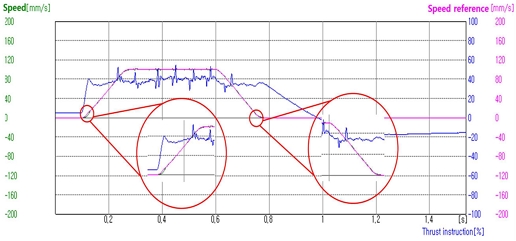
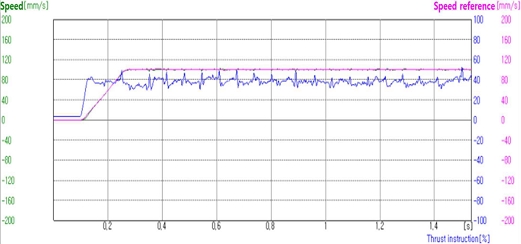
그림 15는 무부하에서 속도파형을 나타낸다. 속도 파형에서는 실제 이동자 속도[mm/s], 속도제어에 따른 레퍼런스 [mm/s], 추력값의 상대비율 [%]에 대한 변화를 나타내었다.
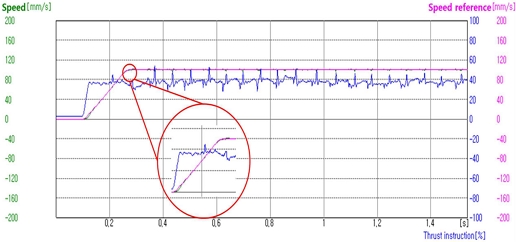
그림 16은 1N(0.98N) 부하조건에서 속도파형을 나타낸다. 1N의 이송부하를 적용하였을 경우의 속도제어 출력이 무부하속도제어 파형과 비교 할 때, 오차 범위 내에서 정밀하게 속도제어가 이루어짐을 확인 할 수 있다.
그림 17은 50mm 위치제어 출력파형을 나타낸다.
그림 18은 100mm 위치제어 출력파형을 나타낸다.
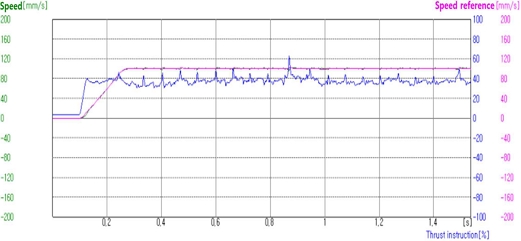
그림 19는 1N(0.98N) 부하조건에서 속도파형을 나타낸다.
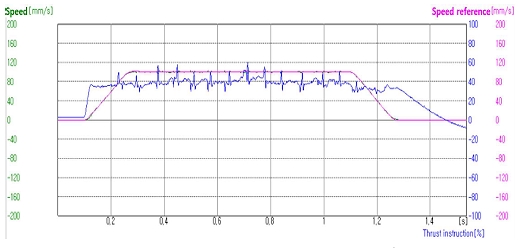
그림 20은 2N(1.96N) 부하조건에서 속도파형을 나타낸다.
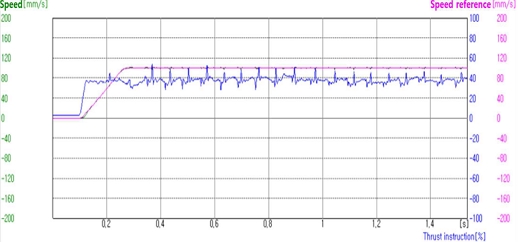
그림 21은 3N(2.94N) 부하조건에서 속도파형을 나타낸다.
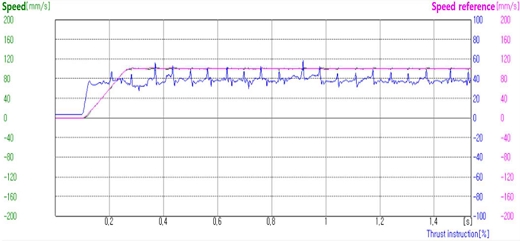
그림 22는 4N(3.92N) 부하조건에서 속도파형을 나타낸다.
그림 17과 그림 18을 통해 확인 바와 같이 50mm와 100mm의 위치결정제어서도 오차범위가 500us 이내로 매우 정밀한 위치제어가 이루어짐을 확인 할 수 있다. 실험결과 정밀도 1μm의 정밀도까지는 도달해 있으나 초정밀 가동을 위해서는 그 이하의 서브 마이크로미터까지의 위치 결정 정밀도를 유지할 수 있는 기구의 개발이 필요하다.
Ⅳ. 결 론
본 논문에서는 SPMLSM의 설계를 통해 샤프트 타입의 PMLSM을 설계 및 제작하여 FA에 적용되는 정밀위치제어용 전동기에 적용하였다. 또한, 고정밀 이송장치에 적용되는 SPMLSM의 모델링을 수행하고 시스템 모델방정식과 제어방법을 설계하기 위한 드라이브 토폴로지에 대한 연구를 수행하였다. 여기에 SPMLSM을 PI제어방식을 이용하여 공간벡터변조기법을 통해 제어신호를 발생시키고 위치정보검출에는 리니어 엔코더 기반으로 한 리니어모터의 위치제어에 대한 연구를 수행하였다. SPMLSM의 시변 계수들을 시불변 계수들로 변경하는 d-q변환을 통해 시변계수들을 제거하였다. 실시간 추정된 부하토크는 1% 이내의 추정오차를 가질 수 있어서 이동속도제어기가 부하변동에 적응하며, 이동속도 추종에 안정적인 정상상태로 도달함을 확인하였다. 향후에는 상태추정기의 수학적 모델의 정확도를 개선하여 시변파라메타에 대한 상태추정기를 구성하는 연구를 추가하여 고정밀 위치제어 시스템을 구현하도록 할 것이다.
Acknowledgments
이 논문은 2023년도 남부대학교 학술연구비의 지원을 받아 연구되었음.
본 과제(결과물)는 2024년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다(2021RIS-002)
References
-
B. Arundhati, S. K. Rao, and T. Kim, "High Performance of Linear Permanent Magnet Synchronous Motor Drive using Unscented Kalman Filter", International Journal of Control and Automation, Vol. 10, No. 11, pp. 223-232, Nov. 2017.
[https://doi.org/10.14257/ijca.2017.10.11.21]

-
P. G. Panah, M. Ataei, B. Mirzaeian, A. Kiyoumarsi, and A. Shafiei, "A Robust Adaptive Sliding Mode Control for PMLSM with Variable Velocity Profile Over Wide Range", Research Journal of Applied Sciences, Engineering and Technology, Vol. 10, No. 9, pp. 997-1006, Sep. 2015.
[https://doi.org/10.19026/rjaset.10.1866]

-
O. C. Kivanc and S. B. Ozturk, "MATLAB Function Based Approach to FOC of PMSM Drive", 2015 IEEE European Modelling Symposium, Madrid, Spain, pp. 96-102, Oct 2015.
[https://doi.org/10.1109/EMS.2015.81]

- J.-S. Kim, "Implementation of the High Performance Unified PID Position Controller for Linear Motor Drive with Easy Gain Ajustment", The Korean Institute of Electrical Engineers B, Vol. 51, No. 4, pp. 195-202, Apr. 2002.
-
G. Remy, J. Gomand, A. Tounzi, and P. Barre, "Analysis of the force ripples of a current loaded PMLSM", COMPEL - The international journal for computation and mathematics in electrical and electronic engineering, Vol. 28, No. 3, pp. 750-761, May 2009.
[https://doi.org/10.1108/03321640910941007]

-
Z. Zhang, L. Shi, K. Wang, and Y. Li, "Characteristics Investigation of Single-Sided Ironless PMLSM Based on Halbach Array for Medium-Speed Maglev Train", CES Transactions on Electrical Machines and Systems, Vol. 1, No. 3, pp. 375-382, Dec. 2017.
[https://doi.org/10.23919/TEMS.2017.8241359]

-
H. M. CheshmehBeigi and A.Khanmohamadian, "Comparison of Radial and Halbach Array PMLSM by Employing 2-D Electromagnetic Finite Element Analysis", Journal of Electrical and Computer Engineering Innovations, Vol. 4, No. 2, pp. 111-117, Nov. 2016.
[https://doi.org/10.22061/jecei.2016.571]

-
W.- Kim and B. C. Murphy, "Development of a Novel Direct-Drive Tubular Linear Brushless Permanent-Magnet Motor", International Journal of Control, Automation, and Systems, Salt Lake City, UT, USA, Vol. 2, No. 3, pp. 279-288, Sep. 2004.
[https://doi.org/10.1109/IAS.2003.1257779]

-
S. Ghazanfar and A. Deriszadeh, "Forecasting PMLSM Direct Thrust Control Based on Neural Network by Considering Motors Dynamic Behavior and Speed Effects", Majlesi Journal of Electrical Engineering, Vol. 4, No. 4, pp. 35-41, Dec. 2010.
[https://doi.org/10.1234/mjee.v4i4.300]

-
J. Gomand, G. Remy, A. Tounzi, P.-J. Barre, and J.-P. Hautie, "Impact of Permanent Magnet Field on Inductance Variation of a PMLSM", 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, pp. 1-9, Sep 2007.
[https://doi.org/10.1109/EPE.2007.4417589]

-
J. Kim, K. Cho, and S. Choi, "Lumped Disturbance Compensation using Extended Kalman Filter for Permanent Magnet Linear Motor System", International Journal of Control, Automation and Systems, Vol. 14, No. 5, pp. 1244-1253, Oct. 2016.
[https://doi.org/10.1007/s12555-014-0400-1]

-
H. Kim and Y.-W. Noh, "Study on Non-Singular Terminal Sliding Mode Speed Control and Vector Contro l f or Improving the Dynamic Respons e of Interior Permanent Magnet Synchronous Motor", The Transactions of the Korean Institute of Electrical Engineers, Vol. 72, No. 12, pp. 1646-1656, Dec. 2023.
[https://doi.org/10.5370/KIEE.2023.72.12.1646]

-
L. Yu, S. Chang, J. He, H. Sun, J. Huang, and H. Tian, "Electromagnetic Design and Analysis of Permanent Magnet Linear Synchronous Motor", Energies, Vol. 15, No. 15, pp. 5441, Jul. 2022.
[https://doi.org/10.3390/en15155441]

-
J.-I. Lee, Y.-C. Kim, J.-Y. Choi, and H.-W. Cho, "Analysis of Electromagnetic–Mechanical Characteristics according to Shaft Materials of Permanent Magnet Synchronous Motor", Energies, Vol. 15, No. 21, pp. 8046, Oct. 2022.
[https://doi.org/10.3390/en15218046]

-
X. Wang, F. Chen, R. Zhu, X. Huang, N. Sang, G. Yang, and C. Zhang, "A Review on Disturbance Analysis and Suppression for Permanent Magnet Linear Synchronous Motor", Actuators 2021, Vol. 10, No. 4, pp. 77, Apr. 2021.
[https://doi.org/10.3390/act10040077]

-
A. A. Tatevosyan, D. A. Polyakov, M. A. and Kholmov, "Characteristics Research of a Permanent Magnet Linear Synchronous Motor Driving Piston Compressor", 2021 3rd International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, Mar. 2021.
[https://doi.org/10.1109/REEPE51337.2021.9387980]

-
J.-H. Kim, J.-W. Choi, and S.-K. Sul, "High Precision Position Control of Linear Permanent Magnet Synchronous Motor for Surface Mount Device Placement System", PCC-Osaka 2002, Osaka, Japan, pp. 37-42, Apr. 2002.
[https://doi.org/10.1109/PCC.2002.998509]

- Y. C. Choi, "Sensorless Position Control of Shaft-type Linear Motor Using Extended Kalman Filter", Department of Electrical engineering, Graduate School of Nambu University, Dec. 2020.

1999년 8월 : 조선대학교 전기공학과(석사)
2006년 8월 : 동 대학원(박사)
2006년 8월 ~ 2009년 2월 : ㈜기영미다스 선임연구원
2009년 3월 ~ 현재 : 남부대학교 전기공학과 교수
관심분야 : control systems

2009년 2월 : 조선대학교 전기공학과(공학박사)
2015년 4월 ~ 현재 : 조선이공대학교 자동화시스템과 교수
관심분야 : IT융합, 신재생에너지