공간 가변적 커널 추정 및 적응적 밀도 맵 생성 기반의 해충 카운팅 모델
초록
해충의 조기 발견은 농작물 피해를 줄이고 생산성을 제고할 수 있는 중요한 작업이다. 이를 위해, 종래의 숙련된 농부가 육안으로 측정하는 방식을 탈피하여 디지털 트랩을 사용하여 포획된 해충 마릿수를 자동으로 측정하는 방제시스템이 도입되고 있다. 하지만, 포획된 해충의 폐색 문제로 인해 해충 카운팅의 정확도가 저하되고 있다. 이를 해결하고자 본 논문에서는 스택으로 쌓은 밀도 맵 기반 카운터와 커널 생성자로 구성된 해충 카운팅 모델을 제시하고자 한다. 특히, 커널 생성자를 통해 도트 맵을 밀도 맵으로 변환하기 위한 공간 가변적인 커널을 추정하고 카운터에서 적응적인 밀도 맵을 생성하는 딥러닝 아키텍처를 제안하고자 한다. 실험 결과를 통해, 제안한 스택 구조 기반의 커널 및 밀도 맵 생성 모델이 폐색이 존재하는 해충 이미지에서도 효과적이며 기존의 해충 카운팅 모델보다 평균 절대 오차에서 약 26%의 정확도를 개선할 수 있었다.
Abstract
Early detection of pests is an important task that can reduce crop damage and improve productivity. To this end, a control system is being introduced that automatically measures the number of captured pests using digital traps, breaking away from the conventional method of visual measurement by skilled farmers. However, the accuracy of pest counting is decreasing due to the problem of occlusion of captured pests. To solve this problem, this paper proposes a pest counting model consisting of a stacked density map-based counter and a kernel generator. In particular, we would like to propose a deep learning architecture that estimates spatially variable kernels for converting a dot map to a density map through a kernel generator and generates an adaptive density map from a counter. Through experimental results, the proposed stack structure-based kernel and density map generation model was effective even in pest images with occlusions and was able to improve accuracy by about 26% in mean absolute error compared to the existing pest counting model.
Keywords:
pest counting, stacked hourglass, crowd counting, density estimation, kernelⅠ. 서 론
무역화 및 기후변화에 따른 외래해충 및 돌발해충 유입이 증가하고 있으며 작물재배의 다양화 및 시설 재배의 증가로 인해 해충이 지속적으로 발생하고 있다. 이러한 해충은 농작물을 가해하여 품질 저하, 생산량 감소 및 경제적 손실을 초래한다. 따라서 해충 발생량을 조기에 신속·정확하게 파악하는 것이 농업 생산성 확보에 매우 중요하다. 이를 위해, 디지털 트랩을 노지에 설치하여 포획된 해충의 마릿수를 측정하는 방제시스템이 도입되고 있다. 디지털 트랩은 주광성 및 주화성 기반으로 해충을 유인하고 내장된 카메라를 사용하여 해충 이미지를 획득한다. 그리고 학습된 딥러닝 모델을 해충 이미지에 적용하여 최종 마릿수를 예측한다.
해충 이미지로부터 해충 마릿수를 계수하는 딥러닝 모델은 크게 객체 검출(Object detection)과 밀도 맵 추정(Density map estimation) 방식으로 나뉠 수 있다[1]. 객체 검출은 이미지에서 객체를 둘러싼 바운딩 박스를 검출하는 것에 목적을 두는 반면 밀도 맵 추정은 이미지에서 객체의 조밀한 정도를 표현한 밀도 맵을 생성하는 데 초점을 둔다. 객체 검출은 보행자, 자동차와 같이 객체의 크기가 적당하며 객체의 수가 수십 개에 불과할 때 효과적으로 동작한다. 하지만 해충 이미지와 같이 객체가 작으면서 해충 개수가 수백 마리에 이를 때 해충 간에 가려지는 현상, 즉 폐색 문제로 인해 검출 오류가 높아지게 된다. 따라서 밀도 맵 추정 방식이 해충 카운팅 모델의 대안으로 고려되고 있다.
해충 카운팅 모델은 기존의 군중 카운팅 모델에서 사용된 접근 방식을 채택하고 있다. 즉, 해충의 중심점을 흰색으로 표시한 도트 맵(Dot map)을 생성한 후, 가우시안 커널을 적용하여 밀도 맵을 생성한다. 그리고 해충 카운팅 모델을 학습하기 위해 생성된 밀도 맵을 실측값(Ground truth)으로 사용한다. 하지만, 기존의 해충 카운팅 모델은 해충의 폐색 문제로 인해 정확한 밀도 맵을 예측하는 데 어려움을 겪고 있다. 이러한 문제를 해결하기 위해, 본 연구에서는 밀도 맵 기반의 카운터(Counter)와 커널 생성자(Generator)를 각각 연속적으로 쌓은 스택 형태의 딥러닝 아키텍처를 새롭게 제안하고자 한다. 특히, 기존의 고정된 가우시안 커널 대신, 공간 가변적인 커널을 생성하고 스택 구조를 통해서 정확한 밀도 맵을 생성할 수 있는 해충 카운팅 모델을 소개하고자 한다. 실험 결과를 통해, 커널 생성자와 밀도 맵 카운터로 구성된 제안한 스택 구조가 해충 카운팅에 효과적이며 기존의 첨단 모델보다 정확도 측면에서 더 우수함을 확인하였다.
Ⅱ. 관련 연구
해충 이미지는 해충 수가 많다는 것과 해충 크기가 작다는 측면에서 군중 이미지와 아주 유사한 점이 있다. 이러한 이미지 특성에 착안하여, 현재 트랩에서 촬영된 해충 이미지에서 해충 마릿수를 계수하는 해충 카운팅 기술은 기존의 군중 카운팅 분야에서 개발된 접근 방식을 활용하고 있다. 원래 군중 카운팅 기술은 야외 공연장에 모인 수많은 인파를 계수하기 개발된 기술이다. 기존의 객체 검출과는 달리, 객체의 크기가 작은 스케일 문제와 객체 간 가려지는 폐색 문제가 주요한 걸림돌이 되고 있다. 이러한 문제를 해결하기 위해, 다중 스케일[2] 접근, 커널 및 밀도 맵 생성[3], 손실함수 모델링[4]에 기반한 다양한 군중 카운팅 기술이 개발되고 있다. 군중 카운팅 기술은 입력 이미지에서 추출된 특징 정보로부터 객체 수를 바로 예측하는 회귀(Regression) 방식에서 출발하여 현재는 밀도 맵을 추정하여 간접적으로 객체 수를 계산하는 방식으로 전환되고 있다. 대표적인 군중 카운팅 딥러닝 모델에는 MCNN[2], ICCNet[5], SANet[6], DM Counting[4], KDMG[3] 등이 있다.
밀도 맵 기반의 군중 카운팅 모델은 객체의 조밀한 정도를 표현하기 위한 밀도 맵을 생성한다. 일반적인 밀도 맵 생성 방식은 객체의 중심점을 흰색으로 표시하여 도트 맵을 생성한 후, 가우시안 필터링을 적용하여 밀도 맵으로 변환한다.
| (1) |
여기서 D는 도트 맵이며 kσ는 표준편차가 σ인 가우시안 커널이고 *는 합성곱 연산을 의미한다.
도트 맵은 이진 영상이므로 실제 식 (1)의 필터링 과정은 가우시안 커널을 도트 맵의 흰색 픽셀 위에 겹침으로써 쉽게 구현될 수 있다. 그리고 커널의 합은 1이기 때문에 밀도 맵의 픽셀의 합은 객체의 개수와 같도록 유지된다. 실측 밀도 맵이 주어진 경우, 딥러닝 모델을 학습하여 최종 밀도 맵을 추정할 수 있다. 그리고 밀도 맵의 픽셀 값을 합산하여 최종 객체 수를 결정한다.
Ⅲ. 제안한 공간 가변적 커널 추정 및 적응적 밀도 맵 생성 기반의 해충 카운팅 모델
3.1 제안한 접근 방법
기존의 Stacked Hourglass[7]를 활용하여 히트맵을 추정하는 아키텍처가 객체 검출 및 자세 추정에 효과적이라 검증되었다. 히트맵은 본 연구에서 다룰 밀도 맵과 아주 유사하다. 객체의 중심점을 사용하여 도트맵을 생성하고 가우시안 커널로 필터링하는 부분은 동일하다. 다만, 히트맵은 필터링 이후에도 커널의 중심점을 변경하지 않고 그대로 유지한다는 측면에서 차이가 있다. 따라서 본 연구에서는 밀도 맵의 정확도를 개선하기 위해, 기존의 Stacked Hourglass의 아키텍처를 활용한 해충 카운팅 모델을 개발하고자 한다. 또한 밀도 맵 추정을 위해 스택으로 쌓은 카운터(Counter) 외에, 공간 가변적으로 커널을 추정할 수 있는 커널 생성자(Generator)도 스택으로 쌓은 구조를 제안하고자 한다. 기존의 KDMG 모델[3]이 제안한 방법과 유사해 보이지만, Stacked Hourglass를 활용해서 스택으로 쌓은 구조가 아니다. 즉, 제안한 모델은 스택으로 쌓은 구조로 밀도 맵의 정확도를 개선할 수 있다는 점에서 기존의 KDMG와 큰 차이점이 있다. 또한 KDMG는 군중 카운팅에만 적용되었고 해충 카운팅 분야에 대한 효과성은 입증되지 않았다.
3.2 제안한 해충 카운팅 모델의 아키텍처
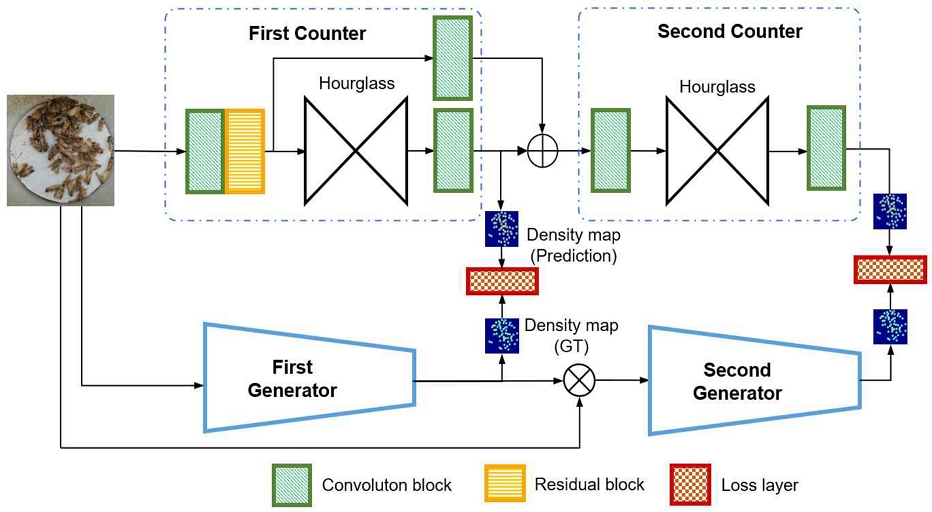
그림 1은 제안한 해충 카운팅 모델의 아키텍처이다. 그림에서 보듯이, 제안한 모델은 크게 카운터와 생성자로 구성되어 있으며 각각의 카운터와 생성자는 스택으로 쌓은 구조를 취하고 있다. 스택 구조에서 카운터와 생성자는 각각 Hourglass와 잘림(Truncated) VGG 모델[8]로 구현되었다. 여기서 카운터는 밀도 맵을 예측하는 역할을 담당하고 생성자는 공간적으로 변화하는 커널들을 추정하여 실측 밀도 맵을 생성하는 역할을 한다. 이는 제안한 모델에서는 고정된 가우시안 커널로 실측 밀도 맵을 만드는 것이 아니라 학습을 통해서 실측 밀도 맵을 생성한다는 것을 말한다.
그리고 첫 번째 커널 생성자에서 생성된 실측 밀도 맵을 개선하고자, 첫 번째 생성자의 결과인 실측 밀도 맵을 입력 해충 이미지와 곱하여, 즉 마스킹 처리하여 불필요한 정보를 제거한 후 두 번째 커널 생성자에 입력으로 넣어 최종 실측 밀도 맵을 생성한다. 그리고 각각의 카운터와 생성자에서 예측된 밀도 맵과 생성된 실측 밀도 맵의 오차를 계산한다. 즉, 첫 번째 카운터와 생성자에서 발생한 오차와 두 번째 카운터와 생성자에서 발생한 오차의 합을 최소화하기 위해 전체 모델을 학습한다.
3.3 커널 학습을 위한 생성자 모듈
커널 생성자는 입력 해충 이미지로부터 공간 영역에 따라 가변적인 커널을 추정한다. 속도 측면을 고려하여 픽셀 단위로 커널을 추정하지 않고 이미지의 가로와 세로 길이를 N등분하여 각 서브 영역별로 커널을 추정한다.
| (2) |
여기서 I는 입력 해충 이미지이고 Gf는 스택 구조에서 첫 번째 커널 생성자를 의미한다. 본 연구에서는 Gf를 위해 잘림 VGG 모델[8]을 사용하였다. VGG 모델의 4번째 컨볼루션 블록에서 자른 후, 컨볼루션 레이어를 추가하여 출력 형상의 크기를 결정하였다. 그리고 Kf는 추정된 커널로써, 3차원 배열이고 커널 형상은 (W/N) × (H/N) × k2이다. 여기서 W와H는 입력 해충 이미지의 가로 및 세로 길이에 해당한다.
| (3) |
여기서 Kf(j)는 j번째 픽셀에서 추청된 커널을 의미하고 1×1×k2 형상을 갖는다. Norm 함수는 커널 Kf(j)의 값이 양수이며 합이 1이 되도록 만든다. 본 연구에서는 Norm 함수를 위해 소프트맥스 함수를 적용하였다. Reshape 함수는 Kf(j) 형상을 k×k 크기의 2차원 배열로 변환한다.
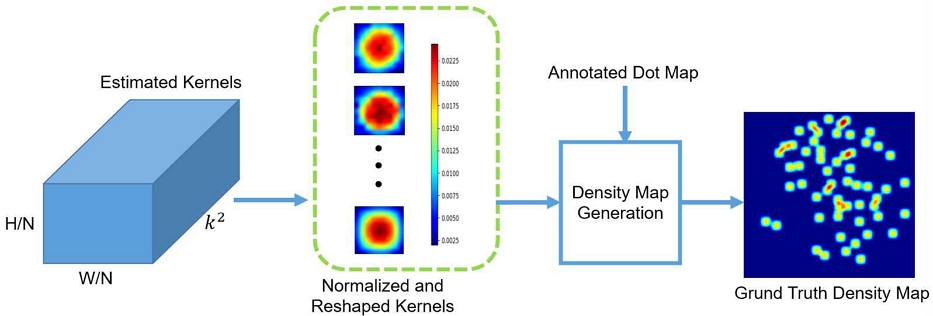
그림 2는 제안한 커널 생성자를 통해 추정된 커널 예시와 실측 밀도 맵 생성 과정을 보여주고 있다. 그림에서 보듯이, 커널 생성자는 3차원 커널을 생성한다. 그러나 커널 제약 조건을 만족하지 못하기 때문에 형상 변경과 정규화 과정을 통해 최종 커널로 변환한다. 커널 예시에서 보듯이, 예측된 커널이 가우시안 커널과는 다른 것을 알 수 있다. 그리고 추정된 각각의 커널들을 입력 도트 맵의 해당 좌표에 포개어 최종 실측 밀도 맵을 생성한다.
3.4 밀도 맵 예측을 위한 카운터 모듈
카운터 모듈은 커널 생성자 모듈에서 제공된 실측 밀도 맵을 예측한다.
| (4) |
여기서 Cf는 첫 번째 카운터 모듈인 Hourglass를 의미한다. 그리고 는 카운터에서 추정된 밀도 맵이고 생성자에서 제공된 실측 밀도 맵 Pf와 유사하도록 학습이 된다.
3.5 스택 구조 및 손실함수
제안한 아키텍처는 스택 구조이기 때문에 앞 절에서 소개한 생성자와 카운터 모듈을 한 번 더 수행한다. 먼저, 두 번째 생성자 모듈도 첫 번째 생성자와 내부 구조는 같다. 하지만 입력을 마스킹 처리된 값을 받는다.
| (5) |
이 식에서 Gs는 두 번째 생성자를 의미하고 ⊗는 원소별 곱을 의미한다. Pf는 해충의 밀집 정도를 반영하기 때문에 공간 어텐션 맵으로 간주할 수 있다. 따라서 I⊗Pf로 표현된 마스킹 처리는 입력 해충 이미지에서 중요한 정보는 남기고 불필요한 배경 잡음은 억제해 주는 역할을 한다.
두 번째 카운터 모듈도 첫 번째 카운터 모듈처럼생성자 모듈에서 제공된 실측 밀도 맵을 예측한다.
| (6) |
여기서 Cs는 두 번째 카운터 모듈인 Hourglass를 의미하고 첫 번째 카운터 모듈에서 추정된 밀도 맵인 를 입력으로 받아서 최종 밀도 맵 를 출력한다.
제안한 스택 구조에서의 최종 손실은 다음과 같다.
| (7) |
여기서 Lf와 Ls는 각각 첫 번째와 두 번째 생성자와 카운터 간의 오차를 나타낸다. 그리고 w는 각 손실에 대한 가중치이다.
| (8) |
| (9) |
본 연구에서는 실측 밀도 맵과 예측 밀도 맵 간의 오차를 ℓ2-놈(norm)을 사용하였다. 참고로 테스트 단계에서 최종 예측 밀도 맵은 두 번째 카운터의 예측치를 사용하기 때문에 w2를 w1보다 높게 설정하였다. 본 연구에서는 경험적인 방법을 통해 w2 = 0.8, w1 = 0.2로 설정하였다.
Ⅳ. 실험 및 결과
4.1 실험 환경
학습 데이터는 디지털 트랩에서 촬영된 해충 이미지 4,462장으로 구성되어 있으며, 7:3의 비율로 랜덤하게 훈련 집합과 테스트 집합으로 나누었다. 학습을 위해, Adam 최적화[9]를 사용했으며 배치 크기는 1, 에폭은 100회, 학습률은 1.25e-4로 설정했다. 모델 성능 평가를 위해, 밀도 맵 추정 방식기반의 군중 및 해충 카운팅 모델인 MCNN[2], SANet[6], ICCNet[5], KDMG[3], DM-Count[4], Stacked Hourglass[7], MaD2a- PCM[10]를 비교하였다.
4.2 정량적 평가
정량적 평가를 위해 군중 카운팅 분야에서 널리 사용되는 평균 절대 오차(MAE, Mean Absolute Error)와 평균 제곱근 오차(RMSE, Root Mean Squared Error)를 평가 척도로 사용했다. MAE는 측정된 해충 개수와 예측된 해충 개수와의 오차의 평균치로 해석할 수 있으며 반면 RMSE는 측정된 해충 개수와 예측된 해충 개수와의 오차의 제곱을 평균한 값으로 해석할 수 있다. MAE에 비해, RMSE는 해충이 많은 이미지에 대해 카운팅의 정확도를 더 정밀하게 진단할 수 있다.
| (10) |
| (11) |
여기서 n은 테스트 이미지 개수, 와 pi는 각각 모델이 예측한 해충 개수와 사람이 계측한 해충의 개수이다. 수식에서 보듯이, 두 지표 모두 수치가 작을수록 카운팅의 정확도가 높다. 그리고 를 계산하기 위해서는 추정된 밀도 맵의 픽셀 값을 모두 더해서 간접적으로 획득할 수 있다. 예를 들어, 제안한 모델의 경우, 식 (6)의 추정된 밀도 맵 의 픽셀 값을 모두 합산함으로써 최종 해충 개수를 산출할 수 있다.
표 1은 MAE와 RMSE 평가 결과를 보여준다. 표에서 보듯이, 제안한 모델이 기존의 밀도 맵 추정 기반의 카운팅 모델보다 정확도가 더 우수함을 볼 수 있다. 특히, 표에서 Stacked Hourglass[7]는 제안한 모델에서 생성자 부분을 제거한 모델을 말한다. 따라서 제안한 모델과 Stacked Hourglass 비교를 통해, 실측 밀도 맵을 생성하는 것이 기존의 고정된 가우시안 커널을 적용한 밀도 맵보다 더 효과적임을 알 수 있다. 그리고 표에서 KDMG[3]도 커널 생성을 통해 실측 밀도 맵을 생성하는 방식으로 기존 모델에 비해 성능이 우수한 편이다. 하지만 제안한 방법과는 달리, 스택으로 쌓은 구조가 아니기에 제안한 모델보다 정확도가 떨어지는 것을 볼 수 있다. DM-Count[4]는 최신 카운팅 모델중의 하나로써, 최적 전송(Optimal transport) 손실함수를 적용하여 밀도 맵을 추정하는 방식이다. 기존의 가우시안 커널을 사용하지 않고 도트 맵을 사용하여 카운팅을 예측하여 정확도를 상당히 개선한 것을 볼 수 있다. MaD2a-PCM[10]은 Stacked Hourglass 구조를 사용하며 Hourglass 간 어텐션 퓨전을 새롭게 적용하여 기존 모델 중에서 가장 우수한 성능을 달성한 것을 볼 수 있다. 하지만, 여전히 가우시안 커널을 적용한 밀도 맵을 사용하기에 제안한 모델보다 정확도가 떨어진다. DM-Count 모델의 결과에서도 유추할 수 있듯이, 실측 밀도 맵 생성 과정이 해충 카운팅의 정확도에 큰 영향을 미침을 알 수 있다.
4.3 밀도 맵 시각화
그림 3은 제안한 모델의 생성자와 카운터로 추정된 커널과 밀도 맵의 결과를 보여준다. 그림에서 제공된 밀도 맵은 제안한 모델의 두 번째 카운터에서 추출된 예측치에 해당한다. 이 추정된 밀도 맵을 합산하면 최종 해충 개수를 산출할 수 있다. 그림의 해충 이미지의 하단에는 육안으로 측정된 해충 개수가 있다. 그리고 예측 밀도 맵 하단에도 추정된 해충 개수가 있다. 그림에서 보듯이, 측정된 해충 개수와 예측된 해충 개수가 거의 비슷한 것을 볼 수 있다. 이는 제안한 스택 구조 형태의 실측 밀도 맵 생성 방법이 해충 카운팅의 정확도 개선에 아주 효과적임을 말해준다.
4.4 애블레이션 실험
첫째, 스택 구조에서의 카운터 위치에 따른 정확도를 평가하였다. 즉, 그림 1에서 첫 번째 카운터에서 추정된 예측 밀도 맵과 두 번째 카운터에서 추정된 예측 밀도 맵을 사용하여 MAE와 RMSE를 측정하였다. 표 2는 해당 결과로써, 첫 번째 카운터에서 출력된 밀도 맵이 두 번째 카운터에서 출력된 밀도 맵보다 정확도가 떨어지는 것을 볼 수 있다. 이는 제안한 스택 구조가 밀도 맵 추정에 더 효과적임을 말해준다.
둘째, 스택 구조에서의 마스킹 처리 전후의 정확도를 평가하였다. 제안한 모델에서는 첫 번째 생성기의 실측 밀도 맵을 입력 해충 이미지와 곱하여 마스킹 연산을 적용한다. 이는 불필요한 정보를 제거하여 관심 영역에 더 집중할 수 있는 효과를 거둘 수 있다. 이를 검증하기 위해, 마스킹 전후의 MAE와 RMSE를 평가하였고 표 3에서 보듯이 제안한 스택 구조에서의 마스킹 연산이 효과가 있음을 확인하였다.
Ⅴ. 결 론
본 논문에서는 기존의 고정된 가우시안 커널을 사용하여 밀도 맵을 생성하는 방법이 아닌, 학습을 통해 커널을 생성하는 밀도 맵 생성 기반의 해충 카운팅 모델을 제안하였다. 특히 밀도 맵의 정확도를 개선하고자 스택 구조의 생성자와 카운터로 구성된 아키텍처를 새롭게 제안하였다. 그리고 스택 구조를 활용하기 위해, 첫 번째 생성자의 출력 값인 실측 밀도 맵을 공간 어텐션으로 활용하여 두 번째 생성자의 성능을 개선하였다. 실험 결과를 통해, 제안한 생성자 및 카운팅 기반의 해충 카운팅 모델이 기존의 Stacked Hourlgass 모델보다 더 우수한 성능을 달성하였다. 이를 통해 커널 생성자가 해충 카운팅에 효과적임을 검증하였다. 또한 스택 구조에서의 카운터 위치와 마스킹 적용 여부에 따른 실험을 통해, 제안한 스택 구조에서의 마스킹 연산이 공간 어텐션의 역할을 수행하며 예측 밀도 맵 추정에 도움을 준다는 가설을 검증하였다.
제안한 해충 카운팅 모델은 웹 애플리케이션으로 구현되어 노지에 설치된 트랩에서 촬영된 이미지에 적용되어 해충 카운팅 서비스를 제공하고 방제시스템과 연계될 예정이다. 이를 통해, 시즌별 방제 효과를 높여 농가의 생산량과 품질을 제고할 것으로 기대된다.
Acknowledgments
본 성과물은 농촌진흥청 연구사업(과제번호: PJ01630303)의 지원에 의해 이루어진 것임
References
-
J.-H. Lee and C.-H. Son, "Trap-based pest counting : Multiscale and deformable attention CenterNet integrating internal LR and HR joint feature learning", Remote Sensing, Vol. 15, No. 15, pp. 3810, Jul. 2023.
[https://doi.org/10.3390/rs15153810]

-
Y. Zhang, D. Zhou, S. Chen, S. Gao, and Y. Ma, "Single-image crowd counting via multi-column convolutional neural network", in Proc. IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 589-597, Jun. 2016.
[https://doi.org/10.1109/cvpr.2016.70]

-
J. Wan, Q. Wang, and A. B. Chan, "Kernel-based density map generation for dense object counting", IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 44, No. 3, pp. 1357-1370, Mar. 2022.
[https://doi.org/10.1109/tpami.2020.3022878]

- B. Wang, H. Liu, D. Samaras, and M. Hoai, "Distribution matching for crowd counting", in Proc. Neural Information Processing Systems, Vancouver, Canada, pp. 1595-1607, Dec. 2020.
- V. Ranjan, H. Le, and M. Hoai, "Iterative crowd counting", in Proc. European Conference on Computer Vision, Munich, Germany, pp. 278-293, Oct. 2018.
-
X. Cao, Z. Wang, Y. Zhao, and F. Su, "Scale aggregation network for accurate and efficient crowd counting", in Proc. European Conference on Computer Vision, Munich, Germany, pp. 757-773, Oct. 2018.
[https://doi.org/10.1007/978-3-030-01228-1_45]

-
A. Newell, K. Yang, and J. Deng, "Stacked hourglass networks for human pose estimation", in Proc. European Conference on Computer Vision, Amsterdam, Netherlands, pp. 483-499, Sep. 2016.
[https://doi.org/10.1007/978-3-319-46484-8_29]

-
K. Simonyan and A. Zisserman, "Very deep convolution networks for large-scale image recognition", In Proc. International Conference on Learning Representation, May 2015.
[https://doi.org/10.48550/arXiv.1409.1556]

-
D. P. Kingma and J. Ba, "Adam: A method for stochastic optimzation", In Proc. International Conference on Learning Representation, San Diego, USA, May 2015.
[https://doi.org/10.48550/arXiv.1412.6980]

-
W.-D. Lee, C.-H. Son, and S.-W. Park, "Multiscale and deformable density attention model for trap-based pest counting", Journal of Korean Institute of Information Technology, Vol. 21, No. 12, pp. 1-11, Dec. 2023.
[https://doi.org/10.14801/jkiit.2023.21.12.1]


2017년 4월 ~ 현재 : 군산대학교 컴퓨터소프트웨어학부 부교수
관심분야 : 컴퓨터 비전, 영상처리, 기계학습, 딥 러닝

2020년 3월 ~ 현재 : 군산대학교 컴퓨터소프트웨어학부 학사과정
관심분야 : 컴퓨터 비전, 영상처리, 기계학습, 딥 러닝