주파수 영역 저역 필터에 의한 위상 변환 일반 상호 상관 시간 지연 추정기 성능 개선

Ⅰ. 서 론

두 개 이상의 센서 간의 시간 지연 차이 추정은 신호원의 수동적 위치 파악을 위한 중요한 방법이다[1]. 이는 소나[1], 레이더[2][3], 실내 측위[4]-[6], 위성통신[7], 음향영상[8], 배관 손상측정[9] 또는 지진학 시스템[10] 등 많은 분야에서 중요한 역할을 한다. 상호 상관 (Cross correlation) 방법은 수신기가 수신한 신호 간의 상호 상관관계를 기반으로 하는 시간 지연 추정법으로 유용한 방법으로 여겨져 왔다. 또한 많은 연구자가 상호 상관법을 수정한 방법들을 제안하였다. 그중에 Carter 등에 의해서 제안되고 후속 연구로부터 성능이 향상된 일반화된 상호 상관 (GCC, Generalized Cross Correlation)에 의한 시간 지연 추정법이 있다[1][11][12]. GCC를 사용한 시간 지연 추정을 위해서 GCC-ML(Maximum Likelihood), GCC-Roth(Roth), GCC-PHAT(Phase Transform) 등과 같은 다양한 주파수 영역에서 가중치 함수를 설계하였고, 이 중에 GCC-PHAT가 여러 응용에 시간 지연 추정 방법으로 광범위하게 적용되고 있다[13]-[15]. 이 GCC-PHAT는 여러 후속 연구를 통해서 공간적 정보와 희소 정보[16][17]를 사용하거나, TDE와 채널 추정을 결합하거나[18][19] 또는 사전 정보[5][20]를 이용하는 등의 방법으로 GCC의 추정 성능을 향상시키는 시도가 있었다. 이런 GCC 성능 향상 연구 중에도 참고문헌[21]과 [22]는 GCC-PHAT의 연산 과정 중 마지막 과정인 IDFT의 결과가 하나의 임펄스성 신호로 나온다는 것에 착안하여 IDFT 이전을 하나의 주파수를 갖는 신호가 존재하는 시간 영역으로 생각하고, IDFT 이후를 그 주파수를 추정하는 주파수 영역으로 생각하였다. 참고문헌[21]은 IDFT 이전의 신호에서 잡음에 섞인 단일 주파수 성분 신호가 가진 주기성을 이용하여 자기 상관을 함으로써 주기성 있는 원하는 신호와 주기성이 없는 잡음 사이의 분리를 시도하였고, 참고문헌[22]은 SSA(Single Spectrum Analysis) 기법을 이용하여 참고문헌[21]의 성능을 좀 더 향상시켰다. 이런 GCC 알고리즘 자체에 관한 연구와 아울러 GCC와 연관하여 딥러닝을 이용한 시간 지연 추정 결과도 최근 연구에서 살펴볼 수 있다[23][24]. 이 논문을 살펴보면 조금씩 변형된 백색화 과정을 사용하는 GCC들의 결과들을 종합하여 더 좋은 결과를 선정하는데 딥러닝을 사용하거나[23], 딥러닝 방법으로 GCC에 입력되는 신호 자체를 denoise하는 접근을 한 결과들을 소개하고 있다[24].

본 논문에서는 참고문헌 [21][22]와 같은 관점에서 출발하여 GCC-PHAT 연산 과정을 DFT로 다시 해석하는 과정에서 시간 지연 추정에 실제로 사용되는 필요 주파수 대역이 있음을 파악하고, 이 필요 대역을 저역 통과 필터를 통해서 분리한 후 GCC-PHAT의 최종 단계를 실시하게 함으로써 시간 지연 추정에 불필요한 잡음 성분이 개입되는 것을 배제할 수 있고, 이를 통해서 GCC-PHAT로 추정한 시간 지연 추정의 평균 자승 오차값을 개선할 수 있음을 보인다. 이 결과를 보이기 위해서 –10dB ~ 10dB 사이의 신호 대 잡음 비에서 모의실험을 하고, 참값을 기준으로 한 평균 자승 오차를 구한다. 이때 다양한 차단 주파수를 갖는 저역 통과 필터를 적용한 결과들을 서로 비교한 결과를 도출한다. 도출된 결과를 분석하여 저역 통과 필터를 적용하는 것이 중저 수준 신호 대 잡음 비에서 평균 자승 오차 수준을 낮출 수 있음을 보인다.

본 논문의 구성은 2장에서 GCC-PHAT의 기본 구조를 설명하고, 이 구조에 저역 통과 필터를 사용하여 성능을 향상시킬 수 있음을 GCC-PHAT의 재해석을 통해 보인다. 3장에서는 모의실험을 통해서 2장의 결과를 확인하고 4장에서 결론을 맺는다.

Ⅱ. 저역 통과 필터를 사용한 상호 상관 기반 시간 지연 신호 추정 기법

2.2 저역 통과 필터를 사용한 GCC-PHAT 기반 시간 지연 추정 방법

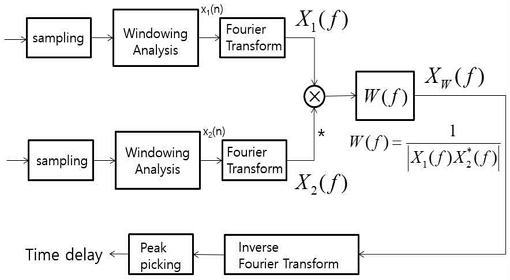
GCC-PHAT는 일종의 백색화 가중치를 사용하는 상호 상관 추정 기법이다. 주파수 영역에서 두 수신기 신호 간의 곱을 구한 후에 백색화 가중치 과정을 통과시켜서 위상만을 남김으로써 신호의 스펙트럼 크기의 영향을 배제한다. 전통적인 GCC-PHAT 기반의 시간 지연 추정 과정을 그림1에 나타내었다. 그림 1의 GCC-PHAT 방법을 간략히 기술하면 다음과 같다. $$ {\mathit{r}}_{\mathit{s}}\in {\mathit{R}}^3$$에 위치한 신호원에서 $$ {\mathit{r}}_1,{\mathit{r}}_2\in {\mathit{R}}^3$$에 위치한 두 수신기가 각각 도래하는 신호에 시스템에서 원하는 최소 시간 지연량을 만족하는 표본화 속도를 선택하여 아날로그 신호를 표본화한 후에, 원하는 주파수 분해능을 보장하는 시간 길이 만큼씩 해닝 창함수와 같은 창함수를 이용하여 프레임을 만든다. 각각의 신호를 푸리에 변환한 후 가중함수 W(f)를 이용하여 위상만을 남겨서 시간 지연 정보만을 얻은 후 역 푸리에 변환하여 최종 상호 상관 함수를 구하고 위상에 포함된 시간 지연에 해당하는 위치에서 최대치를 만드는 결과를 얻는다.

Fig. 1.

Diagram of GCC-PHAT

그림 1에서 프레이밍을 끝낸 각 채널의 데이터열인 x₁(n)과 x₂(n)을 이용하여 그림 1의 흐름을 따라 각각을 DFT(Discrete Fourier Transform)를 하면 아래 식과 같다.

$\[ X_1\left(f\right)=\sum _{n=0}^{N-1}{x}_1\left(n\right)e^{-j\frac{2\pi fn}{N}} \]$

(2-a)

$\[ X_2\left(f\right)=\sum _{n=0}^{N-1}{x}_1\left(n-\tau \right)e^{-j\frac{2\pi fn}{N}}=e^{-j\frac{2\pi f\tau }{N}}{X}_1\left(f\right) \]$

(2-b)

위 두 신호 중 X₂(f)의 공액복소수와 X₁(f)를 곱한 후 그에 백색화 가중치로 나누어 X_W(f)를 구하면 다음과 같이 시간 지연량만 존재하는 위상만이 남는다.

$\[ X_W\left(f\right)=e^{j2\pi f\tau } \]$

(3)

위 식을 그림 1의 마지막 단계에서 IDFT(Inverse Discrete Fourier Transform)을 이용하여 상호 상관 식을 구하면 다음 식과 같다.

$\[ R_{x_1{x}_2}\left[n\right]=\frac{1}{N}\sum _{f=0}^{N-1}{e}^{\frac{j2\pi f\tau }{N}}{e}^{\frac{j2\pi fn}{N}}=\delta \left(n+\tau \right) \]$

(4)

즉 n = -τ에서 상관도에 최고치가 생긴다.

만약 f 변수를 시간 변수로 삼고 변수 n을 주파수 변수라고 생각하여 X_W(f)에 대해서 IDFT가 아닌 DFT를 이용한다면,

$\[ R_{x_1{x}_2}\left[n\right]=\sum _{f=0}^{N-1}{e}^{\frac{j2\pi f\tau }{N}}{e}^{-\frac{j2\pi fn}{N}}=N\delta \left(n-\tau \right) \]$

(5)

가 된다. 즉 n = -τ에서 상관도에 최고치가 생긴다. 시간 지연 추정을 위해서 시간 정보만 본다면, 이는 IDFT를 사용한 결과가 시간상으로 미러링 된 결과가 된다. 즉 절대 시간 지연량은 같고 부호만 바뀌는 결과를 얻는다. 따라서 미리 시간상으로 미러링이 된다는 사실을 염두에 둔다면, X_W(f)에서 f 변수를 시간 변수로 삼고 R_x1x2(n)에서 변수 n을 주파수 변수라고 생각하여 IDFT대신 DFT를 사용해도 시간 정보를 얻는 것에는 문제가 없다고 된다고 할 수 있다.

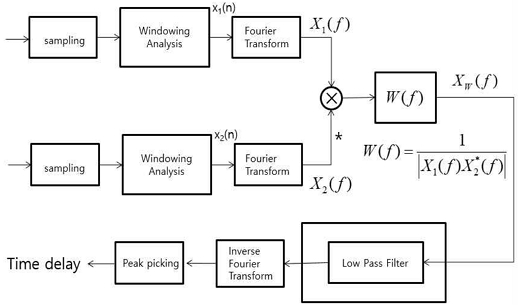
그리고 두 수신기 간 이격에 의한 최대 시간 지연이 τ_max 샘플 스텝이라고 할 때, 최대 지연 값 τ_max에 해당하는 주파수는 2πτ_max/N에 해당한다. 여기서 $$ {\tau }_{\text{max}}=⌊∥{\mathit{r}}_1-{\mathit{r}}_2∥{\mathit{F}}_{\mathit{s}}/c⌋$$이고 c는 전달 속도이며, F_s는 샘플링 속도이다. 즉 DFT를 사용해서 시간 지연 추정할 때 모든 주파수가 필요한 것이 아니고, 주파수 2πτ_max/N까지만 필요하다는 뜻이 된다. 즉, 필요 주파수 폭이 있다는 의미가 된다. 따라서 푸리에 변환을 하기 전에 사용할 신호 데이터 X_W(f)에 미리 필요 주파수 이상을 차단하는 저역 통과 필터를 통과시켜서 잡음 성분을 미리 제거하면 시간 지연 추정 성능을 기대할 수 있다는 것을 의미한다. 더구나 두 수신기 간의 시간 지연 추정으로 방위를 추정하려고 할 때 두 센서를 잇는 선의 수직 방향을 0도로 하고 그 좌우로 일정 각도 범위만 관심을 두는 경우엔 저역 통과 필터의 차단 주파수를 이 유효 각도에 맞춰서 좀 더 좁게 조절해 쓸 수도 있음도 알 수 있다. 그림 2는 일반 GCC-PHAT에 저역 통과 필터를 적용하는 것을 보여주고 있다.

Fig. 2.

Diagram of GCC-PHAT using low-pass filter

Ⅲ. 모의실험을 통한 성능 비교

모의실험을 위해서 두 수신 채널을 위한 신호 열을 다음과 같이 발생시켰다.

비교실험을 위한 신호 발생은 식 (1)에서 원신호 s(n)의 경우 백색 가우시안 불규칙 신호로 발생시켰다. 이는 시스템 특성을 편향됨 없이 사용하기 위해서다. 이 원신호를 사용하여 두 번째 채널 신호가 첫 번째 채널 신호보다 10 샘플 뒤진 신호로 모델 하였다. 즉, x₂(n) = x₁(n−10) 이다. 이때 식 (1)과 같이 각 신호 x₁(n)과 x₂(n)에는 두 백색 가우시안 잡음, n₁(n)과 n₂(n)가 각각 부가되었다. 이들 부가 잡음 간에 서로 상관관계가 없도록 하였을 뿐만 아니라 원신호와도 상관관계가 없도록 하였다. 그리고 신호 대 잡음 비는 -10dB부터 10dB까지로 변화시켰다. 그리고 가상의 수신기 구성은 두 수신기간 거리는 10m로 설정하고 수신기는 수중에 설치한 것으로 가정하였다. 그리고 표본화 주파수는 8000 sample/sec로 가정하였다. 이 경우 수중 음파 전달 속도를 1500m/sec로 가정한다면, 최대 지연에 해당하는 시간 스텝은 53.3 스텝이다. 그리고 2장에서 서술한 것과 같이 역 푸리에 변환에 등가인 순방향 푸리에 변환으로 해석할 때 최대 지연 스텝 수에 대응하는 등가 주파수는 약 0.12π가 된다. 또 앞서 기술한 수신기 간 시간 지연을 10 샘플 스텝으로 할 때 이 시간 지연에 해당하는 등가 주파수는 약 0.03π가 된다. 이를 토대로 저역 통과 필터를 계산 시간에 부담을 주지 않는 간단한 구조의 2차 버터워스 필터로 만들고, 그 차단 주파수를 각각 0.2π, 0.12π 및 0.05π로 적용했을 때의 시간 지연 추정 성능을 저역 통과 필터를 사용하지 않는 일반 GCC-PHAT 방식 및 SSA를 추가로 사용하여 참고문헌[21]의 성능을 개선한 참고문헌[22] 방식으로 얻은 시간 지연 추정 성능과 비교해 보았다.

그림 3은 위와 같은 실험 환경설정 하에서 각 신호대 잡음 비에 대해서 100회씩 반복 시행하여 결과를 얻었다. 추정 성능 비교를 위해서 참 지연 값과 추정 지연 값 사이의 차이를 지연 시간 추정 오차라고 하고, 이 지연 시간 추정의 평균 자승 오차(Mean square error)를 각 신호 대 잡음 비에 대해서 그래프로 그렸다. 그림 3(a)는 모의 실험한 모든 신호 대 잡음 비에 대한 평균 자승 오차를 dB 값으로 나타낸 것이고, 그림 3(b)는 그림 3(a) 중 신호 대 잡음 비가 0dB에서 10dB 사이의 결과를 확대하여 그린 것이다.

Fig. 3.

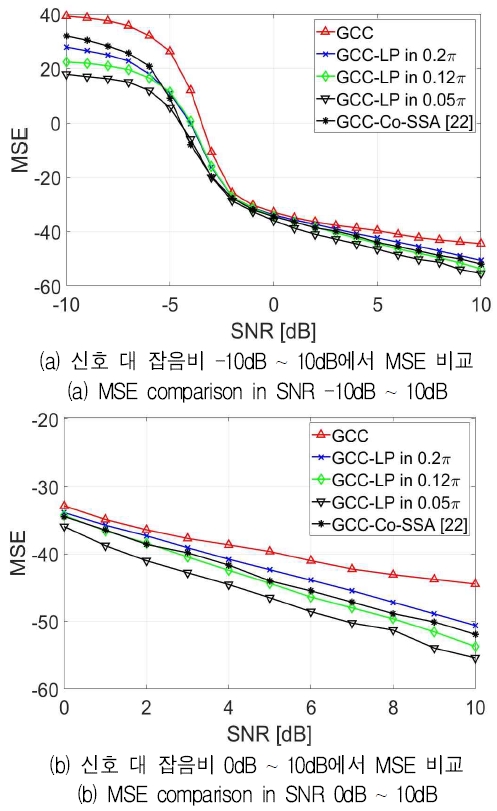
Performance comparison in case of white gaussian signal source.(GCC-LP: the proposed GCC using low pass filter)

그림 3(a)로 볼 때 GCC-PHAT의 추정 성능이 갑자기 나빠지는 문턱 현상의 향상 여부를 확인하기 위해서 -20dB를 지나는 신호 대 잡음 비를 비교하면, 참고문헌[22]의 방법과 차단 주파수가 0.05π인 저역 통과 필터를 사용하였을 때는 신호 대 잡음 비가 약 0.7dB 향상됨을 관찰할 수 있다. 차단 주파수가 0.12π나 0.2π인 경우는 신호 대 잡음 비 향상도가 0.2dB로 거의 비슷했다. 또 그림 3(b)에 보인 중저 수준 신호 대 잡음 비 구간인 신호 대 잡음 비가 0dB에서 10dB 구간에서의 추정 성능을 관찰하면, 추정 오차 향상 정도는 신호 대 잡음 비 0dB에서 GCC-PHAT 방법에 비해서 차단 주파수가 0.05π인 저역 통과 필터를 사용하였을 때 약 3dB 향상되었고, 차단 주파수가 0.12π인 저역 통과 필터를 사용하였을 때 약 1.3dB 향상되었고, 차단 주파수가 0.2π인 저역 통과 필터를 사용하였을 때 약 1dB 향상되었다. 신호 대 잡음 비 5dB에서는 GCC-PHAT 방법에 비해서 차단 주파수가 0.05π인 저역 통과 필터를 사용하였을 때 약 6.9dB 향상되었고, 차단 주파수가 0.12π인 저역 통과 필터를 사용하였을 때 약 4.7dB 향상되었고, 차단 주파수가 0.2π인 저역 통과 필터를 사용하였을 때 약 2.7dB 향상되었다. 신호 대 잡음 비 10dB에서는 GCC-PHAT 방법에 비해서 차단 주파수가 0.05π인 저역 통과 필터를 사용하였을 때 약 10.9dB 향상되었고, 차단 주파수가 0.12π인 저역 통과 필터를 사용하였을 때 약 9.2dB 향상되었고, 차단 주파수가 0.2π인 저역 통과 필터를 사용하였을 때 약 6.1dB 향상되었다. 결과 그림 전반적으로 보면 신호 대 잡음 비 0dBd에서 10dB 사이에는 차단 주파수가 0.05π인 저역 통과 필터를 사용한 경우가 제일 우수한 추정 결과가 나왔고, 그다음으로 차단 주파수가 0.12π인 저역 통과 필터를 사용한 경우이고 마지막이 차단 주파수가 0.2π인 저역 통과 필터를 사용한 경우라고 할 수 있다. 이에 비해서 참고문헌[22]의 방법은 차단 주파수가 0.12π인 저역 통과 필터를 사용하였을 때와 근접한 결과를 보였다. 즉 본 실험에서 두 수신기간 거리에 때문에 생기는 최대 지연 시간에 해당하는 주파수, 0.12π를 차단 주파수로 삼는 저역 통과 필터를 사용했을 때와 유사한 성능을 보였다.

실험 결과를 정리하면 2장에 기술한 내용을 바탕으로 그림 2에 도시한 것과 같이 GCC-PHAT 계산 과정 중에 저역 통과 필터를 추가로 사용하는 경우 불필요한 잡음 요소를 제거할 수 있어서 시간 지연 추정 성능이 향상됨을 확인할 수 있다.

Ⅳ. 결론 및 향후 과제

두 센서에 수신된 신호가 시간 지연을 추정하기 위한 GCC-PHAT 방법을 재해석해서 저역 통과 필터를 사용하면 신호의 잡음을 줄일 수 있음을 보였다. 그리고 모의실험을 통해서 다양한 차단 주파수의 저역 통과 필터를 사용하는 GCC-PHAT의 시간 지연 추정 성능을 다양한 신호 대 잡음 비에서 비교실험을 하였다. 그 결과 중저 수준 신호 대 잡음 비 구간에서 목표 시간 지연 값에 대응하는 주파수에 가까운 차단 주파수를 갖는 저역 통과 필터를 사용하는 GCC-PHAT의 추정 성능이 저역 통과 필터를 사용하지 않는 일반 GCC-PHAT에 비해서 더 향상되는 것을 확인하였다.

향후 본 연구는 실내 음향이나 수중 음향 분야에서 시간 지연 추정 성능 열화에 큰 영향을 미치는 잡음 환경인 임펄스성 잡음 환경에 적용하여 추정 성능 향상 가능성에 대해서 알아볼 예정이다.

Acknowledgments

본 논문은 2022년 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구임(No. KRIT-CT-22-023, 21-107-D00-012, 잠수함 표적식별 및 교전지원 지능화 기술)

References

• C. Knapp and G. Carter, "The generalized correlation method for estimation of time delay", IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 24, No. 4, pp. 320-327, Aug. 1976. [https://doi.org/10.1109/TASSP.1976.1162830]
• H. Xin, X. Bai, J. Zhao, and B. Li, "On TDE techniques for the radar signal", Journal of Engineering, Vol. 2019, No. 20, pp. 6554-6557, Oct. 2019. [https://doi.org/10.1049/joe.2019.0151]
• L. Qu, Q. Sun, T. Yang, L. Zhang, and Y. Sun, "Time-delay estimation for ground penetrating radar using ESPRIT with improved spatial smoothing technique", IEEE Geoscience and Remote Sensing Letters, Vol. 11, No. 8, pp. 1315-1319, Aug. 2014. [https://doi.org/10.1109/LGRS.2013.2292825]
• L. Nguyen, J. V. Miro, and X. Qiu, "Multilevel B-splines-based learning approach for sound source localization", IEEE Sensors Journal, Vol. 19, No. 10, pp. 3871–3881, May 2019. [https://doi.org/10.1109/JSEN.2019.2895854]
• B. Yegnanarayana, S. R. M. Prasanna, R. Duraiswami, and D. Zotkin, "Processing of reverberant speech for time-delay estimation", IEEE Transactions on Speech and Audio Processing, Vol. 13, No. 6, pp. 1110-1118, Nov. 2005. [https://doi.org/10.1109/TSA.2005.853005]
• J. Choi, J. Kim, and N. S. Kim, "Robust time-delay estimation for acoustic indoor localization in reverberant environments", IEEE Signal Processing Letters, Vol. 24, No. 2, pp. 226-230, Feb. 2017. [https://doi.org/10.1109/LSP.2016.2642178]
• R. A. Ershov, O. A. Morozov, and V. R. Fidelman, "A method for estimating the time delays during the signal propagation from the satellite communication systems with the code-division access", Radiophysics Quantum Electronics, Vol. 60, No. 7, pp. 561-570, Dec. 2017. [https://doi.org/10.1007/s11141-017-9827-6]
• J. Wang, J. Wang, X. Jia, W. Shan, and J. Guan, "Research on imaging methods of single-beam mechanical scanning sonar", 2020 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Macau, China, pp. 1-4, Aug. 2020. [https://doi.org/10.1109/ICSPCC50002.2020.9259472]
• V. Faerman, K. Voevodin, and V. Avramchuk, "Frequency-domain generalized phase transform method in pipeline leaks locating", High-Performance Computing Systems and Technologies in Scientific Research, Automation of Control and Production (HPCST 2022), pp. 22-38, Jan. 2023. [https://doi.org/10.1007/978-3-031-23744-7_3]
• C. Du, S. Yu, H. Yin, and Z. Sun, "Microseismic time delay estimation method based on continuous wavelet," Sensors, Vol. 22, No. 8, pp. 1-11, Apr. 2022. [https://doi.org/10.3390/s22082845]
• M. Azaria and D. Hertz, "Time delay estimation by generalized cross correlation methods", IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 32, No. 2, pp. 280-285, Apr. 1984. [https://doi.org/10.1109/TASSP.1984.1164314]
• D. Hertz, "Time delay estimation by combining efficient algorithms and generalized cross-correlation methods", IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 34, No. 1, pp. 1-7, Feb. 1986. [https://doi.org/10.1109/TASSP.1986.1164789]
• C. S. Tan, R. M. Mokhtar, and M. R. Arshad, "Improved generalized cross correlation phase transform algorithm for time difference of arrival estimation", Proc. of the 10th National Technical Seminar on Underwater System Technology 2018, Vol. 538, pp. 315-322, Feb. 2019. [https://doi.org/10.1007/978-981-13-3708-6_26]
• J. M. Lorenzo, R. V. Abad, P. R. Lopez, F. Rivas, and J. Escolano, "Evaluation of generalized cross-correlation methods for direction of arrival estimation using two microphones in real environments", Applied Acoustics, Vol. 73, No. 8, pp. 698-712, Aug. 2012. [https://doi.org/10.1016/j.apacoust.2012.02.002]
• T. Gustafsson, B. D. Rao, and M. Trivedi, "Source localization in reverberant environments: Modeling and statistical analysis", IEEE Transactions on Speech and Audio Processing, Vol. 11, No. 6, pp. 791-803, Nov. 2003. [https://doi.org/10.1109/TSA.2003.818027]
• X. Alameda-Pineda and R. Horaud, "Geometrically-constrained robust time delay estimation using non-coplanar microphone arrays", 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, pp. 1309-1313, Aug. 2012.
• J. S. Lim and K. Lee, "Time delay estimation algorithm using Elastic Net", The Journal of the Acoustical Society of Korea, Vol. 42, No. 4, pp. 364-369, Jul. 2023. [https://doi.org/10.7776/ASK.2023.42.4.364]
• J. Benesty, "Adaptive eigenvalue decomposition algorithm for passive acoustic source localization", J. Acoust. Soc. Amer., Vol. 107, No. 1, pp. 384-391, Jan. 2000. [https://doi.org/10.1121/1.428310]
• M. Moonen and D. Simon, "Robust adaptive time delay estimation for speaker localization in noisy and reverberant acoustic environments", EURASIP Journal on Advances in Signal Processing, Vol. 11, No. 10, pp. 1110-1124, Oct. 2003. [https://doi.org/10.1155/S111086570330602X]
• M. S. Brandstein, "A pitch-based approach to time-delay estimation of reverberant speech", Proc. of 1997 Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, pp. 1-4, Oct. 1997. [https://doi.org/10.1109/ASPAA.1997.625637]
• J. S. Lim, M. Cheong, and S. Kim, "Improved generalized cross correlation-phase transform based time delay estimation by frequency domain autocorrelation", The Journal of the Acoustical Society of Korea, Vol. 37, No. 5, pp. 271-275, Sep. 2018. [https://doi.org/10.7776/ASK.2018.37.5.271]
• J. Lim, "A Study on Improving Time Delay Estimation Performance of Generalized Cross Correlation-Phase Transform using Singular Spectrum Analysis", Journal of KIIT, Vol. 20, No. 8, pp. 99-106, Aug. 2022. [https://doi.org/10.14801/jkiit.2022.20.8.99]
• D. Salvati, C. Drioli, and G. L. Foresti, "Time Delay Estimation for Speaker Localization Using CNN-Based Parametrized GCC-PHAT Features", Proc. Interspeech 2021, pp. 1479-1483, Aug. 2021. [https://doi.org/10.21437/Interspeech.2021-988]
• A. Berg, M. O’Connor, K. Astrom, and M. Oskarsson, "Extending GCC-PHAT using Shift Equivariant Neural Networks", Proc. Interspeech 2022, pp. 1791-1795, Aug. 2022. [https://doi.org/10.21437/Interspeech.2022-524]