머신러닝을 이용한 인터리버 제원 블라인드 추정
초록
본 논문에서는 머신러닝을 이용하여 수신신호의 양이 제한적인 상황에서 인터리버 제원을 블라인드로 추정하는 기법을 제안한다. 비협력 상황에서 수신기는 송신기에서 사용한 통신제원을 알지 못하기 때문에 수신신호로부터 정보를 얻기 위해서 아무런 사전정보 없이 수신신호로부터 통신제원을 추정하여야 한다. 특히, 수신신호의 양이 제한적일 경우 블라인드 추정은 더욱 도전적인 과제이다. 최근 수신신호의 양이 제한적인 상황에서 인터리버 제원을 블라인드 추정하는 연구가 진행되었으나 추정 성능을 고도화하기 위하여 계산 복잡도가 증가하였다. 이를 해결하기 위하여 본 논문에서는 계산 복잡도가 감소된 머신러닝 기반의 블라인드 인터리버 제원 추정 알고리즘을 제안하며 컴퓨터 모의실험을 통해 본 논문에서 제안한 기법이 기존의 추정 기법보다 더 낮은 계산 복잡도에서도 동일한 성능으로 추정함을 보인다.
Abstract
In this paper, we propose a method for blind estimation of interleaver parameter using machine learning under the condition of scant received data. In non-cooperative contexts, since a receiver does not know communication parameters used by a transmitter, it has to estimate the communication parameters from a received data without any prior knowledge about the parameters to recover information from the received data. Specifically, it becomes more challenging under the condition of scant received data. Recently, estimation of interleaver parameter from scant received data has been researched. However, this method requires additional computational complexity in order to achieve an improved estimation performance. To deal with this problem, in this paper, we propose a blind interleaver parameter estimation method using machine learning with low computational complexity and, through computer simulations, we validate that the proposed method show the same estimation performance as in conventional methods with lower computational complexity.
Keywords:
blind detection, interleaver, machine learning, non-cooperative contextⅠ. 서 론
스펙트럼 감시, 무선 인지 라디오와 같은 비협력 상황에서 수신기는 송신기에서 신호를 생성하기 위해 사용한 통신제원을 알지 못한다. 이러한 상황에서 수신기는 수신신호로부터 정보를 얻기 위해 아무런 사전정보 없이 오직 수신신호에서 통신제원을 스스로 추정하여야 한다. 통신제원을 블라인드 추정하는 연구는 최근 많이 진행되어왔으며 여러 통신제원 가운데 본 논문에서는 인터리버 제원을 추정하는 기법을 제안한다.
인터리버와 채널부호는 여러 통신 채널에서 야기되는 다양한 손상들을 극복할 수 있게 해주기 때문에 안정적인 통신을 하기 위한 가장 중요한 통신 요소들 가운데 하나이다. 인터리버 제원 추정은 간단해 보이지만, 통신 제원 추정에서는 가장 어려운 부분 중 하나이다. 이에 따라, 인터리버 제원을 추정하기 위하여 많은 연구가 진행되어 왔다[1]-[16]. 참고문헌 [1]은 잡음이 없는 상황에서 수신신호로 구성된 행렬의 랭크를 이용하여 블록 인터리버 제원을 추정하는 기법을 제안하였다. 이를 발전시켜 [2]는 잡음이 존재하는 상황에서 인터리버 제원을 추정하는 기법을 제안하였다. 또한, 참고문헌 [3]-[9]은 행렬의 각 행과 열에 존재하는 비트 1 혹은 0의 개수를 이용하여 블록 인터리버, 길쌈 인터리버, helical 인터리버, helical scan 인터리버의 제원을 추정하는 기법들을 제안하였다. 인터리버 제원을 추정하기 위한 또 다른 기법은 랭크 분포를 이용하는 것이다[10]-[13]. 참고문헌 [10]은 수신신호를 이용하여 정방행렬을 구성하기 위해 오류가 적은 데이터를 선별하였고 [11]은 Kullback-Leibler Divergence (KLD)를 사용하여 제원을 추정하였다. 또한 참고문헌 [12]는 수신신호로 구성한 정방행렬들의 랭크 분포와 랜덤 비트로 구성된 정방행렬의 랭크 분포 간의 차이를 이용하였으며 [13]은 페이딩 채널과 같이 열악한 채널 상황에서도 동작하는 고도화된 인터리버 제원 파라미터 추정 기법을 제안하였다.
실제 신호를 수집하는 상황에서는 수신채널의 열화로 인한 수신신호의 품질 문제로 인터리버 제원을 추정하기 위해 사용될 수 있는 실질적인 수신신호의 양이 제한될 수 있다. 하지만 기존 인터리버 제원 추정 기법들은 충분히 많은 양의 수신신호가 확보되었음을 전제하였기 때문에 실제 확보할 수 있는 수신신호의 양이 제한적인 상황에서는 동작하지 않거나 추정 성능이 급격히 저하되는 문제점이 있었다. 이를 해결하기 위한 기법들이 최근에 연구가 진행되었다[14]-[16]. 확보할 수 있는 수신신호의 양이 부족한 경우, 이 문제를 해결하기 위하여 [14]는 수신신호를 결합하여 추가 데이터를 생성하였고 [15]는 부분행렬을 이용하는 기법을 제안하였다. 또한 참고문헌 [16]은 부분행렬의 곱을 이용하는 인터리버 제원 추정 기법을 제안하여 지금까지 수신신호의 양이 제한적인 상황에서 가장 좋은 성능을 가진다고 알려졌다. 그러나 [16]에서 제안하는 기법은 부분행렬의 곱을 사용하기 때문에 행렬 곱셈을 지속적으로 수행하여 계산 복잡도가 높고 인터리버 제원을 추정하는데 비교적 오랜 시간이 소요된다.
계산 복잡도 문제를 해결하기 위하여 본 논문에서는 머신러닝을 이용하여 수신신호의 양이 제한적인 상황에서 인터리버 제원을 블라인드로 추정하는 기법을 제안한다. 제안하는 기법은 수신신호를 이용하여 행렬을 구성한 뒤 임의의 열과 행을 삭제하여 다수의 부분행렬들을 구성한다. 이후 부분행렬들의 랭크 분포를 계산하여 이를 머신러닝에 입력하여 인터리버 제원을 추정한다. 머신러닝 모델 실제 구현을 고려하여 가장 간단한 support vector machine (SVM)을 적용한다. 컴퓨터 모의실험을 통해 본 논문에서 제안한 기법이 기존의 추정 기법보다 더 낮은 계산 복잡도에서도 동일한 성능으로 추정이 가능함을 보인다.
본 논문의 구성을 다음과 같다. 2장에서는 시스템 모델에 대하여 소개한다. 3장에서는 제안하는 머신러닝을 이용한 인터리버 제원 추정 기법을 설명한다. 4장에서는 컴퓨터 모의실험을 통해 본 논문에서 제안한 인터리버 제원 추정 기법의 성능을 분석하며, 5장에서 결론을 맺는다.
Ⅱ. 시스템 모델
송신기에서 부호어 길이가 nc이고 부호어 내의 메시지 비트의 길이가 kc인 (nc, kc) 선형 블록 부호와 인터리빙 주기가 L인 랜덤 인터리버를 사용한다고 가정하였다. 여기서 인터리빙 주기 L은 nc의 정수배이다.
비협력 통신 상황에서 수신기는 M 비트의 시퀀스 r을 길이의 n개의 행벡터들로 구분할 수 있다. 여기서 는 인터리빙 주기의 후보이며 n은 , ⌊ • ⌋는 내림함수이다. 수신신호 시퀀스 r과 i번째 행벡터 si는 각각 식 (1)과 (2)와 같이 나타낼 수 있다.
| (1) |
| (2) |
여기서 는 i번째 행벡터 si의 j번째 비트이고 , , 이다. 만약 n이 보다 크다면 n개의 행벡터들 가운데 개를 랜덤하게 선택하여 행으로 쌓아 크기의 정방행렬 R을 생성할 수 있다. 이 과정을 반복하면 총 개의 서로 다른 R을 생성할 수 있다, 여기서 xCy는 이항계수이다.
R의 랭크 부족은 와 L이 서로 같은 경우와 다른 경우인 두 가지 경우로 구분될 수 있다. 여기서 랭크 부족은 R의 랭크와 R의 행 혹은 열의 개수 간의 차이이다. 만약 와 L가 서로 다를 경우, R에서 부호어의 선형성이 사라진다. 이 경우 R의 랭크 부족 분포는 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 유사하다. 여기서 랜덤 비트로 이루어진 행렬의 랭크 부족 분포는 표 1과 같이 알려져 있다[17].
반대로 만약 와 L가 서로 같을 경우, R에는 부호어의 선형성이 유지되고 R의 랭크 부족 분포는 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 달라진다. 이러한 성질을 이용하여 [10]-[13]에서는 R의 랭크 부족 분포를 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 비교하여 인터리빙 주기를 추정하였다.
그러나 [10]-[13]에서 제시한 추정 기법은 다수의 R을 생성하여 랭크 부족 분포를 계산해야하기 때문에 단 하나의 R도 생성할 수 없을 정도로 수신신호의 양이 제한적인 상황에서는 [10]-[13]에서 제시한 기존 기법들이 동작하지 않는다. 이를 해결하기 위하여 [14]-[16]에서는 수신신호의 양을 매우 적게 필요로 하는 기법을 제안하였다. 참고문헌 [14]에서는 인터리빙 주기를 추정하기 위하여 si를 결합하여 새로운 벡터들을 생성하였고 [15]에서는 수신신호 전체를 사용하여 구성한 행렬로부터 부분행렬을 취하는 기법을 이용하였다. 그리고 [16]에서는 [15]에서 제안한 부분행렬을 곱하여 행렬을 추가로 생성하는 기법을 제안하여 추정 성능을 고도화하였다. 그러나 [16]에서 제안하는 기법은 부분행렬의 곱을 사용하기 때문에 행렬 곱셈을 지속적으로 수행하여 계산 복잡도가 높고 인터리버 제원을 추정하는데 비교적 오랜 시간이 소요된다.
계산 복잡도 문제를 해결하기 위하여 본 논문에서는 부분행렬의 곱을 사용하지 않고 기존의 기법과 동일한 추정 성능을 유지하는 머신러닝 기반 인터리빙 주기 추정 기법을 제안한다.
Ⅲ. 제안하는 인터리빙 주기 추정 기법
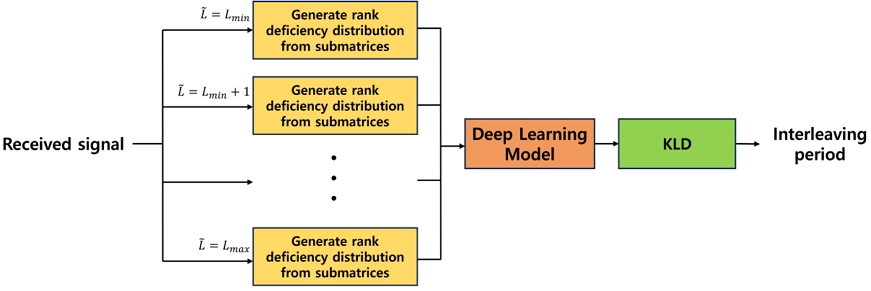
본 장에서는 머신러닝을 이용한 인터리빙 주기 추정 기법을 제안한다. 그림 1은 본 논문에서 제안하는 인터리빙 주기 추정 기법의 흐름도이다. 먼저 를 Lmin부터 Lmax까지 변화해가며 수신신호로부터 행렬을 구성한 뒤 부분행렬을 다수 생성하여 랭크 부족 분포를 계산한다. 이후 랭크 부족 분포를 머신러닝의 입력으로 이용하여 인터리빙 주기를 추정한다. 여기서 Lmin과 Lmax는 각각 중 가장 작은 값과 가장 큰 값이다.
우선 참고문헌 [16]에서 제안한 기법과 같이 수신신호 시퀀스 r로부터 n개의 행벡터 si를 생성한 뒤, si를 행으로 쌓아 크기의 행렬 Rd를 식 (3)과 같이 구성한다.
| (3) |
행렬 Rd로부터 임의로 행과 열을 삭제하여 l×l크기의 부분행렬 Rs를 생성할 수 있다. 여기서 l은 부분행렬의 행의 개수이며 보다 작은 양의 정수이다. 이때 총 개의 서로 다른 Rs를 생성할 수 있다. 이때 Rs의 랭크 부족 분포는 2장에서 설명한 R의 랭크 부족 분포와 같은 성질을 보인다[15]. 만약 와 L가 서로 다를 경우, Rs에서 부호어의 선형성이 사라지기 때문에 Rs의 랭크 부족 분포는 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 유사하다. 반대로 만약 와 L가 서로 같을 경우, Rs에는 부호어의 선형성이 유지된다. 이 경우 Rs의 랭크 부족 분포는 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 달라진다.
를 변화시켜 가며 얻은 Rs의 랭크 부족 분포는 인터리빙 주기를 추정하기 위한 머신러닝 모델에 입력된다. 본 논문에서는 실제 적용을 고려하여 머신러닝 모델로 SVM을 사용한다. SVM은 입력 데이터를 경계로 분리시키는 머신러닝 모델의 일종이다. 이때 SVM은 단지 두 종류의 입력 데이터를 분리하는 것뿐만 아니라, 한 종류의 입력 데이터를 학습하여 입력 데이터와 서로 다른 성질을 지니는 이상 데이터를 구분할 수 있다[18]. 따라서 본 논문에서는 를 Lmin부터 Lmax까지 변화해 가며 구성한 Rs의 랭크 부족 분포 데이터를 4차원 벡터로 구성하여 훈련 데이터로서 SVM 모델을 훈련시켰다. 이때 만약 테스트 데이터로 와 L가 서로 다를 경우에서 Rs의 랭크 부족 분포가 입력되면, 이는 훈련 데이터와 유사하기 때문에 높은 SVM 점수가 출력될 것이다. 반대로 만약 테스트 데이터가 와 L가 같을 경우의 Rs의 랭크 부족 분포라면, 이는 훈련 데이터와 다르기 때문에 낮은 SVM 점수가 출력될 것이다. 따라서 본 논문에서는 인터리빙 주기를 추정하기 위해 SVM 출력 점수가 가장 낮을 때의 를 실제 인러티빙 주기로 추정하였다.
하지만, 잡음이 많은 통신 상황에서는 와 L이 같은 경우에도 오류가 발생한 비트로 인하여 Rs의 랭크 부족 분포가 랜덤 비트로 이루어진 행렬의 랭크 부족 분포와 유사해질 수 있으며, 이에 따라 SVM 출력 점수가 가장 낮을 때의 가 실제 인터리빙 주기가 아닐 가능성이 존재한다. 이와 같은 오경보를 방지하기 위하여 본 논문에서는 두 가지 분포의 유사도를 측정하기 위해 일반적으로 이용되는 KLD를 사용한다[11]. KLD는 두 분포 간의 상대 엔트로피를 계산하기 때문에 두 분포가 비슷한 경우 0에 가까운 값을 가지고 두 분포가 서로 다른 경우 상대적으로 큰 값을 가지게 된다. 따라서 본 논문에서는 오경보를 제어하기 위하여 SVM을 통해 검출된 일 때의 랭크 부족 분포와 랜덤 비트로 이루어진 행렬의 랭크 부족 분포 간의 KLD 값이 임계값 γ보다 큰 경우에만 실제 인터리빙 주기가 추정되었다고 선언한다. 여기서 γ는 오경보를 제어하기 위한 설계 파라미터이며 γ가 클수록 오경보가 적게 발생한다. 머신러닝을 이용한 인터리버 주기 추정 기법을 알고리즘으로 요약하여 나타내면 표 2와 같다.
Ⅳ. 모의실험 및 성능 분석
본 장에서는 모델 학습 및 테스트를 위한 데이터셋에 대하여 설명하고, 컴퓨터 모의실험을 통하여 수신 데이터의 양이 제한적인 경우 머신러닝 기반의 인터리버 제원 추정 기법의 성능을 추정 정확도, 오경보 발생 횟수, 계산 복잡도 측면에서 분석한다. 또한 기존의 인터리버 제원 추정 기법 [16]의 성능을 추가하여 제안하는 머신러닝 기반 인터리버 제원 추정 기법의 성능과 비교한다. 모의실험을 위한 조건은 표 3과 같다.
본 논문의 모델 학습 및 테스트 데이터셋 구성 방식은 다음과 같다. 먼저 제안하는 모델의 학습을 위해 수신 데이터의 수량 별로 100,000개의 랭크 부족 분포로 구성된 데이터셋을 생성하였다. 이때 데이터셋의 랭크 부족 분포는 오류가 발생하지 않은 신호를 통해 구성되었으며 데이터셋은 9:1의 비율로 각각 와 L이 서로 다를 때와 와 L가 같을 때의 랭크 부족 분포로 구성되었다. 여기서 랭크 부족 분포는 1,000개의 서로 다른 Rs를 구성하여 계산되었다.
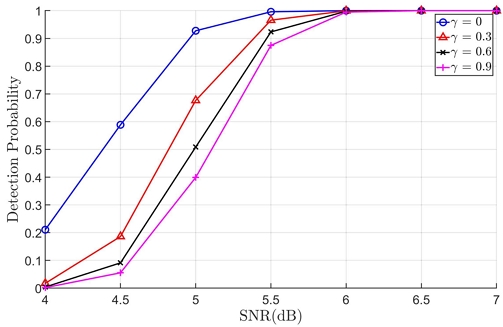
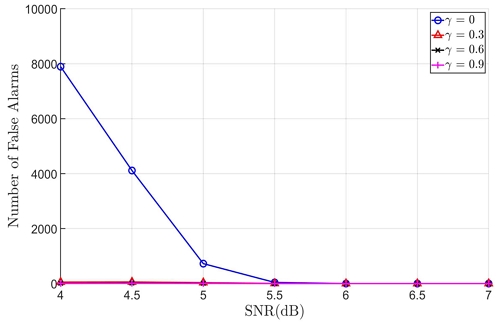
그림 2와 3에는 M이 3240(60×60×0.9) 비트, (15, 11) BCH 코드, 인터리빙 주기 60이 사용되었을 때 오경보를 제어하기 위한 파라미터인 γ에 따른 추정 정확도와 오경보 발생 횟수를 각각 나타내었다. 그림 2와 3을 통해 γ가 작아짐에 따라 추정 정확도가 증가하지만 오경보 발생 횟수도 동시에 증가하고 있는 것을 확인할 수 있다. 따라서 γ에 따른 추정 정확도와 오경보 발생 횟수 사이에는 트레이드 오프 관계가 있으며 본 논문에서는 γ를 설계 파라미터로 설정한다.
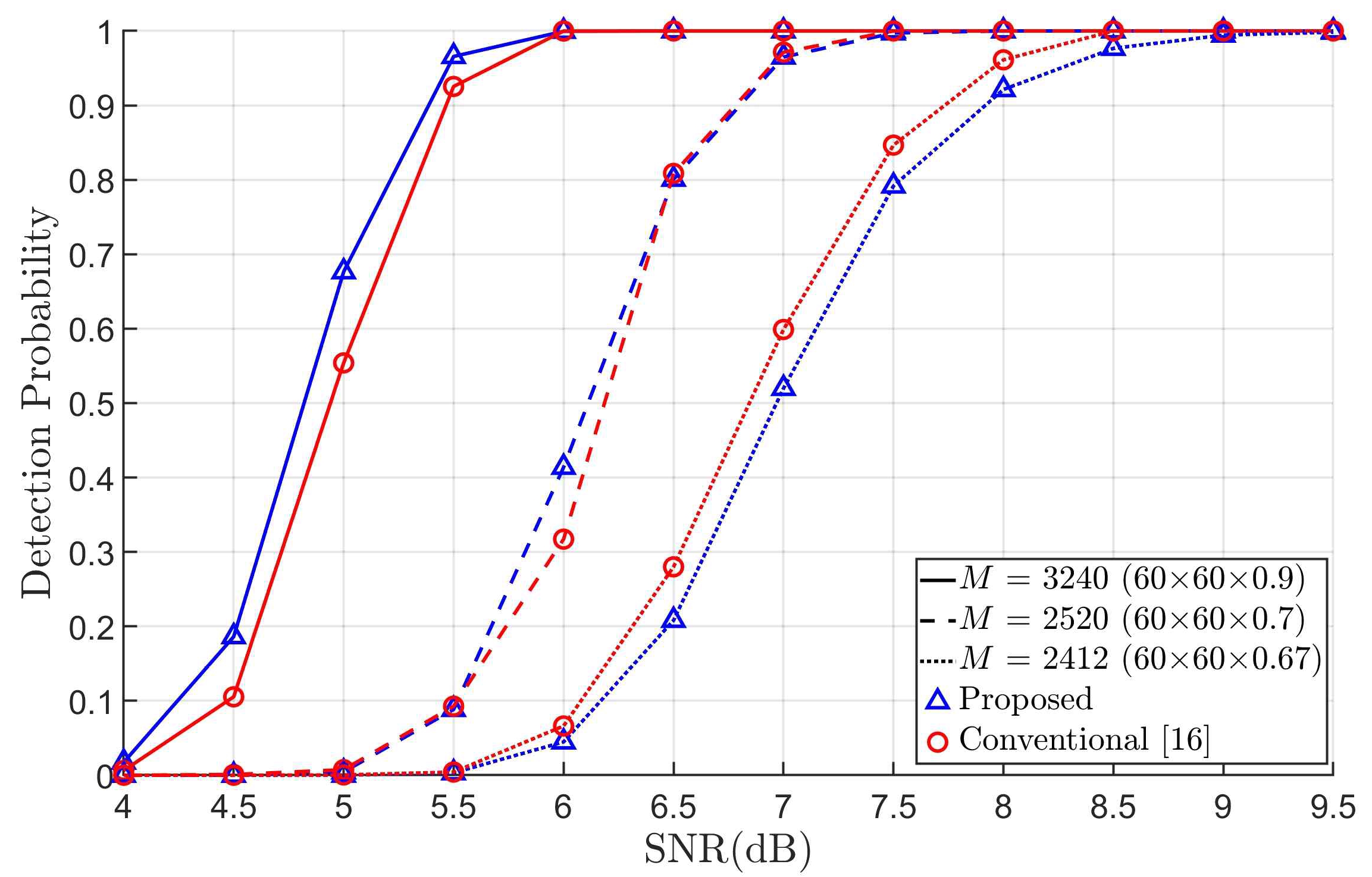
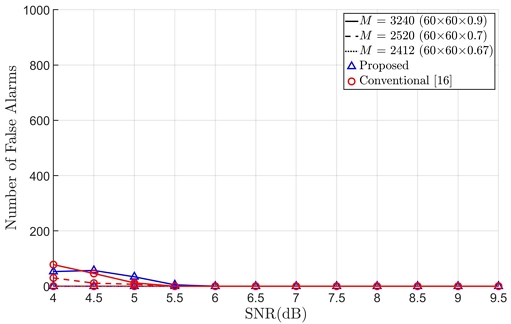
수신신호의 양에 따른 제안하는 기법의 성능을 분석하기 위하여 그림 4와 5에는 γ가 0.3이고 (15, 11) BCH 코드, 인터리빙 주기 60이 사용되었을 때 M에 따른 추정 정확도와 오경보 발생 횟수를 각각 나타내었다. 성능 비교를 위하여 [16]에서 제안한 기법의 성능을 그림 4와 5에 추가하였다.
그림 4와 5로부터 제안한 기법과 기존 기법의 추정 성능이 유사한 것을 확인할 수 있다. 특히, M이 3412(60×60×0.67) 비트일 때는 기존 기법이 추정 정확도 90% 기준 약 0.18 dB의 신호 대 잡음비(signal-to-noise ratio, SNR) 이득을 가지고 M이 3240(60×60×0.9) 비트일 때는 제안하는 기법이 추정 정확도 90% 기준 약 0.26 dB의 SNR이득을 가지는 것을 확인할 수 있다.
계산 복잡도 측면에서 기존 기법은 수신신호가 한정적인 상황에서 인터리빙 주기를 추정하기 위해 행렬 곱셈을 매번 수행하기 때문에 행렬 곱셈을 수행하지 않는 머신러닝 기반 인터리빙 주기 추정 기법보다 계산 복잡도가 높을 것으로 생각할 수 있다. 표 4에는 M이 3240(60×60×0.9) 비트일 때 제안하는 기법과 기존 추정 기법의 평균 수행 시간을 나타내었다. 이때 수행 시간은 각 기법을 100번 수행한 평균으로 구하였다. 표 4를 통해 제안하는 기법이 기존 추정 기법에 비하여 계산 복잡도 측면에서 우수성을 보이는 것을 확인할 수 있다. 모의실험 결과를 통해 제안하는 기법의 수행 시간이 기존 추정 기법의 수행시간의 약 12% 수준으로 감소하여 제안하는 기법이 기존 기법과 유사한 인터리빙 주기 추정 성능을 유지하면서 빠른 추정이 가능함을 알 수 있다.
Ⅴ. 결론 및 향후 과제
비협력 상황에서 수신기는 송신기에서 사용한 통신 제원을 추정하여야 한다. 본 논문에서는 머신러닝을 이용하여 수신신호의 양이 제한적인 상황에서 인터리버 제원을 블라인드로 추정하는 기법을 제안하였다. 제안하는 기법은 우선 수신신호를 이용하여 행렬을 구성한 뒤 임의의 열과 행을 삭제하여 다수의 부분행렬들을 구성하였다.
이후 부분행렬들의 랭크 분포를 계산하고 이를 머신러닝에 입력하여 인터리버 제원을 추정하였다. 머신러닝 모델로는 구현 복잡도를 고려한 실제 적용을 위하여 SVM을 채택하였다. 컴퓨터 모의 실험을 통해 제안한 기법이 기존 기법과 유사한 추정 정확도와 오경보 발생 횟수를 가지며 제안한 기법은 수행 시간 기준 기존 기법의 수행 시간의 약 12% 수준으로 감소된 계산 복잡도를 가짐을 보였다. 향후에는 유사한 계산 복잡도를 가지면서 추정 정확도가 보다 향상된 인터리버 제원 추정 기법 개발이 수행되어야 할 것으로 사료된다.
Acknowledgments
본 연구는 ㈜LIG넥스원 비협력 통신 신호 분석 기반 기술 연구 과제의 지원을 받아 수행되었음
References
- G. Burel and R. Gautier, "Blind estimation of encoder and interleaver characteristics in a non-cooperative context", in Proc. IASTED, Scottsdale, AZ, USA, pp. 275-280, Nov. 2003.
-
G. Sicot, S. Houcke, and J. Barbier, "Blind detection of interleaver parameters", Signal Process., Vol. 89, No. 4, pp. 450-462, Apr. 2009.
[https://doi.org/10.1016/j.sigpro.2008.09.012]

-
J. Jeong, D. Yoon, J. Lee, and S. Choi, "Blind reconstruction of a helical scan interleaver", in Proc. IEEE ICICS, Singapore, pp. 1-4, Dec. 2011.
[https://doi.org/10.1109/ICICS.2011.6174276]

-
J. Jeong, J. Oh, H. Lim, and D. Yoon, "Estimation of interleaver parameters for punctured channel coded signals in noisy channels", Journal of KIIT, Vol. 14, No. 11, pp. 49-57, Nov. 2016.
[https://doi.org/10.14801/jkiit.2016.14.11.49]

-
R. Swaminathan, A. S. Madhukumar, W. T. Ng, and C. M. S. See, "Parameter estimation of block and helical scan interleavers in the presence of bit errors", Digit. Signal Process., Vol. 60, pp. 20-32, Jan. 2017.
[https://doi.org/10.1016/j.dsp.2016.08.006]

-
S. Ramabadran, A. S. Madhukumar, N. W. Teck, and C. M. S. See, "Parameter estimation of convolutional and helical interleavers in a noisy environment", IEEE Access, Vol. 5, pp. 6151-6167, Mar. 2017.
[https://doi.org/10.1109/ACCESS.2017.2684189]

-
R. Swaminathan and A. S. Madhukumar, "Classification of error correcting codes and estimation of interleaver parameters in a noisy transmission environment", IEEE Trans. Broadcast., Vol. 63, No. 3, pp. 463-478, Sep. 2017.
[https://doi.org/10.1109/TBC.2017.2704436]

-
R. Swaminathan, A. S. Madhukumar, G. Wang, and T. S. Kee, "Blind reconstruction of Reed-Solomon encoder and interleavers over noisy environment", IEEE Trans. Broadcast., Vol. 64, No. 4, pp. 830-845, Dec. 2018.
[https://doi.org/10.1109/TBC.2018.2795461]

-
Y. Xu, Y. Zhong, and Z. Huang, "An improved blind recognition method of the convolutional interleaver parameters in a noisy channel", IEEE Access, Vol. 7, pp. 101775-101784, Jul. 2019.
[https://doi.org/10.1109/ACCESS.2019.2930663]

-
C. Choi and D. Yoon, "Enhanced blind interleaver parameters estimation algorithm for noisy environment", IEEE Access, Vol. 6, pp. 5910-5915, Sep. 2017.
[https://doi.org/10.1109/ACCESS.2017.2754638]

-
C. Choi and D. Yoon, "Blind interleaver parameter estimation using Kullback-Leibler divergence", Journal of KIIT, Vol. 15, No. 12, pp. 109-115, Dec. 2017.
[https://doi.org/10.14801/jkiit.2017.15.12.109]

-
C. Choi and D. Yoon, "Novel blind interleaver parameter estimation in a noncooperative context", IEEE Trans. Aerosp. Electron. Syst., Vol. 55, No. 4, pp. 2079-2085, Aug. 2019.
[https://doi.org/10.1109/TAES.2018.2875570]

-
G. Kim, M. Jang, and D. Yoon, "Improved method for interleaving parameter estimation in a non-cooperative context", IEEE Access, Vol. 7, pp. 92171-92175, Jul. 2019.
[https://doi.org/10.1109/ACCESS.2019.2927078]

-
M. Jang, G. Kim, Y. Kim, and D. Yoon, "Blind estimation of interleaver parameter with a limited number of data", IEEE Access, Vol. 8, pp. 69160-69166, Apr. 2020.
[https://doi.org/10.1109/ACCESS.2020.2986273]

-
M. Jang, G. Kim, D. Kim, and D. Yoon, "Blind interleaver parameter estimation from scant data", IEEE Access, Vol. 8, pp. 217282-217289, Dec. 2020.
[https://doi.org/10.1109/ACCESS.2020.3041795]

-
Y. Jung, M. Jang, and D. Yoon, "Improved method for blind interleaver parameter estimation using matrix multiplication from scant data", IEEE Access, Vol. 9, pp. 138209-138214, Oct. 2021.
[https://doi.org/10.1109/ACCESS.2021.3117869]

-
V. G. Kolchin, Random Graphs, NewYork, USA: CUP, 1998.
[https://doi.org/10.1017/cbo9780511721342]

-
Y. Jang, T. Lee, and D. Yoon, "New decision for QAM based on SVM for complex impairments", IEEE Trans. Veh. Technol., Vol. 72, No. 4, pp. 4815-4828, Apr. 2023.
[https://doi.org/10.1109/TVT.2022.3226576]


2019년 2월 : 한양대학교 융합전자공학부(공학사)
2019년 3월 ~ 현재 : 한양대학교 융합전자공학과 석박사통합과정
관심분야 : 무선 및 이동 통신 시스템, 통신이론

2009년 2월 : 한양대학교 전자통신컴퓨터공학부(공학사)
2015년 2월 : 한양대학교 전자컴퓨터통신공학과(공학박사)
2015년 3월 ~ 2023년 2월 : 국방과학연구소 선임연구원
2023년 3월 ~ 현재 : 제주대학교 통신공학과 조교수
관심분야 : 통신이론, 전자기스펙트럼전, 기계학습 기반 통신 시스템, 광대역 신호처리

2013년 2월 : 세종대학교 정보통신공학과(공학사)
2012년 2월 ~ 현재 : LIG넥스원 선임연구원
관심분야 : 디지털 통신 시스템, 통신신호처리 알고리즘

1989년 2월 : 한양대학교 전자통신공학과(공학사)
1992년 2월 : 한양대학교 전자통신공학과(공학석사)
1995년 8월 : 한양대학교 전자통신전파공학과(공학박사)
2004년 3월 ~ 현재 : 한양대학교 융합전자공학부 교수
관심분야 : 통신이론, 위성 및 우주통신, 추정 및 검출