개선된 손실 함수를 이용한 딥러닝 기반 자동 변조 분류
초록
자동 변조 분류(AMC, Automatic Modulation Classification)는 현대 무선 통신의 주요 기술 중 하나로 다양한 협력 및 비협력 통신에서 중요한 역할을 한다. 최근 다양한 딥러닝(DL, Deep Learning) 기반의 AMC에 대한 연구가 보고되고 있다. 본 논문에서는 AMC를 위한 DL 모델의 손실 함수를 개선하여 분류 성능을 향상시키는 방법을 제안하고 분류 성능을 분석한다. 제안하는 방법은 기존의 소프트맥스 손실 함수를 각 변조 방식에 대한 확률분포가 목표 확률분포에 더 가깝게 조절될 수 있도록 개선한다. 컴퓨터 모의실험을 통해 다양한 DL 모델에 대해 제안한 방법으로 개선한 손실 함수를 적용하여 기존보다 분류 정확도 측면에서 성능을 향상시킬 수 있음을 확인한다.
Abstract
Automatic Modulation Classification(AMC) is one of the key technologies of modern wireless communication which plays an important role in various cooperative and non-cooperative contexts. Recently, many studies on Deep Learning(DL)-based AMC have been reported. This paper proposes a method for improving classification performance by modifying the loss function of the DL model for AMC and analyzes its classification performance. The proposed method improves the conventional softmax loss function to adjust the probability distribution over the modulation schemes closer to the desired probability distribution. Through computer simulations, we verify that by applying the loss function revised with the proposed method, it is possible to improve performance in terms of classification accuracy for various DL models than conventional ones.
Keywords:
automatic modulation classification, non-cooperative context, cognitive radio, spectrum surveillance, deep learningⅠ. 서 론
현대 무선 통신의 주요 기술 중 하나로 송신 신호에 사용된 변조 방식을 수신기에서 사전 정보 없이 식별하는 자동 변조 분류(AMC, Automatic Modulation Classification)가 있다. AMC는 인지 무선(Cognitive radio) 및 스펙트럼 감시(Spectrum surveillance)와 같은 다양한 협력 및 비협력 통신에서 중요한 역할을 한다. 고전적인 AMC 기법은 주로 수신 신호로부터 계산한 각 변조 방식 별 우도(Likelihood) 또는 특징(Feature) 값을 기반으로 송신 신호에 사용된 변조 방식을 예측한다. 우도 기반 AMC는 수신 신호로부터 계산한 우도 비를 사전에 정의한 문턱 값과 비교하여 변조 분류를 수행하는 방법으로[1]-[5], 최적의 분류 성능을 제공하지만 정확한 우도 비 계산을 위해 채널의 정보를 모두 알고 있어야 하고 계산 복잡도가 높아 실제 상황에서는 사용하기 어렵다. 특징 값 기반 AMC는 수신 신호로부터 적절한 특징 값을 계산한 뒤 그를 이용하여 변조 방식을 예측하는 방법으로[6]-[13], 우도 기반의 AMC 기법에 비해 분류 성능은 낮지만 채널의 정보를 요구하지 않고 계산 복잡도의 이점이 있다.
고전적인 특징 값 기반 AMC에서는 각 변조 방식별로 뚜렷이 구분되는, 신호의 특성에 대한 전문적인 연구를 통해 엄선된 수치들을 특징 값으로 이용한다. 최근에는 이러한 특징 값을 딥러닝(DL, Deep Learning) 모델을 이용해 자동으로 추출하여 변조 방식을 분류하는 연구가 활발히 이뤄지고 있다[14]-[19]. 다양한 단일 및 다중 반송파 신호를 분류 대상으로 한 연구가 이뤄졌으며, 단일 반송파 신호의 경우 참고문헌 [14]는 수신 신호의 동위상 및 직교 위상(I/Q. In-phase and Quadrature) 성분으로 구성된 데이터를 합성곱 신경망(CNN, Convolutional Neural Network)에 입력하여 11종류의 변조 방식을 분류하였고, 참고문헌 [15]는 수신 신호로부터 성상도(Constellation) 이미지를 생성한 뒤 AlexNet, GoogLeNet과 같은 다양한 이미지 분류 모델에 입력하여 8가지 변조 방식을 분류하였다. 또한 참고문헌 [16]은 8종류의 변조 방식을 수신 신호의 I/Q 성분으로 구성된 데이터와 성상도 이미지의 2종류의 데이터로 각각 훈련시킨 2개의 CNN을 통해 계층적으로 분류하였다. 이러한 CNN을 이용한 연구 외에도, 참고문헌 [17]에서는 신호의 I/Q 성분으로 구성된 데이터를 장단기 기억(LSTM, Long Short-term Memory) 모델에 입력하여 4가지 변조 방식을 분류하였다. 다중 반송파 신호의 경우 참고문헌 [18]과 [19]에서 OFDM(Orthogonal Frequency Division Multiplexing) 신호의 각각 4가지, 5가지의 부반송파 변조 방식을 수신 신호의 I/Q 성분으로 구성된 데이터와 CNN을 이용하여 분류하는 연구가 수행되었다.
일반적으로 AMC를 위한 DL 모델의 훈련은 충분한 양의 데이터를 통해 모델의 예측 오류를 정량화한 손실 함수를 최적화함으로써 이루어진다. 가장 널리 사용되는 손실 함수는 소프트맥스(Softmax) 손실 함수로, 목표 확률분포와 모델의 출력으로부터 얻은 소프트맥스 확률분포 사이의 평균 교차 엔트로피(Cross entropy)로 정의된다. 본 논문에서는 모델의 분류 성능 향상을 위해 모델의 손실 함수를 개선하는 방법을 제안한다. 제안하는 방법은 모델의 출력 대신 그것을 특정한 사상(Mapping)을 통해 변환한 것을 이용하여 평균 교차 엔트로피를 계산한다. 제안한 방법으로 개선된 손실 함수를 통해 각 변조 방식에 대한 확률분포를 목표 확률분포에 기존보다 더 가깝게 조절하여 모델의 분류 성능을 향상시킬 수 있다. 다양한 DL 모델에 대한 컴퓨터 모의실험을 통해 제안한 방법으로 개선한 손실 함수를 적용하여 기존보다 분류 정확도 측면에서 성능을 향상시킬 수 있음을 확인한다.
본 논문의 구성은 다음과 같다. 2장에서는 본 논문에서 가정하는 시스템 모델에 대해 설명한다. 3장에서는 제안하는 손실 함수 개선 방법을 설명한다. 4장에서는 컴퓨터 모의실험을 통해 제안하는 방법을 적용한 다양한 DL 모델의 분류 성능을 분석하며, 5장에서 결론을 제시한다.
Ⅱ. 시스템 모델
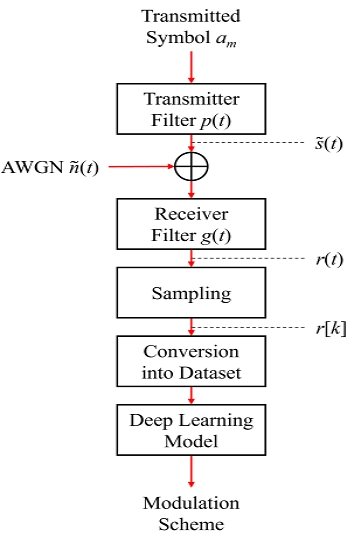
이 장에서는 본 논문에서 가정하는 시스템 모델을 설명한다. 그림 1은 DL 기반 AMC에 대한 시스템 모델을 나타낸 것이다.
본 논문에서는 심볼 시간(Symbol duration)이 Tsym인 송신 심볼 am이 가산 백색 가우스 잡음(AWGN, Additive White Gaussian Noise) 채널을 거쳐 수신되는 상황을 가정한다. 송신 필터를 고려한 송신 신호 ★는 식 (1)과 같이 나타낼 수 있다.
| (1) |
여기서 p(t)는 송신기 필터를 나타낸다. 송신된 신호 ★는 AWGN ★가 더해져서 수신기에 도달한 후 수신기 필터를 통과하여 식 (2)와 같이 최종적으로 수신된다.
| (2) |
여기서 r(t)는 수신 신호를, g(t)는 수신기 필터를 나타낸다. 이후 수신기에서는 r(t)를 일정한 주기 Ts마다 샘플링되어 이산시간 신호 r[k]=r(kTs)를 얻고 이를 이용하여 송신 신호에 사용된 변조 분류를 수행한다. r[k]를 DL 모델에 적합한 형태의 데이터로 변환한 뒤, 모델에 그 데이터를 입력하여 송신 신호에 사용된 변조 방식을 예측한다.
그림 1에서 AMC를 위해 사용되는 DL 모델은 일반적으로 충분한 양의 데이터를 통해 모델의 예측 오류를 정량화한 손실 함수를 최적화하여 사전에 훈련된다. 본 논문에서는 모델의 분류 성능 향상을 위해 이러한 손실 함수를 개선하는 방법을 제안하며, 이어지는 장에서 이에 대해 자세히 설명한다.
Ⅲ. 제안하는 손실 함수 개선 방법
이 장에서는 소프트맥스 손실 함수에 대해 간략하게 설명한 뒤 이를 개선할 수 있는 방법을 설명한다.
서로 다른 K개의 클래스(Class)를 분류하는 DL 모델을 N개의 Example로 구성된 데이터셋 X를 이용하여 훈련시키는 상황을 고려하고, X의 i번째 Example을 Xi, 그것의 라벨(Label)을 y(i)라 하자. Xi에 대한 모델의 출력 f(i)는 식 (3)과 같은 K차원 벡터이다.
| (3) |
여기서 T는 전치(Transpose) 연산을 나타낸다. 소프트맥스 손실 함수는 다음과 같이 f(i)로부터 K개의 클래스에 대한 확률분포를 얻은 뒤 이를 이용하여 데이터셋 X에 대한 모델의 예측 오류를 정량화한다. 먼저 식 (4)와 같이 f(i)를 변환하여 각 클래스에 대한 확률분포를 얻는다.
| (4) |
여기서 ★는 f(i)를 변환하여 얻은 확률분포로 소프트맥스 확률분포라 하며 식 (4)의 변환 softmax( • )을 소프트맥스 함수라 부른다. 다음으로 식 (5)와 같이 목표 확률분포 ★와 ★ 사이의 교차 엔트로피를 구하여 Example Xi에 대한 모델의 예측 오류를 정량화한다.
| (5) |
여기서 L(i)는 Xi에 대한 모델의 예측 오류를, ★는 y(i)번째 성분이 1이고 나머지 원소가 모두 0인 원-핫 벡터(One-hot Vector)를 나타낸다. 마지막으로 식 (5)의 L(i)의 모든 Example에 대한 평균을 구하여 식 (6)과 같이 데이터셋 X에 대한 모델의 예측 오류를 정량화한 소프트맥스 손실 함수를 계산한다.
| (6) |
여기서 Lsoftmax는 소프트맥스 손실 함수를 나타낸다.
식 (6)의 Lsoftmax를 최적화함에 따라 소프트맥스 확률분포 ★는 목표 확률분포 ★에 가까워지며, 이는 ★의 y(i)번째 성분 ★가 증가함을 의미한다. 따라서 결과적으로 모델은 출력 f(i)가 다음 조건을 만족하도록 훈련된다.
| (7) |
본 논문에서는 Xi에 대한 K개 클래스의 소프트맥스 확률분포가 ★에 기존보다 가까워질 수 있도록 손실 함수를 개선한다. 이를 위해, 다음과 같은 과정을 통해 소프트맥스 손실 함수 Lsoftmax를 f(i)가 식 (7)보다 더 엄격한 조건을 만족하도록 모델이 훈련될 수 있게 수정한다. 먼저 식 (6)의 손실 함수를 식 (8)과 같이 다시 쓴다.
| (8) |
식 (8)의 ★를 식 (9)와 같은 구간별로 정의된 선형 함수 ψ를 통해 변형하여 식 (8)의 소프트맥스 손실 함수 Lsoftmax를 식 (10)과 같은 새로운 손실 함수 Lmodified로 변형한다.
| (9) |
| (10) |
여기서 β는 0 이상 1 이하의 실수이다. 식 (10)과 같이 소프트맥스 손실 함수를 매개변수 β를 도입하여 수정함으로써 모델의 분류 성능을 향상시킬 수 있으며, 그 이유는 다음과 같다. 식 (10)은 ★와 식 (11)과 같은 확률분포 ★ 사이의 평균 교차 엔트로피와 같다.
| (11) |
또, 식 (11)의 ★은 식 (12)의 벡터 ★를 소프트맥스 함수를 통해 변환한 것과 같다.
| (12) |
즉, 새로운 손실 함수 Lmodified는 모델의 출력 f(i) 대신 그것을 사상 ψ를 통해 변환한 ★를 통해 K개의 클래스에 대한 새로운 확률분포 ★를 얻고 이를 이용하여 목표 확률분포 ★와의 평균 교차 엔트로피를 계산한 것이다. 여기서 ★는 모델의 훈련 과정에서만 고려하는 확률분포이며 모델을 테스트할 땐 여전히 소프트맥스 확률분포 ★를 이용함을 유의하라. Lmodified를 최적화함에 따라 ★가 ★에 가까워지며, 결과적으로 모델은 출력 f(i)가 다음 조건을 만족하도록 훈련된다.
| (13) |
0 ≤ β ≤1이므로 식 (13)에서 ★이고, 따라서 식 (13)을 만족하는 ★는 식 (7)을 만족하는 ★보다 커질 수 있다. 이를 통해 각 클래스에 대한 소프트맥스 확률분포를 ★에 기존보다 더 가깝게 조절할 수 있으며, 이를 통해 모델의 분류 정확도를 향상시킬 수 있다.
본 논문에서는 새로운 손실 함수 Lmodified의 매개변수 β를 하이퍼파라미터(Hyperparameter)로 두고 모델 및 데이터셋에 따라 β의 적절한 값을 실험적으로 찾아 사용한다.
Ⅳ. 모의실험 및 성능 분석
이 장에서는 컴퓨터 모의실험을 통해 본 논문에서 제안한 손실 함수 개선 방법을 실험적으로 검증한다. 검증을 위해 다양한 DL 모델에 제안하는 방법을 통해 개선된 새로운 손실 함수와 기존의 소프트맥스 손실 함수를 적용하고 각각의 성능을 분류 정확도 관점에서 비교한다.
먼저 모의실험을 위한 DL 모델 및 데이터셋에 대해 설명한 뒤, DL 모델별 변조 분류 성능을 비교한다. 본 논문에서는 참고문헌 [14]과 [17]에서 제시된, AMC를 위한 2가지 DL 모델을 이용하여 실험을 진행하였다. 참고문헌 [14]의 모델은 2개의 합성곱층(Convolutional Layer)과 2개의 완전연결층으로 이뤄진 CNN으로, 표 1에 그 구조를 나타내었다. 표 1에서 conv(H×W, C)는 H×W 커널(Kernel)을 사용하고 출력 채널(Channel)이 C개인 합성곱층을, linear(U)는 출력 유닛(Unit)이 U개인 완전연결층을, Nmod는 분류 대상 변조 방식의 수를 의미한다. 참고문헌 [17]의 모델은 3개의 LSTM층과 4개의 완전연결층으로 이뤄진, 표 2에 나타낸 것과 같은 구조의 모델이다. 표 2에서 LSTM(h)는 은닉 상태(Hidden State)의 차원이 h인 LSTM층을 나타내며 나머지 표기는 표 1과 동일하다.
본 논문에서 고려한 2가지 DL 모델을 위한 데이터셋에 대해 설명하면 다음과 같다. 본 논문에서는 모든 실험에 대해 BPSK(Binary Phase Shift-keying), QPSK(Quadrature Phase Shift-keying), 8PSK(8-ary Phase Shift-keying), 16QAM(16-ary Quadrature Amplitude Modulation), 64QAM(64-ary Quadrature Amplitude Modulation)의 5가지 변조 방식을 고려하고 수신 신호로 송·수신기 필터로 롤 오프율(Roll-off Rate)이 0.22인 제곱근 올림 코사인 필터(Root Raised Cosine Filter)를 사용하고 Ts = Tsym/4인, 4배 오버샘플링(Oversampling)된 신호를 가정하였다. 이산시간 신호 r[k]를 각 모델에 적합한 형태의 데이터로 변환하는 과정은 다음과 같다. 두 모델은 모두 r[k]의 I/Q 성분으로 구성된 배열을 입력으로 받는다. 먼저 r[k]의 실수부와 허수부를 분리하여 식 (14)와 같은 벡터 r[k]를 구성한다.
| (14) |
여기서 Re{ • }와 Im{ • }은 각각 복소수의 실수부와 허수부를 나타낸다. 다음으로, L개의 r[k]를 연접하여 2×L 배열을 구성하고 이를 모델을 위한 데이터셋의 각 Example로 사용한다. 참고문헌 [14]의 모델에는 첫 번째 Layer인 conv1에 맞게 2×L 배열 전체를 한 번에 입력하고, 참고문헌 [17]의 모델에는 첫 번째 Layer인 LSTM1에 맞게 배열의 각 2차원 열벡터를 하나의 타임스텝(Timestep)으로 하여 L개의 열을 순서대로 입력한다. 본 논문에서는 L=800으로 설정하여 실험을 진행한다. 모델의 훈련, 검증, 테스트를 위한 데이터셋의 세부 수치는 다음과 같다. 모델 훈련 및 검증을 위해서는 각 Example의 Es/N0가 구간 [6, 20] 사이의 균일 분포 U(6, 20) dB를 따르는 데이터셋을 사용하였으며 이때 각각 변조 방식 당 40,000개, 10,000개의 Example로 훈련 및 검증 셋을 구성하였다. 모델 테스트를 위해서는 Es/N0 및 변조 방식 당 10,000개의 Example로 이뤄진 테스트 셋을 구성하였으며 Es/N0=[6, 8, ... , 20] dB에 대해 각각 테스트 셋을 생성하였다.
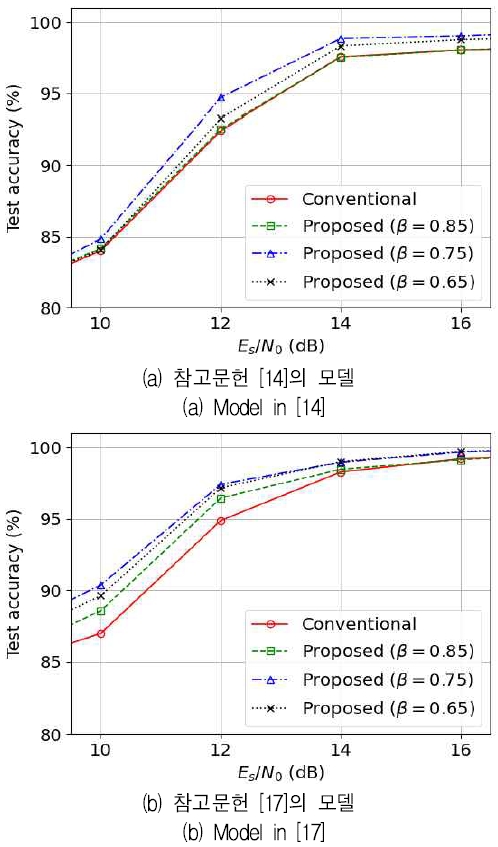
편의를 위해 본 논문에서 제안한 방법을 통해 개선한 손실 함수를 제안하는 손실 함수라 부르자. 먼저 β=0.85, 0.75, 0.65인 제안하는 손실 함수를 적용한 모델의 성능을 기존의 손실 함수를 적용한 모델의 성능과 비교하였다. 그림 2는 각 모델의 Es/N0에 따른 분류 정확도를 모델 구조별로 나타낸 것이다. 그림 2(a)에서 참고문헌 [14]의 모델은 β=0.85인 제안한 손실 함수를 적용하는 경우 기존의 손실 함수를 적용할 때와 분류 성능의 차이가 거의 없으며, β=0.75, 0.65로 더 작은 제안한 손실 함수를 적용하는 경우 기존의 손실 함수를 적용할 때보다 각각 약 0.86 dB, 0.32 dB 낮은 Es/N0에서 모델이 분류 정확도 95%를 달성하여 성능이 향상되는 것을 볼 수 있다. 또, 그림 2(b)에서 참고문헌 [17]의 모델은 β=0.85, 0.75, 0.65인 제안한 손실 함수를 적용하는 경우 모두 기존의 손실 함수를 적용할 때보다 분류 정확도 95% 기준 각각 약 0.43 dB, 0.75 dB, 0.64 dB의 Es/N0 이득을 얻는 것을 확인할 수 있다.
이러한 그림 2의 결과로부터 제안한 손실 함수를 이용하여 기존보다 분류 정확도를 향상시킬 수 있으며 β의 값에 따른 분류 정확도의 경향은 모델마다 다른 것을 확인할 수 있다.
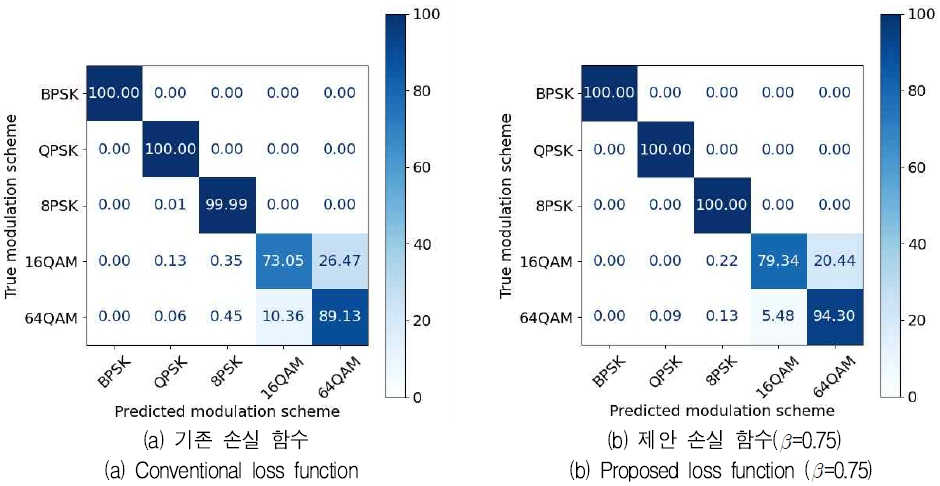
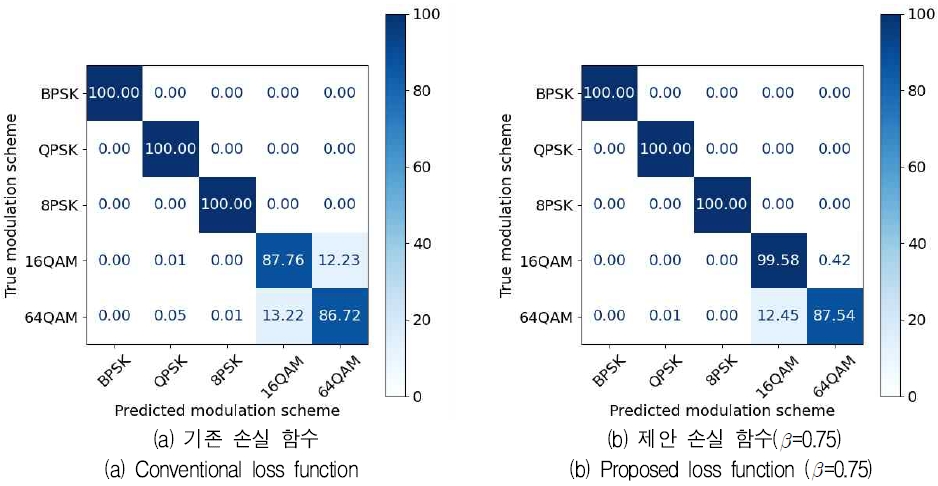
앞서 설명한 DL 모델들의 손실 함수에 따른 변조 분류 성능 변화를 보다 자세히 분석하기 위해, 그림 3과 4에 각각 참고문헌 [14]의 모델과 참고문헌 [17]의 모델에 기존 및 제안한 손실 함수를 적용하는 경우에 대한 혼동 행렬을 나타내었으며, 이때 제안한 손실 함수의 β의 값은 앞선 실험의 결과를 바탕으로 0.75를 선택하였다. 그림 3과 4에서 두 모델 모두 제안한 새로운 손실 함수를 적용하는 경우 기존의 손실 함수를 적용할 때보다 16QAM과 64QAM의 분류 정확도가 향상되고 두 변조 방식 사이의 혼동이 감소하는 것을 관찰할 수 있다.
이러한 결과를 통해 제안한 손실 함수를 적용함으로써 분류 성능에 주된 영향을 미치는, 상대적으로 높은 차수의 변조 방식의 분류 성능을 개선할 수 있음을 확인할 수 있다.
Ⅴ. 결 론
본 논문에서는 DL을 이용한 AMC에서 모델의 손실 함수를 개선하여 분류 성능을 향상시키는 방법을 제안하였다. 제안하는 방법은 기존의 소프트맥스 손실 함수를 각 변조 방식에 대한 확률분포가 목표 확률분포에 더 가깝게 조절될 수 있도록 변형하였다. 컴퓨터 모의실험을 통해 다양한 DL 모델에 제안한 방법으로 개선한 손실 함수를 적용하여 기존보다 분류 정확도 95% 기준 최대 약 0.86 dB의 Es/N0 이득을 얻을 수 있음을 확인하였다. 향후에는 보다 많은 변조 방식을 고려하고 분류 성능을 더욱 향상시킬 수 있는 손실 함수에 대한 추가적인 연구가 계속되어야 할 것으로 사료된다.
Acknowledgments
본 연구는 ㈜LIG넥스원 비협력 통신 신호 분석 기반 기술 연구 과제의 지원을 받아 수행되었음
References
-
O. A. Dobre, A. Abdi, Y. Bar-Ness, and W. Su, "Survey of automatic modulation classification techniques: Classical approaches and new trends", IET Communications, Vol. 1, No. 2, pp. 137-156, Apr. 2007.
[https://doi.org/10.1049/iet-com:20050176]

-
F. Hameed, O. A. Dobre, and D. C. Popescu, "On the likelihood-based approach to modulation classification", IEEE Transactions on Wireless Communications, Vol. 8, No. 12, pp. 5884-5892, Dec. 2009.
[https://doi.org/10.1109/TWC.2009.12.080883]

-
W. Wei and J. M. Mendel, "Maximum likelihood classification for digital amplitude-phase modulations", IEEE Transactions on Communications, Vol. 48, No. 2, pp. 189-193, Feb. 2000.
[https://doi.org/10.1109/26.823550]

-
C.-Y. Huang and A. Polydoros, "Likelihood methods for MPSK modulation classification", IEEE Transactions on Communications, Vol. 43, No. 2, pp. 1493-1504, Feb. 1995.
[https://doi.org/10.1109/26.380199]

-
V. G. Chavali and C. R. C. M. da Silva, "Maximum-likelihood classification of digital amplitude-phase modulated signals in flat fading non-Gaussian channels", IEEE Transactions on Communications, Vol. 59, No. 8, pp. 2051-2056, Aug. 2011.
[https://doi.org/10.1109/TCOMM.2011.051711.100184]

-
S. S. Soliman and S.-Z. Hsue, "Signal classification using statistical moments", IEEE Transactions on Communications, Vol. 40, No. 5, pp. 908-916, May 1992.
[https://doi.org/10.1109/26.141456]

-
Y. Yang and S. S. Soliman, "A suboptimal algorithm for modulation classification", IEEE Transactions on Aerospace and Electronic Systems, Vol. 33, No. 1, pp. 38-45, Jan. 1997.
[https://doi.org/10.1109/7.570706]

-
E. E. Azzouz and A. K. Nandi, "Automatic identification of digital modulation types", Signal Processing, Vol. 47, No. 1, pp. 55-59, Nov. 1995.
[https://doi.org/10.1016/0165-1684(95)00099-2]

-
A. Swami and B. M. Sadler, "Hierarchical digital modulation classification using cumulants", IEEE Transactions on Communications, Vol. 48, No. 3, pp. 416-429, Mar. 2000.
[https://doi.org/10.1109/26.837045]

-
H. Wu, M. Saquib, and Z. Yun, "Novel automatic modulation classification using cumulant features for communications via multipath channels", IEEE Transactions on Wireless Communications, Vol. 7, No. 8, pp. 3098-3105, Aug. 2008.
[https://doi.org/10.1109/TWC.2008.070015]

-
J. Lee, S. Ahn, J. Choi, and D. Yoon, "Phase mapping recognition and modulation classification algorithm using new higher-order cumulants", Journal of KIIT, Vol. 15, No. 2, pp. 153-160, Feb. 2017.
[https://doi.org/10.14801/jkiit.2017.15.2.153]

-
S. Ahn, D. Yoon, S. Yun, and J. Kwon, "Enhanced modulation classification algorithm robust to phase and frequency offsets", Journal of KIIT, Vol. 16, No. 5, pp. 47-52, May 2018.
[https://doi.org/10.14801/jkiit.2018.16.5.47]

-
J. Lee, J. Kim, B. Kim, D. Yoon, and J. Choi, "Robust automatic modulation classification technique for fading channels via deep neural network", Entropy, Vol. 19, No. 9, pp. 1-11, Aug. 2017.
[https://doi.org/10.3390/e19090454]

- T. O’Shea and N. West, "Radio machine learning dataset generation with GNU radio", in Proc. GNU Radio Conference, Boulder, CO, USA, Vol. 1, No. 1, pp. 1-6, Sep. 2016.
-
S. Peng, H. Jiang, H. Wang, H. Alwageed, Y. Zhou, M. M. Sebdani, and Y.-D. Yao, "Modulation classification based on signal constellation diagrams and deep learning", IEEE Transactions on Neural Networks and Learning Systems, Vol. 30, No. 3, pp. 718-727, Mar. 2019.
[https://doi.org/10.1109/TNNLS.2018.2850703]

-
Y. Wang, J. Yang, and G. Gui, "Data-driven deep learning for automatic modulation recognition in cognitive radios", IEEE Transactions on Vehicular Technology, Vol. 68, No. 4, pp. 4074-4077, Apr. 2019.
[https://doi.org/10.1109/TVT.2019.2900460]

-
S. Hu, Y. Pei, and Y.-C. Liang, "Deep neural network for robust modulation classification under uncertain noise conditions", IEEE Transactions on Vehicular Technology, Vol. 69, No. 1, pp. 564-577, Jan. 2020.
[https://doi.org/10.1109/TVT.2019.2951594]

-
G. Song, M. Jang, and D. Yoon, "CNN-based automatic modulation classification in OFDM systems", 2022 International Conference on Computer, Information and Telecommunication Systems (CITS), Piraeus, Greece, pp. 1-4, Jul. 2022.
[https://doi.org/10.1109/CITS55221.2022.9832989]

-
G. Song, M. Jang, and D. Yoon, "Deep learning-based modulation identification for OFDM systems", 2023 30th International Conference on Systems, Signals and Image Processing (IWSSIP), Ohrid, North Macedonia, pp. 1-4, Jun. 2023.
[https://doi.org/10.1109/IWSSIP58668.2023.10180258]


2021년 2월 : 한양대학교 융합전자공학부(공학사)
2021년 3월 ~ 현재 : 한양대학교 융합전자공학과 석박사통합과정
관심분야 : 무선 및 이동 통신 시스템, 머신러닝, 신호정보

2009년 2월 : 인천대학교 정보통신공학과(공학사)
2011년 2월 : 한양대학교 전자컴퓨터통신공학과(공학석사)
2011년 1월 ~ 2011년 12월 : 한국항공우주산업 연구원
2012년 1월 ~ 현재 : LIG넥스원 수석연구원
관심분야 : 전자전 안테나, 통신 전자전 시스템

2015년 2월 : 세종대학교 정보통신공학과(공학사)
2017년 2월 : 세종대학교 정보통신공학과(공학석사)
2021년 2월 : 세종대학교 정보통신공학과(공학박사)
2021년 4월 ~ 2021년 11월 : 세종대학교 정보통신공학과 박사후연구원
2022년 5월 ~ 현재 : LIG넥스원 선임연구원
관심분야 : 디지털 통신 시스템, 통신신호처리 알고리즘

1989년 2월 : 한양대학교 전자통신공학과(공학사)
1992년 2월 : 한양대학교 전자통신공학과(공학석사)
1995년 8월 : 한양대학교 전자통신전파공학과(공학박사)
2004년 3월 ~ 현재 : 한양대학교 융합전자공학부 교수
관심분야 : 통신이론, 위성 및 우주통신, 추정 및 검출