물리정보 신경망을 활용한 미국형 옵션 가격 결정
초록
본 논문은 미국형 풋 옵션 평가에 물리정보 신경망(PINN)을 적용하는 방법을 탐구한다. 유한 차분법 및 이항 트리와 같은 전통적인 방법은 일반적으로 사용되지만, 계산 효율성 관련된 문제에 직면한다. PINN은 블랙-숄즈 편미분방정식 및 경계 조건을 신경망 훈련 과정에 직접 통합함으로써 유망한 대안을 제공한다. 우리 PINN 모델은 미분 가능성과 목표 데이터 샘플링을 위해 Softplus 함수를 포함한 기술을 사용하여 성능을 향상시킨다. 우리는 모델을 유한 차분법 및 이항 방법과 비교하여 동등한 정확성을 입증했다. 또한, 제거 연구는 손실함수의 미분 가능성과 충격 영역 근처의 목표 데이터의 중요성을 강조한다. 이러한 결과는 복잡한 금융 모델링 작업에 대해 전통적인 수치 방법과 현대적인 기계 학습 접근 방식의 잠재력을 보여준다.
Abstract
This paper explores the application of Physics-Informed Neural Networks(PINNs) to the valuation of American put options. Traditional methods such as the finite difference method and binomial trees are commonly used but face challenges related to computational efficiency. PINNs offer a promising alternative by incorporating the Black-Scholes partial differential equation(PDE) and its boundary conditions directly into the neural network training process. Our PINN model uses advanced techniques, including the Softplus function for smoothing and targeted data sampling, to enhance performance. We benchmarked our model against finite difference methods and binomial methods, demonstrating comparable accuracy. Additionally, an ablation study highlights the importance of smoothness of loss functions and targeted data near shock regions. The results underscore the potential of combining traditional numerical methods with modern machine learning approaches for complex financial modeling tasks.
Keywords:
american options, PINN, option pricing, black-scholes equation, financial modelingⅠ. 서 론
미국 옵션, 특히 미국형 풋 옵션의 평가 문제는 양적 금융에서 매우 중요하다. 유럽형 옵션과 달리 미국 옵션은 만기 전에 언제든지 행사할 수 있어 가격 결정에 추가적인 복잡성이 더해진다. 전통적인 수치 방법인 유한 차분법(Finite difference method) 및 이항 트리는 이 문제를 해결하는 데 널리 사용되어 왔다. 그러나 이러한 방법은 복잡한 경계 조건 및 고차원 문제를 처리할 때 계산 효율성과 정확성에 관련된 문제에 직면하는 경우가 많다.
최근 몇 년간, 기계 학습 기술, 특히 딥러닝이 복잡한 금융 모델링 작업을 해결하는 데 큰 가능성을 보여주었다. 예를들어, H. S. Lee and S. H. Oh[1]는 시계열 자료를 활용해 기업의 신용도를 평가하기 위한 방법으로 LSTM(Long Short Term Memory)를 제시한 바 있다. 특히 M. Raissi et al.[2]의 고안한 물리정보 신경망(PINN)은 딥러닝의 강력함을 전통적인 수치 방법의 견고성과 통합한 강력한 도구로 떠오르고 있다. PINN은 문제를 지배하는 기본 물리 법칙을 편미분방정식으로 입력하여 편미분방정식의 해를 직접 학습한다. 이러한 접근 방식은 학습된 솔루션이 물리적 원칙을 준수하도록 하여 보다 정확하고 신뢰할 수 있는 모델을 제공한다.
본 논문은 미국형 풋 옵션의 가격 결정에 PINN을 적용하는 방법을 탐구한다. 우리는 블랙-숄즈 PDE 및 관련 경계 조건과 종결 조건을 신경망 학습 과정에 직접 통합하는 데 중점을 둔다. 우리 모델은 불연속점을 처리하고 손실함수를 미분 가능하게 하도록 Softplus 함수를 사용하고, 도메인 전체에서 정확한 학습을 보장하기 위해 포괄적인 데이터 샘플링 전략을 활용한다.
또한, BTCS 유한 차분법 및 이항 방법과 같은 전통적인 방법과 우리의 PINN 모델을 비교하여 정확성과 계산 효율성 측면에서 그 효능을 입증한다. 우리는 또한 모델 성능에 대한 종결 조건의 미분 가능성과 및 충격 근처 데이터 샘플링의 영향을 조사하기 위해 제거 연구를 수행한다.
방법론적 기여 외에도 우리의 PINN 모델의 유연성과 확장 가능성을 강조한다. 전통적인 방법과 달리, 우리 모델은 변동성 σ, 행사가 K, 이자율 r 등의 추가 입력을 쉽게 수용할 수 있다. 더욱이, PINN의 구조는 다중 자산 미국형 옵션 가격 결정과 같은 다차원 문제로 쉽게 확장될 수 있어 다양한 금융 응용 프로그램에 적합한 도구가 된다.
이 논문의 나머지 부분은 다음과 같이 구성된다. 2장에서는 옵션 가격 결정 및 PINN에 관한 관련 문헌을 검토한다. 3장에서는 미국형 옵션과 PINN에 대한 이론적 배경을 소개한다. 4장에서는 데이터 생성 및 손실함수 설계를 포함한 방법론 등 모델 구현 세부 사항을 제시한다. 5장에서는 옵션 가격 결과, 제거 연구 및 계산 시간 분석을 포함한 결과를 논의한다. 마지막으로, 6장에서는 연구 결과 요약 및 향후 연구 방향을 제시한다.
Ⅱ. 관련 연구
2.1 미국형 옵션
권리 행사가 만기 시점에만 가능한 유럽형 옵션과는 달리 미국형 옵션은 만기 이전 시점에서도 권리를 행사할 수 있다. 이는 옵션의 보유자가 옵션을 행사할 시기를 결정해야 한다는 문제, 즉 최적 멈춤 문제(Optimal stop problem)를 제기한다. 옵션의 가격을 기초자산의 가격과 시간에 대한 함수로 정의할 때, 기초자산의 가격이 내가격(In-The-Money)일 경우 옵션을 즉시 행사하게 되고 외가격(Out-of-The-Money)일 경우 상황이 유리해질 때까지 옵션을 보유하게 되는데 이에 따라 최적의 옵션 행사 가격에 대한 자유 경계(Free boundary)가 발생하게 된다. 미국형 콜 옵션은 유럽형 콜 옵션과 동일한 가치를 갖는다는 것이 수학적으로 증명된 바 있지만 풋 옵션은 해석적인 해를 구하는 것이 불가능하다. 이에 미국형 풋 옵션의 가격과 경계에 대한 함수를 구하기 위해 다양한 수치해석적 방법들이 제시된 바 있다.
먼저 M. J. Brennan and E. S. Schwartz[3]는 유한차분법을 활용해 블랙-숄즈 방정식을 BTCS 알고리즘으로 변형시킨 후 경계조건을 설정함으로써 미국형 풋 옵션의 가격을 구한 바 있다.
B. F. Nielsen et al.[4]는 Front-fixing method와 Penalty method를 제시했는데 Frong-fixing method는 블랙-숄즈 방정식의 기초자산 가격과 옵션 가격 변수를 경계 함수를 이용해 변형시킴으로써 경계를 제거한 후 유한차분법을 통해 가격을 구하였다. Penalty Method에서는 블랙-숄즈 방정식에 penalty term을 추가한 후 유한차분법으로 가격을 계산하였다. K. Muthuraman[5]은 경계에 대한 초기의 추측을 바탕으로 가격 함수를 구한 후 이를 통해 수렴에 이르기까지 경계와 가격 함수를 반복적으로 구하는 Moving Boundary Approach를 제시했고 이후 A. Chockalingam and K. Muthuraman[6]과 함께 이를 개량한 Approximate Moving Boundary를 보였다.
한편, 이러한 수치해석적 방법들 외의 다른 방법들도 제시되었는데 S. P. Zhu[7]는 Homotopy analysis를 이용해 무한급수 형태의 닫힌 해를 제시했다. 동일한 만기와 행사가격을 가진 유럽형 옵션의 가격을 초기 추측값으로 활용하면 30개 항의 합으로 수렴하는 결과를 얻을 수 있음을 밝혔다.
최근에는 기계 학습을 이용하여 미국형 풋 옵션의 가격과 행사 경계를 구하려는 움직임이 대두되고 있다. F. Gatta et al.[8]은 PINN을 이용한 미국형 풋 옵션의 가격과 행사 경계에 대한 연구를 발표했다. 기존의 수치해석적 방법들과는 다르게 이산화(Discretization)가 필요하지 않고 기초자산이 여러 개인 자산에 대한 연구도 진행할 수 있다는 장점이 있다. Gatta는 이 연구에서 변수의 개수에 따라 parametric, non-parametric, semi-parametric 세 가지 모형을 제시했다. 또한, Gatta의 연구에서는 블랙-숄즈 모형의 학습을 위한 모델과 자유 경계 함수를 결정하기 위한 모델, 두 가지 모델을 제안하였다.
본 논문 또한 PINN을 활용하여 미국형 풋옵션을 계산하는 것이지만 방법론에서 Gatta의 연구와 큰 차이가 있다. Gatta의 연구의 경우에는 미국형 옵션의 행사 여부를 결정하는 자유 경계에 초점이 맞춰져 있다. Gatta의 연구에서는 자유 경계를 결정하기 위한 모델과 블랙-숄즈 방정식을 풀기 위한 모델 두 가지 모델을 활용하였다. 이러한 두 가지 모델의 활용은 자유 경계를 정확하게 결정할 수 있지만, 학습 과정이 복잡해지며 고차원으로 확장이 힘들어진다. 우리 논문에서는 Gatta의 연구와 달리 자유 경계를 고려하지 않는다. 대신, 하나의 방정식을 사용하여 미국 옵션의 행사 여부를 처리한다. 이 접근 방식을 통해 미국 옵션의 가격을 정확하게 산정할 수 있다.
2.2 데이터 샘플링 연구
주어진 데이터가 비교적 적은 금융 분야에서는 데이터 샘플링 및 전처리가 중요하다. M. Kim et al.[9]은 개인 신용 평가 모델을 위해서 데이터 증강 기법을 적용하여 모델의 성능을 향상시켰다. 마찬가지로 PINN을 훈련하려면 데이터의 전처리 및 샘플링이 필요하다. Z. Mao and X. Meng[10]은 잔차와 기울기를 기반으로 하는 ASM(Adaptive Sampling Method)을 제시했다. Mao와 Meng은 Burgers equation과 Euler equation에 이 방식을 적용하였고 잔차와 기울기까지 고려한 ASM이 잔차만을 고려한 ASM보다 성능이 우수하다는 것을 보였다.
Z. Gao et al.[11]은 신경망의 실패 가능성까지 고려한 FI-PINN(Failure-Informed PINN)을 제시했다. 실패 확률을 추정하기 위한 샘플링 방법으로 몬테카를로 방법과 중요도 샘플링 방법이 제시되었으나 이 방법들은 비효율적이거나 계산에 필요한 분포함수를 알 수 없다는 단점이 있다. Gao는 이를 보완하기 위한 SAIS(Self-Adaptive Importance Sampling)를 제시했다. Gao는 특이해를 갖는 편미분방정식과 시간에 의존하는 편미분방정식에서 SAIS가 다른 샘플링 방법들보다 더 정확히 예측했음을 보였다.
2.3 PINN 옵션 가격 결정
Y. Bai et al.[12]은 유럽형 옵션 가격 산출을 위한 블랙-숄즈 방정식을 풀기 위해 기존의 PINN을 개량한 Improved PINN(IPINN)을 고안했다. IPINN에는 각 층의 출력값이 다음 층의 입력값이 된다는 구조는 유지하되 국소 적응형 활성화 함수가 도입하였다. Bai는 PINN과 비교했을 때 IPINN이 더 빠른 수렴 속도와 향상된 성능을 보였음을 밝혔다.
X. Wang et al.[13]은 기초자산이 2개인 바이너리 옵션과 녹아웃 옵션의 가격을 산출하기 위해 PINN을 사용했다. R. U. Seydel[14]이 몬테카를로 방법을 이용해 구한 바이너리 옵션과 유한요소법으로 구한 녹아웃 옵션의 가격과 비교했을 때 거의 차이가 없었다.
A. Dhiman and Y. Hu[15]는 PINN을 과거의 시장 데이터로 훈련시켜 비교하는 데 그치지 않고 실시간 시장 데이터와 비교했고 기존의 해석적 방법이나 수치적 방법보다 PINN이 더 시장 데이터와 근접했음을 보였다.
Ⅲ. 이론적 배경
3.1 미국형 풋 옵션
본 연구에서 다룰 대상은 기초자산이 하나인 미국형 풋 옵션이다. 미국형 풋 옵션은 주어진 만기 시점인 T 이전에 언제든지 기초자산을 정해진 행사 가격인 K에 팔 수 있는 권리를 갖는 계약이다. 즉 권리를 행사 했을떄 다음과 같이 정의된 금액만큼 이익을 취할 수 있다.
| (1) |
식 (1)를 바탕으로 옵션의 가격 P는 기초자산의 가격인 S와 시간을 나타내는 t를 변수로 갖는 함수인 P(S,t)로 표현할 수 있다. 기초자산 가격의 범위는 0에서부터 상한선 Smax까지인 [0,Smax]이고 시간의 범위는 [0, T]이다. 따라서 P(S,t)의 정의역은 다음과 같다.
| (2) |
이론상으로는 기초자산의 가격에는 상한선이 없지만, 구간이 무한대일 경우 계산에 어려움이 따르므로 식 (2)와 같이 가격의 상한선인 Smax를 정할 필요가 있다.
미국형 옵션은 권리 행사 여부에 따라서 함수의 정의역 Ω을 두 영역으로 나눌 수 있다. 이때 두 영역을 구분하는 자유 경계를 B(t)라는 함수로 표현할 수 있는데 S가 B(t)보다 작다면 권리를 행사하는 영역이고 반대로 S가 B(t)보다 크다면 옵션을 보유하는 영역이다. 이를 수식으로 표현하면 다음과 같다.
| (3) |
옵션을 행사하는 영역인 Ω1에서 옵션의 가치는 다음과 같이 간단하게 표현된다.
| (4) |
반대로 옵션을 보유하는 영역인 Ω2에서의 옵션의 가치를 구해야 한다. 이러한 Ω2에서는 다음과 같이 블랙-숄즈 방정식을 만족한다.
| (5) |
r은 무위험 이자율,σ는 기초자산의 변동성이다. 식 (6)을 쉽게 표현하기 위해 다음과 같이 P에 대한 미분 연산자 Λ를 정의한다.
| (6) |
경계함수인 B에 의존하지 않는 식으로 식 (4)와 식 (6)을 통합하면 다음과 같이 쓸 수 있다.
| (7) |
여기서 (S,t)가 ϕ(S,t) - P(S,t) = 0을 만족하면 (S,t) ∈ Ω1이며, 반대로 ΛP(S,t) = 0을 만족하면 (S,t) ∈ Ω2이다.
만기 시점인 T에서의 옵션 가치를 활용하여 가격 함수 P의 종결 조건을 설정할 수 있다
| (8) |
또한, 디리클레 경계 조건은 다음과 같다.
| (9) |
3.2 PINN
PINN은 심층 학습의 강력한 성능을 활용하면서 기본적인 물리 법칙을 네트워크 손실 함수에 직접 통합하는 방식으로 편미분방정식을 해결하는 새로운 접근 방식을 제시한다. PINN의 구조는 일반적으로 다층 신경망으로 구성되며, 입력층은 공간적 및 시간적 좌표를 수용하고, 출력층은 이러한 좌표에서 편미분방정식의 해를 제공한다. PINN의 독특한 특징은 신경망의 손실함수에 편미분방정식의 잔차(Residual)를 포함시키는 방식으로 물리 법칙을 직접 통합한다는 점이다. 이는 자동 미분을 사용하여 입력 좌표에 대한 네트워크 출력의 미분을 계산함으로써 이루어지며, 편미분방정식 잔차가 0이 되도록 학습한다. 경계 조건과 초기 조건도 손실함수에 추가하여 유사하게 통합되며, 이는 모델의 결과가 이러한 제약 조건을 준수하도록 조절한다.
본 논문에서 사용된 PINN 모델은 미국형 풋 옵션 가격 결정의 맥락에서 블랙-숄즈 PDE와 그에 따른 경계 조건이 신경망에 통합된다. 본 논문에서는 Tanh 함수를 활성화 함수로 활용하여 옵션 가격 모델의 충격과 불연속성을 처리한다.
Ⅳ. 학습방법
4.1 학습 데이터 생성
우리 모델의 구현에서는 PINN이 효과적으로 학습할 수 있도록 영역 Ω 내에서 세 가지 유형의 데이터를 사용한다.
1) 랜덤 데이터 χrand : 영역 Ω 전체에 균일하게 분포된 랜덤 데이터를 생성한다. 이 데이터 세트는 213개의 데이터로 랜덤한 샘플을 제공한다.
2) 불연속 처리 데이터 χshock : 행사가 K와 만기 T 근처에서 발생하는 충격을 정확하게 모델링하기 위해, 이 영역에 집중된 213개의 데이터를 생성한다. 데이터의 영역을 다음과 같이 정의 하였다: [0.99K, 1.01K] × [0.99T,T]. 이 데이터 분포는 PINN이 솔루션이 급격한 변화를 보이는 영역에 집중적으로 분포되어서 불연속점에서 모델의 정확성을 향상한다.
3) 격자 형태 데이터 χgrid : Ω 범위를 커버하는 128 × 128 균등한 격자점으로 구성된 데이터를 생성한다. 이 구조화된 그리드는 매 학습마다 Ω에서 데이터가 없는 곳이 없도록 설정한다.
위의 세 가지 데이터를 합산하여서 다음과 같은 편미분방정식을 위한 데이터를 생성하였다.
| (10) |
이와는 별개로 종결 및 경계 조건을 위한 데이터 또한 생성한다. PINN의 터미널 및 경계 조건을 강제하기 위해, 이러한 목적으로 각각 214개의 랜덤하게 분포된 데이터를 다음과 같이 생성한다.
| (11) |
이러한 종결 및 경계 조건의 데이터는 함숫값을 다루는 디리클레 조건을 계산할 때 사용되었다.
4.2 신경망 모형 설계
우리의 PINN 모델은 미국형 풋 옵션의 가격을 산정하는 데 있어 복잡성을 효과적으로 처리하도록 설계되었다. 이 신경망은 입력층, 출력층, 그리고 7개의 잔차 블록(Residual block)으로 구성된다. 각 잔차 블록과 입력층, 출력층 내의 모든 층에는 150개의 뉴런이 포함되어 있다.
모든 층에서 Tanh 함수를 활성화 함수로 사용하였다. Tanh는 함수의 이차 미분 가능성이 중요한 PINN 모델에서 ReLU보다 우수한 성능을 보였다. ReLU는 원점에서 미분 불가능하며 이는 PINN의 성능에 부정적인 영향을 미친다.
우리는 이 PINN 모델을 u(θ;S,t)로 표현할 것이며 우리의 목표는 미국형 옵션 P(S,t)를 u(θ;S,t)로 근사하는 것이다.
4.3 손실함수
손실함수는 PINN의 학습 과정의 중요한 구성 요소이며, 세 가지 부분으로 나뉜다: 편미분방정식 손실함수 LPDE, 경계 조건 손실함수 Lbd, 그리고 종결 조건 손실함수 Lterm이 손실함수에 사용된 데이터는 앞서 언급된 χPDE, χlbd, χubd, χterm이다.
LPDE의 경우 식 (7)을 활용해서 다음과 같이 정의하는 것이 일반적이다.
| (12) |
다만 이러한 max의 경우 도함수에서 불연속성을 유발한다. 우리는 이 불연속성을 완화하기 위해서 기존의 max 함수 대신에 미분 가능한 다음과 같은 함수를 정의한다:
| (13) |
여기서 α는 maxα의 부드러운 정도를 나타내는 계수로 α값이 커지면 maxα는 max로 근사 된다. 이를 바탕으로 다음과 같이 기존 손실함수를 완화할 수 있다:
| (14) |
이와 마찬가지로 Lterm의 경우에도 식 (8)를 바탕으로
| (15) |
로 정의가 되는 것이 일반적이다.
하지만 ϕ(S,t) :=max(K - S,0)으로 미분 불가능한 함수이다. 우리는 이러한 ϕ를 완화해서 다음과 같이 ϕα를 Softplus 함수를 기반으로 정의한다.
| (16) |
이를 바탕으로 식 (15)을 다시 정의하면 다음과 같다:
| (17) |
경계 조건의 손실함수는 위 두 가지 경우와는 별개로 이미 미분 가능하다. 식 (10)을 활용하여서 정의하면 다음과 같다:
| (18) |
학습을 위해서 사용되는 총 손실함수 Ltrain은 다음과 같이 정의된다.
| (19) |
우리의 실험에서는 λPDE = 1, 그리고 그 외의 상수 λtrem,λbd = 0.1로 설정하였다.
이렇듯 손실함수를 미분 가능하도록 정의하여, PINN은 물리 법칙과 경계 조건을 준수하면서도 수치적으로 안정적이게 미국형 풋 옵션 가격 모델의 복잡한 가치를 보다 효과적으로 학습할 수 있다.
4.4 학습 과정
미국형 풋 옵션 가격을 위한 PINN의 학습 과정에서 우리는 Adam 최적화 방법론을 사용했다. 초기 학습률은 0.001로 설정되었다. 또한, 학습의 수렴을 보장하고 학습 과정을 미세 조정하기 위해 학습률 감소 전략을 구현했다. 구체적으로, 학습률은 4000 에포크마다 0.3의 비율로 감소했다. 전체 학습 과정은 10,000 에포크로 구성되었으며 각 에포크 동안 모든 데이터가 배치를 사용하지 않고 한 번에 사용되었다. 함수를 완화 시키기 위한 상수 α는 50으로 고정되었다.
V. 실험 결과
5.1 출력값
우리는 PINN의 성능을 벤치 마크하기 위해 BTCS(Backward Time Central Space) 유한 차분법과 이항 방법으로 얻은 옵션 가격 결과와 비교했다. 유한 차분법에서는 1000×1000 그리드를 사용했고, 이항 방법에서는 N=10000 단계를 사용했다. 모든 설정에서 행사가 K=100, 초기 주가 S=100, 만기 t=1년으로 설정되었다.
우리 모델은 앞서 언급된 모든 데이터 샘플링 방법을 사용하고, 모든 손실함수는 완화하여 미분 가능한 손실함수를 사용했다. 다양한 변동성 σ와 이자율 r 설정에 대한 P(S,0) 근사값 비교 결과는 표 1에 정리 하였다. PINN은 강력한 성능을 보여주었으며, 다양한 시나리오에서 정확한 가격 추정치를 생성했다. 비교 분석 결과, PINN의 가격 정확도가 전통적인 방법과 동등하며, 약간의 편차는 허용 가능한 범위 내에 있음을 보여주었다.
예를 들어, σ=0.2 및 r=0.1의 경우, PINN은 4.824의 가격 추정치를 제공하여, BTCS 결과인 4.852와 이항 결과인 4.816에 매우 근접한 결과를 보였다.
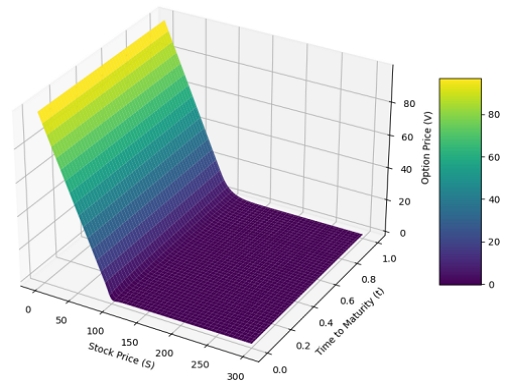
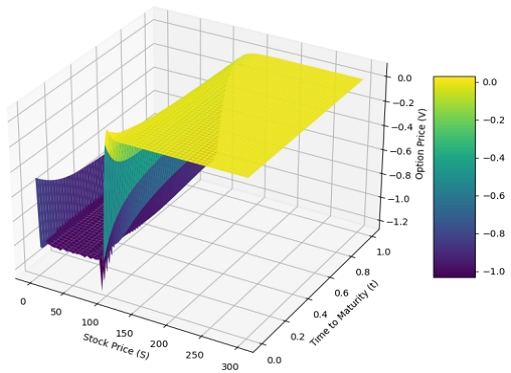
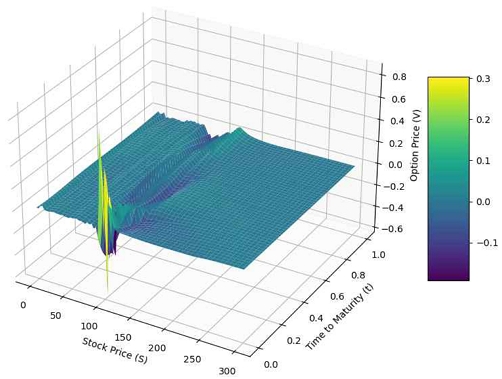
그림 1과 그림 2는 각각 옵션 가격의 근사값 u와 그 기울기에 대한 모델 출력값을 보여준다. 그림에서 보듯 PINN 모델의 정확성과 미분 가능성을 보여준다. 그림 2를 보면 행사가격 K 근처에서 쇼크가 생겼지만 크지 않은 것을 확인 할 수 있다.
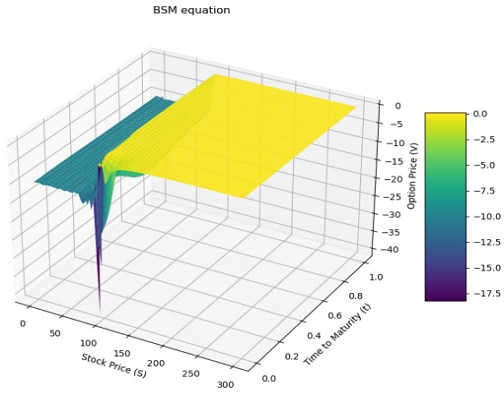
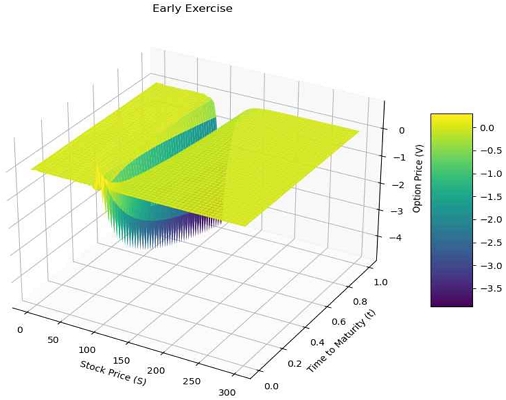
그림 3과 그림 4는 각각 블랙-숄즈 방정식의 잔차인 Λu와 ϕ - u의 3차원 그래프이다. 이론적으로는 부등식 Λu,ϕ - u≤0이 성립하므로, 두 그래프 모두 양의 값이 나타나지 않을 것이다. 실제로 그림 3과 그림 4에서는 모두 0 혹은 음의 값이 나타남을 알 수 있다.
여기서 그림 3에서 Λu=0으로 표현된 노란색 구역은 위에서 정의된 Ω2 이며 마찬가지로 초록색으로 칠해진 영역은 Λu<0인 구간으로 Ω1이다. 이러한 영역은 그림 4에서도 나타나지만 S가 커짐에 따라서 ϕ - u의 값도 0에 근사하기에 그림 3과 같이 명확하게 표현되지 않았다.
그림 5에서는 max(Λu(S,t),ϕ - u)의 값으로 우리가 LPDE를 통해서 학습하려고 한 잔차를 나타낸다. 식 (14)에서 보이듯 max(Λu(S,t),ϕ - u)의 값이 0으로 학습을 진행하였다. 실제로 그림 5에서는 대체로 0에 가까운 양상을 보인다. (K,T) 근방에서 쇼크가 보여지지만 이 영역에 집중된 데이터의 영향으로 쇼크의 크기가 1을 넘지 않는다.
5.2 방법론에 대한 제거 연구
우리 모델의 다양한 구성 요소의 기여도를 더 잘 이해하기 위해, 함수의 미분 가능성과 충격 영역 근처의 데이터 존재의 영향을 중점으로 제거 연구를 수행했다. 이 연구는 각 방법을 체계적으로 제거하고 모델의 성능 변화를 관찰했다.
우리는 모든 설정에서 K=100, S=100, T=1, σ=0.2, r=0.1년으로 설정하고 u(S,0)의 값을 계산하였다.
제거 연구는 우리 모델의 각 구성 요소의 중요성을 보여준다. 손실함수를 기존의 미분 불가능한 함수로 사용하면 옵션 가격이 4.789로 떨어지며, 이는 PDE 손실함수에서 미분 가능성의 중요성을 강조한다. 유사하게, 충격 영역 근처의 데이터를 제외하면 가격이 4.764로 감소하여, 옵션 가격 역학을 정확하게 포착하는 데 있어 목표 데이터 샘플링의 중요성을 강조한다. 미분 불가능한 손실함수를 사용하고 충격 데이터를 모두 제거하면 성능이 5.193으로 유한 차분법과 크게 차이가 난다.
표 2의 결과는 미분 가능성과 전략적으로 샘플링된 데이터가 미국형 풋 옵션 가격 산정에서 최적의 성능을 달성하는 데 필요함을 보여준다.
5.3 계산 시간
결과의 정확성 외에도 각 방법의 계산 시간을 측정했다. 이항법은 약 1.972초가 소요되었고, BTCS 방법은 4.901초가 필요했다. 우리의 PINN 모델은 단일 GTX 3090 GPU를 사용하여 학습하는 데 48분 59초가 소요되었다. 그러나 한 번 학습된 후, PINN 모델의 추론 시간은 훨씬 빨라서 0.0029초만 소요되었다. 이는 학습 단계가 완료된 후 PINN 모델이 실시간 적용에 매우 효율적임을 보여준다.
5.4 손실값 비교
PINN을 활용한 미국형 옵션 가격 결정 연구에서 Gatta의 논문은 옵션의 행사 여부를 구분하는 자유 경계 B(t)의 결정에 중점을 두고 있다. 따라서 Gatta의 연구에서는 옵션 가격 평가 결과가 아닌 최종 손실값을 기준으로 PINN 모델의 정확도를 판단했다. 공정한 비교를 위하여 우리 모델에 대한 손실값을 비교한다.
우리 모델에 대한 손실값을 표 3에 정리했다. Gatta의 결과와 유사하게 Lbd의 값은 LPDE와 Lterm보다 작다. 네 번의 실험에서 평균적으로 손실값은 0.011이다. 이는 Gatta의 논문에서 보고된 일차원 실험값 0.001189보다 높아 보이지만, 우리의 모델은 10배 높은 K값을 사용했음을 고려해야 한다. Mean Squared Error의 특성을 고려할 때, 우리의 손실값을 0.00011로 조정하여 비교하는 것이 타당하다.
우리의 학습은 약 80,000개의 데이터를 사용하였으며, 훈련에 사용한 에포크 수는 10,000회로, 30,000개의 데이터와 4,000번의 에포크를 사용한 Gatta의 연구보다 계산량이 많다. 그럼에도 불구하고, 우리의 모델은 10배 가까이 낮은 손실값을 기록하였다. 이는 우리의 모델이 경쟁력이 있음을 시사한다.
Ⅵ. 결 론
본 연구에서는 PINN을 미국형 풋 옵션 평가에 적용하는 방법을 탐구했다. 다양한 데이터 샘플링 방법을 사용하여 모델을 학습하고, 안정성과 정확성을 높이기 위해 PDE 및 종결 조건 손실함수를 미분 가능한 함수로 수정했다. 모델은 BTCS 유한 차분법 및 이항 방법과 같은 전통적인 수치 방법과 비교하여 다양한 시나리오에서 강력한 성능과 정확한 가격 결과를 보여주었다.
우리의 결과는 PINN 모델이 미국형 풋 옵션의 복잡한 동역학을 효과적으로 포착하며, 옵션 가격이 벤치마크 방법으로 얻은 것과 거의 일치함을 보여준다. 제거 연구는 손실함수의 미분 가능성과 충격 영역 근처의 목표 데이터 샘플링이 모델의 전체 정확성에 기여하는 중요성을 강조했다.
또한, 우리의 PINN 모델은 확장 가능성이 크다. 주가 S와 시간 t뿐만 아니라 변동성 σ, 행사가 K, 이자율 r등의 입력을 수용하도록 확장될 수 있다. 이 유연성은 모델을 다양한 금융 모델링 시나리오에 적합하게 만든다. 또한, 이 모델은 다차원 사례, 예를 들어 다중 자산 미국형 옵션을 처리하도록 쉽게 확장할 수 있어 금융 공학 분야에서의 적용 가능성을 넓힌다.
결론적으로, 우리의 연구는 PINN의 적응성과 효율성이 전통적인 수치 방법에 비해 비슷하지만 유연한 접근 방식을 제공한다. 향후 연구는 이 방법론의 추가 확장 및 응용을 탐구하여 더 강력하고 일반적인 모델을 제공을 목표로 한다.
References
-
H. S. Lee and S. H. Oh, "LSTM-based Deep Learning for Time Series Forecasting: The Case of Corporate Credit Score Prediction", The Journal of Information Systems, Vol. 29, No. 1, pp. 241-265, Mar. 2020.
[https://doi.org/10.5859/KAIS.2020.29.1.241]

-
M. Raissi, P. Perdikaris, and G. E. Karniadakis, "Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations", Journal of Computational Physics, Vol. 378, pp. 686-707, Feb. 2019.
[https://doi.org/10.1016/j.jcp.2018.10.045]

-
M. J. Brennan and E. S. Schwartz, "The Valuation of American Put Options", The Journal of Finance, Vol 32, No. 2, pp. 449-462, May 1977.
[https://doi.org/10.2307/2326779]

-
B. F. Nielsen, O. Skavhaug, and A. Tveito, "Penalty and front-fixing methods for the numerical solution of American option problems", Journal of Computational Finance, Vol 5, No. 4, pp. 69-97, Aug. 2002.
[https://doi.org/10.21314/JCF.2002.084]

-
K. Muthuraman, "A moving boundary approach to American option pricing", Journal of Economic Dynamics and Control, Vol 32, No. 11, pp. 3520-3537, Nov. 2008.
[https://doi.org/10.1016/j.jedc.2007.12.007]

-
A. Chockalingam and K. Muthuraman, "An approximate moving boundary method for American option pricing", European journal of operational research, Vol 240, No. 2, pp. 431-438, Jan. 2015.
[https://doi.org/10.1016/j.ejor.2014.07.031]

-
S. P. Zhu, "An exact and explicit solution for the valuation of American put options", Quantitative Finance, Vol. 6, No. 3, pp. 229-242, Feb. 2006.
[https://doi.org/10.1080/14697680600699811]

-
F. Gatta, V. S. D. Cola, F. Giampaolo, F. Piccialli, and S. Cuomo, "Meshless methods for American option pricing through physics-informed neural networks", Engineering Analysis with Boundary Elements, Vol. 151, pp. 68-82, Jun. 2023.
[https://doi.org/10.1016/j.enganabound.2023.02.040]

-
M. Kim, H. Jung, and C. Min, "Data Augmentation and Transfer Learning for Personal Credit Evaluation Model", The Journal of Korean Institute of Information Technology, Vol. 22, No. 3, pp. 11-21, Mar. 2024.
[https://doi.org/10.14801/jkiit.2024.22.3.11]

-
Z. Mao and X. Meng, "Physics-informed neural networks with residual/gradient-based adaptive sampling methods for solving partial differential equations with sharp solutions", Applied Mathematics and Mechanics, Vol. 44, No. 7, Jul. 2023.
[https://doi.org/10.1007/s10483-023-2994-7]

-
Z. Gao, L. Yan, and T. Zhou, "Failure-informed adaptive samping for PINNs", SIAM Journal on Scientiric Computing, Vol. 45, No. 4, 2023
[https://doi.org/10.1137/22M1527763]

-
Y. Bai, T. Chaolu, and S. Bilige, "The application of improved physics-informed neural network(IPINN) method in finance", Nonlinear Dynamics, Vol. 107, No. 4, pp. 3655-3667, Mar. 2022.
[https://doi.org/10.1007/s11071-021-07146-z]

-
X. Wang, J. Li, and J. Li, "A Deep Learning Based Numerical PDE Method for Option Pricing", Computational Economics, Vol. 62, No. 1, pp. 149-164, Jun. 2023.
[https://doi.org/10.1007/s10614-022-10279-x]

-
R. U. Seydel, "Tools for computational finance", Springer, Mar. 2012.
[https://doi.org/10.1007/978-1-4471-2993-6]

-
A. Dhiman and Y. Hu, "Physics Informed Neural Network for Option Pricing", arXiv preprint arXiv:2312.06711, , Dec. 2023.
[https://doi.org/10.48550/arXiv.2312.06711]


2022년 : 아주대학교 금융공학과(학사)
2022년 ~ 현재 : 아주대학교 금융공학과 석사과정
관심분야 : 옵션 평가, 딥러닝

2014년 : 서울대학교 수학과(학사)
2018년 : 서울대학교 수학과(석박사통합)
2020년 ~ 현재 : 아주대학교 금융공학과 교수
관심분야 : 비선형 동역학, 확률적 동역학