클래스 불균형 데이터 분류 예측을 위한 클러스터 기반 언더샘플링 기법
초록
신용카드 사기 탐지나 장애 탐지 등 일반적이지 않은 이상 탐지 분야에서는 다수클래스와 소수클래스가 불균형하게 분포하며 분류예측 성능에 많은 오류를 야기한다. 이를 해결하기 위한 데이터 조정 접근 방식 중 샘플링에 관한 연구가 활발히 진행 되어왔으며 많은 성과를 이루었다. 본 논문에서는 Kullback-Leibler Divergence을 활용하여 다수클래스의 모집단 분포를 반영하는 Cluster 기반 언더샘플링 방법을 제안한다. 이 방법은 다수클래스 데이터와 확률분포가 가장 유사한 샘플을 추출함으로써 언더샘플링의 주요 단점인 정보손실을 최소화한다. 본 연구에서는 불균형 비, 샘플 수, 특성 수 등에 대한 다양한 조건에서 실험을 진행하여 제안하는 언더샘플링 기법이 기존의 방법에 비해 성능이 향상되었음을 입증하였다.
Abstract
In the field of anomaly detection, specific cases such as credit card fraud detection and failure detection often have unevenly distributed major and minor classes that can lead to substantial errors in classification prediction performance. To address this issue, researchers have actively pursued data-level approaches such as sampling, resulting in many achievements. This study proposes a cluster-based undersampling method that reflects the distribution of the majority class population using Kullback-Leibler Divergence. This method minimizes information loss, a major drawback of undersampling, by extracting samples that are most similar to the probability distribution of the majority class data. In this study, experiments were conducted under various conditions such as class imbalance, sample size, and feature dimensions to demonstrate that the proposed undersampling technique outperformed the existing methodology.
Keywords:
imbalaced data, undersampling, cluster, kullback-leibler divergenceⅠ. 서 론
최근 데이터 저장 기법의 비약적인 발달과 처리비용의 감소에 힘입어 머신러닝에 기반을 둔 분류예측모형이 많이 활용되고 있다. 하지만 데이터의 규모가 방대해지면서 데이터에 내재된 분포가 복잡해지고 많은 노이즈를 포함하는 등 예측 모형의 성능을 저하시키는 문제점도 많이 발생하고 있다. 특히 데이터 클래스 간 불균형 현상은 가장 흔하게 접하는 문제로써 주로 신용카드 사기 탐지나 의료 진단, 장애 탐지 분야에서 많이 발생한다.
의사결정모형이나 신경망모형 등 대부분의 기계학습 알고리즘은 데이터의 클래스 간 비율이 비슷하다는 가정을 전제로 하지만 현업에서 발생하는 많은 분류예측 문제에서는 관심 대상이 되는 클래스의 비율이 매우 낮다[1]. 일반적으로 데이터의 불균형 상황에서 학습된 모형은 성능이 저하될 수 있기 때문에, 이를 극복하기 위한 다양한 기법들이 연구되고 있다[1]-[6].
데이터의 불균형으로 인한 문제는 크게 두 가지 접근법으로 해결한다. 첫 번째로 알고리즘 수준(Algorithm-level-approach)방법은 기존 기계학습 알고리즘의 오차함수를 수정, 비용개념을 사용해 소수클래스에 더 큰 중요도를 주어 성능을 높이는 방식을 취한다. 이는 우수한 품질의 데이터가 이미 확보되어 있다는 가정 하에 분류모형 선택이나 하이퍼파라미터 튜닝, 최적화 기술 등에 중점을 둔다. 두 번째로 데이터 수준 방법(Data-level-approach)은 데이터의 일부를 제거하거나 증폭시켜 데이터의 불균형성을 해소한다. 소수클래스(Minor class)의 데이터를 다수클래스(Major class)만큼 증가시키는 오버샘플링(Oversampling), 다수클래스를 소수클래스만큼 감소시키는 언더샘플링(Undersampling), 그리고 이들을 결합한 방식인 앙상블(Ensemble) 방법으로 나누어진다. 이러한 접근법은 불균형 데이터에 대한 직접적인 처리를 통해 분류 모형의 고도화 이전 단계에서 일차적으로 데이터 불균형 문제를 해결할 수 있기 때문에 많은 노이즈를 포함한 현실 데이터에 빠르게 적용할 수 있다는 장점이 있다. 본 연구에서는 불균형성 해결을 위한 데이터 수준 방법을 다룬다.
불균형 데이터의 특징을 두 가지로 나눠보면 첫째는 소수클래스의 데이터가 다수클래스에 비해 상대적으로 매우 적은 경우이고 둘째는 소수클래스 데이터 자체가 절대적으로 덜 확보된 경우다. 다행히 방대한 데이터 수집이 가능해지면서 극단적 불균형 데이터라 할지라도 소수클래스 데이터 절대량이 확보되어 있는 첫 번째 경우가 대부분이다. 이 경우 오버샘플링은 빅데이터 처리를 위한 처리시간과 저장공간 등 경제적 비용이 발생한다. 따라서 본 연구에서는 언더샘플링을 활용하여 데이터 불균형 문제를 해결하는데 초점을 맞추고자 한다.
전통적인 언더샘플링 방법은 데이터 불균형으로 인해 편향된 다수클래스와 소수클래스 간 분류경계를 조정하는 방식인데, 이는 데이터 제거로 인한 정보손실과 샘플 크기 선택을 위한 자유도의 한계가 있었다. 이에 본 논문에서는 다수클래스의 정보력을 잃지 않으면서 분류예측 성능을 향상 시킬 수 있는 클러스터(Cluster)기반의 최적 언더샘플링 방법을 제안하고자 한다. 다수 클래스의 정보를 보존하는 샘플링을 위해 쿨백-라이블러 발산(KLD, Kullback-Leibler Divergence) 함수를 추출된 샘플과 모집단과의 유사성 검증 지표로 활용한다. 다양한 조건의 시뮬레이션을 퉁해 기존 샘플링 방법과 비교 실험하였고 본 연구가 제안하는 방법의 분류예측 성능이 더 우수함을 입증한다.
본 논문의 구성은 다음과 같다 2장에서는 관련 연구를 조사 분석하고 3장에서는 제안하는 샘플링 기법과 검증 지표에 대해 상세히 기술한다. 4장에서는 실험을 통해 기존 연구와 성능 비교를 실시하고 제안방법론의 우수성을 보인다. 마지막으로 5장에서는 결론 및 향후 연구를 설명한다.
Ⅱ. 관련 연구
2.1 분류 경계면을 조정하는 언더샘플링
언더 샘플링이란 다수클래스를 삭제하여 클래스간 분류 경계면을 조정하는 방법으로 다수클래스를 소수클래스의 수에 맞도록 데이터 비중을 조절한 뒤 모델링에 활용하는 방법이다.
이때 데이터 삭제로 인한 정보손실이 발생하기 때문에 이를 최소화하고 예측 성능을 향상시키기 위한 다양한 언더샘플링이 제안되었다.
P. E. Hart(1968)에 의해 제시된 CNN(Condenced Nearest Neibour)는 무작위로 다수클래스를 제거하는 RUS(Random Under Sampling)와는 달리 다수클래스 데이터 포인트와 가장 가까운 데이터가 소수클래스가 아니면 모두 삭제하는 방법이다 두 클래스의 경계가 명확할 때 경계 부분 데이터만 남겨 최소한의 부분집합을 찾는 게 목적인 샘플링 방법으로 데이터 축소 효과가 크다. 다만 표본의 숫자가 커지면 시간이 많이 걸리는 단점이 있다[7].
D. L. Wilson(1972)에 의해 제시된 ENN(Editetd Nearest Neighbours)방법론은 이상치와 결정 경계의 데이터를 제거 할 수 있는 방법이다. 다수클래스 포인트를 기준으로 KNN을 적용하는데 일반적으로 k=3을 사용하게 된다. 소수클래스의 자료가 굉장히 적은 경우 제거되는 다수클래스의 자료가 거의 없을 수 있다[8]. 그 다음으로 I. Tomek이 1976년 발표한 리샘플링된 데이터의 집합의 변화가 없을 때까지 ENN을 반복적으로 수행하는 방식인 Repeated ENN(RENN)과 ENN을 변형한 방식으로 k값을 설정하여 1 ≤ i ≤ k 범위의 모든 i-NN을 수행하는 ALL_KNN 이 있다[9]. J. Laurikkala(2001) 에 의해 제시된 NCR(Neighborhood Cleaning Rule)은 두 단계를 거치는데 ENN을 통해 일부 다수클래스를 제거한 뒤 소수클래스를 기준으로 KNN(k=3)을 수행했을떄 2개이상의 자료가 다수클래스로 분류되는 경우 다수클래스를 삭제한다. 다만 ENN과 마찬가지로 소수클래스의 수가 굉장히 적거나 클래스간 데이터 중첩이 적은 경우 많은 데이터를 제거할 수 없다[10].
TL(Tomek’s Link)는 불균형 자료의 이상치와 결정 경계의 자료를 제거하기 위한 방법으로 I. Tomek(1976)에 의해 제시되었다. 먼저 Tomek’s link란 서로 다른 클래스를 갖는 두 개의 표본 (xi,xj)의 거리가 d(xi,xk) < d(xi,xj) 또는 d(xk,xj) < d(xi,xj)으로 성립하는 xk 가 존재하지 않을 때 (xi,xj)를 의미한다. 먼저 전체 자료에서 Tomek’s link가 성립하는 자료들을 찾은 뒤 해당 자료 중 다수클래스의 자료를 제거하여 샘플링 하는 방법이다[11]. 다음은 K. Miroslav and S. Matwin(1997)에 의해 고안된 OSS(One Side Selection)이다. 이 방법은 Tomek’s link를 수행한 뒤 추가로 CNN을 수행한다. 구체적으로는 중복된 데이터를 제거하는 방법으로 CNN을 사용하고 이후 노이즈 데이터와 결정 경계 근처 데이터를 제거하는 방법으로 Tomek’s link를 사용하는 방식이다[12].
I. Mani(2003)의 NearMiss-1 방법은 다수 클래스 데이터 포인트와 가장 가까운 소수 클래스 데이터 3개 와의 평균 거리를 계산하고 평균 거리가 가장 작은 데이터를 비율에 맞게 남기고 그 외에는 삭제하는 방법이다. NearMiss-2 방법은 NearMiss-1과는 반대로 가장 먼 데이터를 3개 뽑도록 변형한 방식이며, NearMiss-3 는 NearMiss-1 방법과 동일하게 작동하지만 소수클래스 데이터 N개를 사용자가 지정해 주는 방법이다[13].
마지막은 RUS(Random Under Sampling)방법으로 다수 클래스 데이터를 소수 클래스 수 만큼 샘플링하는 방법이다.
2.2 모집단의 특성을 반영하는 언더샘플링
2017년 W.-C. Lin은 k-means 알고리즘을 사용하여 다수클래스의 데이터를 소수클래스 데이터 만큼 군집화하고 군집의 평균값을 다수클래스의 데이터로 대체시키는 군집화 기반 언더샘플링(이하 k-means*)을 제안하였다. 이 방법은 다수클래스의 특징을 잘 나타내는 데이터를 골고루 추출할 수 있는 장점이 있다[14]. 그러나 실제 데이터가 아닐 수 있는 군집의 평균값을 대표 데이터로 사용하기 때문에 정보의 왜곡이 발생할 수 있다. 이를 해결하기 위한 방법으로 군집의 중심을 실제 데이터로 대체하는 언더샘플링(이하 k-medois*) 알고리즘을 사용하여 기존의 k-means를 사용한 언더샘플링의 단점을 극복하였다[15].
2023년 두 단계로 구성된 접근 방식을 활용한 불균형 데이터의 클러스터 기반 언더 샘플링 방법이 제안되었다[16]. 이 방법의 주요 특징은 첫 번째 단계에서 클러스터링 기법을 사용하여 다수 클래스의 샘플을 클러스터로 분할하고, 두 번째 단계에서는 언더 샘플링을 통해 각 클러스터에서 소수클래스 샘플을 제거하는 방식이다.
이렇게 함으로써 데이터의 불균형을 줄이고 분류 모델의 성능을 향상 시킬 수 있다고 한다. 다만 성능검증에 활용한 데이터의 수가 129에서 5,472개로 다소 적어 본 연구에서 직접 비교하지는 않는다.
기존의 언더샘플링 연구 방법은 대부분 분류예측 성능을 높이기 위해 다양한 알고리즘을 활용하고 데이터를 축약하는 것에 중심을 두고 진행되어왔다. 샘플링된 데이터가 전체 모집단을 대표한다고 주장할 수 있는 검증단계가 없었으므로 테스트 데이터를 통해서만 성능 확인이 가능했던 것이 사실이다. 이에 검증단계를 추가한 연구(2019)가 발표되었으며 내용은 다음과 같다. 다수클래스 데이터에서 서로 겹치지 않도록 소수클래스 데이터과 같은 수의 데이터①을 랜덤언더샘플링(이하 RUS*)으로 추출한다. 이를 제외한 나머지 다수클래스 데이터를 균등하게 두 개로 나누고 이 중 한 개의 데이터만 사용하여 새로 라벨링 후 분류모델을 생성한다. 이후 데이터①과 사용하지 않은 나머지 데이터를 정확히 구분할 수 있는지 성능을 검증한다. 랜덤 확률 0.5 근처에서 측정된다면 데이터는 차이가 없다고 간주하고 데이터①을 최종샘플로 결정하게 된다[17].
2.3 두 집단의 분포 유사성 검증 지표
두 분포의 차이를 나타내는 지표이며 샘플링 전후의 데이터 유사성을 검증하는 값으로 쿨백-라이블러 발산을 사용하고자 한다.
확률분포 P가 있을 때 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우의 엔트로피(정보량) 변화가 생긴다. 따라서, 원래의 분포가 갖는 엔트로피 H(P)와 P 대신 Q를 사용할 때의 교차엔트로피 H(P,Q)의 차이를 구하면 식 (1)과 같다.
| (1) |
위의 식을 정리한다면 앞서 밝힌 쿨백-라이블러 발산의 정의인 식 (2)가 유도된다.
| (2) |
결론적으로 쿨백-라이블러 발산 값은 모집단과 샘플데이터 두 분포의 차이를 나타내는 지표로 활용 가능하다.
Ⅲ. 연구방법
3.1 CSSMC 언더샘플링 기법 제안
기존의 언더샘플링 기법은 다수클래스와 소수클래스 분포에 따라 데이터 축약의 효과가 미미한 경우가 많이 있었다. 따라서 본 연구에서는 다수클래스 데이터를 축약하여 데이터 분석에 소요되는 시간과 비용을 줄이면서 분류성능을 높게 하는 언더샘플링인 CSSMC(Cluster Subset Similar to the Major Class)를 제안하고자 한다. 특히 정보손실을 최소화하고 불균형 데이터의 분류예측 성능을 높이는데 우수한 방법인 클러스터 기반의 알고리즘을 진행하고 각 군집에서 층화추출법(Stratified random sampling)으로 샘플링하여 표본의 대표성을 향상시키고자 한다.
분석 시간을 줄이기 위해서는 도출된 샘플이 최종 테스트 데이터를 통한 성능평가 단계 이전에 높은 확률로 모집단을 대표한다고 판단 할 수 있어야 한다. 따라서 샘플의 분포가 다수클래스의 분포를 잘 축약하는지를 판단하는 유사성 검증을 제안한다.
도메인 특성에 따라 적합한 샘플링 방법론은 현실적으로 모두 다르기 때문에 실험을 통해 매번 적합성을 확인하는 것은 시간 낭비이다. 유사성 검증을 통해 검토 시간을 감소시켜 빠른 모델 적합이 가능할 수 있게 하고, 이를 위해 두 데이터 집단의 확률분포 차이를 계산하는 함수인 쿨백-라이블러 발산 값을 분포유사도 개념으로 사용한다.
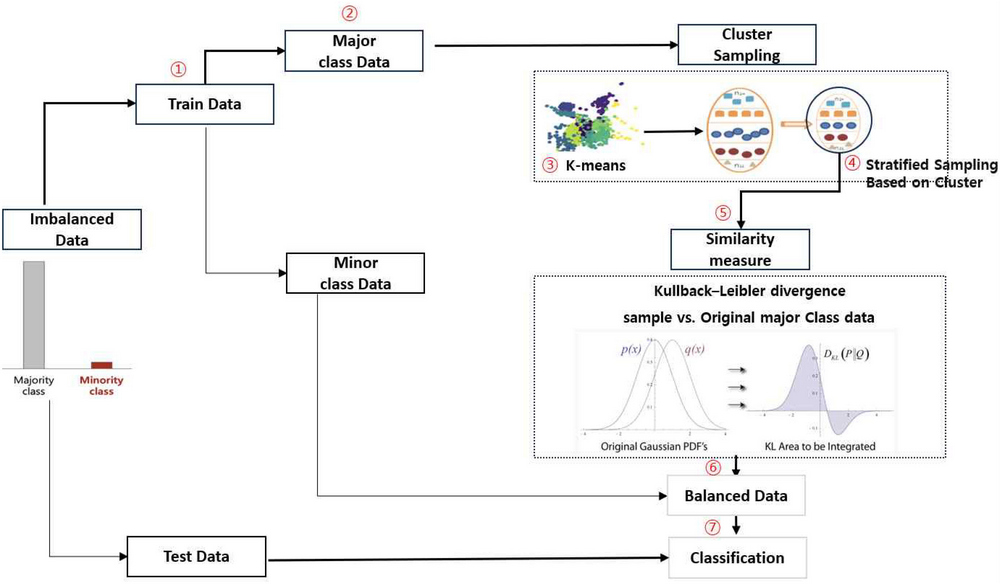
표본의 대표성 여부 쿨백-라이블러 발산값으로 검증하게 될 것이다. 그림 1은 샘플링 기법을 포함하여 성능검증까지의 단계별 프로세스를 도식화하여 그린 그림이다. 그림 1의 CSSMC 방법론의 단계별 내용은 다음과 같다.
- (1) Original 불균형 데이터에서 train 데이터를 분리하고 이 중 다수클래스(y=0) 만으로 k-means cluster를 수행한다. (①-③)
- (2) (1)에서 얻어진 cluster를 기준으로 층화추출 샘플링을 진행하여 여러 subset을 얻는다. (④)
- (3) (2)의 subset 중 train 데이터의 쿨백-라이블러 발산 값을 계산하고 가장 작은 값을 갖는 subset을 최종 샘플로 결정한다. (⑤)
- (4) 소수클래스 데이터와 (3)으로부터 얻은 최종 샘플을 결합하여 균형데이터를 만든다 (⑥)
- (5) 분류모델에 적합시킨 후 Test 데이터를 통해 성능을 평가한다. (⑦)
3.2 성능 비교를 위한 분류모델
데이터의 불균형이 심할수록 신경망모형보다 머신러닝모형의 예측력이 더 높다는 것은 여러 연구에서 증명된 바가 있다. 이에 본 연구에서는 예측력을 높이고자 LightGBM을 분류예측 성능 평가 모델로 사용하고자 한다. 여러 의사결정나무(tree)를 부스팅 방법을 통해 결합한 XGBoost의 시간적 한계를 보완하기 위해 나온 LightGBM은, 항상 트리의 균형을 맞추어 분기하는 level-wise(균형 트리 분할)를 사용하는 기존 알고리즘과는 다르게 leaf-wise(리프 중심 트리 분할)를 채택한다. 즉 트리의 균형을 맞추지 않고 최대 손실값을 가지는 리프 노드를 지속적으로 분할해서 트리를 생성할 수 있다. 이렇게 생성된 규칙 트리는 학습을 반복할수록 균형 트리 분할 방식보다 예측 오류를 최소화하며 더 작은 메모리를 사용, 학습 시간도 적게 걸린다. 즉 빠른계산속도와 높은 성능을 보장받을 수 있는 알고리즘이다. 다만 적은 데이터에 대해서는 과적합(Overfitting)이 일어나기 쉬운데, 여기서 적은 데이터의 기준은 1만건을 기준으로 한다고 알려져 있다. 성능평가를 위해 2/3는 train 데이터로 1/3은 test 데이터로 분할하고 Precision(정확도), Recall(재현율), F1 Score로 측정하였다. Precision과 Recall은 F1 Score가 같을 경우 참고하기 위함이며 최종적으로는 F1 Score를 기반으로 측정하였다. 각각의 식은 다음과 같다.
Ⅳ. 연구 결과
4.1 실험설계
본 절에서는 모의실험을 위한 다양한 조건의 불균형 데이터를 생성하고 모형에 적합한 뒤 CSSMC방법론과 기존 샘플링 방식의 성능을 비교할 것이다. 단계별 실험 과정은 다음과 같다.
- (1) 다변량 정규분포를 따르는X1, X2를 생성한다.
- (2) X1 데이터에 y=0을, X2데이터에 y=1 라벨링 후 결합하여 불균형 데이터를 만든다.
- (3) (2)를 7:3의 Train/Test 데이터로 분리한다.
- (4) (3)의 Train 데이터에서 기존 연구방법론을 사용하여 제안방법론과 비교할 샘플을 구성한다.
성능평가의 일반화를 위해 다양한 환경의 불균형 데이터를 반영하고자 표 1과 같이 조건을 통제하여 성능을 비교하였다.
4.2 성능 평가
표 2는 Train 데이터에서의 불균형 비율 1:10 하에서 feature 30개 생성 후 각 알고리즘대로 샘플을 추출하고 LightGBM을 사용하여 성능을 평가한 결과이다. 순서대로 1번부터 7번까지는 기존의 연구방법론이고 8~10번은 모집단 반영하는 언더샘플링, 마지막은 본 연구에서 제안하는 샘플링 방법이다.
우선 주목할 점은 3번 ENN부터 7번 RENN까지 RUS를 제외한 모든 언더샘플링 방법은 다수 클래스 모집단 축약 효과가 거의 없었다는 점이었다. 이는 KLD값이 아주 작게 산출된 이유이기도 하다.
ENN은 소수클래스 주변 다수 클래스를 삭제시키는 방식으로 클래스 경계에 있는 데이터에만 초점을 맞추기 때문에 불균형 데이터처럼 소수클래스가 상당히 적은 경우에는 데이터 축소 효과를 낼 수 없다. 또한 서로 다른 클래스에 속하는 인접한 샘플 쌍을 제거하여 데이터를 축소하는 Tomek’s link 방법은 샘플을 제외하기 이전보다 클래스 간 구분이 명확해지는 장점은 있으나 데이터 불균형 환경에서는 Tomek’s link로 묶이는 샘플 쌍의 조합이 한정적이므로 데이터의 실제 크기를 크게 축소하지 못한다. ENN과 Tomek’s link 두 개의 방법을 조합하거나 반복 수행하는 형태인 나머지 방식들도 마찬가지다.
기존 일반적인 언더샘플링 방식은 클래스 간 분류 경계면을 명확하게 하는 방식으로 작동하기에 불균형 데이터 환경 하에서는 언더샘플링 효과가 현저하게 떨어지는 한계가 있음을 보여준다. 본 연구의 목적인 불균형 환경하에서 언더샘플링 방법으로 CSSMC는 데이터 축소 효과와 분류예측 성능 면에서 모두 우수한 방법임을 알 수 있다. 이 결과는 feature의 수와 Cluster의 수준을 30으로 고정한 뒤 얻은 결과지만 다른 다양한 조건의 조합 수준에서도 비슷한 성능 패턴을 보였기에 이곳에서는 생략하기로 한다.
표 3은 Train 데이터의 불균형 비율 1:100 하에서 각 알고리즘별 샘플의 성능을 평가한 결과이다.
CSSMC사용 모형의 F1 Score는 샘플 크기 10,000 기준 0.60으로 앞서 실험한 1:10의 불균형 환경에서의 F1 Score값인 0.86보다는 작지만 다른 방법론과의 성능 차이가 더 뚜렷함을 확인할 수 있는데 이는 CSSMC방법론이 더 극단적인 불균형 환경하에서 안정적으로 작동한다는 것을 뜻한다. 기존 언더샘플링 방법론은 랜덤샘플링을 제외하고 데이터의 사이즈 감소 효과가 미미함을 다시 한번 확인 할 수 있었다. CNN은 수행시간이 오래 걸려 성능 측정이 어려웠으며 이는 관련 연구 부분에서 단점으로 언급된 내용이다.
4.3 데이터 형태에 따른 성능 비교
기존 언더샘플링 방법은 가장 중심으로 고려되어야 할 요소 중 하나인 다수 클래스 데이터 축약 효과가 거의 없었고 수행시간이 오래 걸려 제안하는 CSSMC 방법론과 직접 비교하는 것은 무리가 있었다. 따라서 소수 클래스만큼 다수 클래스를 군집화하고 그 군집의 중심점으로 다수 클래스 데이터를 대체하는 방법론과(K-means*, K-medois*), 훈련데이터와 모집단과의 유사성을 검증하는 방법론(RUS*)만을 가지고 본 논문에서 제안하는 언더샘플링 구성방식의 성능 비교를 추가로 진행하고자 한다. 앞선 실험에서 제안하는 방법론은 추출 샘플 크기에 관계 없이 성능이 가장 뛰어났으며 쿨백-라이블러 발산값 역시 비교 방법론 대비 작은 값으로 모집단을 더 잘 반영한다고 판단된다. 다만 Gaussian Mixture를 따르는 다수클래스와 소수클래스의 feature 간의 거리 차이를 유클리디안 거리(Euclidean dist)로 측정했을 때 그 값이 클수록 즉 다수클래스와 소수클래스의 분포가 다름이 분명하기에 분류 성능 F1 Score는 다른 요건의 변경과 관계 없이 정확도 1에 가까워지진다. 따라서 이를 통제하기 위해 4.1 실험설계 단계 (1)의 μ1 과 μ2 평균벡터의 거리는 3 이하로 통제했다.
앞선 실험설계는 샘플을 이루고 있는 모든 변수들을 수치형으로 구성하였으나 현실적으로 많은 분야에서 수치형 데이터와 범주형 데이터가 혼재되어 있기 때문에 이 경우 군집분석에서 주로 사용하는 K-means를 그대로 사용하는 방법은 범주형데이터의 정보를 손실할 수 있다.
따라서 수치형과 범주형 혼합 데이터에서의 분류 성능평가를 확인하는 실험을 추가하고자 한다. 혼합형 데이터를 다루는 군집 분석 시 거리를 계산 할 때 변수의 종류에 따라 사용할 수 있는 유사도 거리 중 본 논문에서는 K-prototype을 사용하였다. 수치형데이터는 K-means를 수행하고 범주형데이터는 K-mode를 사용하여 작동하는 방식이다. 실험을 위한 데이터는 기존 Train 데이터 구성 요소인 30개의 수치형 변수 중 일부와 0.7과 0.9 사이의 성공확률 p를 모수로 하는 이항분포에서 범주형변수 일부를 추출한 뒤 데이터를 결합하여 표 4와 같이 구성하고 성능을 살펴보았다.
CSSMC 방법은 주어진 환경에서 기존 방식보다 우위의 예측 성능을 보인다는 사실을 확인할 수 있다. 이는 해당 샘플과 다수 클래스 모집단과의 분포 차를 의미하는 KLD 값이 가장 작음을 통해서도 증명된다.
4.4 실증 데이터 분석
앞서 살펴본 CSSMC 방법을 실증데이터로 평가해 보고자 한다. 불균형 데이터를 가장 쉽게 접할 수 있는 카드사기 분야를 선택, kaggle의 ‘creditcard’ 데이터를 활용하였다. 이는 유럽 카드 소지자의 2013년 신용카드 거래를 포함하는 28만 건 이상의 레코드로 구성되어 있으며 카드 소지자의 개인정보를 보호하기 위해 익명화 처리되었다. 이 중 학습에 사용한 데이터는 정상 199,020, 사고 344개로 불균형비는 약 1:580이며 주요 변수는 다음과 같다.
알고리즘과 미세조정 등의 영향을 통제한 상황에서의 샘플링 성능을 평가하고자 하는 것이 목적이므로 앞서 시뮬레이션에서 활용한 LGB모형과 하이퍼파라미터를 동일하게 사용하였으며 CSSMC의 cluster와 샘플 수는 각각 15, 20,000으로 설정하였고 그 결과는 아래 표 6과 같다.
약 20만 샘플 수를 처리한 K-medoids 값은 메모리 문제로 얻을 수 없었다. 중앙값은 평균에 비해 이상치에 영향을 덜 받기 때문에 K-medoids 방법론은 K--means방법에 비해 안정적인 장점이 있으나 계산복잡도가 훨씬 높기에 속도가 상당히 느린 단점이 있다. 작은 데이터에서는 잘 작동하나 대규모 데이터를 다룰 때는 적절하지 않고 비용의 문제가 발생한다.
Ⅴ. 결론 및 향후 과제
본 연구에서는 머신러닝을 위한 불균형 데이터 처리 방법을 제안했다. 제안하는 기법은 샘플링 방법을 중심으로 다수 클래스의 모집단 분포를 잘 추출했는지를 검증하고 데이터 불균형으로부터 오는 오류를 최소화하려는 언더샘플링 방법이다.
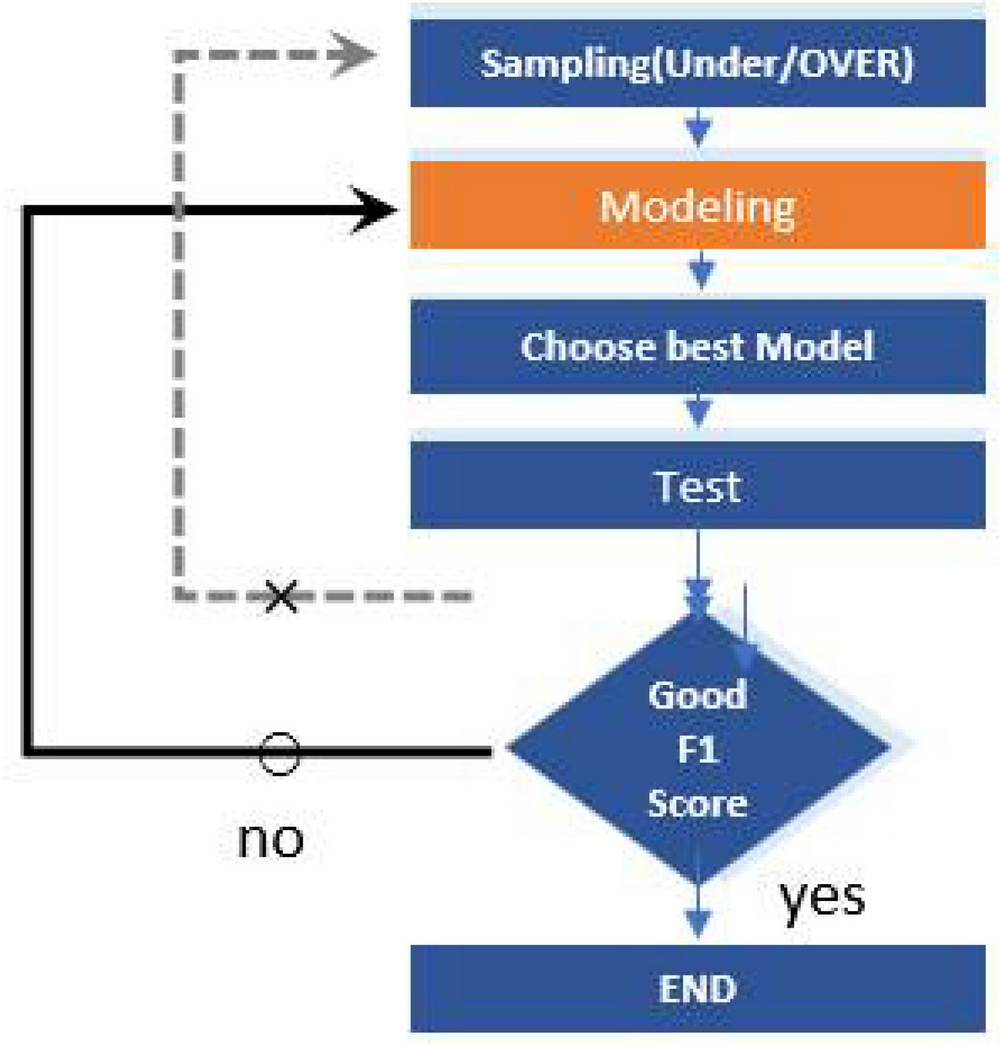
또한 기존 7개의 언더샘플링 방법론과 모집단을 잘 반영할 수 있도록 설계된 3개의 연구방법을 다양한 불균형 실험데이터 셋으로 성능평가를 진행한 결과 제안하는 CSSMC의 성능이 우수함을 확인할 수 있었다. 이러한 결과는 쿨백-라이블러 발산을 통해 샘플데이터와 모집단 분포의 유사도를 정량적으로 측정한 분석 결과라는 점에서 의의를 갖는다. 쿨백-라이블러 발산값은 모델 예측에 사용할 최종 샘플을 후보 샘플들 사이에서 선택하는데 판단 근거로 사용될 수 있는데 그림 2에서 표현했듯이 사전 검증 절차를 통해 샘플에 대한 확신을 가지고 모델 수정 등의 절차만 반복할 수 있으므로 만족할 만한 성능이 확보되지 않은 경우 샘플링부터 다시 해야 하는 번거로움을 줄여 줄 수 있다.
마지막으로 수치형과 범주형 데이터가 혼합된 데이터 환경에서도 제안하는 CSSMC 방법론 성능의 우수성이 입증되었다. 다만 범주형 변수가 전체 데이터에서 차지하는 비중이 커질수록 수치형 데이터로만 이루어진 샘플에 비해 예측 성능이 전반적으로 낮은 수치를 기록했다는 점 등에서 본 연구의 한계를 찾을 수 있다. 따라서 이들 한계점을 극복하기 위한 연구를 실제 데이터 검증을 추가하여 본 논문의 향후 과제로 한다.
References
- S. M. A. Elrahman and A. Abraham, "A review of class imbalance problem", Journal of Network and Innovative Computing, Vol. 1, pp. 332-340, 2013.
-
A. Singh and A. Purohit, "A survey on methods for solving data imbalance problem for classification", International Journal of Computer Applications, Vol. 127, No. 15, pp. 37-41, Oct. 2015.
[https://doi.org/10.5120/ijca2015906677]

-
J. L. Leevy, T. M. Khoshgoftaar, R. A. Bauder, and N. Seliya, "A survey on addressing high-class imbalance in big data", Journal of Big Data, Vol. 5, No. 42, pp. 1-30, Nov. 2018.
[https://doi.org/10.1186/s40537-018-0151-6]

-
Z. Zheng, X. Wu, and R. Srihari, "Feature selection for text categorization on imbalanced data", ACM Sigkdd Explorations Newsletter, Vol. 6, No. 1 , pp. 80-89, Jun. 2004.
[https://doi.org/10.1145/1007730.1007741]

-
P. Cao, D. Zhao, and O. R. Zaïane, "A PSO-based cost-sensitive neural network for imbalanced data classification", Proc. Pacific-Asia conference on knowledge discovery and data mining, Golden Coast, QLD, Australia, Vol. 7867, pp. 452-463, 2013.
[https://doi.org/10.1007/978-3-642-40319-4_39]

-
S. Picek, A. Heuser, A. Jovic, S. Bhasin, and F. Regazzoni, "The curse of class imbalance and conflicting metrics with machine learning for side-channel evaluations", Ruhr Universitat Bochum, Vol. 2019, No. 1, Nov. 2018.
[https://doi.org/10.13154/tches.v2019.i1.209-237]

- P. E. Hart, "The condensed nearest neighbor rule", IEEE Transactions on Information Theory, Vol. 14, No. 3, May 1968.
-
D. L. Wilson, "Asymptotic properties of nearest neighbor rules using edited data", IEEE Transactions on Systems, Man, and Cybernetics, Vol. SMC-2, No. 3, pp. 408-421, Jul. 1972.
[https://doi.org/10.1109/TSMC.1972.4309137]

-
I. Tomek, "An experiment with the edited nearest-neighbor rule", IEEE Transactions on systems, Man, and Cybernetics, Vol. SMC-6, No. 6, pp. 448-452, Jun. 1976.
[https://doi.org/10.1109/TSMC.1976.4309523]

-
J. Laurikkala, "Improving identification of difficult small classes by balancing class distribution", Proc. Conference on Artificial Intelligence in Medicine in Europe – Artificial Intelligence in Medicine, Cascais, Portugal, Vol. 2101, pp. 63-66, Jan. 2001.
[https://doi.org/10.1007/3-540-48229-6_9]

-
I. Tomek, "Two Modifications of CNN", IEEE Transactions on Systems, Man and Cybernetics, Vol. SMC-6, No. 11, pp. 769-772, Nov. 1976.
[https://doi.org/10.1109/TSMC.1976.4309452]

- K. Miroslav and S. Matwin, "Addressing the curse of imbalanced training sets: one-sided selection", Proc. International Conference on Machine Learning, Vol. 97, pp. 179-186, 1997.
- J. Zhang and I. Mani, "kNN approach to unbalanced data distributions: a case study involving information extraction", Proc. workshop on learning from imbalanced datasets, Vol. 126, 2003.
-
W.-C. Lin, C.-F. Tsai, Y.-H. Hu, and J.-S. Jhang, "Clustering-based under sampling in class imbalanced data", Information Sciences, Vol. 409-410, pp. 17-26, Oct. 2017.
[https://doi.org/10.1016/j.ins.2017.05.008]

- J. Oh and J. Baek, "Clustering-based Undersampling for Imbalanced Data Classification", Korean Institute of Industrial Engineers, Fall Conference Program, pp. 1910-1916, Nov. 2017.
-
A. Farshidvard, F. Hooshmand, and S. A. MirHassani, "A novel two-phase clustering-based under-sampling method for imbalanced classification problems", Expert Systems with Applications, Vol. 213, No. 2, Mar. 2023.
[https://doi.org/10.1016/j.eswa.2022.119003]

-
K. Lee, J. Lim, K. Bok, and J. Yoo, "Handling Method of Imbalance Data for Machine Learning: Focused on Sampling", Journal of the Korea Contents Association, Vol. 19, No. 11, pp. 567-577, Nov. 2019.
[https://doi.org/10.5392/JKCA.2019.19.11.567]

-
H. S. Lee, S. G. Hong, J. N. Bang, and H. J. Kim, "Study of Optimization Techniques to Apply Federated Learning on Class Imbalance Problems", Journal of KIIT, Vol. 19, No. 1, pp. 43-54, Jan. 2021.
[https://doi.org/10.14801/jkiit.2021.19.1.43]


2005년 2월 : 서울여자대학교 수학과(이학사)
2007년 2월 : 이화여자대학교 통계학과(이학석사)
2022년 3월 ~ 현재 : 국민대학교 데이터사이언스학과 박사과정
관심분야 : 머신러닝,빅데이터, 샘플링, FDS모델링

2003년 2월 : 연세대학교 경제학/응용통계학(경제학사)
2005년 2월 : 연세대학교 응용통계학(통계학석사)
2010년 8월 : Pennsylvania State University 통계학(통계학박사)
2013년 3월 ~ 현재 : 국민대학교 데이터사이언스학과 교수
관심분야 : 머신러닝, 딥러닝, 데이터마이닝