Bayesian neural network를 활용한 화재 오인식 개선 연구
초록
현재 딥러닝 모델들의 잘못된 예측으로 간혹 사고가 발생하고 있는 게 사실이다. 특히 화재 및 재난의 경우에는 피해 규모는 상상을 초월할 수 있다. 본 논문에서는 화재와 같이 Data 수집이 제한되었을 때 화재의 인식률 저하를 개선하기 위하여 BNN(Bayesian neural network)의 방식 중 하나인 MC(Monte Carlo) dropout을 활용한 화재 오인식 개선에 관해 연구하였다. BNN이 화재 인식 후 불확실성의 분포가 클 때 화재일 가능성이 작다고 판단하여 CNN의 화재 판단을 보류하는 방식으로 화재 인식률을 개선 시켰다. 총 100개의 학습되지 않은 이미지를 활용하여 CNN 방식과 BNN + CNN 방식 사용 시 추론 결과를 서로 비교하였다. 그 결과 약 13%가 불확실성이 높아 개선된 추론 결과를 얻었다. 전체 데이터 확인 결과 4% 정도 에러를 고려하면 CNN에 비해 약 9% 정도 개선된 결과를 얻었다.
Abstract
Accidents sometimes occur due to incorrect predictions of current deep learning models. Especially damage from fire or disaster is beyond our imagination. In this paper, we studied recognition rate improvement using Monte Carlo (MC) dropout, one of the Bayesian neural network(BNN) methods to improve the low recognition rate of fire when data collection is limited, such as a fire. When BNN recognized fire and the uncertainty distribution was large, it judged that the probability of a fire was low and improved the fire recognition rate by suspending CNN's fire judgment. One hundred untrained images were used to compare the inference results when using the CNN method and BNN + CNN method. As a result, approximately 13% had high uncertainty, resulting in improved inference results. As a result of checking the entire data, considering the error of about 4%, the results were improved by about 9% compared to CNN.
Keywords:
convolution neural network, bayesian neural network, MC dropout, deep learningⅠ. 서 론
Computer vision을 위한 AI(Artificial Intelligence) 학습 방법은 지난 몇 년 동안 매우 빠르게 발전했다. 최근 AI 딥러닝 모델들은 더 큰 모델을 확보하여 더 많은 데이터로 학습을 진행하고 있다. 하지만 모델이 커질수록 해석이 어려워지고 딥러닝 모델의 출력값을 얼마나 신뢰할 수 있을지 알기 어렵다. 또한 최근에 딥러닝 모델들이 잘못된 예측을 하는 경우가 발생하곤 했다. 예를 들면 테슬라 자율주행 사고와 우버의 자율주행 사고로 인한 첫 희생자가 좋은 예이다[1].
이 경우는 학습한 데이터에 잘못된 노이즈가 있거나 학습에 사용되지 않은 데이터가 입력으로 들어오는 경우다. 단순히 영상 데이터를 입력받으면 판단 결과를 확률로만 출력을 만들어 내는 함수와 같은 AI 딥러닝을 얼마나 신뢰하고 사용할 수 있을지 의문이 들 수 있다. 따라서 AI 딥러닝을 잘 모르는 것이 현재 사회의 중요한 문제가 되고 있다.
그래서 많은 연구자가 생각해 낸 방법이 딥러닝 모델의 불확실성, 즉 uncertainty를 정량화하는 것이다[2]. 이 경우 학습모델이 자주 보지 못한 패턴의 예측 데이터일수록 학습모델의 예측값에 대한 불확실성이 높게 나올 것이고, 이를 바탕으로 의사결정 단계에서 얼마나 AI 딥러닝 모델을 신뢰할 수 있을지를 결정할 수 있다.
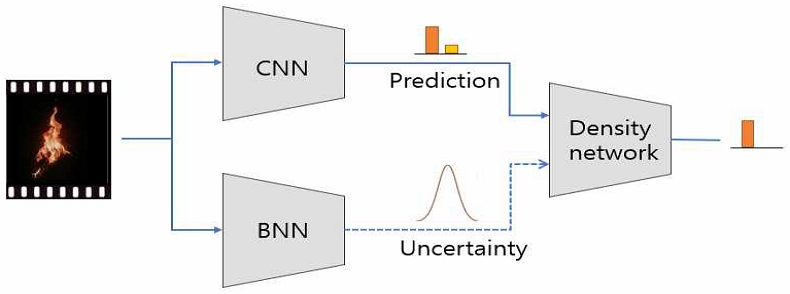
특히 화재나 재난과 같이 공개된 데이터가 제한되고, 모델의 신뢰도가 중요한 사항에서는 uncertainty를 고려한 의사결정이 더욱 중요한 문제가 되고 있다. 본 논문에서는 CNN(Convolution Neural Network)에서 추론한 화재 예측(확률)을 판단하기 전에 BNN(Bayesian neural network)을 이용하여 화재의 불확실성(분포)을 판단하고 예측값의 불확실성이 높으면 화재 판단을 보류하는 방식으로 화재 오인식 개선을 위한 새로운 방식을 제안한다. 그림 1은 BNN과 CNN의 기본적인 개념도를 그림으로 표시하였다.
Ⅱ. 관련 이론
2.1 Bayes rule
Bayes rule은 세 가지 종류의 확률로 정리가 된다. ① Posterior(P(wi|x)): 특징(x)가 주어졌을 때 그것이 특정 클래스에 속할 확률(사후확률), 즉 단서가 주어졌을 때, 최종적으로 구해야 하는 정답 값이다. ② Likelihood(P(xvertwi)): 특징(x)가 어느 정도 분포가 되어 있는지의 정보(가능도). 즉, 각 클래스에 어떤 형태로 분포돼 있는지 알려준다. Posterior를 구하는 데 매우 중요한 단서가 된다. ③ Prior(P(wi)): 특징과 관계없이 각 클래스의 비율이 얼마나 되는지의 값(사전확률). 보통 사전 정보로 제공되어 지나, 그렇지 않는다면 연구자의 경험을 통해 정해야 하는 값이다[3].
우리의 최종 목적은 Posterior(P(wi|x))을 구하는 것이며, 이것은 Likelihood(P(xvertwi))와 Prior(P(wi))를 이용하여 식 (1)과 같이 구할 수 있다.
| (1) |
그리고 A 대신 w, B 대신 x를 넣으면 식 (2)와 같이 된다.
| (2) |
좌변은 구하고자 하는 Posterior(P(wi|x))이고, 우변의 분자는 Likelihood(P(xvertwi))와 Prior(P(wi))이다[3][4]. 그리고 우변의 분모를 보통 Evidence라고 부르는데, 이 또한 Likelihood와 Prior를 통해 계산이 가능하다. 우리는 식 (2)를 이용하여 Posterior를 구할 수 있다. 즉 식 (2)가 Bayes’ Rule 또는 Bayesian Equation으로 부른다.
2.2 BNN(Bayesian neural network)
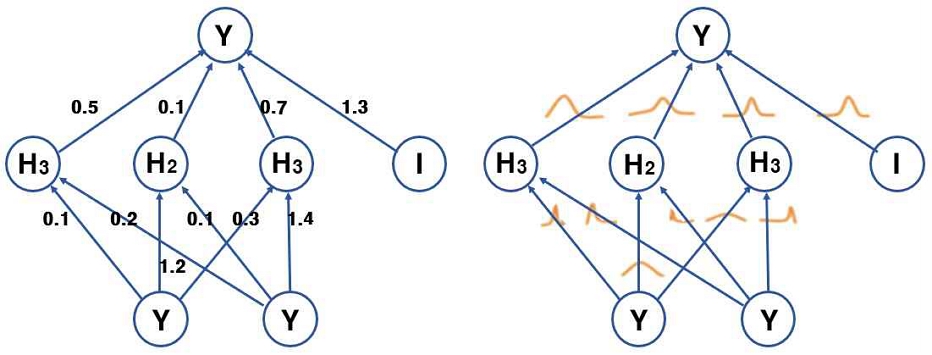
BNN과 CNN의 차이는 바로 Bayesian(분포)으로서의 접근법과 Frequentist(빈도)로서의 접근법이다. Bayesian은 관측된 데이터 저변에 깔린 prior distribution을 고려하여 예측한다면, Frequentist은 오로지 관측된 데이터만의 확률을 고려하여 어떠한 분포에 대해 예측하는 점이 다른 것이다. 즉 Frequentist들이 관심을 가지는 값은 Likelihood(P(xvertwi))이지만, Bayesian이 관심을 가지는 값은 prior distribution이 고려된 Posterior(P(wi|x)), 즉 posterior distribution이라고 볼 수 있다. 그림 2에서는 기존 CNN과 BNN의 동작 차이를 보인다.
기존의 딥러닝 모델들은 하나의 입력에 대해 하나의 출력 결과를 도출하는 방식이었다. 즉 point estimate 방식으로 우리가 사용하고 있는 Deep learning은 대부분 argmax(P(xvertwi))를 만족하는 하나의 weight point wi을 찾는 문제이다. 이 같은 방식을 MLE(Maximum Likelihood Estimation)이라고 한다. 반면 Bayesian은 P(wi|x), 즉 식 (2)를 구하는 방법을 말한다. 즉 posterior 그 자체를 구하는 것이다. BNN은 하나의 입력에 대해 여러 번의 출력을 얻고, 이 여러 출력의 분포를 구하는 것으로 볼 수 있다. 이 경우 출력의 분포에서 나오는 분산 값의 넓이를 uncertainty라 정의할 수 있다[5].
2.3 Monte Carlo dropout
Bayesian neural network의 여러 방법 중에서 가장 많이 사용되고, 가장 보편적으로 쓸 수 있는 것은 MC(Monte Carlo) dropout이다[6]. MC dropout에서는 필요에 따라 각 dropout layer를 활성화한 후 모델을 학습한다. 하지만 기존의 dropout과 달리, 추론 시에도 dropout을 활성화해, 여러 번의 출력값을 구한다. 이렇게 나온 출력값들의 분포를 Posterior probability에서 sampling 된 분포의 결과를 보고, 이 분포의 결과값을 통해서 Bayesian 모델링 관점에서의 uncertainty의 분포를 계산할 수 있다는 것이 MC dropout의 장점이다. 그렇다면 기본적인 모델링은 그림 3과 같이 마지막 FC(Fully Connected layer) 직전 activation layer 뒤에 MC dropout layer를 추가하는 방식이다[7]. 즉 그림 3에서 W2의 activation 뒤쪽에 위치한다.
그리고 MC dropout layer의 경우 다른 딥러닝 방식과 동일하게 optimization을 진행하면 된다. 그리고 Loss의 경우 다음과 같이 정의된다.
| (3) |
여기서 λ∥σ∥2는 L2 regularization에서 계산된 것이 아니고 Bayesian deep learning에서의 optimization 유도 과정에서 출력되는 부분이므로 생략하면 안 된다. Deep learning에서 Weight decay, 그중에서 L2 Regularization을 사용한다는 것은 주어진 data를 적용함과 동시에 w에 Gaussian distribution이라는 Prior를 걸어주어 MAP(Maximum A Posterior)를 통해 w를 구하겠다는 것이다. L2 Regularization을 적용하는 것은 w에 Gaussian distribution을 Prior로 걸어 주는 것이다.
2.4 GNN(Gaussian Neural Network)
GNN은 예측의 불확실성을 모델링하기 위해 Gaussian 분포를 사용하는 인공 신경망의 한 종류이며, 주로 확률적 머신 러닝 및 BNN에 많이 사용된다. Gaussian 신경망은 포인트 추정값뿐만 아니라 네트워크의 예측에 대한 확률 분포를 나타내는 데 사용된다. Gaussian 신경망의 주요 개념 및 구성 요소는 다음과 같다:
- Gaussian 출력층: 신경망 구조는 일반적으로 결정론적 출력층을 가지고 있다(예: 회귀의 경우 단일 스칼라값 또는 분류의 경우 소프트맥스 출력). 그러나 GNN은 출력층으로 Gaussian 분포를 사용한다. 이것은 단일 값을 예측하는 대신 가능한 값들에 대한 확률 분포를 예측한다는 것을 의미한다.
- 불확실성 모델링: GNN은 예측에 대한 불확실성을 찾기 위해 설계되었다. 로봇 공학, 자율 주행 차량 및 의료 진단과 같은 다양한 응용 분야에서 불확실성을 이해하는 것이 안전하고 신뢰성 있는 의사 결정에 중요하게 사용된다.
- 매개변수화: GNN에서 출력 레이어의 매개변수는 일반적으로 Gaussian 분포의 평균(μ)과 분산(σ2)이다. 이러한 매개변수는 데이터로부터 훈련 중에 학습된다. 이는 전통적인 신경망의 가중치와 편향과 유사하게 훈련된다.
- 훈련: GNN의 훈련은 일반적으로 예측된 Gaussian 분포 매개변수(μ와 σ2)를 사용하여 관측 데이터의 가능성을 최대화하는 것을 포함한다. 이것은 MLE(최대 우도 추정)와 유사하지만, Gaussian 분포를 Likelihood(가능도 함수)로 사용한다.
- 추론: 추론 중에 GNN은 점 추정뿐만 아니라 불확실성 추정도 제공한다. 예를 들어 회귀 작업의 경우 단순한 값 하나를 예측하는 대신 Gaussian의 평균과 분산을 제공하여 예측과 관련된 불확실성 수준을 표시할 수 있다[8].
- Bayesian 해석: GNN은 뉴럴 네트워크 내에서 Bayesian 추론을 수행하는 방법으로 볼 수도 있다. 이는 네트워크 내에서 불확실성의 전파를 가능하게 하며 모델 불확실성이 중요한 요소인 작업에서 유용하다.
Ⅲ. 제안하는 방법
3.1 BNN + CNN 방식
최근 AI 딥러닝 모델들은 더 큰 모델을 확보하여 더 많은 데이터로 학습을 진행하고 있다. 화재나 재난의 경우도 예외는 아니다. 하지만 모델이 커질수록 해석이 어려워지고 딥러닝 모델의 출력값을 얼마나 신뢰할 수 있을지 알기 어렵다. 또한 화재와 같이 한번 잘못된 예측을 하게 되면 치명적 사고로 이어질 가능성이 높아 매우 각별한 주의가 필요하다.
최근에 딥러닝 모델들이 잘못된 예측을 하는 경우가 자주 발생하곤 했다. 그래서 화재의 인식률 개선을 위해서 많은 데이터 확보도 중요하지만, 그에 못지않게 현재의 데이터만으로도 인식률 개선이 시급한 것도 사실이다.
그림 4와 같이 화재 오인식률을 개선하고 안정된 추론값을 얻기 위해 CNN + BNN 방식을 제안한다. 즉 제한된 데이터로 인한 CNN의 인식률 저하를 BNN을 활용하여 한 번 더 불확실성의 분포로 예측하여 준다면 적은 데이터에서 오는 화재 오인식 부분은 상당이 개선될 것이다. 한 장의 영상 이미지에서 여러 가지 객체 분류(Classification)가 검출될 경우 CNN에서 추론한 예측값과 BNN에서 추론한 불확실성의 분포를 계산하여 일정 범위 이상을 넘으면 분류 판단을 보류하는 방식이다.
좀 더 상세하게 설명하면 화재 영상 입력에 대해서 10번 샘플링을 통해서 여러 추론 값을 생성하고, 그 평균과 표준 편차를 구해서 최종 신뢰 구간을 계산한다. 그 후 CNN 추론 결과값과 BNN의 불확실성 분포를 활용하여 최종 화재 유무를 판단한다. 예를 들어 기존 CNN에서 화재로 판단한 부분이 BNN에서 불확실성이 80% 이상 높을 경우 none fire로 최종 추론 결론을 바꿈으로써 좀 더 안정적인 시스템을 구축할 수 있다.
이처럼 불확실성이 높은 경우 화재 판단을 보류하므로 화재 오인식에 대한 리스크를 줄이고 화재 유무 판단에 대한 정확도를 개선할 수 있다. 하지만 매번 CNN + BNN을 비교 추론하는 것은 실시간 속도 면에서 매우 불리하다. 그래서 본 연구에서는 실시간 처리 속도를 개선하기 위하여 CNN의 인식 정확도가 70% 이하일 경우에만 BNN의 불확실성 분포의 결과를 확인하는 방식으로 변경하였다.
3.2 병렬형 Monte Carlo dropout
BNN의 가장 큰 단점은 Posterior를 계산할 수 없는 데 있다. 그래서 이 문제를 해결하기 위하여 대표적으로 Variational inference 방법과 Monte Carlo Dropout을 사용하는 방법이 있다[9]. Variational inference는 Posterior인 P(wi|x)를 근사화하는 방식이다. 하지만 Monte Carlo Dropout은 Neural network에서 forward 학습 시, 임시로 네트워크를 랜덤하게 끊어서 딥러닝의 정규화 효과를 주기 위한 방법이다. 기존에는 추론 시 dropout을 사용하지 않는 방법으로 정규화를 이루었다면, MC dropout에서는 추론 시에도 dropout을 그대로 사용하여 여러 번의 추론 값을 만들어 내고 이 추론 값들을 이용하여 평균을 구하면 Posterior인 P(wi|x)를 P(wi|x) ≈ P(wi)와 같은 방법으로 근사화를 유도하였다[10].
본 논문에서는 MC dropout을 활용하여 불확실성을 측정하는 방법을 적용하였다. MC dropout은 결정론적인 가중치를 가지지 않고, 가중치의 정규 분포로부터 가중치를 추론하는 방법을 사용했다. 이렇게 되면 추론 과정에서 MC dropout sample 숫자만큼 추론 과정을 반복해야 한다는 단점이 있다.
그래서 본 연구에서는 처리 속도를 개선하기 위하여 MC dropout을 병렬 처리하여 CNN과 BNN을 분리하여 추론을 진행하였다.
Ⅳ. 실험 방법 및 결과
Bayesian neural network를 활용한 화재 오인식 개선 연구 실험은 CPU: AMD Ryzen 7 3700X 8-Core Processor 3.6 GHz, GPU: NVIDIA GeForce RTX 8000, RAM 32GB 컴퓨터 환경에서 실험하였다[11]. 초기 테스트 데이터 세트는 표 1에 표시된 것과 같이 5,565개의 수량으로 하였다. 5,565개의 적은 수량으로 학습 데이터를 활용한 이유는 불확실성을 높여 좀 더 많은 수의 불확실성 데이터를 확보하고 BNN이 얼마나 개선되는지를 보기 위해서다. 그리고 초기 학습 시 loss, mIOU, mAP는 표 1과 같다.
표 2에는 초기 labeled dataset 정보를 표시하였다. classification은 Fire, Person, Smoke, Spark 4개로 구분하여 진행했다. 수량은 label이 완료된 이미지를 의미한다. 이미지에 따라 중복 label이 상당이 포함되어 있다. 다만 화재와 연관이 없는 사람은 추론 결과에서 제외하였다.
4.1 실험 결과
초기 labeled data를 활용하여 CNN(Darknet-53)으로 학습을 진행하였으며, 화재 오인식을 확인하기 위한 객체 검출용으로 Yolov4를 활용하였다.
그리고 화재 오인식 유무를 확인하기 위하여 기존 CNN의 추론 결과와 BNN + CNN 추론 결과를 동일한 IOU에서 비교하여 인식률 차이를 기록하였다. BNN의 특징은 같은 한 장의 이미지에서도 판정 결과가 다른 확률 분포를 가지는 게 특징이다.
가중치(weight) 값이 확률로 존재하는 CNN과는 달리 BNN은 분포로써 존재하므로 같은 이미지/영상이라 할지라도 매번 결과가 다르게 나온다. 이 분포의 넓이가 불확실성의 크기를 표현하는데 학습 데이터가 부족한 부분에서 불확실성이 커지는 것을 알 수 있다. 이 불확실성이 큰 부분에 대해서는 화재 인식을 보류하거나 화재가 아닌 것으로 판단하여 오인식을 개선하는 방향으로 진행하였다.
실험을 위해 1차로 12개 이미지를 사용하여 측정하였으며, 표 3에는 CNN과 BNN + CNN의 불확실성이 클 경우 인식률 차이에 대해 실험한 결과를 표시하였다. 즉 실험 결과에서 알 수 있듯이 BNN의 불확실성이 클 경우 CNN의 평균 정확도가 매우 낮다는 것을 알 수 있다.
그림 5에는 전체 12개 이미지 중 추론 이미지와 차이가 있는 4개 이미지만 모아 상세히 설명하였다. Image 1의 경우에는 CNN에서는 연기를 2개 표시하였으나 BNN에서는 불의 경계면에 있는 연기는 불확실성을 0.95로 매우 높게 판단하여 추론에서 제외하였다. Image 3의 경우에는 연기를 CNN에서 추론한 연기를 BNN에서는 인식하지 못하였다. 33% 확률로 연기를 인식하였지만, 불확실성이 85%로 나와 추론 설정값인 80%를 넘어 연기로 인식하지 못하였다.
Image 4의 경우에는 CNN과 추론 결과와 비교한 결과 우측 연기 부분이 불확실성이 81%로 불확실성의 경계를 넘어 BNN과의 추론에서 차이를 보인다. Image 8의 경우는 참 좋은 예인데 CNN에서 불을 연기로 잘못 인식한 부분을 BNN에서는 확률 100%로 잘못된 추론으로 판단하였다.
불확실성이 높은 이미지 4장을 분석한 결과 현재 불확실성의 판단 기준인 80%는 불확실성의 경계면을 잘 표현하는 것으로 판단되나, 불확실성을 판단하기 위한 회수에 대해서는 현재의 설정인 10번에 대해 적당한지는 향후 충분한 검토와 최종 기준 정립이 필요해 보인다. 그림 6에는 1차로 테스트한 12개 이미지 모두를 사용하여 BNN을 활용한 불확실성 추론 결과 이미지를 CNN과 비교하여 표시하였다.
표 4에는 BNN의 불확실성을 토대로 하여 CNN의 정확도를 분석한 결과를 표시하였다. 학습이 되지 않은 무작위 100개의 이미지를 인터넷에서 다운받아 사용했다. 기존의 CNN 사용 시 추론 결과는 224개의 객체가 탐지되었으며, BNN + CNN 사용 시는 CNN과 동일한 추론 결과가 195개로 약 87%, 그리고 불확실성을 판단한 추론 결과는 29개로 약 13% 정도가 나왔다. 불확실성으로 판단된 29건(13%) 중에서 잘못된 추론을 한 false의 경우는 9건으로 나머지 20건에 대해서는 true로 추론을 한 결과를 얻었다. 이 의미는 20건에 대해서는 개선된 결과를 얻었으나 9건(약 4%)에 대해서는 여전히 개선이 되지 않았다는 것이다.
표 5에는 CNN과 BNN + CNN의 추론 시간을 분석한 결과를 표시하였다. 측정 결과는 100개의 이미지를 사용하여 추론한 결과이다. CNN의 인식 정확도가 70% 이하일 경우에만 BNN의 불확실성 분포의 결과를 확인하는 경우 CNN 대비 약 11초 정도 지연이 발생했다. 이것은 이미지 전부를 추론한 것보다는 4초 정도 개선된 결과다. 향후 실시간 추론을 위해서는 추가 연구가 요구된다.
Ⅴ. 결 론
본 논문에서는 화재 오인식을 개선하기 위하여 Monte Carlo Dropout 방식의 BNN을 사용하여 추론 값들의 평균을 구하는 방식으로 Posterior를 구하여 화재 불확실성을 개선하였다. 추론 단계에서 불확실성이 높을수록 화재 오인식이 높은 것으로 이번 실험을 통하여 확인할 수 있었다. 화재 불확실성이 높으면 화재 판단을 제외하는 방식으로 화재 오인식을 줄여 정확도를 개선하였다. 하지만 불확실성이 높다고 반드시 화재가 아니라는 보장도 없다. 실제 표 6에서와 같이 불확실성을 이용하여 추론 하더라도 약 4% 정도의 에러는 계속 존재했다. 하지만 BNN을 적용하지 않았을 때 비해 약 9% (13% - 4%) 정도의 불확실성이 개선되는 것을 확인할 수 있었다. 향후 추가 연구를 통하여 4%의 불확실성을 개선 및 BNN을 이용한 초기 데이터 라벨링 방식을 활용한 데이터 증강 연구가 필요해 보인다.
Acknowledgments
이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. RS-2023-00247045)
References
- A. Kendall and Y. Gal, "What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?", Proc. of the 31st International Conference on Neural Information Processing Systems, California, USA, pp. 5580-5590, Dec. 2017.
- C. M. Bishop and M. E. Tipping, "Bayesian Regression and Classification", IOS Press, Computer and Systems Sciences, Vol. 190, pp. 267-285, 2003.
- Hyeongmin Lee’s Website, "Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP)", Sep. 2018. https://hyeongminlee.github.io/post/bnn002_mle_map, [accessed: Oct. 10, 2023]
-
V. Mullachery, A. Khera, and A. Husain, "Bayesian Neural Networks", Machine Learning (cs.LG), arXiv:1801.07710, [cs.LG], pp. 25-32, Oct. 2018.
[https://doi.org/10.48550/arXiv.1801.07710]

- Y. Gal and Z. Ghahramani, "Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning", The 33rd International Conference on Machine Learning, New York, USA, Vol. 48, pp. 1050-1059, Jun. 2016.
-
K. Brach, B. Sick, and O. Dürr, "Single Shot MC Dropout Approximation", Machine Learning (cs.LG), arXiv:2007.03293, [cs.LG], Jul. 2020.
[https://doi.org/10.48550/arXiv.2007.03293]

- Yarin Gal, "What My Deep Model Doesn't Know", Jul. 2015. https://www.cs.ox.ac.uk/people/yarin.gal/website/blog_3d801aa532c1ce.html, [accessed: Oct. 10, 2023]
-
J. Choi, D. Chun, H. Kim, and H.-J. Lee, "Gaussian YOLOv3: An Accurate and Fast Object Detector Using Localization Uncertainty for Autonomous Driving", International Conference on Computer Vision (ICCV), Seoul, Korea, pp. 502-511, Oct. 2019.
[https://doi.org/10.1109/ICCV.2019.00059]

- B. Lakshminarayanan, A. Pritzel, and C. Blundell, "Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles", Proc. of the 31st International Conference on Neural Information Processing Systems, California, USA, pp. 6405-6416, Dec. 2017.
-
X. Li, S. Chen, X. Hu, and J. Yang, "Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift", Computer Vision and Pattern Recognition (CVPR), California, USA, pp. 2682-2690, Jun. 2019.
[https://doi.org/10.1109/CVPR.2019.00279]

-
J.-S. Kim and D.-S. Kang, "A Study on Fire Data Generation and Recognition Rate Improvement using F-guessed and Semi-supervised Learning", The Journal of Korean Institute of Information Technology, Vol 20, No. 12, pp. 123-134, Dec. 2022.
[https://doi.org/10.14801/jkiit.2022.20.12.123]


1991년 2월 : 부경대학교 전자공학과(공학사)
2020년 8월 : 동아대학교 전자공학과(공학석사)
2020년 9월 ~ 현재 : 동아대학교 전자공학과 박사과정
관심분야 : 영상처리, AI

1994년 5월 : Texas A&M 대학교 전자공학과(공학박사)
1995년 ~ 현재 : 동아대학교 전자공학과 교수
관심분야 : 영상처리, AI, 패턴인식