기동 표적 추적을 위한 도플러잔차 기반의 기동 탐지 기법

2.1 동역학 모델

3차원 직교좌표계에서의 스캔 k에서의 표적 상태 벡터를 다음과 같이 정의한다.

여기서 $$ x_k,y_k,z_k$$는 위치, $$ {\dot{x}}_k,{\dot{y}}_k,{\dot{z}}_k$$는 속도, $$ {\ddot{x}}_k,{\ddot{y}}_k,{\ddot{z}}_k$$는 가속도를 의미한다. 선형 시스템의 표적의 동역학은 다음과 같은 수식으로 표현할 수 있다[5][9].

여기서 F_k는 상태천이행렬(State transition matrix), w_k는 공정잡음(Process noise)으로 평균이 0이고 공분산으로 Q_k를 가지는 가우시안 백색잡음(w_k ~ N(0,Q_k))을 가정한다. 동역학 모델에 따라서 F_k와 Q_k가 달라진다. 본 논문에서 다루는 동역학 모델은 등속도(CV, Constant Velocity) 모델, Singer 모델, 정상 선회(CT, Coordinated Turn) 모델이며, 각 모델에 대한 정의는 다음과 같다[5][9]-[11].

CV모델은 백색잡음의 작은 가속도가 있는 거의 등속에 가까운 모델이다. 상태천이행렬과 공정잡음공분산은 다음과 같다[5][9][10].

Singer 모델은 표적의 가속도를 1차 마르코프 과정(Markov process)으로 가정한 모델이다. 상태천이행렬과 공정잡음공분산은 다음과 같다[5][9][10].

CT모델은 동일한 속력으로 동일한 선회율(Turning rate)로 회전하는 기동을 가정한다. 상태천이행렬은 다음과 같다[5][10][11].

여기서 ω는 선회율을 의미하며 다음과 같이 계산된다[5].

여기서 ∥•∥₂ 은 l²-norm을 의미한다. 공정잡음공분산은 다음과 같이 등가속도(Constant acceleration) 모델과 동일하게 설정할 수 있다[5][10][11].

2.2 Converted Measurement Kalman Filter

레이다는 신호처리를 통해 표적의 거리, u, v로 구성된 측정값을 얻는다. 따라서 측정값과 표적 상태변수 X_k와의 비선형 문제를 해결하여야 하며, 이를 위해 본 논문에서는 CMKF(Converted Measurement Kalman Filter)[12] 알고리즘을 적용하였다. 이 방식은 측정값을 직교좌표계의 변환측정값으로 변환 후, 선형 칼만 필터를 적용하는 방식으로 비선형 문제를 해결한다.

측정 모델은 다음과 같이 표현될 수 있다.

여기서 z_k는 측정값, v_k는 측정오차로 공분산 R을 가진다. h는 상태벡터와 측정값 사이의 관계를 표현하는 비선형 함수이다. 측정값을 직교좌표계로 변환한 변환측정값 z′_k에 대한 측정모델은 다음과 같이 표현할 수 있다.

여기서 v′_k 는 변환 측정잡음공분산(Converted measurement noise covariance)으로 공분산 R′_k을 가진다. R′_k는 편미분을 통해 다음과 같이 계산된다[10].

변환 측정값과 변환 측정잡음공분산을 활용하여 칼만 필터의 예측과 갱신단계는 다음 수식과 같이 표현할 수 있다[13].

여기서 K_k는 칼만 이득(Kalman Gain)이다.

2.3 IMM(Interacting Multiple Model)

IMM 알고리즘은 다중 필터 모델로부터 다중 가설을 결합하여 더 나은 추적성능을 얻을 수 있는 기법이다[5]. IMM 알고리즘은 혼합(Interacting), 예측(Prediction), 쇄신(Update), 결합(Combination)의 4가지 단계로 구성되며, 각 단계별 상세한 알고리즘은 [5]에 기술되어 있다. 본 논문에서는 CV, Singer, CT의 세 가지 동역학 모델을 활용한다.

3.1 기동 탐지

본 논문에서는 도플러잔차를 활용한 새로운 기동 탐지 기법인 DR(Doppler Residual based maneuver detector)을 제안한다.

DR은 빠르게 변화하는 도플러잔차를 활용하여 기동 탐지 지연을 줄이고 오탐지를 효과적으로 억제할 수 있다.

기동 탐지는 일반적으로 표적 기동에 대한 두 가설(표적이 기동하지 않는 중, 기동하는 중)에 대한 가설검정 문제로 정의된다[3]. 그러나 제안하는 기동 탐지 기법은 표적의 기동이 시작되고 추적필터가 이를 정확히 추적하지 못한 경우에 대한 대응을 위해 설계되었으며, 이에 맞게 다음과 같은 두 가설을 설정한다.

H₀ : 표적이 기동하지 않거나, 표적이 기동 중이며 추적필터가 표적의 움직임을 정확히 추적하는 중.H₁ : 표적이 기동 중이며 추적필터가 표적의 움직임을 정확히 추적하지 못하는 중.

제안하는 기동 탐지 기법은 초기 가설을 H₀으로 설정하고, H₀→H₁ 전환 조건, H₁→H₀ 전환 조건에 따라 매 스캔에 대한 가설을 결정한다. 가설 전환 조건은 뒤에서 기술한다.

표적의 속도가 변화하면 도플러속도는 즉각적으로 변화하므로 이를 활용하면 빠른 기동 탐지가 가능하다. 반면 속도 변화에 의한 영향이 시간적으로 누적되어 위치 변화로 나타나게 되므로 위치를 활용한 기동 탐지는 상대적으로 느릴 수 있다. 제안하는 알고리즘은 추적필터와 측정값 간의 도플러속도 차를 활용하여 기동을 빠르게 탐지한다. 더불어 마지막에는 추적필터와 측정값 간의 위치 차를 활용하여 오경보를 줄이고 더 정확하게 기동을 탐지한다.

추적필터의 예측 도플러속도는 다음과 같이 계산할 수 있다.

여기서 $$ {\overline{\mathbf{v}}}_{\mathrm{k}}$$는 예측상태벡터의 속도벡터를, $$ {\overline{\mathbf{u}}}_{\mathrm{k}}$$는 예측위치방향의 단위 벡터(Unit vector)를 의미하며, 각각 다음과 같이 정의된다.

여기서 $$ {\overline{\mathbf{X}}}_{\text{k}}$$는 예측상태벡터이다. 이때 도플러속도 측정값 z_d,k와 예측 도플러속도간의 차이(도플러잔차)는 다음과 같다.

현재 스캔 k와 이전 스캔 k-1의 도플러잔차의 변화는 다음과 같다.

ϵ_k는 평균이 0이고 분산이 S_d,k인 정규분포를 따른다(ϵ_k ~ N(0,S_d,k)).여기서 S_d,k는 잔차 공분산(Innovation covariance)으로 다음과 같다.

여기서 $$ {\sigma }_{d,k}^2$$은 도플러속도 측정 오차 분산을 의미하며, 정규분포의 합이므로 Δϵ_k ~ N(0,S_d,k-1+S_d,k)를 따르게 된다. 표적의 기동 변화가 발생하고 추적필터가 이를 따라가지 못하면, 시간에 따라 Δϵ_k 가 점점 증가하거나 감소하게 된다. 이러한 특성을 활용하여 연속된 N개의 스캔 i=k-N+1,k-N+2,...k에 대해서 모두 Δϵ_i ≥ θ_i를 만족하거나, 모두 Δϵ_i ≤ θ_i를 만족하는 경우 기동이 탐지된 것으로 볼 수 있다. 문턱치 θ_i는 다음과 같이 정의된다.

여기서 Φ^-1(x,μ,σ²)는 평균이 μ, 분산이 σ²인 정규누적분포의 역함수(Inverse normal cumulative distribution function)를 의미한다. 따라서 θ_i는 평균 0, 분산 S_d,i-1+S_d,i의 정규누적분포의 역함수를 확률 P_Δϵ에 대하여 계산한 것이다.

오경보를 줄이기 위해 위치 정보를 활용한 기동 탐지를 이어서 수행한다. 다음 수식과 같이 위치에 대한 마할라노비스 제곱 거리(SMD, Squared Mahalanobis Distance)를 계산할 수 있다.

여기서 z′_p,k는 위치에 대한 변환 측정값이며, S_p,k는 잔차 공분산으로 다음과 같이 계산된다.

여기서 R′_p,k는 위치에 대한 변환된 측정오차공분산이다. $$ {\delta }_{p,k}^2$$는 자유도(Degree of freedom) 3의 카이제곱분포(Chi-squared distribution)을 따른다고 가정한다. 따라서 카이제곱분포의 신뢰수준 1-α(예를 들면 90% 또는 95% 등)를 설정하고, 카이제곱분포 테이블을 활용하여 문턱치 λ를 구할 수 있다[14]. $$ {\delta }_{p,k}^2\ge \lambda $$ 인 경우 일정 수준의 신뢰구간을 벗어났으므로 기동에 의한 영향으로 본다. 여기서 도플러속도는 이전 스캔의 정보를 활용하는 반면 위치정보는 현재 스캔 k의 정보만 활용한다. 이는 기동이 시작된 직후에는 기동에 의한 위치 오차가 크지 않으므로, 이전 스캔의 위치 정보를 활용하여 기동 탐지를 수행할 경우 기동 탐지 지연 시간이 늘어날 수 있기 때문이다.

H₀→H₁ 전환 조건은 식 (31)과 같이 정의된다. 이는 최근 N 스캔에서 도플러잔차의 변화가 동일한 방향으로 확률범위 밖으로 벗어남과 동시에 위치 SMD가 확률범위 밖의 큰 값을 가질 때 전환된다. 반면 H₁→H₀ 조건은 식 (32)와 같다. 위치 SMD가 확률범위 내의 작은 값을 가진다는 것은 추적필터가 표적을 정확히 추적하게 되었음을 의미한다.

표적의 기동이 없는 경우에 H₀→H₁ 전환 오탐지 확률은 다음과 같은 방법으로 구할 수 있다. 각 스캔에 대한 도플러잔차의 변화는 서로 독립적이며, 모든 스캔 i에 대해 $$ P\left(\Delta {ϵ}_i\ge {\theta }_i\right)=P\left(\Delta {ϵ}_i\le -{\theta }_i\right)=P_{\Delta ϵ}$$을 가정하면, 오탐지확률은 다음과 같이 계산된다.

따라서 오탐지확률 P_fa와 신뢰수준 1-α을 설정하면 확률 P_Δϵ가 결정되고 이어서 식 (28)에 의해 문턱치 θ_i도 계산된다.

3.2 추적 기법

다중 모델을 활용하면 표적의 변화하는 동역학을 정확하게 추정할 수 있다[5]. IMM은 다중 모델을 활용하는 대표적인 방식이지만, 기동 변화에 대한 인식이 결정기반의 방식에 비해 느린 단점이 있다[2]. 따라서 기동 시작 후 추적 필터의 오차가 크게 발생하거나 심할 경우 추적을 소실할 수 있다. 이러한 한계를 극복하기 위해서 본 논문에서는 IMM에 결정기반 방식을 적용한 새로운 기법을 제안한다.

결정기반 방식에서 널리 사용되는 방식 중 하나는 잡음레벨 조정방식이다[2]. 이 방식은 표적의 기동을 공정잡음공분산이 증가하는 것으로 다룬다. 따라서 기동이 탐지되면 칼만 필터의 공정잡음공분산을 증가시켜서 기동하는 표적에 대해 정확한 추적이 가능하도록 한다[2]. 또한 공정잡음공분산이 커지게 되면 데이터 연관 게이트 크기가 증가하게 된다. 따라서 공정잡음오차를 증가 시키면서 표적이 게이트 내에 존재할 가능성을 높여 추적 소실을 방지할 수 있다. 공정잡음오차는 2.1장에 기술된 것과 같이 등속모델의 경우 q_CV, Singer모델의 경우 σ_m와 τ_m, CT모델의 경우 q_CT에 의해 결정된다.

본 논문에서 추적필터는 CV, Singer, CT의 3개 모델을 활용한 IMM으로 설정한다. 표적의 기동 탐지 여부 (H₀, H₁)에 따라서 표 1과 같은 파라미터로 공정잡음공분산을 설정한다. 표 1의 파라미터를 보면 H₀, H₁에 따라서 q_CV 값이 더 크게 적용된다. 이러한 방법으로 CV모델의 공정잡음을 크게 설정하면서 측정값을 더 신뢰하도록 하여 빠르게 표적을 추적할 수 있도록 한다. 또한 공정잡음공분산이 커지면 연관 게이트도 함께 커지므로 기동하는 표적을 연관할 가능성이 높아지게 된다.

Table 1.

Design of process noise error parameters

측정값과 트랙의 데이터 연관을 위해서는 간단하며 널리 사용되는 GNN(Global Nearest Neighbor)[10] 방법을 적용한다. GNN 연관을 위한 비용 함수(Cost function)는 위치와 도플러속도에 대한 SMD를 활용한다. 위치 SMD는 식 (29)와 같으며, 도플러속도 SMD는 다음 수식과 같이 계산된다.

최종 비용 함수는 H₁인 경우 $$ {\delta }_{p,k}^2$$로, H₀인 경우 $$ {\delta }_{p,k}^2+{\delta }_{d,k}^2$$로 설정한다. 표적 기동에 의해 추적필터 의 오차가 발생한 경우 도플러잔차는 급격히 커질 수 있으므로 이 경우 $$ {\delta }_{d,k}^2$$는 활용하지 않는다. 즉, 도플러를 활용한 연관을 사용하지 않는다. 이는 기동 시 도플러속도 SMD가 커져 연관이 되지 않아 추적소실로 이어지는 현상을 방지하기 위해 일시적으로 도플러속도 활용에 따른 이점(오연관 감소 등)을 포기하는 것이다. 그러나 곧바로 추적 필터가 표적의 기동을 정확히 추적하게 되면 제안하는 기동 탐지 기법에 의해 H₀로 전환되어 도플러속도를 연관에 다시 활용하게 된다. 이러한 적응적인 설정으로 인해 기동하는 표적을 추적하면서도 오연관이 증가하는 것을 제한할 수 있다.

4.1 시뮬레이션 설정

기동에 대한 성능을 확인하기 위해 다음과 같은 시나리오를 설정하였다. 자항공기(레이다)와 표적기는 서로 마주보고 다가오는 시나리오로 시작되며, 시작시점에서 표적기는 자항공기 기준 정북향 50km 거리에서 200m/s의 속도로 다가온다. 자항공기의 속도는 200m/s로 등속도 운동을 유지한다. 표적은 시나리오 시작 후 10초 동안 등속도 운동을 유지하며, 10초부터 동일한 가속도로 정상 선회 기동한다. 기동은 표적기 방향이 180° 변경되어 정북이 되면 종료한다. 시나리오는 총 30초 간 수행된다.

측정값 모의는 다음과 같은 방식으로 이루어진다. 레이다의 방위각과 고각 빔폭을 각각 3.4°로, 신호처리의 거리게이트를 ±500m로 가정하고, 추적 예측위치를 기준으로 표적이 빔폭과 거리게이트 범위 이내에 위치할 때 표적이 측정될 수 있다. 이때 표적 탐지확률은 0.9, 거리 측정 오차는 10m, 각도측정오차는 방위각 고각 각각 4mrad로 설정하였다. 또한 추적필터 예측값을 기준으로 거리 ±500m, 방위각 ±1.7°, 고각 ±1.7°, 도플러속도 ±200m/s 범위 내의 임의의 값을 가지는 측정값이 0.5의 확률로 탐지되도록 오탐지를 생성하였다.

제안하는 알고리즘(DR)의 비교대상알고리즘은 다음과 같다. 먼저 baseline은 제안하는 기동 탐지 기법과 기동 탐지 시 처리방법을 적용하지 않은 IMM 기반의 추적필터를 의미한다. 다음으로 MR(Measurement Residual based chi-square detector)[15]는 측정 잔차로부터 SMD를 구하고 카이제곱 테스트로 기동을 탐지하는 방식이다. 마지막으로 IE(Input Estimate based chi-square detector)[15]는 input estimation을 기반으로 카이제곱 테스트를 수행하는 방식이다. MR과 IE에 대해서는 기동 탐지만 해당 방법으로 수행하고, 나머지는 제안하는 알고리즘과 동일하게 처리한다.

4.2 추적유지율

표적의 기동의 크기와 추적주기에 따른 추적 유지 성능을 확인하기 위해 추적유지율(Track maintenance rate)을 지표로 활용한다. 추적유지율은 (추적시도 수-추적소실 수)/추적시도 수로 정의된다. 연관된 측정값이 없어 추적필터가 5회 이상 갱신되지 않으면 추적을 소실한 것으로 정의한다. 표적기동 가속도는 40, 50, ..., 90m/s²의 6개 설정, 추적주기는 0.2, 0.4, ..., 2.0[sec]의 10개 설정의 조합으로 총 60개의 설정에 대해서 결과를 확인하였다. 각 설정에 대해서 1000회의 Monte-Carlo 시뮬레이션을 수행하여 추적유지율을 계산하였다. P_fa = 0.05, α = 0.15로 설정하였다.

추적 유지율 결과는 그림 1과 같다. 좌측 상단에서부터 오른쪽 아래 순으로 각각 40, 50, 60, 70, 80, 90m/s² 가속도 시나리오에 대한 결과를 보여준다. 모든 가속도와 추적주기 설정에 대해서 DR의 추적유지율이 가장 높은 것을 알 수 있다. 가속도가 40m/s²일 때 제안하는 알고리즘과 다른 알고리즘 간의 추적유지율 차이보다 더 큰 가속도를 가질 때 차이가 큰 것을 알 수 있다.

Fig. 1.

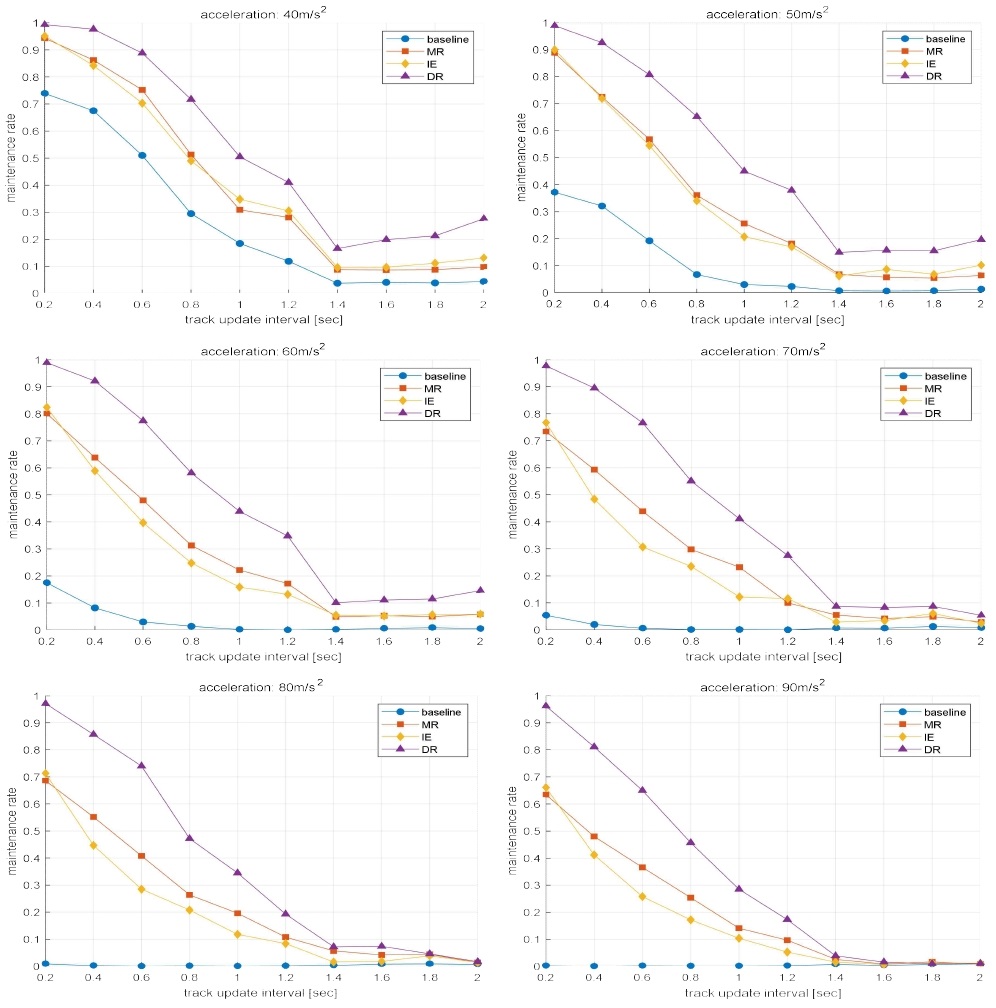
Track maintenance rates for different maneuver detection methods (acceleration: 40, 50, 60, 70, 80, 90m/s2)

이는 가속도가 증가함에 따라 발생하는 성능열화가 다른 기법들에 비해 제안한 기법에서 적게 나타나기 때문이다. 이 결과로부터 제안하는 알고리즘이 급격한 가속도 변화를 가지는 표적에 대해 강인한 것을 알 수 있다.

4.3 기동 탐지 지연시간

평균 기동 탐지 지연시간은 기동이 시작되고 기동을 탐지하기까지 걸린 평균적인 시간을 의미한다. 빠른 기동 탐지는 표적 기동에 대한 대응을 빠르게 할 수 있게 만들어 주므로 기동 표적의 추적성능에 큰 영향을 미친다. 4.2장의 추적 유지율과 동일한 설정으로 시뮬레이션을 수행하였다. 기동이 끝날 때 까지 기동 탐지에 실패한 경우는 평균 계산에서 제외하였다. 표 2는 각 알고리즘 별 평균 기동 탐지 지연시간을 보여준다. 각 가속도(Acc.), 추적주기(Interval) 설정 별 가장 짧은 지연시간을 보이는 값에 대해 볼드체로 강조하였다. 알고리즘 종류에 관계없이 가속도가 클수록, 추적주기가 짧을수록 지연 시간이 짧아지는 경향을 확인할 수 있다. 이는 가속도가 크면 가속에 의한 영향이 거리와 도플러속도에 잘 드러나므로 기동 탐지에 유리하며, 추적주기가 짧을 경우 자주 기동을 확인하여 빠르게 기동을 탐지할 수 있기 때문이다. 대부분의 경우 제안하는 알고리즘의 지연 시간이 가장 짧은 것을 확인할 수 있다. MR방식의 지연시간이 가장 길며, 다음으로 IE, 그 다음으로 DR이 가장 짧은 지연시간을 가지는 경향을 확인할 수 있다.

Table 2.

Average delay time of maneuver detection

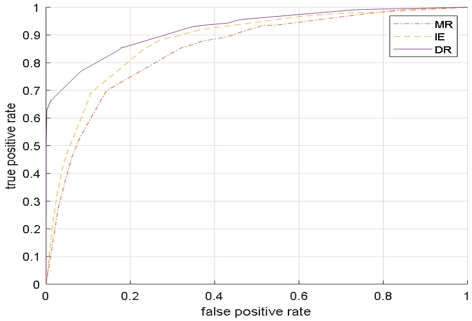
4.4 수신자 조작 특성 곡선

그림 2는 제안하는 기동 탐지 기법과 MR, IE의 수신자 조작 특성(ROC, Receiver Operating Characteristics) 곡선을 비교한 것이다. 이를 위해 시나리오 시작부터 기동이 끝나는 시간까지의 결과를 활용하였다. 기동 구간에서 H₁으로 판단한 이후 구간에 대해서는 참양성(True positive)로 간주한다. 가속도 60m/s²의 시나리오에서 추적주기는 0.5를 기준으로 P_fa를 변경하면서 각각 1000회의 Monte-Carlo 시뮬레이션을 수행하여 결과를 도출하였다. DR은 MR과 IE에 비해 더 좋은 성능을 보여준다. 특히 오경보율이 0.2이하인 구간에서 큰 성능 차이를 확인할 수 있다. 이를 통해 제안하는 알고리즘이 도플러속도와 위치정보를 연속적으로 활용하면서 오경보를 효과적으로 제거함과 동시에 좋은 탐지 성능을 얻을 수 있음을 확인할 수 있다.

Fig. 2.

ROC curves for different maneuver detection methods

5.1 시험 환경

비행시험 데이터는 항공기에 탑재된 AESA 레이다를 활용하여 획득하였으며, 표적기로는 FA-50(그림 4)을 활용하였다. 그림 3과 같이 레이다와 표적기는 각각 ‘s’로 표시된 지점에서 시작하여 ‘e’ 방향으로 이동하는 시나리오에서 시험을 수행하였다. 레이다는 직선기동을 하였고, 표적기는 레이다 방향으로 다가오다가 선회하여 반대방향으로 이동하였다.

Fig. 3.

Flight test scenario

Fig. 4.

Target aircraft (FA-50)

5.2 시험 결과

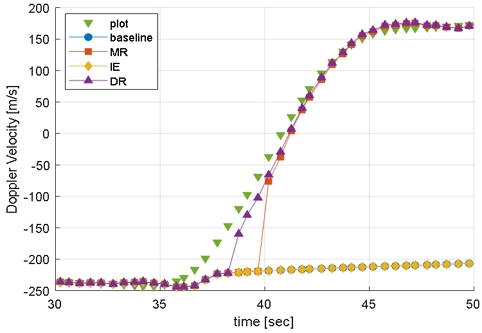
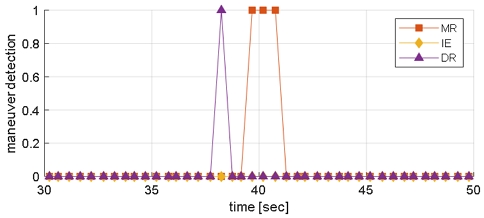
비행시험 중 탐지된 측정값을 활용하여 baseline, IE, MR, 제안하는 알고리즘에 대해 각각 추적을 수행하여 결과를 확인하였다. 시험을 위한 파라미터 설정은 4.2장의 내용과 동일하다. 표적은 약 35초부터 기동을 시작하였다. 그림 5는 도플러속도 측정값(Plot)과 각 알고리즘의 추적 예측 도플러속도값을 보여준다. baseline과 IE는 추적이 발산하여 표적의 도플러속도 변화를 쫓아가지 못하고 추적을 소실하였고, MR과 DR은 표적을 소실하지 않고 추적을 유지하였다. 그림 6은 동일한 시험에 대해서 기동 탐지 결과를 보여준다. IE는 기동을 탐지하는데 실패하였고, MR은 기동을 탐지하였으나, DR보다 늦게 기동을 탐지하였다. 제안하는 알고리즘은 표적 기동이 탐지되었을 때 연관게이트 크기를 늘리고 도플러속도를 연관에 사용하지 않는데, 이는 오연관을 증가시킬 수 있으므로 기동 탐지 횟수를 최소화하는 것이 좋다.

Fig. 5.

Tracking results for different algorithms using flight test data

Fig. 6.

Maneuver detection results for different maneuver detection methods

이러한 측면에서, MR 방식은 기동을 3회 연속 탐지하였고, DR은 1회만 탐지하면서 효율적으로 표적을 추적할 수 있음을 확인하였다.