최대가능도 기반 저경사 FMICW 레이다 다중표적 탐지 알고리즘

Ⅰ. 서 론

기존의 소형레이다의 경우 구현이 간단한 주파수 변조 연속파형(FMCW, Frequency Modulated Continuous Waveform) 방식이 널리 사용됐다[1][2]. 하지만 FMCW 방식은 송수신기가 동시에 작동하므로 Tx-Rx 안테나를 충분히 떼어놓을 공간이 부족한 경우 연결(Coupling) 문제가 발생하여 송신 힘을 높이기에는 한계가 있고 중거리 이상에는 사용할 수 없다.

이를 해결하고자 주파수 변조 간헐적 연속파형(FMICW, Frequency Modulated Interupted Continuous Waveform) 이 고안되었는데, FMCW와 달리 중앙 선스펙트럼(Center line spectrum) 외에 많은 거짓 선스펙트럼(Spurious line spectra)이 나타나서 표적의 거리와 속도 $$ r, \dot{r}$$을 알아내기 어렵고, 특히 다중표적의 경우 여분의 선스펙트럼의 개수가 기하급수적으로 늘어난다.

단일표적의 경우 가장 큰 파워를 갖는 중앙 선스펙트럼을 선택하는 것이 어렵지 않지만, 다중표적의 경우 수신 신호 양자화(Sampling)의 비격자(Off-grid) 현상에 의하여 표적 A, B가 같은 신호 대 잡음 비(SNR, Signal to Noise Ratio) 을 갖더라도 표적 B의 거짓 선스펙트럼이 표적 A의 중앙 선스펙트럼보다 파워가 높을 수 있어서 표적 A, B의 중앙 선스펙트럼을 선택하는 데 어려움이 있다.

표적의 도플러 주파수를 얻고자 할 때 표적과 레이다 간 상대속도가 크면 펄스 트레인을 사용하는 fast-ramp FMCW (혹은 FMICW) 방식보다는 몇개의 삼각파를 사용하는 저경사 FMCW 방식[3][4]이 적합하다. 하지만 저경사 FMCW(혹은 FMICW) 방식은 유령표적(Ghost target)을 제거하고자 다른 선형 주파수 변조 주파수들(Chirp or slopes)를 갖는 세 개 이상의 스위프(Sweeps) 를 사용하여, 세 개 이상의 식을 세워서 두 개의 미지수 $$ r, \dot{r}$$를 구하는데[3] 이와같이 과다 결정(Overdetermined) 방정식을 정확히 만족하는 해가 존재하지 않을 수 있고, 또한 몇 개의 스위프에서 다른 표적의 선스펙트럼이 중첩되어서 식을 세우는데 어려움이 있을 수 있다.

본 논문에서는 저경사 FMICW 레이다의 경우 최대가능도 기반[5] 순차적 표적 제거 방법을 사용하여 위에 나열한 문제들을 해결하였다. 또한 계산량을 줄이기 위하여 표적의 거리에 따라 미리 계산한 수신 신호를 저장한 사전(Dictionary)를 만들어 이용한다.

제 2장에서는 제안하는 기본 알고리즘을 설명하고, 제 3장에서는 10개의 표적이 있는 경우의 결과를 보이고, 결론은 제 4장에서 제시한다.

Ⅱ. 기본 알고리즘

2.1 FMICW 파형

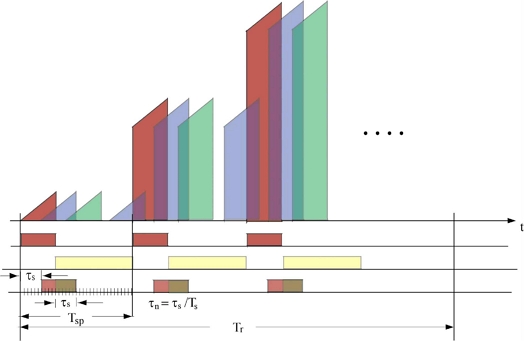
그림 1에 FMICW 파형의 일부분을 보였다. x 축, y 축은 각각 시간, 주파수를 의미한다. 또한, 붉은색과 노란색으로 표시된 직사각형 구간은 각각 송신기가 ON, 수신기가 ON인 구간을 의미한다. 붉은색 사다리꼴 파형은 송신 파형이고 파란색, 초록색 사다리꼴 파형은 표적의 거리에 따른 수신 파형이다[6].

Fig. 1.

Part of the FMICW waveform

여기서 초록색 수신 파형은 잘리는 부분 없이 온전하게 수신됨을 알 수 있는데, 스위칭(Switching) 주기 T_sp를 변화시켜서, 표적들의 거리가 크게 다르지 않다면 모두 온전하게 수신되도록 할 수 있다. 본 논문에서는 이의 경우만 고려한다.

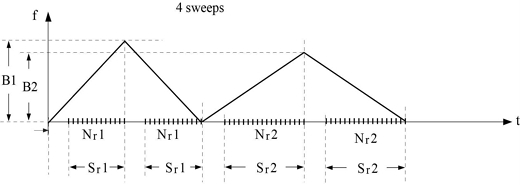
FMCW에서 range-Doppler 연결(Coupling)이 있으므로 잘 알려진 대로[3] 상/하(up/down) 두 개의 스위프 파형을 이용하여 단일표적의 $$ r, \dot{r}$$을 구하고, 또한 다중표적의 경우는 그림 2에 보인 바와 같이 두 쌍 (pair)의 상/하 스위프를 가지고 $$ r, \dot{r}$$ 을 얻는다. 본 논문에서는 FMICW에서도 그림 2와 같은 두 쌍, 즉 총 4개의 스위프를 사용한다.

Fig. 2.

Four-sweep waveform to be considered

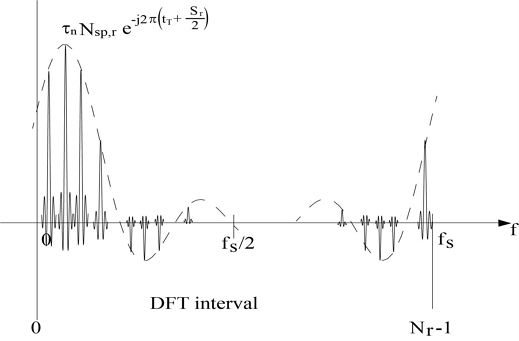
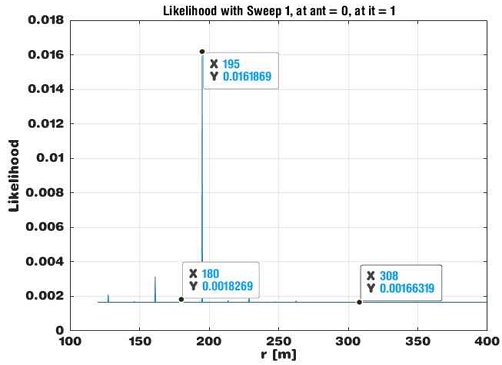
설명의 편의상 일단 표적이 정지하여 있다고 가정하고 네 개의 스위프 동안 수신한 양자화된 수열을 각각 y₁, y₂, y₃, y₄ 라고 하자. 이들을 각각 고속 푸리에 변환(FFT, Fast Fourier Transform) 하면 그림 3과 같은 선스팩트럼 z = dft(y_i)를 얻는다.

Fig. 3.

DFT of the received FMICW during one sweep

FMCW 파형의 경우 중앙 선스펙트럼 한 개만 존재하지만, FMICW는 그림 3에 보인 것과 같이 주변에 많은 거짓 선스펙트럼이 나타난다.

이들 선스팩트럼은 표적의 거리에 따라서 오른쪽으로 원형이동(Circular shift) 하므로 거리에 따라서 다른 형태를 보인다. 다중표적의 경우 중앙 선스펙트럼을 구별하는 것이 불가능하므로 본 논문에서는 이 패턴 전체를 가지고 표적의 거리를 구한다.

양자화된 여러 r 값에 대하여 네 개의 스위프에서 FFT 한 결과 a₁ (r), a₂ (r), a₃ (r), a₄ (r)를 미리 사전(Dictionary)으로 만들고 이들을 수신 신호의 FFT 값 z_i 와 비교하여, 가장 일치하는 r로부터 거리를 얻는다. 원래 파형 대신 FFT 결과로 사전을 만드는 이유는 이들 선스팩트럼은 N_r개 위치에서의 파워 복소수 값만으로 결정되므로 시간 파형과 비교하여 사전의 용량이 매우 적어지는 장점이 있기 때문이다.

2.2 제안하는 알고리즘

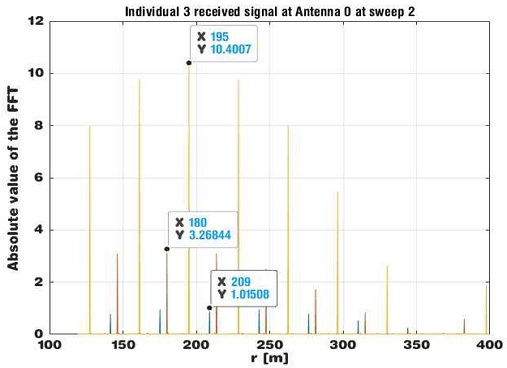
편의상 제안하는 알고리즘을 다음 표 1에 보인 것과 같은 3개의 표적으로부터 수신한 FMICW 신호를 가지고 설명하고자 한다.

Table 1.

Range and range velocity of three targets

그림 4에 스위프 2에서의 수신 신호 z₂를 보였다.

Fig. 4.

Received signal at sweep 2

네 개의 스위프에서 수신 신호를

$\[ \begin{array}{cc}{\mathit{z}}_i={\mathit{a}}_i\left(r\right)s_i+{\mathit{n}}_i,\hfill & i=\mathrm{1,2},\mathrm{3,4}\hfill \end{array} \]$

(1)

로 표시하면 표적의 거리 r_j에 대한 네 개의 최대가능도(MLE, Maximum Likelihood Estimation) 함수는 다음과 같다.

$\[ p\left({\mathit{z}}_{\mathit{i}}|r_j\right)\propto \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({\mathit{z}}_{\mathit{i}}-\mathit{a}\left(r_j\right)\right)}^H\left({\mathit{z}}_{\mathit{i}}-\mathit{a}\left(r_j\right)\right)/{\sigma }_n^2\right] \]$

여기서 1 ≤ i ≤ 4, 1 ≤ j ≤ 3이다. 이제 MLE $$ \widehat{\mathit{r}}=\left[{\widehat{r}}_1,{\widehat{r}}_2,{\widehat{r}}_3\right]$$는 이 함수를 최대로 하는 값으로서 다음과 같이 구할 수 있다.

$\[ {\widehat{r}}_j=\mathrm{a}\mathrm{r}\mathrm{g}\underset{r_j}{\text{min}} {∥{\mathit{z}}_{\mathit{i}}-{\mathit{a}}_{\mathit{i}}\left(r_j\right){\widehat{s}}_i∥}^2 \]$

(2)

여기서 $$ {\widehat{s}}_i={\mathit{a}}_i^H\left(r_j\right){\mathit{z}}_{\mathit{i}}/\left[{\mathit{a}}_i^H\left(r_j\right){\mathit{a}}_i\left(r_j\right)\right.⌉$$ 이다. 식 (2) 는 r의 비선형 함수 최적화 문제로서 계산량이 많이 필요하므로 미리 사전에 저장하여둔 a_i (r) 을 불러들여서 가장 정합(matching) 이 잘되는 $$ {\widehat{r}}_j$$, 1 ≤ j ≤ 3를 선택한다.

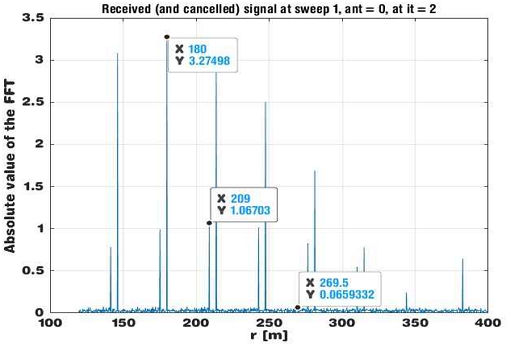
그림 5에 결과 $$ 1/{∥{\mathit{z}}_{\mathit{i}}-{\mathit{a}}_{\mathit{i}}\left(r_j\right)\widehat{s_i}∥}^2$$를 보였는데 그림 4와 비교하여 거짓 선스펙트럼은 많이 사라졌지만, 아직 표적 1의 거짓 선스펙트럼이 남아있고, SNR 0인 표적 3은 중앙 선스펙트럼조차 나타나지 않았음을 볼 수 있다. 그러므로 제안하는 방식은 단지 3개의 파워가 큰 선스펙트럼을 선택하는 것이 아니고 충분히 많은 큰 파워의 선 스펙트럼들을 4개의 스위프에 걸쳐서 선택하고 이들을 가지고 다음의 연관작업(Association)을 수행한다.

Fig. 5.

Matched filtering result at sweep 1

지금까지는 정지 표적을 가정하였지만 이동하는 표적의 경우 정합필터를 통해서 얻은 거리 r은 속도의 영향으로 실제 거릿값이 아니다. 이동표적의 $$ r, \dot{r}$$을 얻기 위하여 첫 번째 상/하 스위프 쌍에서 얻은 거릿값을 r₁ = r_u, r₂ = r_d로 정의하면, 실제 거리와 도플러는 잘 알려진 바와 같이[3]

$\[ \begin{array}{c}r=\left(r_u+r_d\right)/2,\hfill \\ \dot{r}=K_s\left(r_u-r_d\right)/\left(2f_c\right)\hfill \end{array} \]$

(3)

로 주어진다. 여기서 K_s = B/S, f_c는 대역폭의 중앙 주파수를 의미한다.

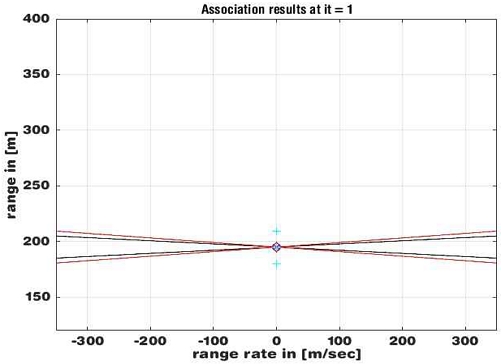
이 두 식을 그래프로 그리면 그림 6의 검은색 선이되고 교점이 $$ r, \dot{r}$$ 이다. 다시 두 번째 상/하 스위프 쌍으로부터 얻은 두 개의 식은 그림 6의 붉은 색으로 표시하였다. 두 검은색 선의 교점과 붉은색 선의 교점이 그림 6에 보인 것과 같이 일치하면 실제 표적이고 만약에 일치하지 않으면 유령표적이다.

Fig. 6.

Association result

하지만 위처럼 얻은 거친 추정값(Coarse estimates) $$ r, \dot{r}$$은 부정확하여 순차적 표적 제거에 사용할 수 없으므로 거친 추정값에서부터 다음에 설명할 정밀 탐색(Fine search)를 수행하여 정밀 추정값(Fine estimates)를 얻어야 한다.

이제 복소수 이득을 s, 4 스위프 동안 모은 측정값을 $$ \mathit{z}={⌈{\mathit{z}}_1^T,{\mathit{z}}_2^T,{\mathit{z}}_3^T,{\mathit{z}}_4^T⌉}^T$$, 측정 잡음을 $$ \mathit{n}\sim CN\left(0,{\sigma }_n^{2}I\right)$$ 이라 하면 신호 모델은

$\[ \begin{array}{c}\mathit{z}=\mathit{a}\left(r,\dot{r}\right)s+\mathit{n}\hfill \\ \mathit{a}\left(r,\dot{r}\right)={\left[{\mathit{a}}_1^T\left(r,\dot{r}\right),{\mathit{a}}_2^T\left(r,\dot{r}\right),{\mathit{a}}_3^T\left(r,\dot{r}\right),{\mathit{a}}_4^T\left(r,\dot{r}\right)\right]}^T\hfill \end{array} \]$

(4)

로 주어지며 최대가능도 함수는 다음과 같다.

$$ p\left(\mathit{z}|r,\dot{r}\right)\propto \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\mathit{z}-\mathit{a}(r,\dot{r})\right)}^H\left(\mathit{z}-\mathit{a}(r,\dot{r})\right)/{\sigma }_n^2\right]$$

그러므로 원하는 $$ \left(r,\dot{r}\right)$$은

$\[ \begin{array}{c}\mathrm{a}\mathrm{r}\mathrm{g}\underset{r,\dot{r}}{\text{min}} \parallel z-a\left(r,\dot{r}\right)\widehat{s}{\parallel }^2,\hfill \\ \widehat{s}={\mathit{a}}^H\left(r,\dot{r}\right)z/\left[{\mathit{a}}^H\left(r,\dot{r}\right)\mathit{a}\left(r,\dot{r}\right)\right]\hfill \end{array} \]$

(5)

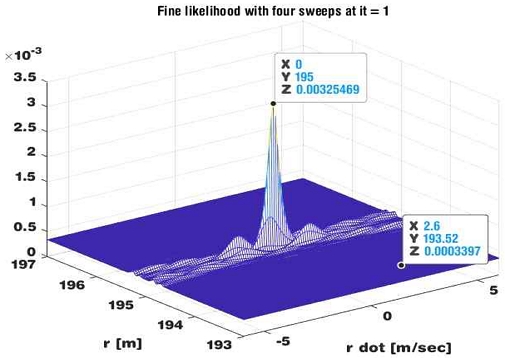
에서부터 구할 수 있다. 식 (5)의 최적화 문제는 정확성을 높이기 위하여, 양자화된 사전을 사용하지 않고 거친 추정값을 초깃값으로 하여 BFGS(Broyden-Fletcher-Goldfarb-Shanno) 알고리즘[7]으로 정밀 추정값 $$ \left(r,\dot{r}\right)$$을 얻는다. 그림 7에 결과를 보였다.

Fig. 7.

Result of the fine search

하지만 연관작업이 완벽하지 않으므로 이상과 같은 정밀 탐색결과가 유령표적이거나 거짓 선스팩트럼으로 인한 표적일 수 있으므로 정밀 추정값이 실제 표적인지 아닌지 확인하여야 한다.

제안하는 확인 방법은 과정은 정밀 추정값 $$ r, \dot{r}$$로부터 스위프 각각의 파형 $$ {\mathit{a}}_i\left(r,\dot{r}\right)$$, 1 ≤ i ≤ 4을 생성하고 수신 신호와 정합시켜서 $$ {\widehat{s}}_i$$를 찾고, 4개 스위프에 대하여 나머지 값(Residual), $$ {∥{\mathit{z}}_i-{\mathit{a}}_i\left(r,\dot{r}\right){\widehat{s}}_i∥}^2$$을 계산하여 최소한 한 개의 스위프에서 나머지 값이 잡음 레벨 이하이면 표적으로 판정한다. 서론에서 언급하였듯이 중첩되는 표적이 있을 수 있으므로 모든 스위프에서의 나머지 값이 잡음 레벨 이하 값을 가질 수는 없다.

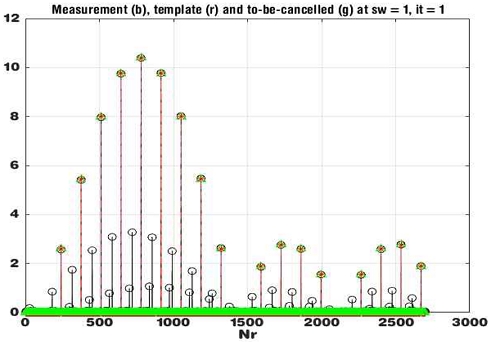
그림 8에 정밀 추정값 $$ r, \dot{r}$$로 만든 파형이 스위프 1의 수신 신호의 한 표적과 일치하므로 표적으로 판정한다.

Fig. 8.

Determination of true target

이제 생성한 파형을 수신 신호에서 빼면 그림 9와 같은 결과를 얻는다. 그림 4와 비교해 보았을 때 가장 높은 SNR 표적 1 이 정확히 제거되었음을 알 수 있다. 제거된 수신 신호에 다시 위의 과정을 적용하면 차례로 나머지 두 표적의 $$ r, \dot{r}$$을 얻을 수 있다[8].

Fig. 9.

Cancellation of the detected target

Ⅲ. 10개 무작위표적을 모의실험한 결과

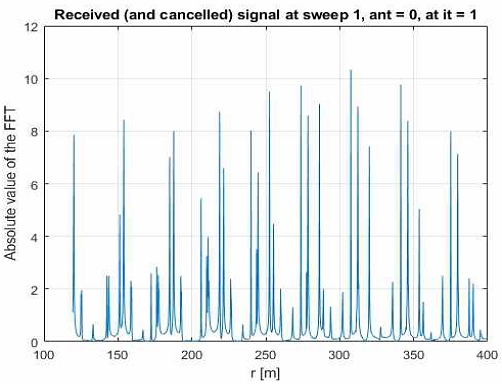
표 2에 무작위로 선택한 10개의 표적을 보였다. 이들 표적에 의한 스위프 1의 수신 신호는 그림 10과 같다. 다른 3개의 스위프도 비슷한 모양을 갖는데 표적들의 SNR이 크게 다르므로 10개 표적의 중앙 선스펙트럼을 수신 신호로부터 직접 알아내는 것은 불가능함을 알 수 있다.

Table 2.

Range and range velocity of ten targets

Fig. 10.

Received signal for 10 targets at sweep 2

제안한 알고리즘을 수행한 결과를 표 3에 보였다. 총 10번의 시행이 필요하였고, 첫 번째 회수에서 스위프 1, 2, 3, 4에 각각 14, 15, 13, 9개의 후보를 선택하였다.

Table 3.

Estimated range and range velocity of ten targets using the proposed algorithm

스위프 1, 2에서의 $$ r, \dot{r}$$의 범위를 만족하는 교점의 수는 34개, 스위프 3, 4에서는 25개가 나타났다. 이들 두 쌍의 교점의 거리가 작은 순으로 나열한 결과 4개의 후보 표적의 $$ r, \dot{r}$$을 얻었다. 이중 교점 간 거리가 가장 작은 표적(246.6231, 216.2084)를 선택하고 이 값을 시작점으로 하여 BFGS 알고리즘을 사용하여 정밀 추정값(246.2031, 218.1084)를 얻었다. 이 정밀 추정값으로 신호를 재현하여서 4개의 스위프의 측정치와 비교하였을 때 상쇄 오차가 스위프 1, 2, 3, 4 별로 0.45, 0.22, 1.29, 246.7로 나타난다. 가장 작은 상쇄 오차 0.45는 잡음 레벨 이하이므로 이 표적이 실제 표적이라고 판정하고 수신 측정값에서 빼고 두 번째 회수에 들어간다. 이를 반복하여 얻은 10개의 정밀 추정값은 표 2의 참값과 일치함을 알 수 있다. 또한, 대체로 높은 SNR 순으로 표적을 찾아 나감을 볼 수 있다.

Ⅳ. 결 론

고속 표적탐지에 적합한 저경사 FMICW 레이다를 위한 다중표적 탐지 알고리즘을 제안하였다. 제안한 알고리즘은 3단계로 이루어져 있는데, 다음과 같이 정리할 수 있다. 첫 단계에서는 1차원 최대가능도 최적화 문제를 사전을 사용하여 풀어서 표적들의 거리를 구한 후 연관작업을 통하여 거리와 속도를 대략 구한다. 두 번째 단계에서는 대략 구한 거리와 속도를 초깃값으로 하여 2차원 최대가능도 최적화 문제를 유사 뉴턴-랍슨 기법(Quasi Newton-Raphson iteration)으로 풀어서 정확한 거리와 속도를 구한다, 세 번째 단계에서는 정확하게 구한 거리와 속도를 이용하여 파형을 생성하고 수신 신호에서 뺀 후 나머지 표적들에 대하여 위의 작업을 반복한다. 제안한 알고리즘이 4개의 스위프를 사용하였을 경우 무작위로 생성한 10개의 표적에 대하여 거리와 속도를 정확히 찾아냄을 모의실험으로 보였다.

Acknowledgments

이 논문은 2019년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 연구임(UC190063FD)

References

• J. Hasch, E. Topak, R. Schnabel, T. Zwick, R. Weigel, and C. Waldschmidt, "Millimeter-Wave Technology for Automotive Radar Sensors in the 77 GHz Frequency Band", IEEE Transactions on Microwave Theory and Techniques, Vol. 60, No. 3, pp. 845-860, Mar. 2012. [https://doi.org/10.1109/TMTT.2011.2178427]
• F. Engels, P. Heidenreich, A. M. Zoubir, F. Jondral, and M. Wintermantel, "Advances in automotive radar: A framework on computationally efficient high-resolution frequency estimation", IEEE Signal Processing Magazine, Vol. 34, No. 2, pp. 36-46, Mar. 2017. [https://doi.org/10.1109/MSP.2016.2637700]
• C. Liu, S. Liu, C. Zhang, Y. Huang, and H. Wang, "Multipath Propagation Analysis and Ghost Target Removal for FMCW Automotive Radars", IET International Radar Conference, Chongqing, China, Nov. 2020. [https://doi.org/10.1049/icp.2021.0554]
• L. Rejfek, P. Bezousek, O. Fiser, and V. Brazda, "FMICW radar simulator at the frequency 35.4 GHz", 24th International Conference Radioelektronika, Bratislava, Slovakia, pp 1-4, Apr. 2014. [https://doi.org/10.1109/Radioelek.2014.6828452]
• H. V. Trees, K. Bell, Z. Tian, "Detection Estimation and Modulation Theory, Part I: Detection, Estimation, and Filtering Theory 2nd Edition", Wiley, May 2013.
• R. H. Khan and D. K. Mitchell, "Waveform analysis for high-frequency FMICW radar", IEE Proceedings-F, Vol. 138, No. 5, pp. 411-419, Oct. 1991. [https://doi.org/10.1049/ip-f-2.1991.0054]
• J. Stoer and R. Bulirsch, "Introduction to Numerical Analysis", Texts in Applied Mathematics, Springer, Vol. 12, 2002.
• T. Lee, J. Park, W. Yang, and J. Chun, "A Fast Sequential MLE Algorithm for Jet Engine Classification With Radar", in IEEE Sensors Journal, Vol. 20, No. 23, pp. 14157-14165, Dec. 2020. [https://doi.org/10.1109/JSEN.2020.3007857]
• S.-Y. Choi, B.-H. Lee, B.-J. Park, "Design of Multi Function Chip Correction Algorithm for Radar", The Journal of Korean Institute of Information Technology, Vol. 18, No. 6, pp. 81-88, Jun. 2020. [https://doi.org/10.14801/jkiit.2020.18.6.81]