그래프 합성곱 신경망과 임베딩 기법을 적용한 지식 그래프 엔티티 매칭 방법
초록
최근 소셜 미디어와 같은 빅데이터에 지식 그래프 임베딩 및 그래프 합성곱 신경망을 활용한 연구가 활발이 진행되고 있다. 그러나 현재까지 대규모 지식 그래프에 대한 엔티티 매칭 연구는 상대적으로 거의 연구가 되지 않고 있다. 대규모 지식 그래프는 아직 해결해야 될 이슈가 많지만, 그들 중 하나는 서로 다른 온톨로지를 사용하는 어휘 이질성 문제이다. 본 논문에서는 이 문제를 해결하기 위해 그래프 합성곱 신경망에 임베딩 기법을 함께 적용한 하이브리드 엔티티 매칭 방법을 제안한다. 우리는 실제 DBP15K 데이터셋을 사용하여 제안 방법을 기존 최신의 엔티티 매칭 방법들과 성능을 비교⋅분석하였다. 실험 결과 Hit@1에서 10.7%, Hit@10에서 5.9%, 그리고 Hit@50과 Hit@100에서 약간의 성능 향상을 보였다.
Abstract
Recently, studies using knowledge graph embedding and graph convolutional neural networks in Big Data such as social media are being actively conducted. Until now, however, entity matching studies on large-scale knowledge graphs have been relatively rarely studied. Although large-scale knowledge graphs still have many issues to be resolved, one of them is the vocabulary heterogeneous problem using different ontologies. To solve this problem, we propose a hybrid entity matching method that applies an embedding technique to a graph convolutional neural network. We evaluated the performance of the proposed method with existing state-of-the-art entity matching methods using a real DBP15K Dataset. The experimental results showed 10.7% on Hit@1, 5.9% on Hit@10, and slight performance improvements on Hit@50 and Hit@100.
Keywords:
entity matching, graph convolutional network, knowledge embedding, heterogeneity, knowledge graphsⅠ. 서 론
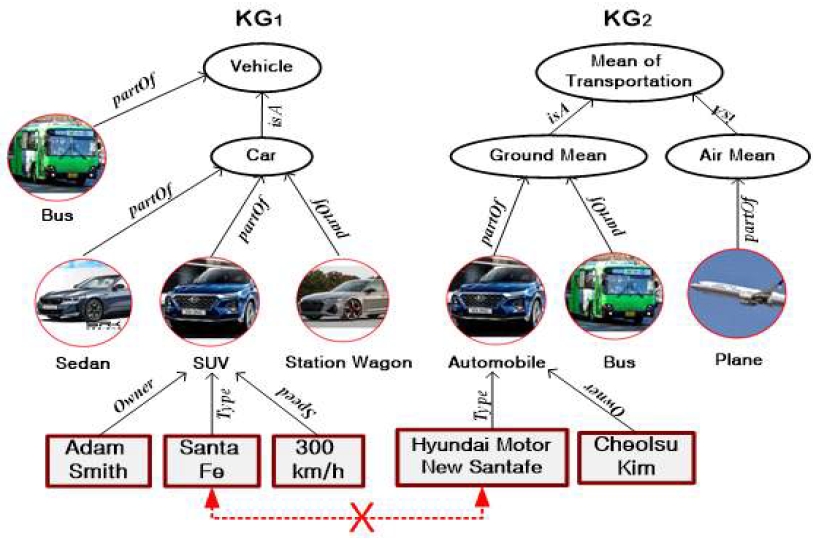
최근 신경망 분야의 비약적인 발전으로 WordNet, Freebase, Wikidata와 같은 대규모 지식 그래프에 딥러닝(Deep learning)이나 데이터 예측과 같은 연구가 활발히 수행되고 있다[1]. 그러나 현재까지 대규모 지식 그래프에 어떻게 정보가 임베딩(Embedding)되고, 어떻게 신경망 모델을 훈련시키고, 어떻게 엔티티 매칭이 수행되는지는 상대적으로 거의 연구가 미비한 상태이다. 이를 해결하기 위한 가장 어려운 이슈들 중 하나는 서로 다른 라벨링(Labelling)을 사용하는 어휘 이질성(Heterogeneity) 문제이다. 그림 1은 하나의 예를 통해 어휘 이질성 문제를 보여준다. 두 개의 지식 그래프(KG, Knowledge Graph) KG1과 KG2에서 원형은 엔티티 식별자를 사각형은 속성값을 나타내고 있으며, 여기서 Vehicle과 Mean of Transportation, Car와 Automobile 등은 동의어로 인식되지만 “Santa Fe”와 “Hyundai Motor New Santafe”는 같은 의미이지만 기존의 방법에서는 매칭이 되지 않는다. 이는 워드넷(WordNet) 등 동의어 집합만 엔티티 매칭에 사용되기 때문에 같은 동의어 집합에 속하지 않는 것은 매칭이 되지 않기 때문이다.
최근 링크 자동 완성(Automatic completion) 분야 등에 임베딩 기법들을 적용한 연구는 상당한 진전이 이루어졌지만, 이러한 기법들을 활용하여 지식 그래프 엔티티 매칭을 수행하기에는 아직 정확도가 많이 부족하다[2]. 따라서 본 연구에서는 어휘 이질성 문제점을 해결하기 위해 그래프 합성곱 신경망(GCN, Graph Convolutional Network)에 임베딩 기법을 함께 적용한 하나의 하이브리드(Hybrid) 엔티티 매칭 방법을 제안한다. 이는 복잡한 엣지 구조와 관계를 더욱 잘 표현하는 이중 그래프(Dual graph) 합성곱 신경망을 사용하고, 매칭의 정확도와 속도를 높이기 위해 지식 그래프 임베딩 기법을 사용하여 엔티티들을 비교한다. 제안 모델에서는 복잡한 GCN 모델을 바로 적용하기 전에 임베딩 기법을 사용하여 사전에 매칭되는 에티티들을 찾고, 다음 단계로 이중 그래프 합성곱 신경망으로부터 만들어지는 지식 그래프 엔티티의 거리를 정렬한 후, 이 중에서 거리가 가장 가까운 엔티티를 최종적으로 딥러닝이 찾은 매칭 값으로 선정한다.
제안 방법은 기존 최신의 엔티티 매칭 방법들보다 약 10%의 성능 향상을 보인다. 본 논문의 구성은 2장에서 관련 연구를 살펴보고, 3장에서 GCN과 임베딩 기법을 활용한 엔티티 매칭 기법을 제안한다. 4장에서 시스템 성능을 분석하고, 5장에서 결론을 내린다.
Ⅱ. 관련 연구
2.1 단어 임베딩
단어 임베딩(Word embedding)은 유사한 단어들이 인접한 거리에 위치하도록 각 단어에 해당하는 벡터값을 찾는 것이다. 예를 들면, 요리와 관련된 “soap” “chicken” “noodle,” 음악과 관련된 “saxophone” “violin” “piano,” 그리고 컴퓨터와 관련된“keyboard” “software” “monitor” 단어들이 클러스터링되어 가까운 위치의 벡터로 표현되도록 한다. 이를 이용하여 전문가 추천시스템이나 검색 엔진에 효과적으로 활용 가능한데, 대표적인 기법으로 Word2Vec[3], FastText[4], StarSpace[5] 등이 있다. 하지만 기존 임베딩 방식은 텍스트 말뭉치로부터 엔티티를 학습하여 벡터를 생성하기 때문에 말뭉치가 존재하지 않는 지식 베이스인 경우 올바른 엔티티 벡터값을 구할 수 없고 관계 그래프 모델 구축 시 성능 저하를 가져온다.
2.2 지식 그래프 임베딩
지금까지 수행된 임베딩 기반 엔티티 매칭 방법으로는 MTransE[6]와 IPTransE[7] 모델이 있다. MTransE 모델은 기존의 단일 언어 지식 그래프를 완성시키는 방법들과는 다르게 다국어 언어 지식 그래프 엔티티 매칭을 연구하였다. MTransE 모델은 분리된 임베딩 공간에서 각 언어의 엔티티와 관계를 인코딩함으로써 단일 언어 임베딩의 기능을 유지하면서 각 임베딩 벡터에 대한 전환을 다른 공간의 교차 언어 대응물로 제공하는 전략을 세웠다. 식 (1)은 MTransE 모델의 손실 함수를 나타낸다. 즉, 각 언어 L에 대한 k차원의 임베딩 공간이 벡터에 할당되고 TransE의 기본 구조를 채택하여 다양한 관계 컨텍스트에서 임베딩을 균일하게 표현한다.
| (1) |
여기서, h는 head, r은 relation, 그리고 t는 tail을 나타낸다.
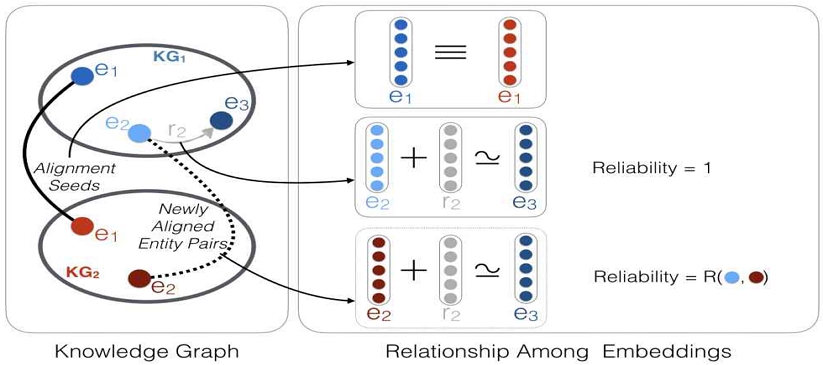
IPTransE 모델은 정렬된 엔티티의 작은 시드 세트에 따라 다양한 지식 그래프의 엔티티와 관계를 통합된 저차원의 의미 공간으로 인코딩하는 방식을 사용한다. 이 과정에서 공통 시맨틱 공간에서 시맨틱 거리에 따라 엔티티 매칭을 실행한다. 그림 2는 IPTransE 모델의 전체 구조를 보여준다. 파란색과 빨간색 점은 각각 지식 그래프 KG1과 KG2의 엔티티를 나타내며, 회색 화살표는 지식 그래프 간의 관계를 나타낸다. 실선과 점선은 반복적으로 엔티티와 대응물을 정렬하고 점점 더 신뢰도 높은 정렬 엔티티를 고려한 새로 정렬된 엔티티 쌍을 나타낸다.
지식 그래프 임베딩 방법은 특징(Feature)을 추출하는데 비교적 사람의 직접적인 개입이 덜 필요하고 대규모 지식 그래프로 확장이 가능하다는 장점은 있으나, head + relation ≈ tail이라는 가정에 의한 제약으로 복잡한 관계형 그래프에 존재하는 관계 정보들의 정확한 캡쳐링이 부족하다.
2.3 그래프 합성곱 신경망
GNN(Graph Neural Networks)은 그래프 구조의 데이터를 입력으로 사용하는 인공 신경망으로 그래프 노드 사이의 상관관계를 모델링하며 소셜 네트워크, 분자 구조, 3D Mesh 분야에 많이 활용되고 있는 기술이다. GCN은 GNN에 합성곱 연산을 사용하는 기법으로 엔티티 매칭에 활용될 수 있는데 그 중 하나가 GCN-Alignment[8]이다. GCN-Alignment는 GCN을 활용해 교차 언어 지식 그래프 정렬을 위한 새로운 접근 방법을 제시하였다. 하지만 GCN-Alignment는 기본적으로 무방향성을 가지며 레이블이 없는 그래프에서 작동하기 때문에 지식 그래프의 유용한 관계 정보를 무시하는 단점이 있다. R-GCN(Relational GCN)[9] 모델은 다중 관계 그래프를 모델링할 수는 있으나, 각 관계를 위한 각각의 가중치 행렬을 사용하여 너무 많은 매개변수들을 처리해야만 한다. DPGCNN(Dual-Primal Graph CNN)[10]은 노드(Node)를 기반으로 한 원 그래프와 에지(Edge)를 이용한 이중 그래프로부터 convolution 연산을 교대로 수행하고, 그래프 어텐션(Attention) 메커니즘을 연속적으로 적용하여 에지 관계를 향상시킨다. 이러한 DPGCNN의 아이디어로부터 관계 인식을 더 잘 표현하고 다중 지식 그래프들 간의 관계를 더 잘 인지할 수 있는 RDGCN(Relation-aware Dual-Graph Convolutional Network)[11]이 연구되었다. 기존 MtransE와 IPTransE 같은 임베딩 모델들의 단점을 보완한 RDGCN은 원 그래프와 이중 관계 그래프의 상호작용을 통한 메커니즘을 활용해 더욱 좋은 지식 그래프 표현 학습을 보여준다. 하지만 RDGCN은 비교적 좋은 성능에도 불구하고 실제 시스템에 적용하기에는 아직 매칭 정확도는 많이 부족하다.
Ⅲ. GCN과 임베딩을 활용한 엔티티 매칭 기법
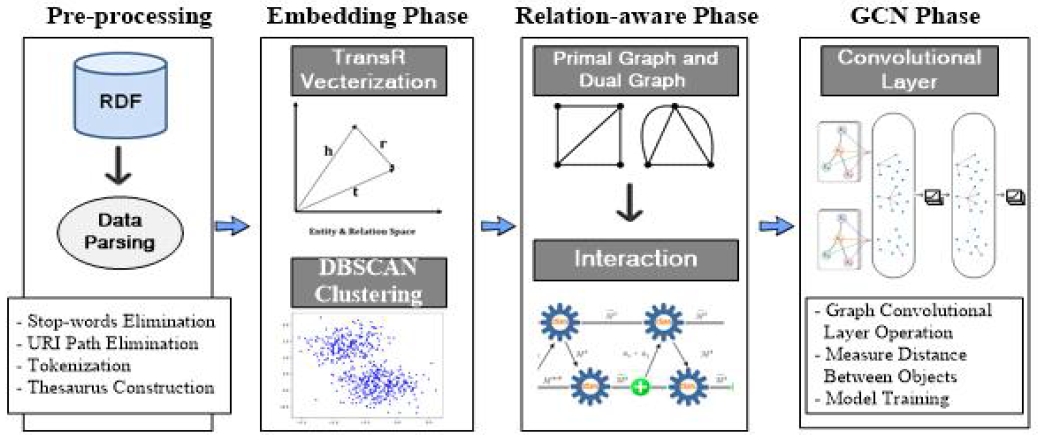
본 논문에서 제안한 지식 그래프 엔티티 매칭 기법은 그림 3과 같이 4단계, 즉, 전처리(Pre-processing) 단계, 임베딩 단계, 관계 인식(Relation aware) 단계, 그리고 그래프 합성곱 신경망(GCN) 단계로 구성된다.
3.1 전처리 단계
다양한 지식 그래프 데이터셋들을 활용하기 위해서는 정확한 엔티티 매칭이 필수적이다. 엔티티 매칭은 서로 다른 데이터셋의 속성값들 중 같은 의미를 가지는 값들을 찾는 것을 의미한다. 일반적으로 지식 그래프는 RDF(Resource Description Framework) 형식으로 구성되어 있으며 엔티티는 URI(Uniform Resource Identifier) 형태로 이루어져 있다(예, http://dbpedia.org/resource/2022_Asian_Games).
따라서 이러한 RDF 데이터를 그대로 활용하기는 어렵기 때문에 엔티티 매칭을 위해서는 엔티티 추출을 위한 데이터 파싱 작업을 해야 한다. 엔티티 형태는 자유롭게 작성되기 때문에 괄호, 콤마, 밑줄, 조사 등 다양한 불용어(Stop-word)들이 포함되어 있다. 추후 유사도 측정을 위해 불용어를 제거하고, URI 주소 경로 제거 및 토큰화 등을 통해 매칭에 문제가 없도록 파싱 작업을 수행한다.
3.2 임베딩 매칭 단계
이 단계의 주요 목적은 가장 성능 좋은 임베딩 방법을 사용하여 엔터티를 벡터로 변환시키는 것이다. 지식 그래프 임베딩 모델은 번역(Translation) 모델, 시맨틱 매칭(Semantic matching) 모델, 그리고 딥러닝(Deep learning) 모델로 분류할 수 있는데, 이들을 평가하여 최고의 성능을 보이는 방법을 대표 임베딩 모델로 선정한다. 본 논문에서는 번역 모델에서 TransE와 TransR, 시맨틱 매칭 모델에서 ComplEx와 DistMult, 그리고 딥러닝 모델에서 ConvE가 선택되었다. 실험 결과(본 논문 4.1 참조) 번역 모델의 성능이 다른 모델들보다 우수하다는 것을 보여주었다. 특히 TransR 모델이 가장 우수한 것으로 평가되었다.
제안된 임베딩 매칭 방법은 세 단계로 구성된다. 첫 번째 단계는 트리플 벡터를 얻기 위해 대규모 지식 그래프에 대한 임베딩 처리를 수행하는 것이다. 투영된(Projected) head와 tail 노드들은 식 (2)와 같이 프로젝트 행렬 M(r)에 의해 매핑되고[12], 점수 함수는 식 (3)과 같이 된다.
| (2) |
| (3) |
두 번째 단계는 DBSCAN(Density-based Spatial Clustering of Application with Noice) 알고리즘을 사용하여 벡터화된 트리플을 클러스터링하고 각 클러스터의 중심을 찾는다. DBSCAN은 밀도가 높은 영역을 기준으로 크러스터를 생성하고 밀도가 낮은 영역에 홀로 있는 점을 이상값으로 표시한다. DBSCAN은 반지름의 길이와 그 반지름이 갖는 원안에 들어가는 최소한의 개체수를 지정해 줘야 하는데, epsilon(ϵ)는 개별 데이터를 중심으로 ϵ 반경을 가지는 원형의 영역이고 minPts는 그룹을 묶는데 필요한 최소 개체수로 ϵ 주변 영역에 포함되는 타 데이터의 개수이다. 코어 포인터를 통해 주어진 반경 내의 모든 이웃을 그룹화하고 밀도에 따라 클러스터를 형성하기 때문에 기하학적인 모양을 갖는 군집도 찾아낼 수 있다. 클러스터의 중심은 식 (4)와 같이 각 차원을 따라 측정값을 평균화하여 찾은 n차원 데이터 공간에 있는 포인터로 정의된다.
| (4) |
여기서 Sc는 Nc 개체를 포함하는 클러스터 c의 인덱스 집합을 나타내며, 클러스터 중심 와 같다.
세 번째 단계로 중심점에 따라 두 KG로부터 크러스터 쌍들을 매칭시킨다. 만일 두 개의 엔티티 사이의 거리가 가장 가까우면 엔티티는 매칭된다. k-NN(k Nearest Neighbor) 알고리즘은 주어진 중심점에 가장 가까운 벡터를 찾는데, 이를 유사성(Similarity) 또는 근접(Approximation) 검색이라고도 한다. 이 알고리즘을 고차원 공간에 적용하면 NN 사이의 거리가 멀어질 수 있으므로 성능 저하 현상이 나타날 수 있다. 따라서 기존의 많은 연구에서는 정확한 NN의 근사치를 찾는 데 중점을 두고 있다. 근사 NN 알고리즘은 벡터 유사도(예: Cosine Similarity 및 Euclidean Distance)를 통해 주어진 중심점과 각 트리플 벡터 간의 유사도를 측정할 수 있다. 현재까지 여러 실험에서 Euclidean Distance가 뛰어난 정확도를 제공한다는 것이 입증되었으므로 우리는 이를 관련성의 척도로 채택하였다. 즉, 벡터화된 중심점 c와 트리플 v가 n차원 임베디드 공간에서 각각 좌표 (c1, c2, ...cn)과 (v1, v2, ...vn)을 갖는다고 하면 c와 v 사이의 거리 d(c, v)는 식 (5)와 같다.
| (5) |
다음으로 GCN 기반 모델의 일치 정확도를 개선하기 위해 데이터셋에서 발견된 엔터티들에 대해 마크가 표시되고 다음 단계에서 필터링된다. 마지막으로 필터링된 KG는 GCN 모델을 사용하여 학습된다.
3.3 관계 인식 단계
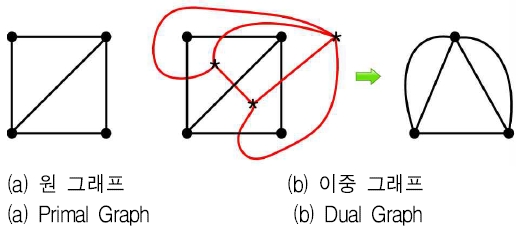
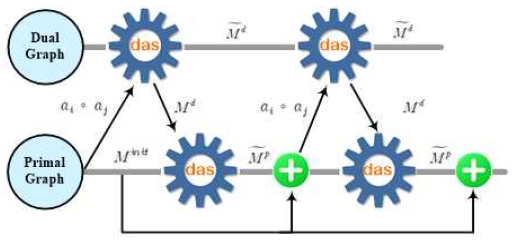
기존의 GCN 모델에서 관계 정보를 좀 더 잘 표현하기 위해 원 그래프(Primal graph)로부터 이중 그래프(Dual graph)를 도입하여 서로 상호작용 시킨 그래프로 GCN을 개선시킨 엔티티 매칭을 수행한다. 이중 그래프란 원 그래프에서 각 면마다 하나의 정점(Vertex)을 할당하고 인접한 두 면 사이에 하나의 에지를 연결시켜 만든 그래프를 말한다. 그림 4는 원 그래프와 이중 그래프의 한 예를 보여주고 있다.
이중 그래프의 두 정점 간에 유사한 head나 tail을 공유할 수 있는 가능성에 따라 식 (6)과 같은 가중치 w를 부여하고, 두 그래프 간의 상호 작용을 촉진시키기 위해 그래프 어텐션 메카니즘을 반복적으로 적용한다.
| (6) |
이중 그래프의 정점 vi에서의 출력 형태 는 식 (7)과 같으며, 여기서 은 이웃하는 인덱스의 집합을 나타내고, 는 이중 어텐션 점수(das, dual attention score)이고, 는 이중 그래프 정점 vj값이다.
| (7) |
여기서 정규화 시키기 전 이중 어텐션 점수(das)는 식 (8)과 같다. ai ∘ aj는 원 데이터에서 릴레이션 ri에 관련된 정점 매트릭스를 접합(Concatenation)하는 수식이고, FC은 입력을 스칼라로 매핑하는 완전 연결 계층(Fully connected layer)이며, wij는 가중치를 의미한다.
| (8) |
최종적으로 이를 정규화시키면 식 (9)와 같은 형식이 된다.
| (9) |
한편, 원 그래프 어텐션 점수도 이중 그래프 어텐션 점수와 비슷하게 계산될 수 있는데, 다만 여기서는 식 (10)과 같이 이중 그래프의 출력 형태인 를 사용하는 것이 차이점이다.
| (10) |
원 그래프의 정점 vi에서의 출력 형태 는 식 (11)과 같이 근거를 명확하게 보존하기 위해 초기 매트릭스를 더한다.
| (11) |
이렇게 이중 그래프와 원 그래프 사이에 여러 번의 상호작용을 수행하면 원 그래프로부터 관계를 더 잘 인식할 수 있는 관계 인식(Relation aware) 엔티티 결과(즉, )를 얻을 수 있다. 그림 5는 두번의 상호작용을 수행한 내용을 묘사한 그림이다.
3.4 그래프 합성곱 신경망 단계
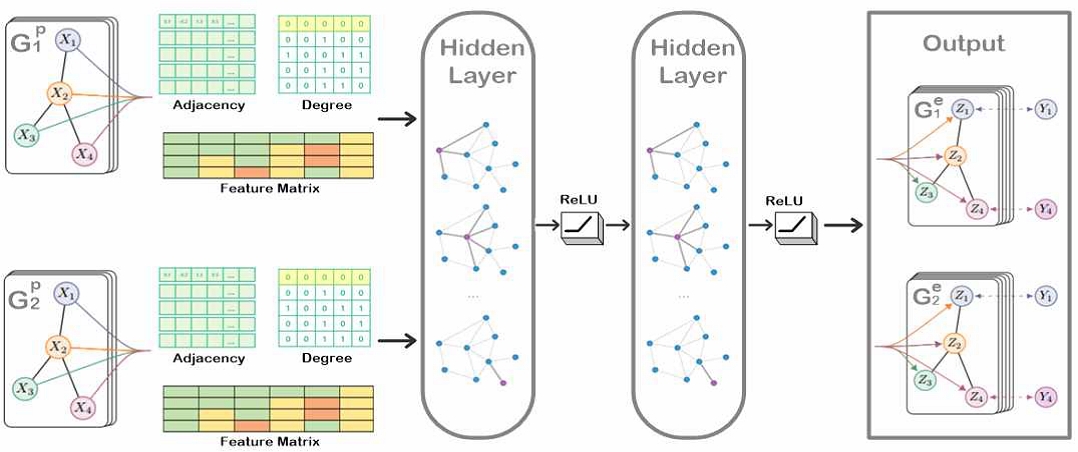
개선된 관계 인식 엔티티 결과는 GCN 모델에 전달되어 합성곱 계층(Convolutional layer)을 통해 최종 결과가 산출된다. 그림 6은 본 연구에서 사용한 GCN 모델의 개념적 구조를 나타낸 것이다. 인접 행렬(Adjacency matrix)과 디그리 행렬(Degree matrix), 그리고 특성 행렬(Feature matrix)은 그래프 합성곱 모델의 입력으로 사용된다.
원 그래프의 최종 출력 형태 는 N개의 노드를 가지는 그래프 G로 표현될 수 있다. 각 그래프는 G = (A, X)로 표기되며, 원자 간의 연결을 나타내는 인접 행렬 A와 개별 원자의 속성을 나타내는 특성 행렬 X로 표현되고, 그래프 합성곱 층의 연산은 다음과 같다.
| (12) |
히든 상태(Hidden state) H(l)은 l번째 그래프 합성곱 층의 결과를 나타내며, 는 단위 행렬 I가 추가된 인접 행렬이고, 는 의 차수 행렬이다. W(l-1)은 (l-1)번째 층의 가중치 행렬이며, η는 활성화 함수 ReLU이다.
게이트 생략 연결(Gated skip connection)[13]은 은닉층을 지나지 않은 히든 상태와 은닉층을 거친 후 배치 정규화를 거친 히든 상태의 상관계수를 계산하여 새로운 히든 상태를 만든다.
| (13) |
여기서, U1과 U2는 선형 은닉층(Linear hidden layer)이고, b는 편향(Bias)을 의미한다. σ는 sigmoid 함수이다. 게이트를 통해 계산된 결과는 sigmoid 활성화 함수를 통해 l층의 히든 상태를 만든다.
| (14) |
마지막으로 GCN 계층으로부터 산출되는 최종 엔티티 결과를 이용하여 두 개체(즉, KG1으로부터 e1과 KG2로부터 e2) 사이의 거리 d(e1,e2)를 식 (15)와 같이 측정한다.
| (15) |
모델 학습을 위해서는 긍정(Positive)뿐만 아니라 부정(Negative) 샘플링이 필요하고 본 연구에서는 부정 샘플링을 수행하였다. 제안 모델의 목적 함수는 식 (16)과 같다.
| (16) |
여기서, margin은 1로 설정하였으며 학습은 손실을 최소화하는 방향으로 수행된다.
이상 본 논문에서 제안하는 GCN과 임베딩 기법을 활용한 엔티티 매칭 수행 방법을 정리 요약하면 그림 7과 같다.
Ⅳ. 실험 분석
본 논문에서 제안하는 지식 그래프 엔티티 매칭 방법의 성능을 분석하기 위해 여러 가지 실험을 수행하였다. 이를 위해 기존 최신의 엔티티 매칭 방법들과 우리의 매칭 방법을 비교⋅분석하였다. 본 실험에서는 실질적이고 의미 있는 결과를 얻기 위해 지식 그래프 분석에서 가장 널리 사용되는 DBP15K 데이터셋을 사용하였다. DBP15K는 영어(En), 중국어(Zh), 프랑스어(Fr), 그리고 일본어(Ja) 4개의 언어로 구성되어 있으며 각 데이터셋에는 약 40,000개 정도의 엔터티가 포함되어 있다. 표 1은 DBP15K 데이터셋에 대한 내역을 보여주고 있다.
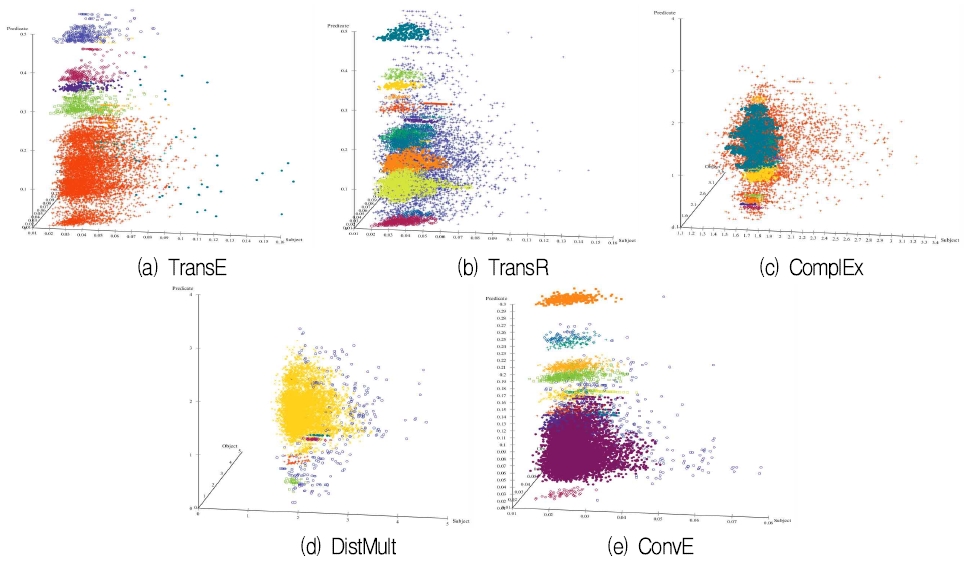
본 장에서는 DBP15K 데이터셋을 사용하여 임베딩 모델들의 성능을 실험⋅분석한다. 그림 8은 모든 데이터를 임베딩시켜 3차원 공간으로 변환시킨 그림이다. TransE와 TransR 클러스터링 성능이 다른 모델보다 직관적으로 우수한 것을 보여주고 있다.
우리는 클러스터링 효과를 평가하기 위해 SC(Silhouette Score) 벤치마크를 채택한다. 여기서 응집력(Cohesion)은 클래스 내 샘플 간의 근접 정도를 반영하고 분리력(Separation)은 클래스 외부 샘플 간의 근접 정도를 반영한다. SC는 식 (17)과 같이 응집력(C)과 분리력(S)으로 계산되며 SC의 범위는 -1에서 1까지이고, 값이 클수록 클러스터링 효과가 좋다.
| (17) |
4.1 임베딩 및 클러스터링 실험 분석
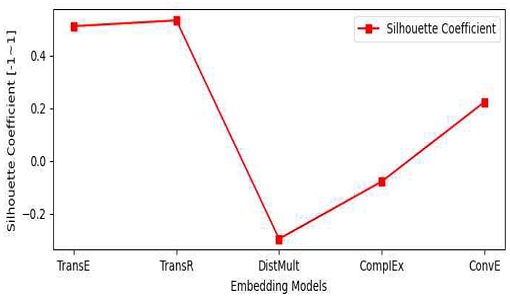
그림 9는 SC 측정값을 그래프로 표현하고 있는데, TransE와 TransR의 성능이 우수하고 그 뒤로 ConvE와 ComplEx, 그리고 DistMult가 가장 성능이 나쁘다. 이들 중 TransR이 가장 우수한 것으로 평가된다.
4.2 엔티티 매칭 실험 분석
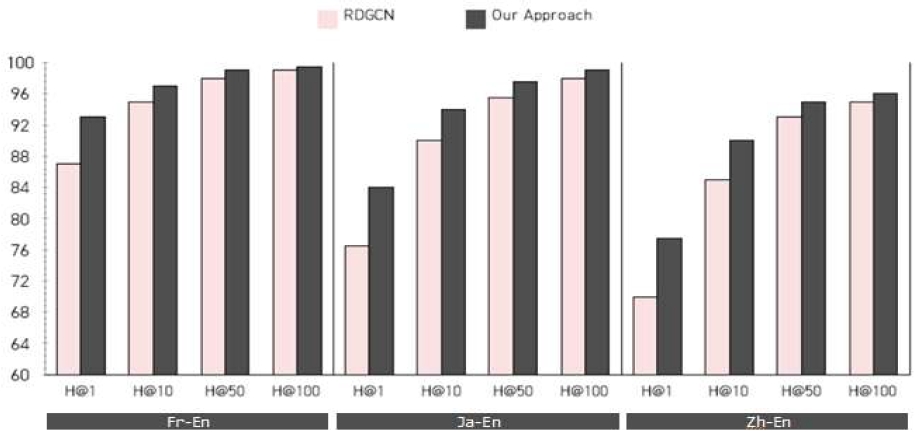
실험은 다음과 같이 수행되는데, 먼저 2개의 지식 그래프 엔티티들이 정확히 일치하는지 평가하기 위해 매칭 평가에서 가장 보편적으로 사용되고 있는 Hit@k 점수를 사용한다. Hit@k는 매칭 결과 상위 k-list 안에 올바른 정답을 찾았는지에 대한 비율을 나타낸다. 그림 10은 기존에 가장 성능이 좋은 방법으로 알려진 RDGCN과 우리의 매칭 방법을 비교한 Hit@k 결과를 보여주고 있다. 세로축은 매칭 확률(단위: %)을 가로축은 Fr-En, Ja-En, Zh-En 데이터셋에 대한 Hit@k(단위: k=1, 10, 50, 100)를 나타낸다. 엔티티 매칭을 한 번에 찾은 Hit@1에서 Zh-En은 10.7%, Ja-En은 9.8%의 성능 향상을 보여주었다. Hit@10에서는 Zh-En이 5.9%, Ja-En이 4.4% 향상을 보였다. 그러나 Hit@50과 Hit@100에서는 큰 향상은 보이지 않고 약간의 증가만 나타내고 있다.
Ⅴ. 결 론
대규모 지식 그래프를 위한 엔티티 매칭 연구에서 가장 어려운 이슈들 중 하나가 서로 다른 라벨링을 사용하는 어휘 이질성 문제이다. 본 논문에서는 이를 해결하기 위해 그래프 합성곱 신경망에 임베딩 기법을 함께 적용한 하이브리드 엔티티 매칭 방법을 제안하였다. 제안된 매칭 방법은 전처리 단계, 임베딩 매칭 단계, 관계 인식 단계, 그리고 그래프 합성곱 신경망 단계로 구성되어 있다.
하이브리드 엔티티 매칭 방법은 기존 최신의 엔티티 매칭 방법들과 성능을 비교⋅분석하였다. 실험 결과 Hit@1에서 Zh-En은 10.7%, Ja-En은 9.8%의 성능 향상을 보여주었고, Hit@10에서는 Zh-En이 5.9%, Ja-En이 4.4% 향상을 보였다. 또한 Hit@50과 Hit@100에서는 큰 향상은 보이지 않았지만 약간의 증가를 보여주고 있다.
Acknowledgments
이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2016R1D1B02008553). 본 논문은 교육부 및 한국연구재단의 4단계 BK21 사업(경북대학교 컴퓨터학부 지능융합 소프트웨어 교육연구단)으로 지원된 연구임 (4199990214394)
References
-
X. Zeng, J. Chang, Y. Lai, and C. Huang, "The current situation and future trend of Big Data: Visualization analysis of literature based on citespace", The 5th International Conference on Big Data and Education(ICBDE), pp. 368-378, Feb. 2022.
[https://doi.org/10.1145/3524383.3524423]

-
J. Kim and Y. Lee, "Design and implementation of extended GCN model for knowledge graph entity matching", Journal of KIIT, Vol. 20, No. 1, pp. 31-39, Jan. 2022.
[https://doi.org/10.14801/jkiit.2022.20.1.31]

-
T. Mikolov, K. Chen, G. Corrado, and J. Dean, "Efficient estimation of word representations in vector space", International Conference on Learning Representations(ICLR), Arizona, USA, Sep. 2013.
[https://doi.org/10.48550/arXiv.1301.3781]

-
M. Busta, L. Neumann, and J. Matas, "FASText: Efficient unconstrained scene text detector", The IEEE International Conference on Computer Vision (ICCV), pp. 1206-1214, Dec. 2015.
[https://doi.org/10.1109/ICCV.2015.143]

-
L. Wu, A. Fisch, S. Chopra, K. Adams, A. Bordes, and J. Weston, "StarSpace: Embed all the things," The Thirty-Second AAAI Conference on Artificial Intelligence, pp. 5569-5577, Sep. 2017.
[https://doi.org/10.48550/arXiv.1709.03856]

-
M. Chen, Y. Tian, M. Yang, and C. Zaniolo, "Multilingual knowledge graph embeddings for cross-lingual knowledge alignment", The International Joint Conference on Artificial Intelligence(IJCAI-17), Melbourne Australia, pp. 1511-1517, Aug. 2017.
[https://doi.org/10.24963/ijcai.2017/209]

-
H. Zhu, R. Xie, Z. Liu, and M. Sun, "Iterative entity alignment via joint knowledge embeddings", The 26th International Joint Conference on Artificial Intelligence(IJCAI-17), Melbourne Australia, pp. 4258-4261, Aug. 2017.
[https://doi.org/10.24963/ijcai.2017/595]

-
Z. Wang, Q. Lv, X. Lan, and Y. Zhang, "Cross-lingual knowledge graph alignment via graph convolutional networks", The 2018 Conference on Empirical Methods in Natural Language Processing, pp. 349-357, Jan. 2018.
[https://doi.org/10.18653/v1/D18-1032]

-
M. Schlichtkrull, T. N. Kipf, P. Bloem, R. Bery, I. Titov, and M. Welling, "Modeling relational data with graph convolutional networks", European Semantic Web Conference(ESWC), pp. 593-607, Jun. 2018.
[https://doi.org/10.1007/978-3-319-93417-4_38]

-
F. Monti, O. Shchur, A. Bojchevski, O. Litany, S. Günnemann, and M. M. Bronstein, "Dual-primal graph convolutional networks", arXiv preprint arXiv:1806.00770, , pp. 1-11, Jun. 2018.
[https://doi.org/10.48550/arXiv.1806.00770]

-
Y. Wu, X. Liu, Y. Feng, Z. Wang, R. Yan, and D. Zhao, "Relation-aware entity alignment for heterogeneous knowledge graphs", The 28th International Joint Conference on Artificial Intelligence, pp. 5278-5284, Aug. 2019.
[https://doi.org/10.48550/arXiv.1908.08210]

-
T. Trouillon, C. R. Dance, E. Gaussier, J. Welbl, S. Riedel, and G. Bouchard, "Knowledge graph completion via complex tensor factorization", Journal of Machine Learning Research, Vol. 18, No. 1, pp. 4735-4772, Jan. 2017.
[https://doi.org/10.48550/arXiv.1702.06879]

-
S. L. Smith, P. J. Kindermans, C. Ying, and Q. V. Le, "Don't decay the learning rate, increase the batch size", International Conference on Learning Representations(ICLR), pp. 1-11, Feb. 2018.
[https://doi.org/10.48550/arXiv.1711.00489]


1985년 : 한국과학기술원 정보검색전공(공학석사)
1997년 : 한국과학기술원 컴퓨터공학전공(공학박사)
1998년 8월 ~ 현재 : 경북대학교 IT대학 컴퓨터학부 교수
관심분야 : 링크드 데이터, 시맨틱 웹, 빅데이터, 지식 그래프

2019년 : 경북대학교 IT대학 컴퓨터학부(공학석사)
2022년 : 경북대학교 IT대학 컴퓨터학부(공학박사)
2023년 3월 ~ 현재 : 경북대학교 소프트웨어기술연구소 연구원
관심분야 : 시맨틱 엔터티 매칭, 빅데이터, 머신러닝