전자기적 시뮬레이션을 활용한 마이크로스트립 불연속 소자의 등가회로 추출

Ⅰ. 서 론

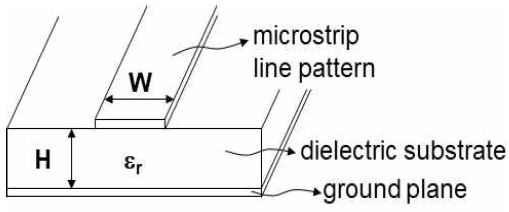
무선통신을 비롯한 각종 무선시스템용 초고주파 회로 설계시 마이크로스트립 선로(Microstrip lines)가 널리 사용되고 있다. 그림 1과 같은 마이크로스트립 선로는 설계나 구성이 편리하고 가격이 낮으며 양산성이 좋다는 장점이 있다. 특히 임의의 마이크로파 회로 패턴을 구현하는데 있어서 타 전송선로에 비하여 우수한 유연성(Flexibility)을 가지고 있고, 외부 섭동구조와 결합하는 것도 용이하다[1][2].

Fig. 1.

Structure of microstrip transmission lines

두께가 H이고 비유전율이 εr인 유전체 기판(Dielectric substrate)이 주어질 경우, 마이크로스트립 전송선로는 선폭 W에 의하여 특성 임피던스(Characteristic impedance, Z_o)가 결정된다. 또는 필요한 Z_o에 해당하는 W를 구하기도 한다. 다만 필요한 전기적 길이만큼 마이크로스트립 선로의 물리적 길이를 구하여 길게 구현하는 것이 기본이다. 그러나 회로의 크기를 줄이거나, 또는 임의의 마이크로파 회로 패턴을 구성하는데 있어서, 선로를 구부리거나 다수 개로 분기시킬 경우가 흔하게 요구된다[3].

마이크로스트립 선로를 구부리거나 2개로 분기시킬 경우 벤드(Bend)와 티(Tee)와 같은 불연속 접합(Junction)이 발생하게 된다. 그러면 불연속 소자에서 마이크로파 신호의 전달은 필연적으로 방해를 받게 되며, 이때 발생하는 기생성분(Parasitic elements)으로 인해 어떤 추가적인 전기적 길이를 갖게 된다[4][5]. 즉, 일직선의 마이크로스트립 선로가 지닌 전기적 길이나 전달특성에 미약하나마 왜곡이 발생하고, 이는 마이크로스트립 선로로 구성되는 마이크로파 회로들의 특성이 나빠지는 결과로 이어진다. 따라서 마이크로스트립 불연속 소자들에 대한 특성을 이해하기 위하여 등가회로를 추출하고 회로 설계시 반영하려는 노력이 오랫동안 이어져 왔다.

마이크로스트립 선로의 불연속 소자에 대한 등가회로 분석을 위하여 종래에는 극히 어렵고 복잡한 전자기 이론이나 다양한 수치해석 방법들이 사용되었다[6][7]. 마이크로파 회로 설계자의 입장에서는 임의의 두께와 비유전율을 갖는 다양한 유전체 기판으로 마이크로스트립 선로 및 마이크로파 회로를 설계한다. 그래서 회로설계시 수시로 사용하는 벤드나 티와 같은 불연속 소자의 등가회로가 필요할 때, 그리고 유전체 기판이 바뀔 때마다 매번 종래의 어려운 방법을 동원해야 한다면 실제로 얻는 실익에 비해 노력, 시간, 비용이 너무 많이 소모된다.

이에 본 연구에서는 회로 설계자의 관점에서 벤드나 티와 같은 마이크로스트립 불연속 소자의 등가회로를 좀 더 쉽게 구하는 방법을 제시한다. 불연속 소자를 포함한 마이크로스트립 선로나 회로 패턴에 대해, 비교적 쉽게 접근할 수 있는 전자기적 시뮬레이션(Electromagentic(EM) simulation)으로 S-파라미터를 구하고, 여기에서 단자 연결 선로(Port feeding line)를 디임베딩으로 제거하면, 불연속 소자만의 특성이 남는다. 여기에 상대적으로 쉬운 회로망 해석법인 Z-파라미터 분석법을 적용하면 불연속 소자의 등가회로를 어렵지 않게 구할 수 있다.

본 연구에서는 등가회로 소자값을 구할 마이크로스트립 불연속 소자의 예로 매우 널리 사용되는 벤드와 티 접합 소자(Junction elements)를 취한다. 각각의 전송특성을 알려주는 S-파라미터를 EM 시뮬레이션으로 구하고, 이로부터 불연속 부분의 등가회로를 구하여 그 특성을 비교한다. 또한, 실제 측정 결과와도 유사성이 있음을 보이기 위하여 샘플 회로를 제작하고 그 전송특성을 측정한다. 결론적으로 세 가지 전송특성을 서로 비교하여 서로 유사함을 보이고, 이로부터 본 연구에서 제안한 마이크로스트립 선로의 불연속 부분에 대한 등가회로 추출 방법이 마이크로파 회로 설계자의 관점에서 타당함을 보이고자 한다.

Ⅱ. 마이크로스트립 불연속 소자

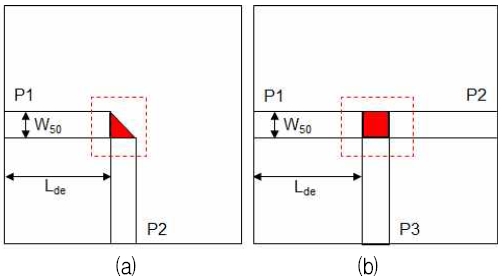
그림 2는 마이크로스트립 선로 또는 마이크로파 회로 패턴에서 가장 널리 사용되는 불연속 소자인 벤드와 티 소자를 보여주고 있다. P1, P2, P3는 각각 단자1(port1), 단자2, 단자3을 의미한다. W₅₀은 본 연구에서 취한 50Ω 마이크로스트립 단자 연결 선로의 폭(W)이다. 길이가 L_de인 일직선의 50Ω 단자 연결 선로는 본 연구에서는 물론이고, 어떠한 형태의 마이크로파 회로에서든 외부와의 연결을 위하여 필요하다. 길이 L_de는 불연속 소자의 등가회로 추출과정에서 제거(De-embedding)된다.

Fig. 2.

Microstrip discontinuity elements (a) Bend (b) Tee

그림 2(a)의 경우, P1에 입사된 마이크로파 신호는 90도로 꺾여서 P2로 전달된다. 그림 2(b)의 경우, P1에 인가된 신호는 P2와 P3로 표시한 단자로 신호가 전달될 것이다. 점선 상자로 표시한 부분이 벤드나 티 형태의 불연속 소자이다.

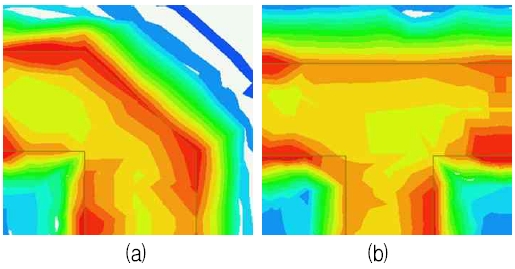
그림 3은 HFSS(High Frequency Structure Simulator)로 마이크로스트립 벤드와 티에 대한 EM 시뮬레이션을 수행한 이후 전기장 분포를 나타낸 것이다.

Fig. 3.

E-field distribution of discontinuity elements (a) Bend (b) Tee

마이크로스트립 선로와 그 주변 유전체를 따라 진행하는 전자기파는 불연속 접합을 만나면 그림 3에 표시한 것처럼 전자기장 분포에 왜곡이 발생한다. 즉, 단순한 일직선 전송선로에서보다 순간적으로 강한 전기장의 왜곡된 분포가 불연속 소자 주변에 나타나는 것이다. 이로 인하여 단순한 직선 선로에는 존재하지 않았던 추가적인 인덕턴스와 커패시턴스가 불연속 부분의 등가회로에 나타나게 된다. 그러면 여기에서 미약하나마, 전달되는 신호의 손실과 입사되는 신호의 반사가 나타나게 된다. 마이크로파 회로 설계자의 관점에서는 이러한 불연속 소자에 대한 등가회로 분석이 마이크로파 회로를 조금이라도 더 정확하게 설계하는데 도움이 된다.

Ⅲ. 불연속 소자의 등가회로와 검증 과정

그림 2의 마이크로스트립 전송선로로 EM 시뮬레이션을 하면, 길이가 L_de인 단자 연결 선로까지 포함한 S-파라미터([S]_em)를 얻게 된다. 그러므로 불연속 소자의 등가회로 추출을 위해서는 단자 연결 선로를 디임베딩하여 제거한 후 불연속 소자만의 S-파라미터([S]_dis)를 남겨야 한다.

그림 4는 단자 연결 선로를 제거하고 불연속 소자만 남기는 경우에 대한 이해를 돕기 위하여 단순화한 그림이다. 여기서 한 가지 주의할 점은, 그림 4에 보인 불연속 소자만을 따로 정의하고 이것의 특성을 시뮬레이션하면 안된다는 것이다. 불연속 소자의 특성은 이것에 연결된 전송선로와 결합되어 함께 나타난다. 그림 4처럼 불연속 소자만을 독립적으로 정의하면 주변 선로와의 상호작용(Interaction)이 없어서 단자 임피던스나 신호의 흐름 등 전기적 특성이 정확하게 시뮬레이션되지 않기 때문이다.

Fig. 4.

Discontinuity parts after de-embedding port feeding lines (a) Bend (b) Tee

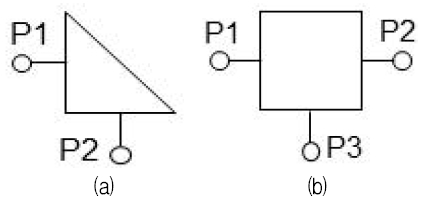
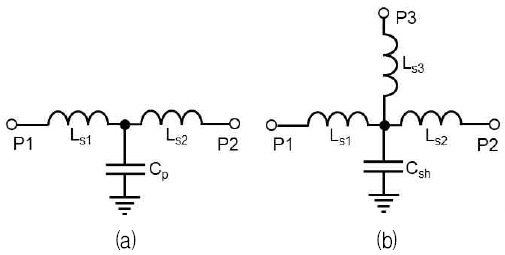
그림 5는 불연속 소자의 등가회로이다. 불연속 소자에서도 마이크로파 신호는 입력단자(예: P1)에서 건너편 단자(예: P2, P3)로 건너가므로 기본적으로 인덕턴스가 존재한다[8]. 그리고 불연속 구간의 모서리, 선로 접합부 근처, 방향이 꺾이는 지점 등에서 주변 유전체층으로 퍼지는 전자기장(Fringing field) 때문에 등가의 션트 커패시터(Shunt capacitor)가 포함되어야 한다. 물론 등가회로 구성시 물리적 해석에 따라 다양한 토폴로지(Topology)가 가능한데, 본 연구에서는 상기에서 설명한 신호의 전달과 프린징 필드를 들어 그림 5의 등가회로를 설정하였다. 불연속 소자의 등가회로 추출은 곧 그림 5의 등가회로 소자값을 찾는 과정이다.

Fig. 5.

Equivalent circuits of the microstrip discontinuity elements (a) Bend (b) Tee

본 연구에서는 마이크로파 회로설계자의 관점에서 등가회로 소자값을 용이하게 추출하기 위하여 EM 시뮬레이션에서 구한 S-파라미터([S]_em)에서 출발한다. [S]_em에서 단자 연결 선로를 디임베딩하면 그림 4에 보인 불연속 소자만의 S-파라미터([S]_dis)가 남는다. [S]_dis는 이미 널리 알려진 변환식에 의하여 [Z]_dis로 쉽게 변환된다[9]. [Z]_dis로부터 그림 5에 보인 등가회로를 추출할 수 있는데, 이 과정은 다음 장에서 별도로 기술하고자 한다.

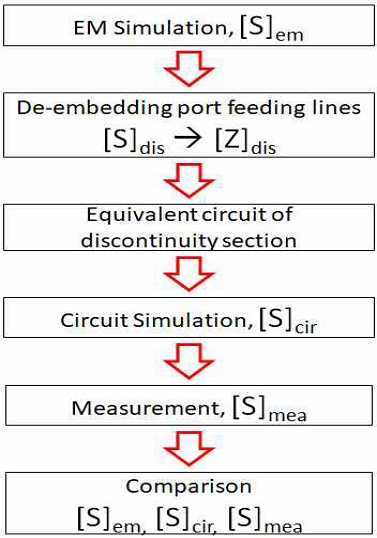
이제 본 연구에서 사용한 등가회로 검증 과정에 대하여 언급하고자 한다. 불연속 소자의 등가회로를 얻은 후 디임베딩했던 단자 연결 선로를 단자 위치에 다시 연결하고 이를 회로 시뮬레이터(Circuit simulator)에서 정의하면 새로운 S-파라미터([S]_cir)를 얻을 수 있다. 이것이 EM 시뮬레이션에서 얻은 S-파라미터([S]_em)와 유사하면 불연속 소자에 대한 등가회로는 믿을 수 있게 된다. 본 연구에서는 실험적으로도 검증하기 위하여 불연속 소자를 포함한 측정용 DUT(Device Under Test)를 실제로 제작하고 그 S-파라미터([S]_mea)를 측정하여 비교하였다. 이상적으로 세 개의 S-파라미터([S]_em, [S]_cir, [S]_mea)이 같아야 하는데, 현실적으로 다소의 오차가 좀 있더라도 유사하게 나오면 좋다. 그림 6은 지금까지 설명한 불연속 소자의 등가회로 추출과 검증 과정을 간단하게 정리한 흐름도이다.

Fig. 6.

Verification steps of the equivalent circuits for the discontinuity elements

Ⅳ. 회로망 분석법을 이용한 등가회로 추출

본 장에서는 간단한 회로망 분석법을 이용하여 불연속 소자의 등가회로를 추출한다. 본 연구에서는 매우 어렵고 복잡한 전자기장 이론이나 수치해석 방법에 의존하지 않고, 회로 설계자들이 쉽게 접근할 수 있도록, 상대적으로 쉽고 간단한 회로망 해석법으로 등가회로 소자값을 구한다.

4.1 마이크로스트립 벤드

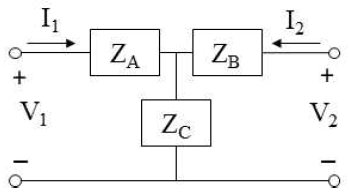
그림 7은 Z-파라미터로 2단자 회로망을 해석하기 위하여 사용되는 블록도로서, 더 이상의 부연 설명이 필요없을 정도로 널리 알려진 회로도이다[10]. 매우 쉽고도 단순한 2단자 회로망 해석법에 따라 단자전압을 정의하면 식 (1)과 같다.

$\[ V_1=Z_{11}{I}_1+Z_{12}{I}_2 \]$

(1a)

$\[ V_2=Z_{21}{I}_1+Z_{22}{I}_2 \]$

(1b)

Fig. 7.

2-port Z-parameter network for extracting the equivalent circuit of microstrip bend

이제 각 단자의 개방 및 단락을 통해 2단자 Z-파라미터 식을 정리하면 식 (2)와 같은데, 이것이 곧 마이크로스트립 벤드 불연속 소자의 [Z]_dis이다.

$\[ Z_{11}=\frac{V_1}{I_1}\left|{}_{I_2=0}\right.=Z_A+Z_C \]$

(2a)

$\[ Z_{12}=\frac{V_1}{I_2}{\left|\right.}_{I_1=0}=Z_C \]$

(2b)

$\[ Z_{21}=\frac{V_2}{I_1}{\left|\right.}_{I_2=0}=Z_C \]$

(2c)

$\[ Z_{22}=\frac{V_2}{I_2}{\left|\right.}_{I_1=0}=Z_B+Z_C \]$

(2d)

그러면 간단한 ZA, ZB, ZC는 식 (3)과 같게 된다.

$\[ Z_A=Z_{11}-Z_{12} \]$

(3a)

$\[ Z_B=Z_{22}-Z_{21} \]$

(3b)

$\[ Z_C=Z_{12} \]$

(3c)

이를 그림 5(a)에 적용하면 세 개의 등가회로 소자값들이 식 (4)와 같이 쉽게 추출된다.

$\[ L_{s1}=-\frac{Im\left(Z_{11}\right)-Im\left(Z_{12}\right)}{\omega } \]$

(4a)

$\[ L_{s2}=-\frac{Im\left(Z_{22}\right)-Im\left(Z_{21}\right)}{\omega } \]$

(4b)

$\[ C_p=\frac{1}{\omega \times Im\left(Z_{12}\right)} \]$

(4c)

4.2 마이크로스트립 티

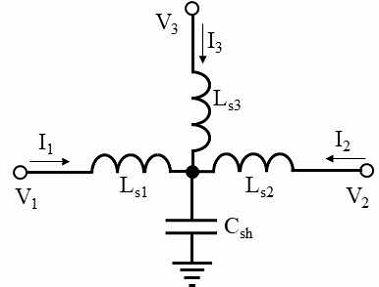
그림 8은 그림 5(b)에 보인 마이크로스트립 티의 등가회로를 얻기 위하여 단자 전압과 전류를 정의한 그림이다. 여기에서도 역시 널리 알려진 회로망 해석법인 키르히호프의 전압법칙을 이용하면 상대적으로 쉽게 등가회로를 추출할 수 있다[11]. 식 (5)는 세 단자에서의 전압식을 정리한 것이다.

$\[ V_1=j\omega L_{s1}{I}_1+\frac{1}{j\omega C_{sh}}\left[I_1+I_2+I_3\right] \]$

(5a)

$\[ V_2=j\omega L_{s2}{I}_2+\frac{1}{j\omega C_{sh}}\left[I_1+I_2+I_3\right] \]$

(5b)

$\[ V_3=j\omega L_{s3}{I}_3+\frac{1}{j\omega C_{sh}}\left[I_1+I_2+I_3\right] \]$

(5c)

Fig. 8.

3-port equivalent circuit of the microstrip Tee

이들을 행렬식으로 간단히 정리하면 식 (6)과 같은데, 3단자 Z-파라미터 행렬식이 바로 마이크로스트립 티 불연속 소자의 [Z]_dis가 된다.

$\[ \left[\begin{array}{c}\begin{array}{c}{V}_1\\ V_2\end{array}\\ V_3\end{array}\right]=j\left[\begin{array}{ccc}\omega {Ls}_1-\frac{1}{\omega C_{sh}}& -\frac{1}{\omega C_{sh}}& -\frac{1}{\omega C_{sh}}\\ -\frac{1}{\omega C_{sh}}& \omega L_{s2}-\frac{1}{\omega C_{sh}}& -\frac{1}{\omega C_{sh}}\\ -\frac{1}{\omega C_{sh}}& -\frac{1}{\omega C_{sh}}& \omega L_{s3}-\frac{1}{\omega C_{sh}}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{I}_1\\ I_2\end{array}\\ I_3\end{array}\right] \]$

(6a)

$\[ \left[\begin{array}{c}\begin{array}{c}{V}_1\hfill \\ V_2\hfill \end{array}\hfill \\ V_3\hfill \end{array}\right]=\left[\begin{array}{ccc}{Z}_{11}\hfill & Z_{12}\hfill & Z_{13}\hfill \\ Z_{21}\hfill & Z_{22}\hfill & Z_{23}\hfill \\ Z_{31}\hfill & Z_{32}\hfill & Z_{33}\hfill \end{array}\right]\left[\begin{array}{c}\begin{array}{c}{I}_1\hfill \\ I_2\hfill \end{array}\hfill \\ I_3\hfill \end{array}\right] \]$

(6b)

이제 식 (6)으로부터 네 개의 등가회로 소자값들을 식 (7)을 이용해 쉽게 계산할 수 있다.

$\[ L_{s1}=-\frac{Im\left(Z_{11}\right)-Im\left(Z_{12}\right)}{\omega } \]$

(7a)

$\[ L_{s2}=-\frac{Im\left(Z_{22}\right)-Im\left(Z_{21}\right)}{\omega } \]$

(7b)

$\[ L_{s3}=-\frac{Im\left(Z_{33}\right)-Im\left(Z_{13}\right)}{\omega } \]$

(7c)

$\[ C_{sh}=\frac{1}{\omega \times Im\left(Z_{12}\right)} \]$

(7d)

Ⅴ. 등가회로 추출 및 검증 결과

본 연구에서는 제안한 등가회로 추출방법을 실제로 적용해 보기 위하여 비유전율(ε_r)이 4.4이고 두께가 0.78㎜인 유전체 기판을 이용하여 그림 2에 보인 마이크로스트립 벤드와 티를 설계하였다. 단자 연결 선로인 50Ω 선로의 폭(W₅₀)와 길이(L_de)는 각각 1.48㎜, 10㎜이다.

먼저 HFSS로 그림 2의 구조에 대하여 EM 시뮬레이션을 하여 3㎓까지의 [S]_em을 얻었다. 그리고 각 단자의 연결 선로를 디임베딩하여 불연속 소자만의 [S]_dis를 얻었다. [S]_dis를 [Z]_dis로 변환하여 위의 설명대로 그림 5의 등가회로 소자값들을 구한 결과, 마이크로스트립 벤드의 경우, L_s1(=L_s2)는 0.1564nH, C_p는 0.2694㎊이었다. 마이크로스트립 티의 경우, L_s1(=L_s2)는 0.0646nH, L_s3는 0.7666nH, C_sh는 0.0369㎊이었다.

이제 그림 5의 등가회로에 50Ω 단자 연결 선로 10㎜를 연결하고, 회로 시뮬레이터인 ADS(advanced design system)로 [S]_cir를 구하여 [S]_em과 비교하였다. 또한, 본 연구에서는 마이크로스트립 불연속 소자를 직접 제작하고, 그 전기적 특성인 [S]_mea를 측정하여 [S]_em, [S]_cir과 비교하였다. 그림 9는 직접 제작한 마이크로스트립 벤드와 티 회로들을 보여주고 있다. 대학 실험실 보유 설비에 의한 수작업(in-house fabrication) 결과라서 비교 주파수를 비교적 낮은 마이크로파 대역인 3GHz까지 취하였다.

Fig. 9.

Photos of the fabricated circuits (a) Bend (b) Tee

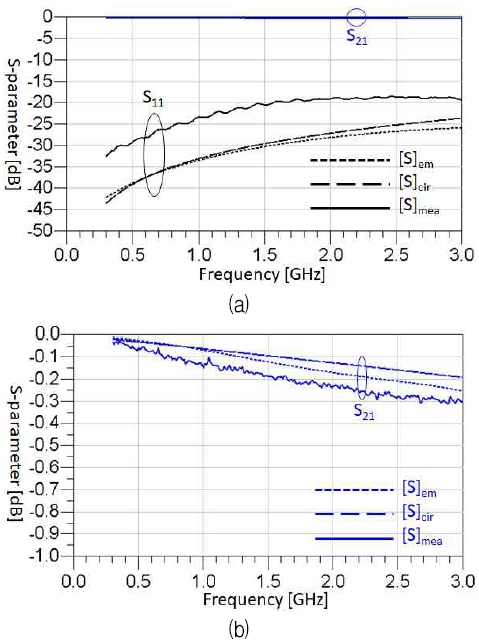
그림 10은 마이크로스트립 벤드에 대한 세 가지 S-파라미터를 비교한다. 신호 전달과 반사계수에 있어서 제안한 방법으로 얻은 등가회로의 S-파라미터가 처음 EM 시뮬레이션과 잘 일치하고 있음을 알 수 있다. 따라서 제안한 등가회로 추출 방법이 매우 타당함을 알 수 있다. 그리고 측정을 통하여 얻은 S-파라미터도 초고주파 영역에서 비교적 유용한 결과를 보여주고 있다.

Fig. 10.

S-parameters of the microstrip Bend (a) S11 and S21 (b) Magnified plot of S21

다만, 반사계수(S₁₁) 특성에 관하여 추가적으로 언급되어야 할 점이 있다. 측정 결과가 EM 시뮬레이션 결과와 다소 오차가 있는 것처럼 보이지만, -20dB 이하의 반사계수에서는 마이크로파 신호의 크기에 미세한 차이만 있어도 로그 스케일 비교에서 큰 차이가 있는 것처럼 보인다는 점을 생각하면 큰 의미를 부여할 수 없는 오차이다. 또한 수작업에 의한 회로 에칭 및 솔더링(Soldering)의 오차 유발 요인도 측정결과에 들어가 있음을 고려해야 한다. 오히려, -20dB 정도의 반사계수는 입사전력의 1/100 이하가 반사되므로 신호 전달 특성이 우수함을 의미하고, 그래서 반사계수 특성 그래프의 전체적인 추세가 유사한 것이 더 중요하다. 측정에서 발생한 오차는 더 정밀한 회로 에칭 및 제작 과정을 통하여 충분히 극복되어야 할 사항이다.

따라서 제안한 방법에 의한 등가회로의 S-파라미터가 EM 시뮬레이션 결과와 유사하다는 점이 더 강조되어야 한다.

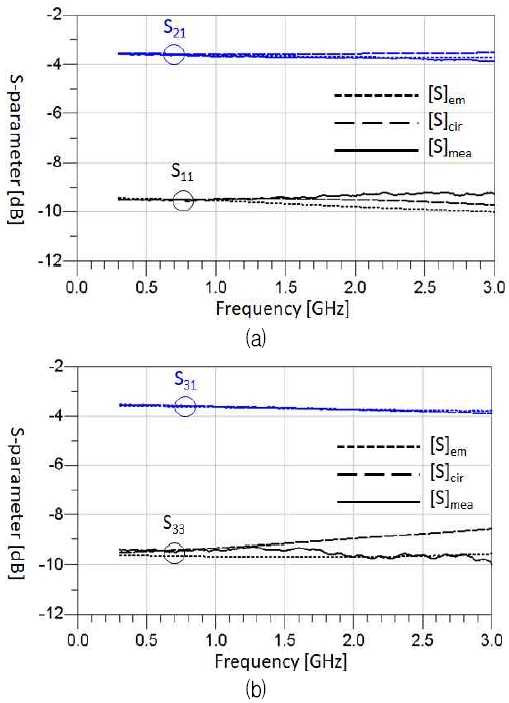
그림 11은 마이크로스트립 티에 대한 S-파라미터를 보여주고 있다. 마이크로스트립 티 구조가 정밀한 초고주파 전력분배기 회로는 아니지만, 3-단자 회로이므로 편의상 신호의 전달(S₂₁, S₃₁)과 및 단자의 반사계수(S₁₁, S₃₃)를 비교하였다. EM 시뮬레이션과 등가회로에서 구한 S-파라미터가 비교적 유사한 특성을 보이고 있으므로, 제안한 방법으로 구한 등가회로가 타당함을 보이고 있다. 또한 측정으로 구한 S-파라미터도 크게 어긋나지 않고 비슷한 특성을 보인다.

Fig. 11.

S-parameters of the microstrip Tee (a) S11 and S21 (b) S33 and S31

본 연구에서 사용한 FR-4 기판은 우수한 양산성과 저가격으로 비교적 낮은 초고주파 대역에서 산업적으로 매우 널리 사용되고 있다. 그러나 마이크로파 특성 관점에서 보면 비교적 손실이 많은 유전체 기판인데, 본 연구에서도 측정 주파수 대역의 높은 영역에서는 조금씩 손실이 커지고 있음이 확인된다.

즉, 주파수가 높아질수록 도체 손실, 유전체 손실, 방사 손실 및 기타 정확한 예측이 어려운 여러 가지 불확실성 요인(Uncertainty factors) 등이 나타나기 시작하고 특성이 나빠진다. 그러므로 EM 시뮬레이션과 이를 기반으로 한 회로망 분석에 의한 본 연구 결과가 높은 주파수에서 갖는 한계라고도 이해된다. 그럼에도 불구하고 마이크로파 회로 설계자의 관점에서는, 사용하는 유전체 기판의 주파수 특성이 어느 정도 확보되는 주파수 범위 내에서는, 매우 간단한 회로망 해석법으로도 불연속 소자의 등가회로를 충분히 예측할 수 있다는 장점이 있다.

Ⅵ. 결 론

본 연구에서는 마이크로파 회로에서 널리 사용되는 마이크로스트립 선로의 벤드와 티 불연속 소자의 등가회로 추출에 대하여 언급하였다.

극히 어려운 전자기 수식이나 수치해석 방법에 의존했던 기존 방법 대신에, EM 시뮬레이션으로 쉽게 구할 수 있는 S-파라미터를 기반으로 마이크로파 회로 설계자가 사용하기 쉬운 Z-파라미터 회로망 분석법을 적용하여 등가회로를 구하였다.

단자와 불연속 소자 사이에 연결되는 연결 선로를 디임베딩한 후 불연속 소자 부분만의 S-파라미터를 Z-파라미터로 변환하는 손쉬운 관계식을 이용하여 등가회로를 추출하였다. 등가회로를 검증하기 위하여 추출된 등가회로에 단자 연결 선로를 연결하여 회로 시뮬레이션을 실시하였고, 이를 EM 시뮬레이션에서 구한 S-파라미터와 비교하여 3GHz 대역의 마이크로파 주파수까지 잘 일치함을 보였다.

실험적으로도 검증하기 위하여, 연구개발용이나 산업생산용으로 폭넓게 사용되는 FR-4 기판으로 마이크로스트립 벤드와 티 회로를 제작하고 S-파라미터 특성을 실제로 측정하였다. 대학 실험실 수준의 제작 설비와 수작업에 의한 회로 제작으로 의하여 제작한 회로 및 측정한 S-파라미터의 정밀도가 다소 떨어질 수 있음에도 불구하고, EM 시뮬레이션 및 등가회로에서 구한 S-파라미터들과 유사함을 확인하였다. 따라서 마이크로파 회로 설계자의 관점에서 제안된 등가회로 추출방법의 타당성이 충분히 검증되었다고 할 수 있다.

본 연구에서 제안된 등가회로 추출방법은 어렵고 복잡한 전자기 방정식이나 수치해석 방법이 아니더라도, 누구나 쉽게 사용가능한 전자기 시뮬레이터와 학부생 수준의 회로망 해석 능력만 있어도 충분히 등가회로를 얻을 수 있다는 장점이 있다. 따라서 수 GHz대의 비교적 낮은 대역의 마이크로파 주파수라면 회로설계자의 관점에서 충분히 사용 가능한 방법이라 할 수 있다. 제안된 등가회로 추출방법은 어떠한 형태의 마이크로스트립 전송선로의 불연속 소자에 대해서라도 비슷한 개념과 검증 과정으로 적용이 가능할 것이라고 기대된다.

Acknowledgments

본 연구는 2022년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신사업(2021RIS-004)과 순천향대학교의 지원으로 수행하였음

References

• K. C. Gupta, R. Garg, I. Bahl, and P. Bhartia, Microstrip Lines and Slotlines(2/e), Ch. 1 and Ch. 2, Artech House, MA, pp. 1-6, 1996.
• J. Lim, W. S. Yoon, S. H. Son, S. M. Han, and D. Ahn, "Design of Size-Reduced Power Dividers Using Both Inductive and Capacitive Perturbation Structures", Journal of KIIT, Vol. 18, No. 6, pp. 65-72, Jun. 2020. [https://doi.org/10.14801/jkiit.2020.18.6.65]
• B. C. Wadell, Transmission Line Design Handbook, Ch. 5, Artech House, MA, 1991.
• W. Menzel and I. Wolff, "A Method for Calculating the Frequency-Dependent Properties of Microstrip Discontinuities", IEEE Transactions on Microwave Theory and Techniques, Vol. 25, No. 2, pp. 107-112, Feb. 1977. [https://doi.org/10.1109/TMTT.1977.1129049]
• S. C. Wu, H. Y. Yang, N. Alexopoulos, and I. Wolff, "A Rigorous Dispersive Characterization of Microstrip Cross and T Junctions", IEEE Transactions on Microwave Theory and Techniques, Vol. 38, No. 12, pp. 1837-1844, Dec. 1990. [https://doi.org/10.1109/22.64564]
• V. Rizzoli, "A General Approach to the Resonance Measurement of Asymmetric Microstrip Discontinuities", 1980 IEEE MTT-S International Microwave Symposium Digest, pp. 422-424, May 1980. [https://doi.org/10.1109/MWSYM.1980.1124308]
• P. Silvester and P. Benedek, "Microsttrip Discontinuity Capacitance for Right-abgle Bends, T-junctions and Crossings", IEEE Transactions on Microwave Theory and Techniques, Vol. 21, No. 5, pp. 341-346, May 1973. [https://doi.org/10.1109/TMTT.1973.1127992]
• A. Thomson and A. Gopinath, "Calculation of Microstrip Discontinuity Inductances", IEEE Transactions on Microwave Theory and Techniques, Vol. 23, No. 8, pp. 648-655, Aug. 1975. [https://doi.org/10.1109/TMTT.1975.1128643]
• D. M. Pozar, Microwave Engineering(4/e), Ch. 4, John Wiley and Sons, Inc., New York, pp. 188-194, 2011.
• W. Hayt, J. Kemmerly, and S. Durbin, Engineering Circuit Analysis(8/e), Ch. 17, McGraw-Hill, New York, pp. 708-712, 2007.
• W. Hayt, J. Kemmerly, and S. Durbin, Engineering Circuit Analysis(8/e), Ch. 3, McGraw-Hill, New York, pp. 40-46, 2007.