유한기억 필터 기반 DPLL 최적설계
초록
DPLL(Digital Phase-Locked Loop)은 기본 회로로서 디지털 검출기, 디지털 루프 필터, 전압 제어 발진기, 분배기 등으로 구성된 회로 중 하나로 전기 및 회로 분야 등 많은 분야에서 널리 사용되고 있다. DPLL 성능 향상을 위해 디지털 루프 관련 연구가 활발히 수행되고 있으며, 수학적 알고리즘인 IIR(Infinite Impulse Response) 기반의 상태 추정기가 사용된다. 본 논문에서는 FIR(Finite Impulse Pulse Response) 상태 추정기 기반의 DPLL을 제안하며 기존의 오차 공분산을 갖는 최적의 FIR 필터보다 부정확한 상황에서 강인한 성능을 갖는 Frobenius 놈 기반 상태추정기 기반 DPLL을 제안한다. Frobenius 놈 기반 FIR 필터는 이득의 크기를 최소화 하는 방법으로 외란의 강인한 성능을 지니며, 본 논문에서는 Frobenius 놈 이득을 최적화하기 위해 수치적 방법을 제안한다. 시뮬레이션에서 기존 DPLL과의 성능 비교를 통해 제안한 DPLL의 우수한 성능을 검증한다.
Abstract
The digital phase-locked loop(DPLL) is one of the circuits composed of a digital detector, digital loop filter, voltage controlled oscillator, divider, and etc. as a fundamental circuit, widely used in many fields such as electrical and circuit fields. In order to improve the performance of the DPLL, research has been conducted to improve the performance of the digital loop of the DPLL. An infinite impulse response(IIR) state estimator, which is a mathematical algorithm, is used as one of various methods for improving performance. In this paper, we propose a DPLL based on FIR(Finite Impulse Pulse Response) state estimator. A DPLL using the Frobenius norm-based state estimator, which has more robust performance in inaccurate situations than the minimum variance FIR filter. The Frobenius norm-based FIR filter has robust performance against disturbances by minimizing the norm of the gain, and in this paper, we propose a numerical method to optimize the Frobenius norm gain. The superior performance of the new DPLL is verified through performance comparison with the existing DPLL through simulation.
Keywords:
frobenius norm, DPLL, kalman filter, FIR filter, unbiased conditionⅠ. 서 론
디지털 위상 고정루프(DPLL, Digital Phase-Locked Loop)는 디지털 위상 검출기, 디지털 루프 필터, 디지털 제어 발진기, 분배기 등으로 이루어진 일반적인 회로로 통신, 제어 신호처리 등 다양한 분야에서 널리 사용된다[1]. 디지털 위상 고정루프의 성능을 향상시키기 위해 많은 연구들이 진행되어 왔으며, 하드웨어의 발전 및 집적화, 다양한 수학적 알고리즘 기반 소프트웨어의 향상 등 다양한 방면에서 디지털 위상 고정루프의 성능을 발전시켜왔다[1]-[2]. 디지털 위상 고정루프를 설계하는 가장 간단한 방법은 고정된 이득값을 갖는 디지털 루프를 설계하는 방법으로 간단하며 가격이 저렴한 장점이 있다[2]. 하지만, 디지털 루프의 이득값을 고정하면 외란이나 파라미터 변화 시 성능저하가 발생할 수 있다. 디지털 위상 고정루프의 루프 필터 성능향상을 위해 수학적 알고리즘을 적용하였는데, 대표적으로 칼만 필터(Kalman filter)가 사용되었으며, 칼만필터 기반의 디지털 위상 고정루프의 강인성 향상을 위해 듀얼 루프 구조를 갖는 칼만 필터도 개발되었다[3].
칼만 필터는 우수한 성능을 가진 상태추정기로 잡음이 포함되어 있는 측정치로부터 상태변수를 추정하는 알고리즘이다. 칼만 필터는 컴퓨터 비전, 로봇공학, 회로, 제어, 신호처리 등 다양한 분야에서 활용되어왔다. 최근 우수한 성능을 바탕으로 수중 탐사 로봇의 측위[4] 비행선 공기 역학 모델 추정[5], 3차원 공간에서 무인 항공체의 고도 추정[6], 무인 항공체의 위치 추정 및 충돌 회피[7] 등 다양한 분야에서 활용되었다. 하지만 칼만 필터는 이상적인 환경에서 우수한 성능을 보이지만 무한 임펄스 응답 필터(IIR filter, Imfinite impulse response filter)구조를 갖기 때문에 예측하지 못한 상황에서 급격한 성능저하를 보이거나 발산하는 등의 현상이 발생할 수 있다. 또한, 확장 칼만필터, 무향 칼만 필터, 파티클 필터 등 다양한 연구들이 존재하는데 모두 오차 발생 시 오차가 누적되는 무한 응답 임펄스 구조의 특성으로 평소에는 우수한 성능을 보이지만, 오차의 누적으로 인한 급격한 성능저하가 발생할 수 있는 구조적 한계를 지니고 있다. 오차 누적을 막기 위해 유한 임펄스 응답 필터(FIR filter, Finite Impulse Response filter)가 사용된다.
유한 응답 상태추정기는 유한 입력 유한 출력 안정성(BIBO stability, Bounded Input Bounded Output stability)을 가져 우수한 성능을 보인다[8][9]. 우수한 추정성능을 바탕으로 최적의 유한 임펄스 응답 필터, 편향되지 않은 유한 임펄스 응답 필터, 프로베니우스 놈 유한 임펄스 응답 필터 등 다양한 유한 임펄스 응답 필터가 연구되어왔으며, 실내 위치 추정, 드론의 제어 및 측위, 영상처리 등 많은 분야에서 연구가 진행되어왔다[9]-[14]. 유한 임펄스 응답 필터는 최근의 측정값을 사용하여 추정하는데, 이때 최근 측정값의 길이(Horizon size)가 중요한 파라미터 중 하나이다. 짧은 측정값의 길이는 빠른 연산속도를 갖지만 잡음과 외란을 억제하기 어려우며 너무 긴 측정값 구간은 잡음과 외란을 억제하지만 연산량 증가가 발생할 수 있어 적절한 측정값의 길이를 선정하는 방법이 중요하다.
본 논문에서는 프로베니우스 놈 FIR 필터 기반 디지털 위상 고정루프를 제안한다. 기존 FIR 필터는 최적의 에러 공분산을 갖지만 프로베니우스 놈 기반 FIR 필터는 이득값의 크기를 최소화하여 측정값의 외란으로부터 우수한 성능을 지니는 특징을 가지고 있기 때문에[9], 본 논문에서는 프로베니우스 놈 FIR 필터 기반 DPLL을 제안한다. 프로베니우스 놈 기반 제안한 디지털 위상 고정루프는 칼만 필터 기반의 디지털 위상 고정루프보다 우수한 성능을 갖는다. 프로베니우스 놈 임펄스 응답 필터 설계에 관한 설명을 위해 상태 공간 모델에 관한 설명 이후 선형 행렬 등식의 해를 구하고, 설계된 프로베니우스 놈 임펄스 응답 필터가 불편성 조건 대해 서술한 후 이득을 구한다. 디지털 위상 고정루프에 두 가지 파라미터에 관하여 서술하며, 두 가지 파라미터를 최적화 하기 위한 방법을 수치적 접근 방법으로 서술하며 기존 수치적 방법에서는 측정값 길이만 구했으나, 본 논문에서는 최적의 행렬이득 가중치도 제안한다. 제안한 프로베니우스 놈 임펄스 응답필터 기반 디지털 위상 고정루프의 우수성을 시뮬레이션을 통해 입증하였다.
본 논문의 구성은 다음과 같다. 2장에서 프로베니우스 놈 임펄스 응답 필터 기반 디지털 위상 고정루프를 설계하고, 3장에서는 제시된 모델을 기반으로 제안한 디지털 위상 고정루프의 강인성을 검증하기 위한 시뮬레이션 결과를 보이며, 4장에서 본 논문의 결론을 맺는다.
Ⅱ. 유한기억 필터 기반 DPLL 최적설계
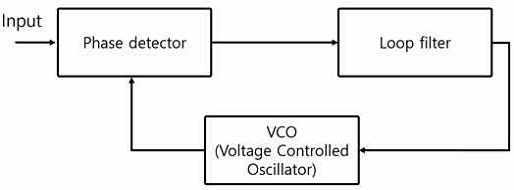
본 장에서는 새로운 디지털 위상 고정루프를 설계하는 방법을 서술한다. 디지털 위상 고정루프는 그림 1과 같이 표현된다.
본 장에서는 새로운 디지털 위상 고정루프를 설계하는 방법을 서술한다. 디지털 위상 고정루프는 그림 1과 같이 표현된다. 본 논문에서는 루프 필터 성능향상 방법을 서술한다. 디지털 위상 고정루프의 루프필터 설계 시 상태 벡터를 xk = [αk βk]T, 영점통과 포인트는 αk = t0+k(T1 - T0), 타이밍 오프셋은βk = T1 - T0, 초기타이밍 오프셋은 t0, 수신기와 발신기의 주기는 T0, T1로 정의한다. 상태벡터와 측정치 yk로 디지털 위상 고정루프의 상태공간 모델을 나타내면 다음과 같다.
| (1) |
여기서 은 상태공간을 이루는 시스템 행렬, wk, vk는 상태 공간 모델의 시스템 모델 잡음과 측정 모델의 잡음벡터로 가우시안 백색 잡음으로 정의되며, 평균이 0, 분산이 각각 Q와 R로 정의된다. 디지털 위상 고정루프의 루프 필터 설계시 식 (1)과 같이 제어입력이 없는 모델을 사용하는 경우가 많으며, 본 논문에서도 제어입력이 없는 상태공간 모델을 사용하였다[1]. 디지털 위상 고정루프설계를 위해 스택된 측정값 을 유한한 측정값 구간 [k-N, k-1]에서 N개의 측정값을 쌓으면 다음 과같이 표현된다.
| (2) |
여기서 각각의 행렬은 다음과 같이 표현된다.
식 (1)로부터 MN = [AN-1G AN-2 G ⋯ G]를 정의한 후 다음 수식을 얻을 수 있다.
| (3) |
유한 임펄스 응답 상태추정기는 가장 최근의 측정값 N개 사용하며 다음과 같이 표현된다.
| (4) |
여기서 H는 이득행렬이며 식 (4)에 식 (2)를 대입한 후 식 (3)을 더하면 다음과 같이 표현된다.
| (5) |
여기서 식 (5)의 양변에 기대값을 취한 후 불편성조건 을 만족하면 상태벡터와 상태벡터의 추정값이 같아진다. 이득행렬을 구하기 위해 다음과 같은 비용함수 J를 정의한다.
| (6) |
여기서 ∥•∥F는 프로베니우스 놈을 의미하며, 는 0과 1사이의 값을 갖는 행렬 이득 가중치 파라미터이다. 식 (6)은 라그랑주 승수법을 사용하면 다음과 같다.
| (7) |
여기서 Γ는 라그랑주 연산자를 의미하며, 식 (7)를 최소화하기 위해 이득 H로 편미분을 취하면 다음과 같이 표현된다[9].
| (8) |
식 (8)을 활용하여 이득을 구하면 다음과 같다.
| (9) |
제안된 디지털 위상고정 루프의 성능을 향상시키기 위해서 최적의 측정값 구간의 길이(Optimal horizon size)와 최적의 행렬 이득 가중치 파라미터 가 필요하다. 두 가지 파라미터 최적화를 해석적 방법으로 구하기 어려워서 수치적인 방법을 통해 얻는다. 측정값 구간의 길이와 행렬 이득 가중치 파라미터 최적화 결정 순서에 관한 연구는 아직 밝혀지지 않은 좋은 연구 주제이며, 본 논문에서는 최적의 행렬 이득 가중치 파라미터를 먼저 구하고 이후 최적의 측정값 구간의 길이를 구한다. 설계한 새로운 디지털 위상 고정루프의 두 가지 파라미터 최적화 방법은 3.1절에서 서술한다.
Ⅲ. 시뮬레이션 결과
3.1 파라미터 최적화
이번 절에서는 설계한 디지털 위상 고정루프의 설계 파라미터 측정값 구간의 길이와 행렬 이득 가중치 파라미터Ω 최적화에 관하여 서술한다. 먼저 시뮬레이션을 수행하기 위한 수신기와 발신기의 타이밍 오프셋을 각각 T0 = 0.0001, T1 = 1.1 T0로 설정, 잡음 공분산을 로 설정하였다[1]. 시뮬레이션의 파라미터 값은 이상적인 상황에서의 환경을 가정하였으며, 송신기와 수신기의 타이밍 오프셋 등 여러 환경이 바뀔 수 있어 이상적인 상황을 가정하여 파라미터를 수치적 방법으로 최적화하였다.
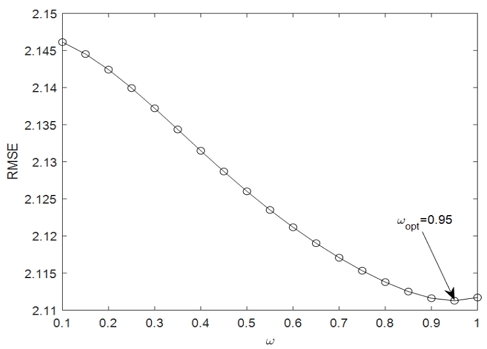
그림 2에서는 행렬 이득 가중치 파라미터 값을 0.1에서부터 1까지 변경해가며 평균 제곱근 오차(RMSE, Root Mean Square Error)를 비교하였다. 여기서 horizon size는 4로 설정하고 시뮬레이션을 수행하였다. 평균 제곱근 오차를 분석해 본 결과 행렬 이득 가중치 파라미터가 0.95일 때 최적의 값이 나오는 것을 확인할 수 있었으며, 시뮬레이션에서 제안한 디지털 위상 고정 필터를 설계할 때 행렬이득 가중치 파라미터를 ω = 0.95로 설계하였다.
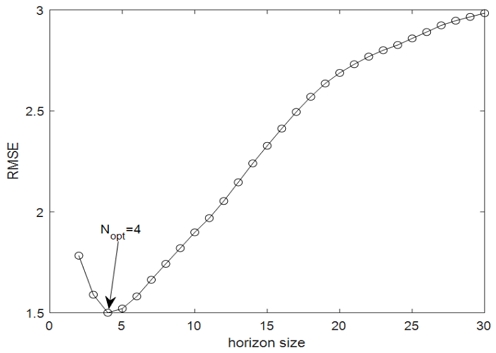
최적의 측정값 구간의 길이를 취득하기 위해 horizon size를 2부터 30까지 변경하였다. horizon size는 시스템 행렬 A의 크기인 2보다 반드시 같거나 커야 한다는 조건이 존재하기 때문에 최소값을 2로 설정하였다. 그림 3의 결과를 보았을 때 최적의 horizon size를 평균 제곱근 오차 RMSE값이 제일 낮은 4로 결정하였으며, 실제 시뮬레이션에서 새로운 디지털 위상 고정필터를 설계할 때 최적의 측정값 구간의 길이를 N=4로 설계하였다.
3.2 성능 평가
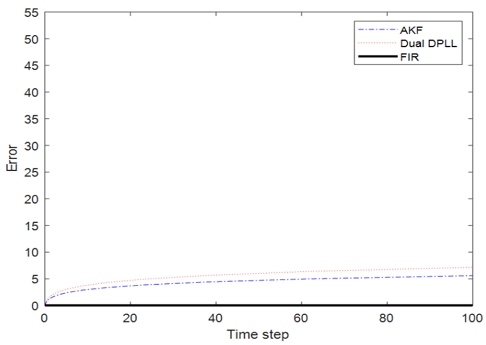
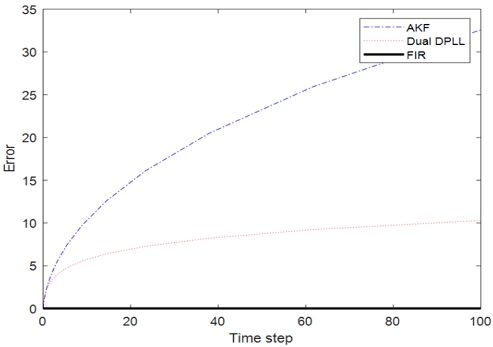
이번 절에서는 적응형 칼만 필터 기반의 디지털 위상 고정루프, 듀얼 루프 디지털 위상 고정루프, 그리고 유한 임펄스 응답 필터 기반의 디지털 위상 고정루프의 성능을 비교해 보았다. 그림 4는 이상적인 상황에서 세가지 디지털 위상 고정루프의 성능 평가를 수행, 그림 5은 필터 설계를 위한 초기값 , 필터 설계를 위한 잡음 공분산 Qfilter = 0.25Q, Rfilter = 4R로 설정하여 부정확한 상황에서의 세가지 디지털 위상 고정루프의 성능을 나타내며, 표 1은 이상적인 상황과 부정확한 상황에서의 세 가지 필터 기반 디지털 위상 고정루프의 RMSE를 나타낸다. 그림에서의 오차(Error) 값은 실제값과 추정값의 차이의 절대값으로 정의하였다. 이상적인 상황에서는 세 가지 디지털 위상 고정루프의 성능이 모두 우수한 것을 확인하였다. 하지만, 초기값과 잡음 공분산이 부정확한 상황에서는 무한 기억 상태추정기의 오차가 누적되는 현상으로 인해 적응형 칼만필터 기반의 디지털 위상 고정루프의 성능이 낮은 것을 확인할 수 있었다. 듀얼 루프 기반의 디지털 위상 고정루프는 비교적 낮은 오차 값을 갖지만, 제안한 디지털 위상 고정루프의 경우 유한기억 상태 추정기의 특징으로 인한 오차 누적현상이 없기 때문에 초기값과 잡음 공분산이 부정확한 상황에 가장 강인한 성능을 갖는다.
Ⅳ. 결론 및 향후 과제
본 논문에서는 최적의 측정값 구간 길이와 최적의 행렬 이득 가중치 파라미터값을 갖는 프로베니우스 놈 유한 임펄스 응답 상태추정기 기반 디지털 위상 고정루프 설계 방법에 대해 서술하였다.
제안된 새로운 디지털 위상 고정루프의 이득값은 라그랑주 승수법을 통하여 최적의 이득값을 구하였고, 수치적으로 최적의 파라미터 설계하는 방법에 대하여 서술하였다. 이상적인 상황에서는 기존의 디지털 위상 고정루프와 제안한 방법의 성능이 큰 차이가 없으나, 초기값, 오차 공분산 값이 부정확한 상황에서 제안된 디지털 위상 고정루프가 기존의 방법들 보다 강인한 성능을 갖는 것을 시뮬레이션 결과를 통하여 입증하였다. 본 논문에서 서술한 상태추정기의 확장으로 향후 드론의 위치 추정, 미사일의 추적 등 통신, 제어, 항공분야 등 다양한 분야에서 적용될 것으로 예상된다.
Acknowledgments
이 논문은 2020년도 조선대학교 연구비의 지원을 받아 연구되었음
References
-
P. Driessen, "DPLL bit synchronizer with rapid acquisition using adaptive Kalman filtering techniques", IEEE Transactions on Communications, Vol. 42, No. 9, pp. 2673-2675, Sep. 1994.
[https://doi.org/10.1109/26.317406]

-
A. Patapoutian, "On phase-locked loops and Kalman filters", IEEE Transactions on Communications, Vol. 47, No. 5, pp. 670-672, May 1999.
[https://doi.org/10.1109/26.768758]

-
B. Chun, Y. H. Lee, and B. Kim, "Design of variable loop gains of dual-loop DPLL", IEEE Transactions on Communications, Vol. 45, No. 12, pp. 1520-1522, Dec. 1997.
[https://doi.org/10.1109/26.650226]

-
N. Y. Ko and T. G. Kim, "Comparison of Kalman filter and particle filter used for localization of an underwater vehicle", 2012 9th international conference on ubiquitous robots and ambient intelligence(URAI), Daejeon, Korea, Nov. 2012.
[https://doi.org/10.1109/URAI.2012.6463013]

-
W. Muhammad and A. Ahsan, "Airship aerodynamic model estimation using unscented Kalman filter", Journal of Systems Engineering and Electronics, Vol. 31, No. 6, pp. 1318-1329, Dec. 2020.
[https://doi.org/10.23919/JSEE.2020.000102]

-
H. G. Marina, et al., "UAV attitude estimation using unscented Kalman filter and TRIAD", IEEE Transactions on Industrial Electronics, Vol. 59, No. 11, pp. 4465-4474, Nov. 2012.
[https://doi.org/10.1109/TIE.2011.2163913]

-
C. Luo, et al., "UAV position estimation and collision avoidance using the extended Kalman filter", IEEE Transactions on vehicular technology, Vol. 62, No. 6, pp. 2749-2762, Jul. 2013.
[https://doi.org/10.1109/TVT.2013.2243480]

-
C. K. Ahn, "l2 - l∞Elimination of Overflow Oscillations in 2-D Digital Filters Described by Roesser Model With External Interference", IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 60, No. 6, pp. 361-365, Jun. 2013.
[https://doi.org/10.1109/TCSII.2013.2258259]

-
S. H. You, C. K. Ahn, Y. S. Shmaliy, and S. Zhao, "Fusion Kalman and weighted UFIR state estimator with improved accuracy", IEEE Transactions on Industrial Electronics, Vol. 67, No. 12, pp. 10713-10722, Dec. 2020.
[https://doi.org/10.1109/TIE.2019.2958278]

-
S. H. You, J. M. Pak, C. K. Ahn, P. Shi, and M. T. Lim, "Unbiased finite-memory digital phase-locked loop", IEEE Transactions on Circuits and Systems II: Express Briefs, Vol. 63, No. 8, pp. 798-802, Aug. 2016.
[https://doi.org/10.1109/TCSII.2016.2531138]

-
S. Zhao, Y. S. Shmaliy, and F. Liu, "Fast computation of discrete optimal FIR estimates in white Gaussian noise", IEEE Signal Processing Letters, Vol. 22, No. 6, pp. 718-722, Jun. 2015.
[https://doi.org/10.1109/LSP.2014.2368777]

-
J. Fu, J. Sun, S. Lu, and Y. Zhang, "Maneuvering target tracking with modified unbiased FIR filter", Journal of Beijing University of Aeronautics and Astronautics, Vol. 41, No. 1, pp. 77–82, Jan. 2015.
[https://doi.org/10.13700/j.bh.1001-5965.2014.0068]

-
C. K. Ahn and Y. S. Shmaliy, "New receding horizon FIR estimator for blind smart sensing of velocity via position measurements", IEEE Trans. Circuits Syst. II, Vol. 65, No. 1, pp. 135-139, Jan. 2018.
[https://doi.org/10.1109/TCSII.2017.2707123]

-
Y. S. Shmaliy, "An iterative Kalman-like algorithm ignoring noise and initial conditions", IEEE Trans. Signal Process., Vol. 59, No. 6, pp. 2465-2473, Jun. 2011.
[https://doi.org/10.1109/TSP.2011.2129516]


2013년 2월 : 서울과학기술대학교 전자 IT미디어공학부(공학사)
2019년 2월 : 고려대학교 전기전자공학부 대학원(공학박사)
2019년 3월 ~ 2020년 2월 : 고려대학교 연구교수
2020년 ~ 현재 : 조선대학교 전자공학부 조교수
관심분야 : 상태추정기, 측위 및 위치추정 알고리즘, 지능제어, 최적제어, 드론, 자율주행

2013년 2월 : 고려대학교 전기전자공학부(공학사)
2019년 8월 : 고려대학교 전기전자공학부 대학원(공학박사)
2019년 9월 ~ 2020년 2월 : 고려대학교 연구교수
2020년 3월 ~ 2020년 8월 : LG전자 선임연구원
2020년 8월 ~ 현재 : 상명대학교 소프트웨어학과 조교수
관심분야 : 컴퓨터 비전, 임베디드, 지능형 데이터 시스템, 자율주행

2011년 2월 : 고려대학교 전기전자공학부(공학사)
2017년 2월 : 고려대학교 전기전자공학부 대학원(공학박사)
2017년 3월 ~ 2018년 9월 : 현대모비스 전자현가설계팀 책임연구원
2018년 9월 ~ 2019년 8월 : 삼성전자 무선사업부 AI개발 그룹 책임연구원
2019년 9월 ~ 현재 : 전남대학교 ICT융합시스템공학과 조교수
관심분야 : 지능제어 및 응용, 인공지능, 자율주행, 드론지능제어, 최적