콘볼루션 신경망의 학습 성능 강화를 위한 그레디언트의 복합적 분석 및 활용 방법

Ⅰ. 서 론

1998년에 처음 소개된 콘볼루션 신경망(CNN, Convolutional Neural Networks)[1]은 이미지 처리에서 널리 활용되는 콘볼루션 연산을 포함한 다양한 연산을 활용하여 주어진 데이터로부터 특징(Feature) 정보를 정확하게 추출하는 기능을 갖고 있다[2].

이러한 특성에 기반하여, 콘볼루션 신경망은 이미지 분류와 세그먼테이션, 객체 탐지 및 추적과 같은 컴퓨터 비전 분야를 비롯하여 자연어처리, 시계열 분석 등 다양한 영역에서 널리 활용되고 있다[2]-[6].

최근의 콘볼루션 신경망은 이미지 또는 텍스트와 같이 복잡한 데이터의 인식 성능을 강화하기 위해 그 구조가 점점 복잡해지고 있다. 대표적으로 2015년에 발표된 ResNet[7]의 경우 입력 계층의 증가에 따른 데이터 전달 시 손실 문제를 해결하기 위해 잔차 연결(Residual connection)을 도입하였으며, 2017년에 소개된 DenseNet[8]은 각각의 계층의 입/출력을 다른 계층과 직접적으로 연결하는 여러 개의 댄스 블록(Dense block)으로 구성된다.

이처럼 콘볼루션 신경망의 구조가 복잡해짐에 따라 그것의 손실함수(Loss function)가 생성하는 해 공간(Optimal solution space)의 복잡도 역시 높아지게 되어 전역 최적 해(Optimal solution), 즉, 콘볼루션 신경망의 최적 가중치(Optimal weights)를 탐색하는 것을 더욱 어렵게 한다. 이는 결과적으로 콘볼루션 신경망의 학습 성능 저하로 이어지게 된다.

한편 콘볼루션 신경망을 포함한 심층 신경망 학습은 대부분 경사 하강법(Gradient descent)을 기반으로 한 일차 최적화 알고리즘(First-order optimization algorithm)을 통해서 이루어진다[9].

특히 현재 단계(Step)에서 관측되는 그레디언트(Gradient)와 과거의 여러 그레디언트들의 지수 가중 평균(Exponential weighted average)을 참조하여 최적 해의 탐색 방향을 적응적으로 결정하는 학습 알고리즘인 Adam[10]이 다양한 심층 신경망의 학습에 널리 사용되고 있다.

그러나 상기에서 설명한 바와 같이 최근 콘볼루션 신경망의 구조가 더욱 방대해지고 복잡해짐에 따라 Adam에서 제안한 방법만으로 콘볼루션 신경망을 학습시키는 경우 만족할 만한 수준의 학습 성능에 도달하지 못하는 문제점이 발생하게 되었다. 이에 따라 Adam에서 제안한 방법보다 더욱 정교하면서도 안정적으로 콘볼루션 신경망을 학습시킬 수 있는 강화된 최적 해 탐색 알고리즘에 대한 필요성이 대두되기 시작하였다.

따라서, 본 논문에서는 콘볼루션 신경망 학습 시 손실함수가 생성하는 전역 최적 해 공간에서 효과적으로 해 탐색을 수행하기 위한 그레디언트의 복합적 분석 및 활용 방법을 제안한다. 그런 다음, 제안한 방법을 활용한 새로운 콘볼루션 신경망 학습 방법인 CGAU-CNN(Complex Gradient Analysis and Utilization for CNN) 학습 알고리즘을 소개하고 그것의 구체적인 구현 방법을 보인다. 마지막으로, CGAU-CNN을 이용하여 실제 널리 사용되는 콘볼루션 신경망 모델을 학습시키고 그 결과를 분석함으로써 본 연구에서 제안하는 방법의 성능과 효용성을 입증한다.

본 논문의 구성은 다음과 같다. II 장에서는 콘볼루션 신경망과 학습 방법에 관한 기존 연구를 소개한다. III 장에서는 그레디언트의 복합적인 분석 방법과 이를 활용한 강화된 콘볼루션 신경망 학습 알고리즘인 CGAU-CNN을 제안한다. IV 장에서는 본 연구에서 제안한 CGAU-CNN과 5개의 기존 학습 알고리즘을 이용하여 실제 콘볼루션 신경망 모델을 학습시킨 후 학습된 신경망 모델의 정확도와 수렴 성능을 분석한다. 마지막으로 V 장에서는 본 논문의 내용을 요약하고 제안하는 방법의 의의와 한계점 및 향후 연구 방향을 설명하면서 본 논문을 마무리한다.

Ⅱ. 관련 연구

콘볼루션 신경망은 1979년 쿠니히코 후쿠시마(Kunihiko Fukushima)가 개발한 네오코그니트론(Neocognitron)[11]의 영향을 받아 1998년에 얀 르쿤(Yann LeCun)이 제안한 신경망 모델이다[1][12].

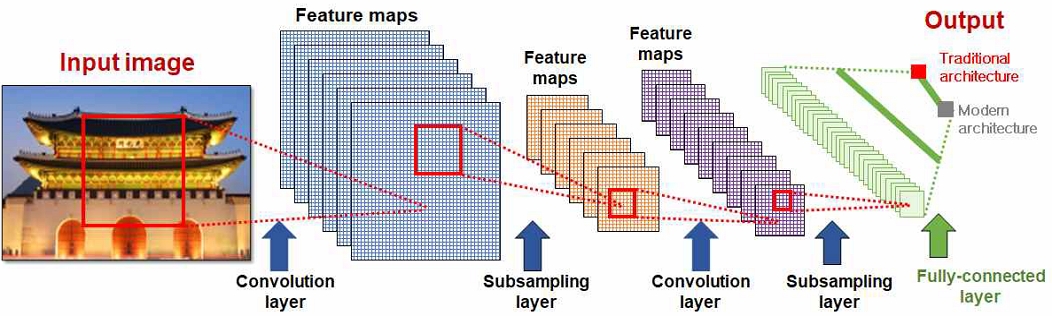
그림 1은 콘볼루션 신경망의 일반적인 구조를 보여주고 있다.

Fig. 1.

General architecture of convolutional neural networks

콘볼루션 신경망에서의 학습 문제는 이미지 분류 또는 이미지 세그먼테이션과 같은 작업을 주어진 학습 데이터에 대해서 최적의 성능으로 수행할 수 있도록 콘볼루션 계층(Convolution layer) 상의 콘볼루션 필터(Convolution filter)와 그 외 여러 가중치에 대한 최적의 값을 탐색하는 최적화 문제(Optimization problem)로 정의할 수 있다. 이에 따라 얀 르쿤은 자신이 개발한 콘볼루션 신경망인 LeNet-5를 학습시키기 위해 오차 역전파(Backpropagation) 알고리즘을 활용하여 번호판 이미지를 정확하게 인식하는 데 성공하였다[1]. 오차 역전파 알고리즘은 콘볼루션 신경을 포함한 대부분의 신경망을 학습시키는 방법으로 널리 활용되고 있다.

오차 역전파 알고리즘의 핵심은 손실함수의 그레디언트를 활용하는 것으로써 가장 대표적인 방법으로 경사 하강법(Gradient descent)이 있다. 경사 하강법은 최적 해 공간 내에서 각 단계별로 관측되는 그레디언트가 가리키는 방향을 참조하여 점진적으로 최적 해를 탐색해 나가는 방법으로, 구현이 간단하고 계산량이 비교적 적다는 장점이 있으나 국소 또는 전역 최적 해 주변에서 탐색 경로가 심하게 진동하는 문제점을 갖고 있다. 이는 궁극적으로 최적 해 탐색의 속도를 느려지게 할 뿐만 아니라 자칫 국소 최적 해에 수렴함에 따라 전역 최적 해를 발견하지 못하는 현상을 야기할 수 있다.

이러한 문제점을 해결하기 위해서 해 탐색의 방향과 속도를 적응적으로 제어하여 최적 해의 품질과 수렴 성능을 향상시키기 위한 여러 방법이 제안되었다. 대표적으로 2014년에 발표된 Adam 알고리즘은 과거 관측된 그레디언트들의 지수 가중 평균인 모멘텀(Momentum)을 활용하여 탐색의 방향을 결정함과 동시에 탐색 강도(Strength)를 적응적으로 조절하는 방법을 도입하였으며, 그 결과 기존의 경사 하강법보다 더욱 빠른 수렴 속도와 높은 학습 정확도를 달성하였다. 이에 따라 오늘날 심층 신경망의 학습은 Adam 또는 그것을 기반으로 하여 개발된 “Adam 계열 학습 알고리즘”을 활용하여 수행하는 것이 일반적이다[9]. 최근 개발된 대표적인 Adam 계열 학습 알고리즘으로 AdaBelief[13]와 diffGrad[14], AngularGrad[15] 등이 있다.

그럼에도 불구하고, 이러한 기존의 Adam 계열의 학습 알고리즘들은 콘볼루션 신경망의 구조가 점점 더 복잡해지고 그 규모 또한 방대해짐에 따라 그것의 손실함수가 구성하는 대규모 최적 해 공간에서 효과적으로 전역 최적 해를 탐색하는 데 많은 어려움을 겪는다. 이에 본 논문에서는 Adam 계열 학습 알고리즘을 활용하여 전역 최적 해 탐색 시 발생하는 문제점들을 효과적으로 해결하기 위해 그레디언트 정보를 어떻게 복합적으로 활용할 수 있는가에 관하여 심층적으로 다루고자 한다.

Ⅲ. 그레디언트의 복합적 분석과 이를 활용한 콘볼루션 신경망 학습 알고리즘

앞서 II 장에서 설명한 바와 같이 현대의 콘볼루션 신경망은 각 계층별로 콘볼루션 필터와 서브 샘플링 연산을 포함하고 이에 더해 잔차 연결 및 댄스 블록과 같은 구조가 결합된 상당히 높은 복잡도를 갖는다. 이 경우, 콘볼루션 신경망의 손실함수가 생성(Span)하는 대규모의 가중치 해 공간(Weight solution space)의 형태(Surface)가 복잡해짐에 따라 손실함수를 최소화하는 전역 최적 해(즉, 최적 가중치 Optimal weights)를 탐색하는 데 많은 어려움이 발생한다. 특히, 심층 신경망 학습에 널리 사용되는 경사 하강법의 경우 각 단계별로 그레디언트가 가리키는 방향에 의존하여 최적 해 탐색을 수행한다. 이는 곧 그레디언트를 어떻게 활용하는가에 따라 최적 해의 품질과 학습된 모델의 성능에 중요한 영향을 미칠 수 있음을 의미한다. 실제로, 콘볼루션 신경망의 학습 과정에서 그레디언트를 다양한 방법으로 분석하고 활용함으로써 학습된 모델의 성능을 유의미하게 향상시킬 수 있음을 본 논문의 선행 연구인 “HyAdamC: A New Adam-Based Hybrid Optimization Algorithm for Convolution Neural Networks[16]”를 통해서 확인한 바 있다.

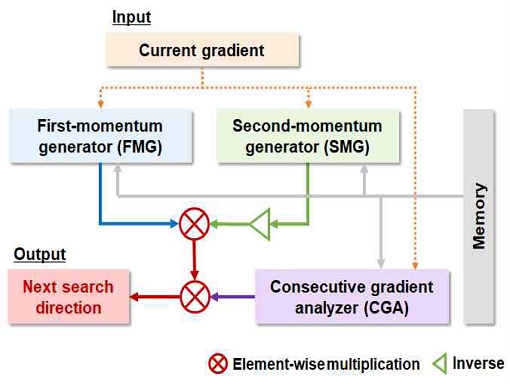
이에 따라, 본 논문에서는 최적 해 탐색 시 각 단계에서 측정되는 손실함수의 그레디언트를 다양한 방법으로 분석하여 최적 해 탐색에 복합적으로 활용하는 방법을 소개하고, 이를 결합한 새로운 Adam 계열의 학습 알고리즘인 CGAU-CNN을 제안한다. 그림 2는 CGAU-CNN에서 최적 해 탐색 방향과 강도를 결정하는 방법을 설명한 다이어그램이다. 현재 단계 t에서 그레디언트 g_t가 관찰될 때 CGAU-CNN은 세 가지의 그레디언트 분석 메커니즘을 복합적으로 활용하여 다음 단계 t+1에서의 해 탐색 방향을 결정한다. 그림 2에 표현된 세 가지의 그레디언트 분석 메커니즘을 구체적으로 설명하면 다음과 같다.

Fig. 2.

Gradient analysis mechanisms of CGAU-CNN

3.1 그레디언트의 복합적 분석 방법

3.1.1 FMG(First-Momentum Generator)

그레디언트는 매 단계에서 최적 해 탐색 방향을 결정하는 가장 중요한 요소로서 해 품질에 중요한 영향을 미친다. 그러나 각 단계에서 발견되는 그레디언트가 항상 최적 해 방향을 가리키지는 않으므로 과거 그레디언트들의 지수 가중 평균인 일차 모멘텀(First-momentum)을 참조하여 해 탐색 방향을 결정하는 것이 일반적인 방법이다. 그러나 일부 단계에서 관측되는 그레디언트가 기존의 탐색 방향과 크게 어긋나는 경우 이를 일차 모멘텀에 그대로 반영하면 일차 모멘텀이 가리키는 최적 해 탐색 방향이 계속해서 왜곡되는 문제점이 있다[16]. 결과적으로 해 탐색의 정확도를 향상시키기 위해서는 일차 모멘텀 계산 시 이와 같은 아웃라이어(Outlier) 경향을 보이는 그레디언트의 반영 비율을 감소시켜야 한다. 이러한 그레디언트를 본 논문에서는 아웃라이어 그레디언트(Outlier gradient)[17]라 정의한다.

이를 위해 FMG에서는 먼저 현재의 그레디언트와 과거에 탐지된 일차 모멘텀 사이의 차이를 계산하고, 이에 기반하여 현재 그레디언트와 이전 그레디언트들의 탐색 경향 간의 상이한 정도를 측정한다. 이는 아래의 식 (1)과 같이 계산할 수 있다[16].

$\[ q_{t+1}=2n{\left(n+\sum _{j=1}^n\frac{{\left(g_{t,j}-m_{t,j}\right)}^2}{v_{t,j}+ϵ}\right)}^{-1} \]$

(1)

위의 식 (1)에서 n은 차원의 수(Dimension)를 나타내며, v_t는 그레디언트 g_t의 각 요소(Element)에 대한 분산(Variance)을 나타낸다. 식 (1)을 분석하면 기존의 일차 모멘텀 m_t와 현재 관측된 그레디언트 g_t가 상이할수록 q_t+1의 크기가 감소하게 된다. 이를 일차 모멘텀 계산 시 계수(Coefficient value)로 활용하면, q_t+1의 값이 작아질수록 해당 그레디언트의 반영률을 감소시킴으로써 해 탐색 방향이 급격하게 변화하는 것을 예방할 수 있다. 이를 수식으로 표현하면 다음과 같다.

$\[ m_{t+1}={\left(Q_t+q_{t+1}\right)}^{-1}\left(Q_t{m}_t+q_{t+1}{g}_t\right) \]$

(2)

이때, 식 (2)에서 사용되는 Q_t는 q₁부터 q_t까지의 지수 가중 평균으로 q_t+1의 갑작스러운 변화에도 불구하고 일차 모멘텀 계산 시 계수가 안정적으로 변화할 수 있도록 아래와 같이 계산된다.

$\[ Q_{t+1}=\left(2-{\beta }_1^{-1}\right)Q_t+q_{t+1} \]$

(3)

FMG에서 일차 모멘텀을 계산하는 원리를 정리하면 다음과 같다. 일차 모멘텀 m_t+1 계산 시 그레디언트 g_t와 이전의 일차 모멘텀 m_t 간의 상이함의 정도가 클수록 식 (2)에서 그레디언트 g_t의 계수인 q_t+1/(Q_t+q_t+1)가 작아지게 된다. 반면에, m_t의 계수인 Q_t/(Q_t+q₊₁)는 상대적으로 더욱 커지게 되어 결과적으로 m_t+1을 계산할 때 그레디언트 g_t의 반영률이 감소하고 기존의 모멘텀 m_t의 반영률이 더욱 강화된다. 이는 곧 현재 단계에서 관측된 그레디언트가 아웃라이어의 경향을 보이면 그 정도에 따라 일차 모멘텀 계산 시 그것의 반영률이 감소하게 됨을 의미한다.

이후 CGAU-CNN은 FMG에서 계산된 일차 모멘텀 m_t+1이 가리키는 방향을 참조하여 최적 해 탐색을 진행한다. 이에 대한 구체적인 구현 방법은 3.2장에서 자세히 설명한다.

3.1.2 SMG(Second-momentum Generator)

FMG에서 생성된 일차 모멘텀 m_t+1이 해 탐색의 방향(Direction)을 결정한다면, 이차 모멘텀(Second-momentum)은 각 차원별로 탐색의 강도를 적응적으로 제어한다. 기존의 Adam에서는 그레디언트의 각 요소를 제곱한 결과에 대한 지수 가중 평균을 구함으로써 이차 모멘텀을 계산한다. 그러나 이와 같은 방법은 그레디언트 각 요소의 크기에 따라 탐색 강도가 과도하게 영향을 받는 문제점이 있으며, 이는 최적 해 탐색 성능을 저하시키는 원인이 된다. 이러한 문제점을 보완하기 위해서 본 연구에서는 현재 시점 t에서 관측된 그레디언트 g_t와 식 (2)에서 계산된 g_t가 반영된 일차 모멘텀 m_t+1을 사용하여 이차 모멘텀을 계산한다[13]. 이를 식으로 나타내면 다음과 같다.

$\[ s_{t+1}={\beta }_2{s}_t+\left(1-{\beta }_2\right){\left(m_{t+1}-g_t\right)}^2 \]$

(4)

한편, 식 (4)에서 이차 모멘텀 계산 시 탐색 단계 t에 따라 점진적으로 이차 모멘텀의 영향력을 강화할 수 있다. 이는 해 탐색 과정 초기에는 탐색의 다양성을 유지하되 탐색이 진행될수록 그레디언트를 집중적으로 활용하는 것이 최적 해 탐색에 유용하기 때문이다. 이를 식으로 표현하면 다음과 같다.

$\[ s_{t+1}^{\text{*}}=s_{t+1}+\frac{\delta }{t} \]$

(5)

상기 식 (5)에서 δ/t는 탐색이 진행됨에 따라 0으로 수렴하게 된다. 즉, $$ \underset{t\to \infty }{\text{lim}}{s}_{t+1}^{\mathrm{*}}=s_{t+1}$$이기 때문에 해 탐색이 진행될수록 해 탐색의 강도를 조절하는 과정에서 δ/t의 영향은 줄어듦과 동시에 이차 모멘텀 s_t+1이 점진적으로 완전하게 반영된다. 이렇게 계산된 이차 모멘텀 $$ s_{t+1}^{\mathrm{*}}$$은 식 (2)에서 계산된 일차 모멘텀 m_t+1에 각 요소별로 곱해짐으로써 일차 모멘텀 각 차원의 탐색 강도를 적응적으로 조절하게 된다.

3.1.3 CGA(Consecutive Gradients Analyzer)

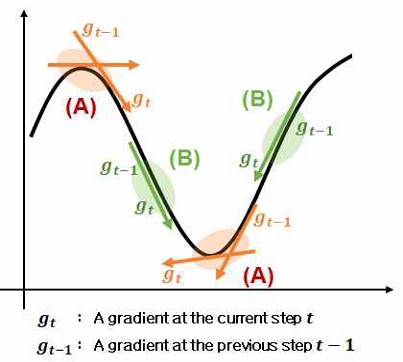
SMG와는 달리 CGA 메커니즘은 바로 직전 단계에서 관측된 그레디언트 g_t-1에서 현재 그레디언트 g_t로의 변화 정도에 따라 탐색 강도를 적응적으로 조절하는 방법이다[16]. 그림 3은 CGA에서 두 그레디언트 g_t-1과 g_t를 이용하여 탐색 강도를 조절하는 간단한 예시를 보여주고 있다. 그림 3에서 구간 (A)는 그레디언트가 급격하게 변화하는 경우를 나타낸 것이다. 이는 주변에 전역 또는 국소 최적 해가 위치할 때 주로 발생하며, 이러한 상황에서는 탐색 강도를 낮추어 해 탐색 시 자칫 해당 최적 해를 지나치지 않도록 세밀하게 탐색을 제어해야 한다.

Fig. 3.

Control mechanism of CGA in CGAU-CNN

반면에 (B)는 그레디언트가 일정하게 유지되는 구간을 표현한 것으로, 이는 주변에 최소점이 존재하지 않음을 의미한다. 따라서 이 경우에는 현재의 탐색 강도를 계속 유지하거나 더욱 강화하여 수렴을 촉진하는 것이 바람직하다[14]. 아래의 식 (6)은 현재 및 직전에 관측된 두 그레디언트 g_t와 g_t-1의 변화 정도에 따라 탐색 속도를 제어하는 방법을 수학적으로 모델링한 것이다.

$\[ {\psi }_{t+1}=\frac{1}{1+e^{-\left|g_t-g_{t-1}\right|}} \]$

(6)

상기 식 (6)을 통해 계산된 Ψ_t+1은 각 요소별로 0.5에서 1 사이의 값을 갖는다. 결과적으로 Ψ_t+1은 전역 최적 해 탐색 시, 두 그레디언트 사이의 변화 정도에 따라 각 차원의 탐색 강도를 최대 절반으로 감소시킬 수 있는 계수로써 활용될 수 있다[14][16]. 이는 Ψ_t+1을 일차 모멘텀 m_t+1에 각 요소별로 곱하는 연산(Element-wise multiplication)을 통해 구현될 수 있다.

3.2 그레디언트의 복합적 분석에 기반한 콘볼루션 신경망 학습 알고리즘

앞서 설명한 세 가지 그레디언트 분석 메커니즘을 결합하여 콘볼루션 신경망의 학습 성능을 강화하기 위한 새로운 Adam 계열 학습 알고리즘인 CGAU-CNN을 아래의 표 1과 같이 구현할 수 있다. 이때 두 그레디언트 간의 요소별로 곱셈을 수행하는 연산은 “•”로 표기하였다. CGAU-CNN에서 콘볼루션 신경망 모델을 학습시키는 전체적인 과정은 기존의 Adam과 유사하다. 다만, 표 1에서 3~5번째 줄은 FMG, 6~7번째 줄은 SMG, 9번째 줄은 CGA 메커니즘에 각각 대응되며, 10번째 줄의 코드와 같이 이들을 복합적으로 활용하여 탐색 방향과 강도를 적응적으로 조절하는 것이 Adam과 가장 큰 차이점이라 할 수 있다. 표 1에서 설명한 CGAU-CNN의 실제 성능 평가 결과는 이어지는 IV 장에서 자세히 다루어진다.

Table 1.

Pseudocode of CGAU-CNN optimizer

Ⅳ. 실 험

4.2 실험 결과

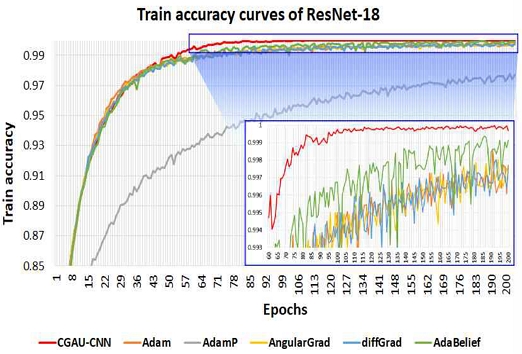
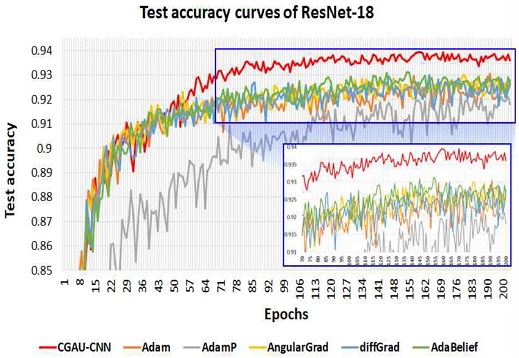
그림 4는 CGAU-CNN을 포함한 6가지 Adam 계열 학습 알고리즘을 활용하여 ResNet-18 모델을 학습시킬 때 각 Epoch에서 측정된 ResNet-18 모델의 훈련 정확도를 곡선으로 표현한 그래프(Curve plot)이다. 그림 4의 결과와 같이 본 논문에서 제안한 CGAU-CNN으로 ResNet-18을 학습시킬 때, 매우 안정적이면서도 빠른 수렴 속도로 학습을 진행할 수 있음을 확인할 수 있었다. 특히 기존 Adam 계열 학습 알고리즘 중에서 가장 빠른 수렴 속도를 갖는 것으로 확인된 AdaBelief의 훈련 정확도 곡선과 비교했을 때도, CGAU-CNN이 더욱 빠른 속도로 수렴함을 확인할 수 있었다. 이와 더불어, AdaBelief 이외의 다른 학습 알고리즘의 훈련 정확도 곡선과 비교했을 때도 CGAU-CNN의 수렴 성능이 정확도와 속도 측면에서 모두 우수함을 확인할 수 있다.

Fig. 4.

Train accuracy curves of ResNet-18 models trained by each of six optimizers

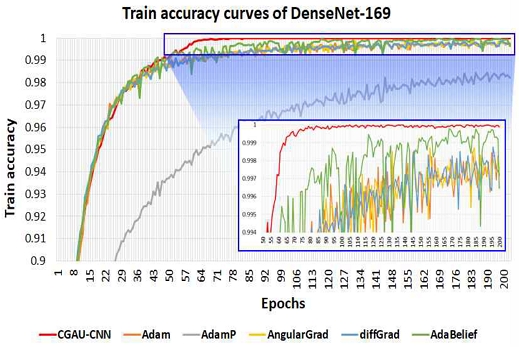
한편, DenseNet-169를 학습시켰을 때, 각 Epoch에서 측정된 훈련 정확도 곡선 그래프가 그림 5에 표현되어 있다. 그림 4의 ResNet-18 모델에 대한 훈련 정확도 곡선과 비교했을 때, DenseNet-169 모델을 학습시킬 때의 CGAU-CNN 수렴 성능이 다른 학습 알고리즘보다 더욱 좋은 것을 확인할 수 있다. 그뿐만 아니라, AdaBelief와 같은 일부 학습 알고리즘에서 측정된 훈련 정확도 곡선과 비교했을 때, CGAU-CNN에서 측정된 훈련 정확도 곡선의 경우 Epoch가 증가함에 따라 더욱 안정적으로 훈련 정확도가 향상됨을 확인할 수 있다. 이는 CGAU-CNN을 사용하여 콘볼루션 신경망 모델을 학습시킬 때 더욱 안정적으로 수렴할 수 있음을 의미한다. 특히 DenseNet-169 모델이 ResNet-18 모델보다 더욱 복잡한 구조를 갖는다는 점을 고려할 때, 이러한 실험 결과는 CGAU-CNN에서 사용하는 그레디언트의 복합적인 분석 방법이 다수의 콘볼루션 필터와 서브 샘플링 연산, 잔차 연결 및 댄스 블록 등이 복합적으로 결합된 콘볼루션 신경망에서 최적의 가중치 파라메터를 탐색하는 데 상당히 중요한 역할을 수행할 수 있음을 보여주는 것이라 할 수 있다.

Fig. 5.

Train accuracy curves of DenseNet-169 models trained by each of six optimizers

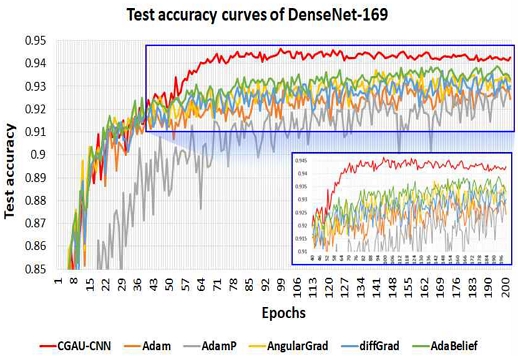
아울러, 앞서 4.1절에서 언급한 바와 같이 CGAU-CNN을 포함한 총 6개의 학습 알고리즘을 사용하여 학습된 ResNet-18과 DenseNet-169 모델 각각에 대한 테스트 정확도를 식 (8)을 이용하여 평가하고 그 결과를 비교하는 실험을 진행하였다. 그림 6과 7은 ResNet-18과 DenseNet-169 모델 학습 시 각 Epoch에서 측정된 테스트 정확도를 나타낸 곡선 그래프이다. 그림 6에서 CGAU-CNN의 테스트 정확도 곡선을 분석해보면, 약 50 Epoch을 수행한 이후의 테스트 정확도가 다른 학습 알고리즘의 테스트 정확도 곡선과 비교했을 때 눈에 띄게 증가함을 확인할 수 있다. 이와 유사하게 그림 7에 나타난 CGAU-CNN의 테스트 정확도 곡선 역시 다른 학습 알고리즘의 곡선과 비교했을 때 약 60 Epoch 이후 테스트 정확도가 더욱 향상됨을 확인할 수 있다.

Fig. 6.

Test accuracy curves of ResNet-18 models trained by each of six optimizers

Fig. 7.

Test accuracy curves of DenseNet-169 models trained by each of six optimizers

반면에 Adam, AngularGrad, diffGrad, AdaBelief와 같은 기존의 학습 알고리즘으로 학습 시 약 60 Epoch 이후부터는 CGAU-CNN으로 학습시킨 결과보다 낮은 테스트 정확도를 기록하였다. 이는 CGAU-CNN을 활용하여 ResNet-18과 DenseNet-169 모델을 학습시키면, 다른 Adam 계열 학습 알고리즘을 활용할 때보다 비교적 적은 Epoch만큼의 학습만으로도 정확도 측면에서 더욱 높은 수준의 학습 성능에 도달할 수 있음을 의미한다.

마지막으로, 총 200번의 Epoch 수행을 통해 학습된 ResNet-18과 DenseNet-169 모델의 최종 테스트 정확도 평가 결과가 표 2에 기술되어 있다. 본 논문에서 제안하는 학습 방법으로 ResNet-18 모델과 DenseNet-169 모델을 학습시켰을 때 CIFAR-10 테스트 데이터셋 내의 이미지들을 가장 높은 정확도인 93.61%와 94.27%로 각각 분류할 수 있음을 확인하였다. 반면에, 최근에 개발된 Adam 계열의 학습 알고리즘인 AdamP와, AngularGrad, diffGrad, AdaBelief의 경우에는 Adam보다는 유사하거나 더욱 우수한 결과를 달성하였으나 CGAU-CNN보다는 낮은 테스트 정확도를 보여주었다. 일례로, diffGrad를 이용하여 ResNet-18과 DenseNet-169를 학습시켰을 때, 이들의 테스트 정확도는 각각 92.79%와 93.02%로 평가되었으며, AdaBelief의 경우에는 각각 92.63%와 93.29%의 테스트 정확도를 달성한 것으로 확인되었다. 한편, Adam을 사용하여 ResNet-18과 DenseNet-169 모델을 학습시켰을 때 200 Epoch에서 측정된 테스트 정확도는 각각 92.59%와 92.43%로 ResNet-18에서의 결과가 조금 더 높은 것으로 확인되었다. 이는 Adam에 의해 충분한 Epoch만큼의 학습이 진행된 후에는 두 모델 모두 유사한 정확도 구간으로 수렴하기에 발생한 현상으로, 200 Epoch 주변의 다른 Epoch에서 측정된 테스트 정확도 결과들을 비교한 결과 대부분의 Epoch에서 DenseNet-169의 테스트 정확도가 더 높게 측정된 것을 확인할 수 있었다.

Table 2.

Final test accuracy results of ResNet-18 and DenseNet-169 evaluated at epoch 200

이러한 일련의 실험 결과를 통해서 본 논문에서 제안한 그레디언트의 복합적인 활용 방법이 실제 CNN 모델을 학습시킬 때, 그것의 학습 정확도와 수렴 성능을 강화하는 데 중요한 기여를 할 수 있음을 확인할 수 있다.

Ⅴ. 결 론

본 논문에서는 그레디언트의 복합적인 활용을 통해 콘볼루션 신경망의 학습 성능을 더욱 강화하는 새로운 학습 알고리즘인 CGAU-CNN을 제안하였다. CGAU-CNN은 그레디언트를 활용한 탐색 방향 결정 시 아웃라이어 그레디언트의 영향력을 최소화함과 동시에 현재의 그레디언트와 직전 단계에서 관측된 그레디언트 사이의 변화율에 따라 해 탐색 속도를 적응적으로 조정한다. 그뿐만 아니라, 과거에 관측된 그레디언트들의 평균 이동 방향과 현재 그레디언트를 활용하여 최적 해 탐색 속도를 적응적으로 제어한다. 이를 통해 Adam을 포함한 기존의 여러 Adam 계열 학습 알고리즘보다 더욱 정교하게 최적 해 탐색을 수행할 수 있다.

이를 구체적으로 입증하기 위해서 CGAU-CNN을 포함한 총 6개의 Adam 계열 학습 알고리즘을 이용하여 대표적인 콘볼루션 신경망인 ResNet-18과 DenseNet-169 모델을 학습시키고 학습된 두 모델을 활용하여 CIFAR-10 데이터셋의 이미지에 대한 분류 정확도를 평가하는 실험을 진행하였다.

실험 결과 기존의 Adam 및 Adam 계열 학습 알고리즘과 비교했을 때, CGAU-CNN으로 학습시킨 ResNet-18과 DenseNet-169 모델이 더욱 안정적인 수렴 성능을 보임과 동시에 높은 정확도로 CIFAR-10 데이터셋의 이미지를 분류할 수 있음을 확인하였다. 이는 곧 콘볼루션 신경망의 손실함수가 구성하는 대규모의 최적 해 공간에서 그레디언트의 복합적인 활용이 전역 최적 해 탐색의 성능을 향상시키는데 유의미하게 기여할 수 있음을 의미한다.

그럼에도 불구하고, 이미지 분류 응용에만 국한하여 CGAU-CNN의 성능 평가를 진행한 점은 본 연구의 한계점이라 할 수 있다. 이에 따라, 향후 연구에서는 이미지 세그먼테이션 및 객체 탐지와 같은 다양한 응용에 대해서도 성능 평가를 진행하여 최적 해 탐색에 영향을 주는 다양한 요인들을 도출하고 나아가 CGAU-CNN의 학습 성능을 더욱 고도화하기 위한 연구를 수행할 예정이다.

Acknowledgments

이 논문은 2018년도 정부(과학기술정보통신부) 및 2022년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2018R1A5A7059549, No.2022R1I1A3065378)

References

• Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner, "Gradient-based learning applied to document recognition", Proc. of the IEEE, Vol. 86, No. 11, pp. 2278-2324, Nov. 1998. [https://doi.org/10.1109/5.726791]
• Z. Li, F. Liu, W. Yang, S. Peng, and J. Zhou, "A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects", IEEE transactions on neural networks and learning systems, Vol. 33, No. 12, pp. 6999-7019, Dec. 2022. [https://doi.org/10.1109/TNNLS.2021.3084827]
• S. M. Lee, S. Y. Lee, and N. Kim, "Improved Pancreas Segmentation using Multiple Concatenated U-Net Model for Medical Image Systems", The Journal of Korean Institute of Information Technology, Vol. 20, No. 5, pp. 81-87, May 2022. [https://doi.org/10.14801/jkiit.2022.20.5.81]
• Y. B. Park and Y. J. Song, "A Method for Detecting Unexpected Situations from Highway Driving Images using Object Detection and Tracking", The Journal of Korean Institute of Information Technology, Vol. 20, No. 5, pp. 47-54, May 2022. [https://doi.org/10.14801/jkiit.2022.20.5.47]
• P. W. Park, "Text-CNN Based Intent Classification Method for Automatic Input of Intent Sentences in Chatbot", The Journal of Korean Institute of Information Technology, Vol. 18, No. 1, pp. 19-25, Jan. 2020. [https://doi.org/10.14801/jkiit.2020.18.1.19]
• B. W. Oh, "A Method of Spatial Data Classification using CNN", The Journal of Korean Institute of Information Technology, Vol. 20, No. 4, pp. 25-30, Apr. 2022. [https://doi.org/10.14801/jkiit.2022.20.4.25]
• K. He, X. Zhang, S. Ren, and J. Sun, "Deep Residual Learning for Image Recognition", Proc. of 2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, USA, pp. 770-778, Jun. 2016. [https://doi.org/10.1109/CVPR.2016.90]
• G. Huang, Z. Liu, L. Maaten, and K. Q. Weinberger, "Densely Connected Convolutional Networks", Proc. of 2017 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HI, USA, pp. 2261-2269, Jul. 2017. [https://doi.org/10.1109/CVPR.2017.243]
• I. Goodfellow, Y. Bengio, and A. Courville, "Deep learning", MIT press, Nov. 2016.
• D. P. Kingma and J. Ba, "Adam: A Method for Stochastic Optimization", arXiv preprint arXiv:1412.6980, , Dec. 2014. [https://doi.org/10.48550/arXiv.1412.6980]
• K. Fukushima, "Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position", Biological cybernetics, Vol. 36, No. 4, pp. 193-202, Apr. 1980. [https://doi.org/10.1007/BF00344251]
• S. Albawi, T. A. Mohammed, and S. A. Zawi, "Understanding of a convolutional neural network", Proc. of 2017 international conference on engineering and technology(ICET), Antalya, Turkey, pp. 1-6, Aug. 2017. [https://doi.org/10.1109/ICEngTechnol.2017.8308186]
• J. Zhuang, T. Tang, Y. Ding, S. C. Tatikonda, N. Dvornek, X. Papademetris, and J. Duncan, "AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients", Proc. of the Advances in Neural Information Processing Systems, Vol. 33, pp. 18795-18806, Dec. 2020. [https://doi.org/10.48550/arXiv.2010.07468]
• S. R. Dubey, S. Chakraborty, S. K. Roy, S. Mukherjee, S. K. Singh, and B. B. Chaudhuri, "diffGrad: An Optimization Method for Convolutional Neural Networks", IEEE transactions on neural networks and learning systems, Vol. 31, No. 11, pp. 4500-4511, Nov. 2020. [https://doi.org/10.1109/TNNLS.2019.2955777]
• S. K. Roy, M. E. Paoletti, J. M. Haut, S. R. Dubey, P. Kar, A. Plaza, and B. B. Chaudhuri, "AngularGrad: A New Optimization Technique for Angular Convergence of Convolutional Neural Networks", arXiv preprint arXiv:2105.10190, , May 2021. [https://doi.org/10.48550/arXiv.2105.10190]
• K. S. Kim and Y. S. Choi, "HyAdamC: A New Adam-Based Hybrid Optimization Algorithm for Convolution Neural Networks", Sensors, Vol. 21, No. 12, pp. 1-41, Jun. 2021. [https://doi.org/10.3390/s21124054]
• W. E. L. Ilboudo, T. Kobayashi, and K. Sugimoto, "Robust Stochastic Gradient Descent With Student-t Distribution Based First-Order Momentum", IEEE transactions on neural networks and learning systems, Vol. 33, No. 3, pp. 1324-1337, Mar. 2022. [https://doi.org/10.1109/TNNLS.2020.3041755]
• A. Krizhevsky and G. Hinton, "Learning multiple layers of features from tiny images", Apr. 2009.
• B. Heo, S. Chun, S. J. Oh, D. Han, S. Yun, G. Kim, Y. Uh, and J. W. Ha, "AdamP: Slowing Down the Slowdown for Momentum Optimizers on Scale-invariant Weights", arXiv preprint arXiv:2006.08217, , Jun. 2020. [https://doi.org/10.48550/arXiv.2006.08217]