[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 19, No. 7, pp.101-112

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 31 Jul 2021

Received 05 Jul 2021 Revised 26 Jul 2021 Accepted 29 Jul 2021

DOI: https://doi.org/10.14801/jkiit.2021.19.7.101

원자로 초소형 내시경의 실시간 영상 잡음 제거 기법

유진호^*

; 천종훈^**

; 박성호^***

; 이지민^****

*국립목포대학교 융합소프트웨어학과 교수
**전남도립대학교 인공지능드론학과 교수
***한전KPS(주) 종합기술원 책임연구원
****조선대학교 SW중심대학사업단 초빙객원교수(교신저자)

A Real-time Image Noise Removal Algorithm for Micro-Endoscope System in Nuclear Power Plants

Jin-Ho You^*

; Jong-Hun Chun^**

; Sungho Park^***

; Jimin Lee^****

Correspondence to: Jimin Lee Dept. of SW Convergence Education Institute, Chosun University, Korea, Tel.: +82-62-230-7853, Email: histhing@chosaun.ac.kr

초록

본 논문에서는 원자로 내 고방사선 구역에 설치된 표준형 증기발생기의 상부번들 내부를 검사하기 위한 초소형 내시경 장치를 통해 전송되는 영상 신호에 유입된 영상 잡음을 실시간에 제거할 수 있는 고속 영상 잡음 제거 알고리즘을 제안한다. Total variation(TV) 최소화기반 영상 잡음 제거 기법은 이미지 경계의 블러링이 적으면서 잡음 제거 성능이 뛰어나다고 평가된다. 본 논문에서는 영상 잡음 제거에 효율적인 smoothing norm 함수와 이 함수를 도입한 TV 손실 함수를 제안한다. 심층신경망 학습에 활용되고 있는 여러 최적화 탐색 기법들을 제안한 TV 손실함수 최소화에 적용하여 비교 분석함으로써 Adamax가 수렴 속도가 빠르고 잡음 제거 성능도 우수함을 보인다. 그리고, 제안한 TV기반 잡음제거 알고리즘 Adamax-TV를 엣지 컴퓨터 수준 GPU에서 구현하여 VGA급 원자로 내시경 영상의 잡음 제거를 15~27fps 속도로 실시간으로 처리할 수 있음을 보인다.

Abstract

In this paper, we propose a high-speed image noise removal module that can remove image noise in real time from image signals transmitted through a microscopic endoscope device to inspect the inside of the upper bundle of a standard steam generator installed in a high radiation area of a nuclear power plant. The total variation (TV) minimization-based image noise removal technique is evaluated to have excellent noise removal performance while reducing image boundary blurring. In this paper, we propose a smoothing norm function for efficient image noise removal and a TV loss function incorporating this function. This paper shows that Adamax has a fast convergence speed and excellent noise removal performance, by applying and analyzing various optimization search techniques used in deep neural network learning to the proposed TV loss function minimization. By implementing the proposed TV-based noise removal algorithm Adamax-TV on edge computer level GPUs, it is shown that the noise removal of the VGA-class image of nuclear reactor endoscope can be processed in real time at a rate of 15 to 27 fps.

Keywords:

Image noise removal, Total variation, Optimization, Micro-endoscope, Nuclear power plant

Ⅰ. 서 론

증기발생기는 원자력발전소 격납용기 내부의 고방사선 구역에 설치되어 1차측(방사능 구역)과 2차측(비방사능 구역)의 압력경계를 이루는 설비로서 전열관 손상 시 1차측의 방사성 물질이 외부로 유출되는 사고로 이어질 수 있다. 따라서, 2차측 구조물 및 내부 이물질 유입 여부를 확인하기 위하여 주기적으로 육안검사를 수행하고 있다[1][2]. 하지만, 증기발생기의 전열관 상부번들 내부를 검사할 수 있는 기술이 없어 전열관 절단을 통해서만이 육안검사 및 이물질 제거를 수행하고 있어 기기관리에 어려움이 있다. 특히 신규원전의 경우 증기발생기의 관막음률이 상승하게 되어 증기발생기 교체주기를 앞당기게 되는 등 원전 운영 측면에서도 큰 어려움을 겪고 있다[2].

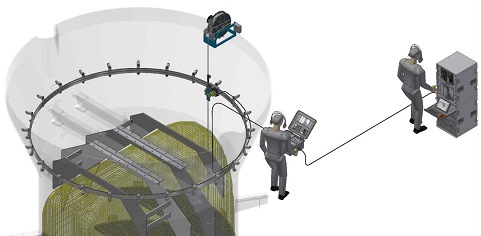
현재 증기발생기 상부 구조물 검사를 위한 내시경 시스템은 두께 2.4mm 이하, 길이 15m 이상, 굴곡 반경 20mm 내외의 유연한 플랫 케이블로 구성되며, 긴 케이블을 통해 아날로그 신호기반 영상신호를 전송하면서 전송 케이블에 유입된 왜란 신호의 유입에 의해 수신된 영상에 잡음이 발생한다.

본 논문에서는 원전 내 고방사선 구역에 설치된 표준형 증기발생기의 상부번들 내부를 검사하기 위한 초소형 내시경 장치를 통해 전송되는 영상 신호에 유입된 영상 잡음을 실시간에 제거할 수 있는 실시간 영상 잡음 제거 기법을 제안한다. 원전 내 내시경 검사 시스템은 휴대 가능성과 외부와 단절된 통신망 환경을 고려하여 개발되어야 한다. 이에 따라 내시경 영상 잡음 제거 모듈도 엣지 컴퓨팅 장치에 탑재되는 수준의 GPU를 사용하여 실시간 영상 잡음제거가 가능하여야 한다. 최근 심층신경망을 활용한 영상잡음제거 기법으로서 DIP-TV[3], DnCNN[4], IRCNN[5] 등 다양한 기법들이 연구되었으며 잡음 제거 후 영상 품질 수준도 높은 편이지만 일반적인 엣지 컴퓨팅 장치에서 초당 15 프레임 이상 실시간 영상 잡음 처리 성능을 내지는 못한다.

Total variation(TV) 최소화기반 영상 잡음 제거 기법은 이미지 경계의 블러링이 적으면서 잡음 제거 성능이 뛰어나다고 평가된다[3][6]-[9].

Fig. 1.

Visual inspection, control system and endoscope device for nuclear power plant

본 논문에서는 기존 TV기반 영상 잡음 제거 알고리즘의 성능을 개선하기 위하여 영상 잡음 제거에 효율적인 smoothing norm 함수와 이 함수를 도입한 TV 손실 함수를 제안한다. 심층신경망 학습에 활용되고 있는 여러 최적화 탐색 기법들을 제안한 TV 손실함수 최소화에 적용하여 비교 분석함으로써 이들 중 Adamax가 수렴 속도가 빠르고 잡음 제거 성능도 우수함을 보인다. 그리고, 제안한 TV기반 잡음제거 알고리즘 Adamax-TV를 엣지 컴퓨터 수준 GPU에서 구현하여 VGA급 원자로 내시경 영상의 잡음 제거를 15~27fps 속도로 실시간으로 처리할 수 있음을 보인다.

본 논문의 구성을 다음과 같다. 2절에서 기존 영상 잡음 제거기법에 대하여 살펴보고, 3절에서는 본 논문에서 제안한 영상 잡음 제거 기법을 소개하고 기술한다. 4절에서는 제안한 영상 잡음 제거 기법을 기존 알고리즘들과 성능을 비교하여 평가한다. 마지막으로 5절에서 결론과 향후 연구에 대하여 기술한다.

Ⅱ. 관련 연구

영상 잡음 제거는 매우 보편적인 영상처리 문제로서 여러 기법들이 연구되어 왔다. 이동평균 필터, 가우시안 필터, FFT, 저주파 필터, bilateral 필터 등의 알고리즘은 고속 처리가 가능한 방법이지만 이미지의 경계가 블러링되는 문제가 있어, 이미지 경계를 보존하면서 잡음만을 제거하는 비등방성 확산 등 최적화기반 잡음제거 연구들이 있었으며[7][8] 그 중 total variation 최적화기반 잡음 제거 알고리즘이 성능이 좋았다[3][6]-[9]. 최근 DIP-TV[3], DnCNN[4], IRCNN[5] 등 CNN기반 심층신경회로망을 활용한 영상 잡음 제거 연구들이 활발하며 영상 잡음 제거 성능 또한 뛰어나다.

DIP-TV[3]는 인코더 합성곱 층과 디코더 합성곱 층의 결합으로 구성된 CNN 심층신경망과 Total Variation 최소화를 결합한 모형이다. 입력 영상에 대한 심층신경망의 출력 결과로부터 계산되는 Total Variation 목적 함수를 최소화하는 ADMM(Alternating Direction Method of Multipliers) 최적화 반복 과정을 통해 영상의 잡음을 제거한다. DIP-TV 알고리즘은 영상 잡음제거 성능이 매우 뛰어나지만 영상 잡음 제거에 2000~3000 epoch가 소요되어 수렴 속도가 매우 느려 실시간 영상처리에는 부적합하다.

IRCNN[5]은 CNN과 ReLU를 결합하여 7층으로 구성한 심층신경망으로서 낮은 수준의 잡음에 대한 영상 복원 능력은 뛰어나지만 학습되지 않은 잡음 수준 또는 높은 수준의 잡음에 대해서는 영상이 왜곡되는 부분이 발생하는 문제가 있다. IRCNN은 GPU GTX 1060기반 시스템에서 12 fps 이하로 처리 속도로서 성능이 낮은 엣지 컴퓨터에서 실시간 동영상 잡음제거에 활용하기에는 다소 부족하다. 24단계의 각 잡음 수준마다 개별적으로 심층신경망을 학습하여 각 모델 데이터들을 저장한 후 잡음 수준에 맞는 모델 데이터를 적용해야 하는 단점이 있다.

Total variation(TV) 기반 영상 정규화 기법은 Rudin[8]에 의해 소개된 이후 잡음 제거 등 영상처리에 활발하게 활용되고 있다. TV 정규화는 현실세계 영상은 주로 지역 국소적으로는 평평하고 부드러우며 전역적으로는 색상, 밝기 등 속성 값들은 완만한 변화를 갖는 영역이 많다는 통계적인 특징에 기반하고 있다[6]. Total variation은 영상의 각 화소 위치에서 색상 농도 등 화소 속성 값의 변화율인 경사도 크기(norm) 값들의 총합으로 나타내진다. 영상에 잡음이 많이 분포할수록 그리고 잡음 수준이 높을수록 TV 값은 커진다. TV 정규화에서 영상의 경사도 크기는 비등방성 확산 효과를 통해 영상의 경계와 세밀한 특징을 보존하는 데 도움이 되도록 L₁ -norm을 사용한다. TV기반 잡음 제거 기법은 입력 영상과 차이가 적으면서 TV 값을 최소화하는 영상을 검색하는 방법이며, 식 (1)과 같이 TV 손실 함수 L(F)를 최소해를 찾는 수치해석 문제로 표현된다[6][8].

F * = arg m i n L F F L F = ∑ F p ∈ F T V F p + λ F p - G p 22 T V F = ∇ F 1 = D x F + D y F

(1)

기존 초기 total variation 최소화 기반 알고리즘들은 최적화 수렴속도가 느려 실시간 영상 잡음 제거에는 적용하기 어려웠다. 그 이유는 적용한 단순 경사하강기반 최적화 알고리즘의 수렴 속도가 느렸고 지역최소화에 빠지는 문제 등이 있었기 때문이다. ADMM-TV[9]는 2-D FFT 변환을 통한 주파수 공간에서 TV기반 잡음제거 기법에 ADMM 최적화 알고리즘을 적용하여 수렴 속도를 증가시키면서 잡음 제거 성능을 높이기도 하였다.

Ⅲ. Adamax 최적화를 적용한 Total Variation 기반 영상 잡음 제어 알고리즘

3.1 논문에서 제안하는 Total Variation Function

본 논문에서는 영상에서 경계 부분은 유지하며 잡음을 효율적으로 제거하는 데 도움을 주는 smoothing norm 함수와 이를 도입한 TV 손실 함수를 제안한다. 본 논문에서 제안하는 영상 잡음 제거를 위한 TV기반 손실 함수 L(F)는 다음 식 (2)와 같이 정의한다.

L F = ∑ F p ∈ F T V F p + λ S ε I β I F p - G p 22 s t . T V F = ω T V 1 F + (1 - ω) T V 2 F, T V 1 F = ∥ ∇ F ∥ 1 = D x F + D y F, T V 2 F = S ε T V β T V (∥ ∇ F ∥ 2) S ε β x = x 2 + ε β

(2)

식 (2)에서 F는 2D 영상 변수, G는 잡음을 포함하는 입력 2D 영상, $S ϵ β x$ 는 smoothing norm 함수이다. TV(F)는 영상 F에 대한 TV 함수이며 TV₁(F)와 TV₂(F) 두 개의 TV 함수의 ω에 대한 가중치 평균이다. TV₁(F)는 영상 F에 대한 그래디언트의 L₁-norm으로 정의된다. TV₂(F)는 F의 그래디언트의 L₂-norm에 smoothing norm $S ϵ β x$ 을 적용한 변형된 TV 함수이다. ∥F-G∥₂는 영상 F와 입력 영상 G와의 차이에 대한 L₂-norm 값으로서 $λ S ε I β I F - G 2$ 는 잡음 제거를 위해 변형된 F가 입력 영상 G에 가깝도록 유지하는 정규화 항이다. λ는 손실함수 L(F)에서 정규항의 비중을 조절하는 계수이다. 영상에서 잡음은 영상 화소 값의 변화를 발생시키며 TV 값을 증가시킨다. TV기반 잡음 제거 알고리즘은 입력영상 G에 가까우면서 TV 값을 줄이는 영상 F를 찾도록 구성한다. 영상 잡음을 최소화하는 F^*는 식 (3)과 같이 L(F)를 최소화하는 것으로 정의된다.

F * = arg m i n L F F

(3)

식 (3)의 최소해는 일반적으로 경사하강법 알고리즘을 통해 찾으며 본 논문에서는 Adamax 최적화 알고리즘을 사용한다.

3.2 Smoothing norm 함수 $S ϵ β x$

Perona와 Malik[7]은 영상에서 경계 특징을 보존하면서 잡음 성분을 효과적으로 제거할 수 있는 비등방성 확산 기법을 이용한 잡음 제거 및 경계 특징 추출 방법을 제시하였다.

많은 잡음을 포함하는 영상 I(x)는 거친 표면을 구성하며 각 점에서의 경사도 크기의 총합은 커지게 된다. 영상 경사도 크기 총합으로 나타내지는 에너지 함수 E[I]는 다음과 같이 정의될 수 있다.

E I = 12 ∫ Ω g ∇ I x 2 d x

(4)

에너지 함수 E[I]를 감소시키는 영상 I(x)의 변화량은 다음과 같다.

∂ I ∂ t = - ∇ E I = d i v g' I x 2 ∇ I

(5)

위 식에서 gʹ는 영상의 경사도 크기에 따라 적용되는 확산 계수 역할을 하며, gʹ이 상수이면 등방 확산이며 상수가 아니면 비등방 확산이 된다. 일반적으로 영상에서 영역간 경계의 경사도는 크고 잡음 점에서의 경사도는 작다.

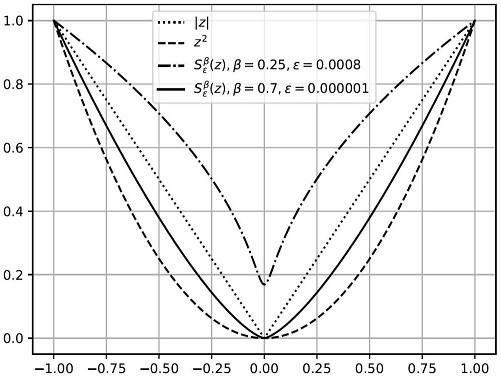
본 논문에서는 그림 2와 같은 특성을 갖는 smoothing norm 함수 $S ϵ β x$ 를 제안한다. 잡음 영역에 해당할 가능성이 높은 낮은 영상 경사도의 화소에서 잡음 제거 평활화가 더 빨리 진행하도록 영상 경사도에 대한 손실함수를 설정한다. β < 0.5이면 $S ϵ β x$ 의 미분은 0에서 멀어질수록 단조 감소한다. β가 0에 가까울수록 $S ϵ β x$ 는 원점 근처에서 가파르며, 작은 크기의 잡음이 더 빨리 평활화되므로 낮은 잡음 수준의 영상 복원에 적합하다. 원본 영상과 복원 영상간 차이에 대한 손실함수는 잡음 평활화로 인한 작은 영상 차이는 허용하고 큰 차이의 변형은 막는 smoothing norm 함수를 적용한다. β > 0.5이면 $S ϵ β x$ 는 L₁- norm보다 완만하며, β > 1이면 L₂-norm보다 더 완만하다. 본 논문에서는 영상 차이에 대한 손실함수로 β = 0.7, ϵ = 0.000001인 $S ϵ β x$ 함수를 사용한다. 이는 L₁- norm과 L₂-norm의 중간 정도가 된다.

Fig. 2.

Smoothing norm function Sϵβx

3.3 기존 경사하강기반 최적화 알고리즘

본 논문에서 제안한 TV 손실함수를 최소화하는 해를 구하는 알고리즘으로 심층신경망의 학습에 많이 사용되고 있는 여러 경사하강법 알고리즘들을 적용하여 실험적으로 가장 수렴속도가 빠르고, 손실함수가 최소화되고 잡음제거 영상의 품질 척도 PSNR, SSIM가 최대화되는 경사하강법 알고리즘을 비교 분석하여 선택한다. 본 논문에서는 Vanilla GD, SGD, RMSprop, Rprop, Adam, Adamax 알고리즘들을 비교한다.

매개변수 θ에 대한 평가함수 J(θ)를 최소화하는 최적해 θ^*는 식 (6)과 같이 표현되며, 최적해를 찾는 다양한 경사하강법 알고리즘들이 개발되었다.

θ * = arg m i n J θ θ

(6)

Vanilla GD(Vanilla Gradient Descent)는 식 (6)과 같이 가장 기초적인 경사하강법으로서 전체 학습 데이터에 대한 그래디언트 ▽_θJ(θ)에 학습률 η를 적용하여 매개변수 θ를 갱신하며, 학습 단계마다 고정된 학습률 η를 적용한다[10].

θ t + 1 = θ t - η • ∇ θ t J θ t

(7)

SGD(Stochastic Gradient Descent)는 Vanilla GD와 같이 학습 단계마다 고정된 학습률 η를 적용하며, 임의적으로 추출된 부분 학습데이터 집합 (x⁽ⁱ⁾,y⁽ⁱ⁾)에 대한 그래디언트 ▽_θJ(θ;x⁽ⁱ⁾;y⁽ⁱ⁾)를 적용한다[10][12].

θ t + 1 = θ t - η • ∇ θ t J θ t; x t i; y t i

(8)

SGD는 각 학습 단계에서 매개변수 수정 벡터가 고정되지 않고 변화됨으로써 지역최소해에 빠지는 문제 등을 보완하여 Vanilla GD에 비해 개선된 최적화 성능을 보인다.

Rprop, RMSprop, AdaGrad, AdaDelta, Adam, Adamax 알고리즘들은 학습 진행 중 학습률을 가변적으로 조절하거나 모멘텀(momentum) 개념을 도입하여 과거 학습량을 반영하여 학습량을 적응적으로 조절함으로써 학습 속도를 향상시킨다.

Rprop[13]은 각 단계에서 그래디언트의 부호가 유지되거나 바뀌는 경우에 따라 학습률을 다르게 적용하는 전략을 사용한다.

α t, t = α t - 1, i • η g r o w if ∇ t, i J θ t • ∇ θ t - 1, t J θ t > 0 α t - 1, i • η s h r i n k if ∇ t, i J θ t • ∇ θ t - 1, t J θ t < 0 α t - 1, i o t h e r w i s e θ t + 1 = θ t - α t s g n ∇ θ t J θ t

(9)

Adagrad[14]는 SGD 알고리즘에 학습률을 가변적으로 조절하며, 현재까지 많이 변화한 매개변수들의 변화를 줄이도록 하여 최적해에 근접할 가능성을 높이고자 한다.

G t = G t - 1 + ∇ θ t J θ t 2 θ t + 1 = θ t - η G t + ε • ∇ θ t J θ t

(10)

RMSProp[15]은 Adagrad의 G_t가 계속증가하면서 학습률이 매우 둔화되는 단점을 보완한 방법으로서 지수평균을 적용하여 G_t를 갱신한다.

G t = γ G t - 1 + 1 - γ ∇ θ t J θ t 2 θ t + 1 = θ t - η G t + ε • ∇ θ t J θ t

(11)

AdaDelta[16]는 RMSProp과 같이 Adagrad를 보완하기 위해 제안된 방법으로서 2차 최적화를 근사적으로 도입하여 학습 속도를 향상시키도록 한다.

G t = γ G t - 1 + (1 - γ) ∇ θ t J θ t 2 ∆ θ t = s t - 1 + ε G t + ε • ∇ θ t J θ t θ t + 1 = θ t - ∆ θ t s t = γ s t - 1 + 1 - γ ∆ θ t 2

(12)

Adam[11]은 RMSProp과 모멘텀 방식을 결합한 형태이다. 최적화 성능이 좋아 심층신경망 학습에 기본적으로 많이 사용하는 방식이다.

m t = β 1 m t - 1 + 1 - β 1 ∇ θ t J θ t υ t = β 2 υ t - 1 + 1 - β 2 ∇ θ t J θ t 2 m^t = m t 1 - β 1 t θ t + 1 = θ t - η v^t + ε m^t

(13)

Adamax[11]는 Adam의 확장형으로서 Adam의 v_t 항에 적용된 L₂-norm을 L_∞-norm으로 확장한 형태를 갖는다.

m t = β 1 m t - 1 + (1 - β 1) ∇ θ t J θ t υ t = max β 2 υ t - 1, ∇ θ t J θ t θ t + 1 = θ t - η υ t m t

(14)

3.4 TV 영상 잡음 제거 적용 최적화 알고리즘 성능 비교 분석

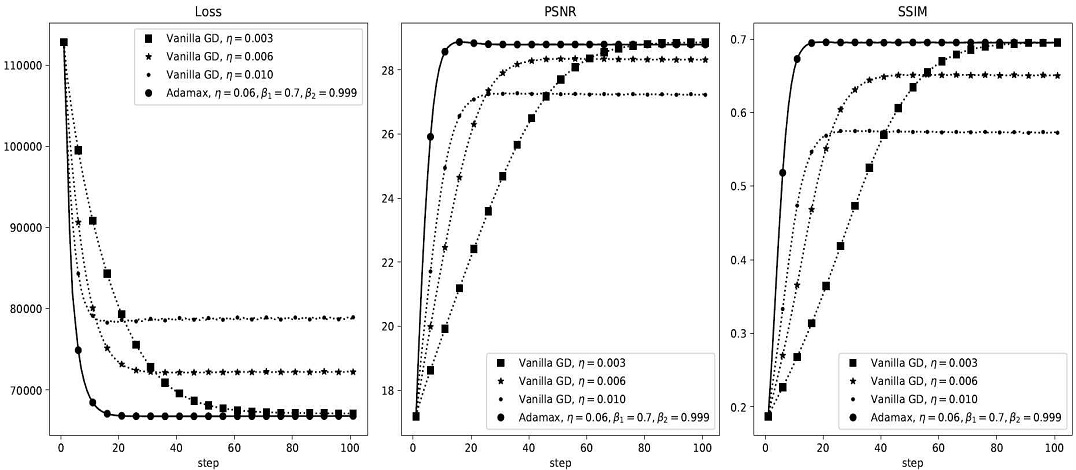
그림 3은 Vanilla GD와 Adamax 알고리즘의 비교이다. Vanilla GD의 학습률은 η = 0.003, 0.006, 0.01을 적용하고 Adamax는 학습률 η = 0.06, β₁ = 0.7, β₂ = 0.999를 적용한 것이다. Adamax가 손실함수 수렴 속도가 빠르며, Vanilla GD의 학습률을 높이면 손실함수 수렴은 빠르지만 손실함수는 더 높은 값으로 수렴되어 잡음 제거 성능이 떨어지게 된다. 다른 경사하강기반 최적화 알고리즘들도 대체적으로 학습률을 높이면 수렴은 빨라지나 최적화 성능은 떨어진다.

Fig. 3.

Comparison of vanilla GD and Adamax optimizer performance

그림 4는 가우시안 잡음의 분산 값으로 정의되는 잡음수준 0.01, 0.02, 0.05를 생성하여 만든 이미지에 대하여 각 최적화 알고리즘을 적용하여 최적화 성능을 비교한 것이다.

Fig. 4.

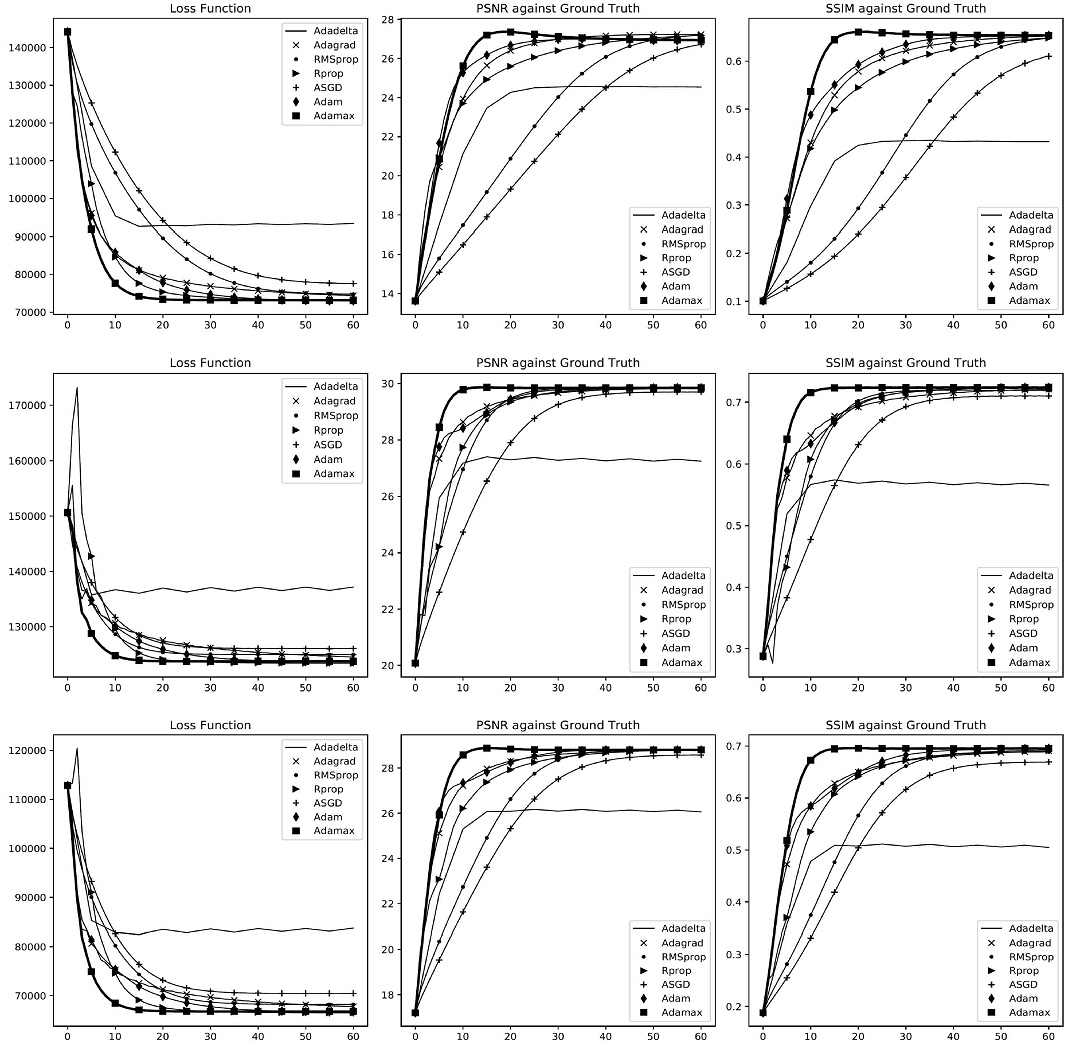
Comparison of TV-based noise reduction convergence speed with Adamax and other optimization algorithms

비교 실험에 사용한 각 최적화 알고리즘에 적용한 매개변수는 다음 표 1과 같다. Adamax-TV와 비교한 각 알고리즘별 매개변수는 잡음제거 실험을 통해 수렴속도를 빠르게 하면서 PSNR, SSIM을 최대화하는 값을 설정한 것이다. 실험한 모든 잡음 수준에서 Adamax 알고리즘의 수렴 속도가 가장 빠르며 손실함수와 PSNR, SSIM 최적화 성능도 가장 좋다. 잡음 수준이 클수록 모든 최적화 알고리즘은 수렴 속도가 느려지고 영상 품질은 떨어지는 데 Adamax는 상대적으로 더 완만하게 느려진다. 이 실험 결과로부터 본 논문에서 제안하는 TV기반 영상잡음제거의 손실함수를 최적화하는 데에는 Adamax가 가장 효율적임을 판단할 수 있다.

Table 1.

Optimzation algorithm parameters

Ⅳ. 영상잡음제거 실험 및 성능 평가

본 논문에서 제안한 Adamax 최적화를 적용한 TV 기반 잡음 제거 알고리즘 Adamax-TV과 ADMM 최적화기반 TV 알고리즘 ADMM-TV, 컨볼루션 심층신경망기반 잡음제거 알고리즘 IRCNN, Bilateral Fiter[17], Guided Filter[18]를 비교 실험하였다.

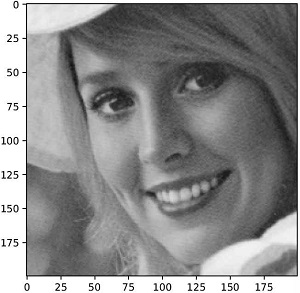
그림 5는 영상 잡음제거 비교 실험에 사용된 원본 영상이다.

Fig. 5.

Original image for comparison

원본 영상에 임의적인 가우시안 잡음을 추가하는 방식으로 잡음영상을 생성하여 각 알고리즘에 적용하였다. 잡음이 제거된 영상과 원본 영상간 PSNR, SSIM 척도를 측정하여 각 알고리즘의 성능을 비교하였다.

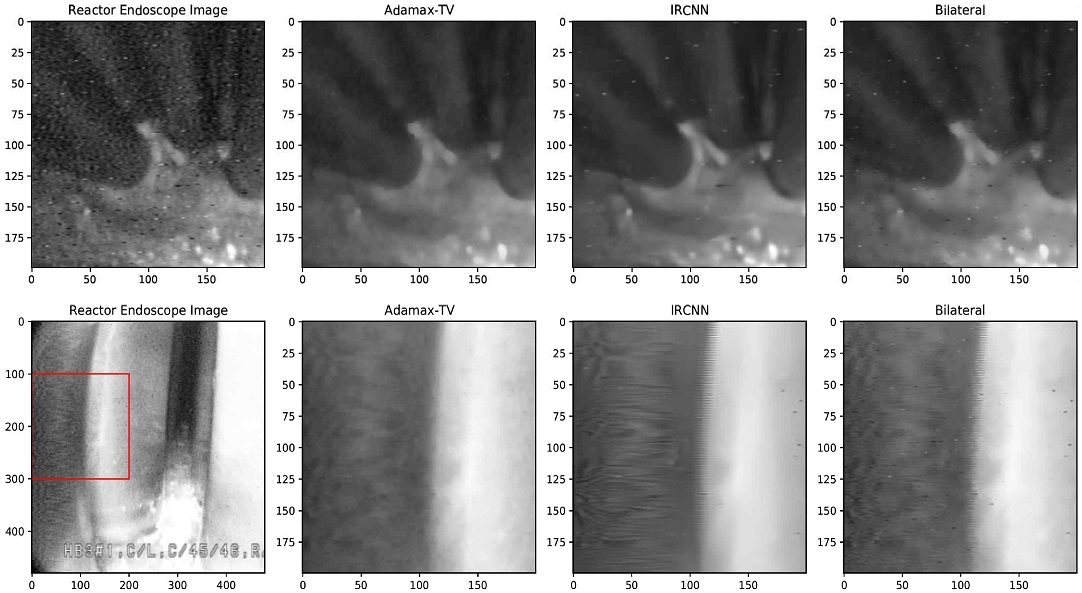
각 잡음수준별 알고리즘의 잡음 제거 성능 결과는 표 2와 같다. 비교 실험에 사용된 영상은 흑백으로서 각 화소값의 범위는 [0, 1]이다. 그림 6, 7은 영상의 잡음 수준(분산) σ² = 0.01, 0.06에서 각 알고리즘이 생성한 잡음 제거 영상을 비교한 것이다. 본 논문에서 제안한 Adamax-TV의 잡음 제거 성능은 전반적인 잡음수준에서 ADMM-TV보다 높음을 알 수 있다.

Table 2.

Comparison of noise removal performance by noise level

Fig. 6.

Micro endoscope system with image noise removal module

Fig. 7.

Noise removed images using Bilateral and Guided filters

심층신경망기반의 IRCNN은 낮은 잡음수준(σ < 0.04)에서는 Adamax-TV보다 높은 성능을 보였으나 높은 잡음수준(σ² ≧ 0.05)에서는 잡음 제거가 잘되지 않았다. Bilateral Filter와 Guided Filter는 매우 낮은 잡음수준(σ = 0.005)에서는 Adamax-TV보다 높은 성능을 보였으나 잡음이 큰 조건에서는 잡음 제거 영상에서 블러링 현상이 크며 PSNR과 SSIM 값도 Adamax-TV 보다 낮았다.

본 논문에서 제안한 영상 잡음제거 알고리즘 Adamax-TV와 IRCNN을 GPU기반 엣지 컴퓨팅 장치에 구현하여 실시간 내시경 영상에 대한 잡음제거 처리 속도를 측정하였다. 실험에 사용된 원자로 초소형 내시경 카메라의 영상 해상도는 640x480 VGA급이며 흑백 영상으로 변환하여 성능 실험을 하였다. 실험에 사용한 엣지 컴퓨팅 장치는 NVidia Jetson Nano, NVidia AGX, NVidia GTX-1060기반 시스템이다. Adamax-TV와 비교 알고리즘 IRCNN 은 python언어로 pytorch와 OpenCV 패키지를 사용하여 구현하였다. 실험 결과 각 장치별 영상 잡음 제거 속도는 표 3과 같다. Adamax-TV는 IRCNN보다 약 2배 이상 빠른 속도를 보였으며 GTX 1060 GPU에서 초당 27 프레임 정도로서 실시간 처리에 충분한 성능을 보인다. 이에 비해 IRCNN은 비디오 영상에 대한 실시간 영상처리에는 다소 성능이 부족하다.

Table 3.

Noise removal processing speeds

본 논문에서는 원자로 증기발생기의 육안검사 시스템에 적용할 2.2mm 직경의 초소형 내시경 카메라와 15m 길이의 영상 전송 케이블로 구성된 내시경 시스템 모듈을 제작하였다(그림 8, 9).

Fig. 8.

Micro endoscope system with image noise removal module

Fig. 9.

Micro endoscope system

초소형 내시경 카메라와 영상전송케이블을 통해 발생된 영상 잡음을 제거하는 영상처리 알고리즘은 GPU를 탑재한 엣지 컴퓨팅 장치에 구현하였다.

그림 10은 구현한 초소형 내시경 시스템으로 촬영한 원본 영상과 본 논문에서 제안한 Adamax-TV 알고리즘과 IRCNN으로 잡음을 제거한 영상이다. Adamax-TV 알고리즘은 초당 27 프레임 속도로 초당 12 프레임인 IRCNN보다 빠르게 잡음을 제거하면서 영상 품질도 좋은 편이다. 그림 9에서 IRCNN과 Bilateral 필터는 제거되지 않은 잡음이 있는 경우가 있고 IRCNN의 경우 부자연스러운 표면을 생성하기도 하는 데 반하여 Adamax-TV가 IRCNN과 Bilateral 필터보다 잡음 평활화를 더 잘하고 있음을 보여준다.

Fig. 10.

Noise reduced video images of nuclear reactor micro-endoscope system

Ⅴ. 결론 및 향후 과제

본 논문에서는 원전 내 고방사선 구역에 설치된 표준형 증기발생기의 상부번들 내부를 검사하기 위한 초소형 내시경 장치를 통해 전송되는 영상 신호에 유입된 영상 잡음을 실시간에 제거할 수 있는 고속 영상 잡음 제거 모듈을 제안하였다. 본 논문에서는 total variation기반 영상 잡음 제거 알고리즘 Adamax-TV를 제안하였다. Adamax-TV 알고리즘은 본 논문에서 제안한 smoothing norm 함수 $S ϵ β$ 를 도입하여 구성한 TV 손실 함수를 최소화하는 Adamax 최적해 탐색 과정으로 구성된다. 제안한 Adamax-TV 알고리즘을 엣지 컴퓨터 수준 GPU에서 구현하여 잡음 제거 성능과 속도를 평가하였다. 실험결과 영상전송 케이블 길이 15m, 직경 2.2mm의 640×480 VGA급 해상도를 지닌 원자로 육안검사용 초소형 내시경 카메라의 영상 잡음 제거를 15~27fps 속도로 실시간으로 처리할 수 있음을 보였다. 또한 본 논문에서는 심층신경망 학습에 널리 사용되고 있는 SGD, RProp, RMSProp, AdaGrad, AdaDelta, Adam, Adamax 최적화 알고리즘들을 제안한 TV기반 손실함수 최적화에 적용하여 수렴 속도와 영상 잡음 제거 성능을 비교하였으며, Adamax가 다양한 잡음 수준에서 수렴 속도가 빠르며 영상 잡음 제거 성능도 우수함을 보였다.

향후 연구에서는 Adamax-TV 알고리즘을 개선하여 Full HD급 고해상도 내시경 영상을 실시간 처리할 수 있도록 계산 속도를 높이는 방법과 영상 잡음 제거 성능을 향상시키는 방법에 대하여 다루고자 한다.

Acknowledgments

본 논문은 2018~2021년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행함(No. 20181510102120)

본 논문은 2021년도 한국정보기술학회 종합학술대회에서 발표한 논문 “원전 내 표준형 증기발생기 내부 검사용 초소형 내시경 장치를 위한 실시간 Total Variation 기반 영상잡음 제거 모듈 개발”을 확장한 것임

References

Hosang Shin, "Steam Generator Regulation Direction", Korea Institute of Nuclear Safety, 2016
Gyung Sub Kim, Seung Keun Baek, Ki Chul Kim, "Steam Generator Secondary Side Inspection Technology Development", The 14th Nuclear Safety Technology Information Conference, 2009.
Liu, Jiaming, Yu Sun, Xiaojian Xu, and U. Kamilov, "Image Restoration Using Total Variation Regularized Deep Image Prior", ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (2019), Brighton, UK, pp. 7715-7719, May 2019. [https://doi.org/10.1109/ICASSP.2019.8682856]
Kai Zhang, Wangmeng Zuo, Yunjin Chen, Deyu Meng, and Lei Zhang, "Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising", IEEE Transactions on Image Processing, Vol. 26, No. 7, pp. 3142-3155, Feb. 2017. [https://doi.org/10.1109/TIP.2017.2662206]
K. Zhang, et al., "Plug-and-Play Image Restoration with Deep Denoiser Prior", in IEEE Transactions on Pattern Analysis & Machine Intelligence, pp. 1-1, Jun. 2021. [https://doi.org/10.1109/TPAMI.2021.3088914]
Linwei Fan, Fan Zhang, Hui Fan, and Caiming Zhang, "Brief review of image denoising techniques", Visual Computing for Industry, Biomedicine, and Art, Vol. 2, No. 2, pp. 7, Jul. 2019. [https://doi.org/10.1186/s42492-019-0016-7]
P. Perona and J. Malik, "Scale-space and edge detection using anisotropic diffusion", in IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 12, No. 7, pp. 629-639, Jul. 1990. [https://doi.org/10.1109/34.56205]
Leonid I. Rudin, Stanley Osher, and Emad Fatemi, "Nonlinear total variation based noise removal algorithms", Physica D: Nonlinear Phenomena, Vol. 60, No. 1–4, p. 259-268, Nov. 1992. [https://doi.org/10.1016/0167-2789(92)90242-F]
Qin, Zhiwei, D. Goldfarb, and Shiqian Ma, "An alternating direction method for total variation denoising", Optimization Methods and Software, Vol. 30, No. 3, pp. 594–615, Jun. 2015. [https://doi.org/10.1080/10556788.2014.955100]
Sebastian Ruder, "An overview of gradient descent optimisation algorithms", arXiv preprint arXiv:1609.04747, , Sep. 2016.
Kingma, Diederik P., and Ba, Jimmy, "Adam: a Method for Stochastic Optimization", International Conference on Learning Representations, San Diego, pp. 1–13, May 2015. https://hdl.handle.net/11245/1.505367
H. Robinds and S. Monro, "A stochastic approximation method", Annals of Mathematical Statistics, Vol. 22, No. 3, pp. 400–407, Sep. 1951. [https://doi.org/10.1214/aoms/1177729586]
A. Mosca and G. D. Magoulas, "Adapting resilient propagation for deep learning", CoRR, Vol. abs/1509.04612, , Sep. 2015.
Duchi, J., Hazan, E., and Singer, Y., "Adaptive Subgradient Methods for Online Learning and Stochastic Optimization", Journal of Machine Learning Research, Vol. 12, No. 7, 2121–2159, Jul. 2011.
Tieleman T. and Hinton, E, "Lecture 6.5 – rmsprop", COURSERA: Neural networks for machine learning, 2012.
Zeiler, M. D. "ADADELTA: An Adaptive Learning Rate Method", arXiv:1212.5701, , Dec. 2012.
C. Tomasi and R. Manduchi, "Bilateral Filtering for gray and color images", Sixth International Conference on Computer Vision, New Delhi, India, pp. 839-46, Jan. 1998.
K. He, J. Sun, and X. Tang, "Guided Image Filtering", IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 35, No. 6, pp. 1397-1409, Oct. 2012. [https://doi.org/10.1109/TPAMI.2012.213]

저자소개

유 진 호 (Jin-Ho You)

1991년 8월 : 전남대학교 전산통계학과(이학사)

1995년 2월 : 전남대학교 전산통계학과(이학석사)

2006년 2월 : 전남대학교 전산통계학과(이학박사)

2017년 8월 ~ 현재 : 국립목포대학교 융합소프트웨어학과 조교수

관심분야 : 임베디드시스템, 최적화, 기계학습, 영상처리, 제어공학, 전력공학

천 종 훈 (Jong-Hun Chun)

1988년 2월 : 조선대학교 전자공학과(공학사)

1990년 2월 : 조선대학교 전자공학과(공학석사)

1996년 2월 : 조선대학교 전기공학과(공학박사)

1999년 3월 ~ 현재 : 전남도립대학교 인공지능드론학과 정교수

관심분야 : RF회로설계, AI드론설계, 5G무선통신시스템, 위성통신시스템

박 성 호 (Sungho Park)

2006년 2월 : 서울과학기술대학교 기계설계자동화공학과(공학사)

2014년 8월 : 한양대학교 기계공학과(공학석사)

2005년 ~ 현재 : 한전KPS(주) 종합기술원 책임연구원

관심분야 : 로봇공학, 기계학습

이 지 민 (Jimin Lee)

2002년 2월 : 전남대학교 정보학부(이학사)

2011년 2월 : 조선대학교 정보통신공학과(공학석사)

2015년 2월 : 조선대학교 정보통신공학과(공학박사)

2014년 ~ 2017년 : 아주통신(주) 기업부설연구소 연구소장

2018년 ~ 현재 :　조선대학교 초빙객원교수

관심분야 : 멀티미디어 영상처리, 패턴인식, 영상검색, 딥러닝, 자연어처리

Noise level (σ²)	Noisy image		Adamax-TV		ADMM-TV		IRCNN		Bilateral filter		Guided filter
Noise level (σ²)	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
0.005	30.00	0.75	32.28	0.79	31.37	0.76	33.16	0.81	32.31	0.79	32.50	0.80
0.01	20.08	0.29	29.82	0.72	28.86	0.69	30.83	0.74	28.94	0.71	29.17	0.72
0.02	17.19	0.19	28.81	0.70	27.83	0.66	29.96	0.72	27.62	0.67	27.83	0.67
0.03	15.55	0.14	28.03	0.67	27.09	0.64	29.07	0.70	27.00	0.65	27.20	0.65
0.04	14.45	0.12	27.71	0.66	26.75	0.63	28.65	0.70	26.65	0.64	26.88	0.64
0.05	13.62	0.10	27.31	0.66	26.35	0.62	26.86	0.61	26.28	0.62	26.50	0.63
0.06	12.97	0.09	26.95	0.65	26.04	0.61	22.91	0.42	25.88	0.61	26.12	0.61