2단계 k-평균 군집화를 활용한 예측 기법을 활용한 미국 주택가격 예측

Ⅰ. 서 론

특정 사건을 대상과 현상의 집합체라고 설정하고 각 집합체의 구성요소들이 시간의 흐름에 따라 상호영향을 준다고 본다면, 이 집합체를 분석하는 데에는 확률적 해석이 필요하다. 분석 주체가 설정한 가정과 정의로부터 출발하는 연역적 접근방식은 시간의 흐름에 따라 발생가능한 상호작용을 제한할 수도 있으므로, 연역적 접근방식에 기반한 모델 설정도 확률적 해석을 포함하는 것이 일반적이다. 이러한 분석방법 중 대표적인 사례가 회귀분석일 것이다. 회귀분석은 각 연구분야마다 존재하는 다양한 이론에 근거하여 변수들 사이의 일정한 관계를 설정한 후, 일정한 관계 수준을 벗어나는 정도를 회귀분석의 오차항으로 간주하여 연구대상의 변수 간 관계를 분석한다. 반면에, 변수들 사이의 사전 지식없이 데이터의 패턴만을 분석하여 분류 또는 예측 작업을 수행하는 머신러닝 기법은 회귀분석에서의 오차항으로 간주되는 부분들도 변수 간 관계를 분석하는데 사용한다.

한편, 머신러닝 기법 중 변수들 사이의 관계를 파악하는 중점을 두는 상기 방법들과 달리 주어진 데이터로부터 새로운 하위 샘플을 추출하여, 이 하위 샘플만을 이용하는 머신러닝 기법들이 있다. 이러한 방법들 중에는 k-최근접 이웃법(k-Nearest Neighbor), k-평균 군집화(k-means clustering, 표/그림에서 kmeans) 등이 대표적이다. 이러한 머신러닝 기법들은 변수들 사이의 관계를 파악하는데 중점을 두기보다는, 분류 또는 예측 대상과 근접한 하위 샘플과의 유사성에 근거하여 분류 및 예측 작업을 수행하는 것이다. kNN은 분류 또는 예측 대상에 근접한 자료들만을 선택한 후 이 선택 자료들의 평균 등으로 추정 값을 분류 또는 예측결과 값으로 간주하는 기법이다. kNN이 예측대상 근방 자료만을 기반으로 분류 또는 예측하는 방법이라면, k-평균 군집화는 주어진 전체 데이터를 적절한 개수의 하위 군집들로 구분하고 분류 또는 예측대상과 유사도가 가장 높은 하위 군집을 기반으로 분류 또는 예측결과를 산출하는 방법이다. 그러므로, kNN과 달리 k-평균 군집화는 주어진 자료 전체의 특징을 고려하는 장점이 있으며, 자료의 개수가 많은 경우에도 쉽게 적용이 가능하다.

평균이라는 값이 주어진 자료를 설명하는 다양한 대푯값 중에서 가장 널리 사용되는 값이므로 k-평균 군집화가 다양한 실용연구에서 사용되고 있으나, 군집화 방법에는 k-평균 군집화 외에도 다양한 방식의 군집화 기법들이 존재한다[1]. k-평균 군집화가 전체 데이터를 일정한 개수의 군집으로 분할한 후 군집화를 수행하는 분할적(Partitional) 군집화 방법 이라면, 반대로 각 관측치를 하나의 군집으로 간주한 후 군집들의 크기를 증가시키는 계층적 군집화(Hierarchical clustering)가 있다. 이 계층적 군집화에는 군집들의 평균 벡터간의 거리를 사용하는 중심(Centroid) 기법 군집화, 군집의 크기를 증가시킬 때 분산의 크기가 작은 방향으로 군집을 형성하는 Ward 기법 군집화, 군집들에 속한 관측치들 간의 최장 거리를 기준으로 하는 완전(Complete) 기법 군집화 등이 있다. 이러한 군집화 기법들은 개별 관측치 간의 거리를 중심으로 군집을 형성하므로 이산형(Discrete) 또는 범주형(Categorical) 자료를 대상으로 주로 분류 정확도를 높이기 위해 제시된 경우가 많았다[2]-[4]. 반면에 예측 작업의 경우, 특히 시계열 자료(Time-series data)의 경우는 분류 작업의 레이블(Label)이 범주형 변수인 것과 달리 연속형 변수이므로 군집의 평균을 사용하는 k-평균 군집화가 사용되는 경우가 많은 편이다[5][6]. 한편, k-평균 군집화의 초기 k값은 보통 10개 내외로 설정되어 최적의 k값을 탐색하는 경우가 대부분으로[7], 보다 세분화된 하위군집을 탐색하는 데에는 제한적이었다. 이에 따라, 본 연구는 전체 데이터로부터 세밀하게 구분된 하위 군집을 생성해내기 위하여 k-평균 군집화 기법을 반복하여 적용하는 방법을 제시한다. 이러한 방식으로 조정된 k-평균 군집화 기법은 세밀하게 추출된 하위 군집을 기반으로 보다 정확한 시계열 자료 예측 성능을 보여줄 수 있을 것이다.

Ⅱ. 이론적 배경

k-평균 군집화 방법이 데이터 마이닝 분야에 도입된 이래로[8], 이 방법은 다양한 분류 및 예측 연구에서 사용되었다. Oyelade et al.(2010)은 학생들의 학업성취도를 예측하는 도구로써 k-평균 군집화 방법을 사용하였다[9]. Nidhees et al.(2017)은 k-평균 군집화 방법을 활용하여 유전자 정보로부터 암의 종류를 예측하였다[10]. Nath et al.(2010)은 특정 여행에 소요되는 여행시간을 k-평균 군집화 방법으로 예측하고 다른 머신러닝 기법의 예측성능과 비교하여 k-평균 군집화 방법의 예측 성능의 우수성을 보였다[11]. Shinde et al.(2015)은 심장마비에 영향을 주는 다양한 요소를 고려하여 심장마비를 예측하는 연구에서 k-평균 군집화 방법를 사용하였다[12]. Kakoudakis et al.(2016)은 상수도망의 수도관 고장을 예측하는 연구에서 k-평균 군집화 방법을 활용하였다[13]. 이예담과 김우성(2018)은 대학생의 학습 적응도를 k-평균 군집화 방법을 활용하여 예측하였으며[14], 이영찬(2011)은 k-평균 군집화 방법을 기업의 성과예측모델 개발에 사용하였다[15].

왕한호(2018)는 신호처리 작업에서 단말기 채널 추정에 필요한 파일럿 신호가 없는 상황에서 데이터 심볼의 특성들에 군집화 기법을 사용하여 단말기의 채널을 추정하였다[16]. Tran Thi Thu Ha et al.(2013)은 MRI 뇌 영상자료로부터 뇌 영역을 분류하는 작업에 k-평균 군집화 방법을 적용하였다[17]. 데이터 기반의 분류 및 예측 작업은 관측치 간의 유사도를 기반으로 이루어지는 경우가 많으므로, 상기 연구들과 같이 k-평균 군집화 방법의 적용범위는 광범위하다고 볼 수 있다. 또한, k-평균 군집화 방법은 비교적 단순한 수학적 모델을 따르고 있으므로, 다양한 방식으로 변경되거나 다른 머신러닝 기법과 함께 사용되기도 하였다.

Chen et al.(2017)은 k-평균 군집화와 결정 나무(Decision tree) 기법을 결합한 방법을 사용하여 당뇨병 발병을 예측하였다[18]. Jamal et al.(2018)은 주성분분석과 k-평균 군집화를 사용하여 유방암 예측 연구를 수행하였다[19]. Benmouizaa & Cheknaneb(2013)은 시간당 태양복사열 전망 연구에서 k-평균 군집화와 신경망 모형(Neural network)을 결합한 기법을 사용하였다[20].

k-평균 군집화 방법은 정확한 분류와 예측을 위하여 주어진 데이터 전체를 해석가능한 특정한 함수형태를 가정하기보다는, 유사한 하위 군집을 우선 추출하는 방식을 취하고 있다. 이에 따라, 부분 군집들의 유사도에 따른 분류 및 예측을 수행하는 k-평균 군집화 방법은 상기 연구들과 같이 의학, 생물학 분야 등에서 활발히 사용되었다. 또한, 특정한 함수형태를 가정하지 않는다는 점에서 k-평균 군집화 방법은 다양한 머신러닝 기법들과 결합되어 실증연구에 적용될 수 있었다.

아울러, 본 연구에서 제안하는 2단계 k-평균 군집화 방법과 관련성이 높은 군집화 방법들이 과거에 제안된 바 있다. 허명회(2000)는 이른바 이중 k-평균 군집화 방법(Double k-means clustering)을 제시하였는데 이 기법의 알고리즘은 k-평균 군집화 방법을 각 군집의 평균과 분산이 수렴할 때까지 반복 적용하는 것으로, 이 연구는 이중 k-평균 군집화 방법을 사용하여 예측오류를 감소된다는 것을 보여주었다[21]. Nanetti et al.(2009)은 분석 대상에서 무작위로 k개의 군집을 선택하고 군집의 중심이 안정화되는 시점까지 군집화를 수행하는 알고리즘의 반복 k-평균 군집화 방법(Repeated k-means clustering)으로 뇌의 영역 간 연결성을 분석하였다. 이 연구에서는 약 1000회 가량의 군집화 작업이 반복되어 분류 결과의 안정성이 높은 것으로 나타났다[22].

Hassan(2018)은 k-평균 군집화의 분석 결과가 초기 k값에 큰 영향을 받는다는 점에 착안하여 군집화 작업 후의 각 군집들의 개수와 크기를 조정하여 적절한 k값을 다시 탐색하는 중첩 k-평균 군집화 방법(Iterative k-means clustering)을 제안하였다[23]. Salman et al.(2011)은 이른바 2단계 군집화(Two stage clustering) 기법을 제안하였는데 이 기법은 첫 번째 단계에서는 주어진 자료의 일부분만을 사용하여 군집의 중심을 탐색하고 두 번째 단계에서 첫 번째 단계에서 추출된 중심을 기반으로 정확한 중심의 위치를 탐색하는 방식으로 군집화 연산 시간을 단축시킬 수 있는 방법이다[24].

또한, Chayangkoon & Srivihok(2016)은 k-평균 군집화에서 초기 k값 설정의 중요성에 착안하여, 우선 EM(Expectation-maximization) 알고리즘으로 k값을 도출한 후 군집화를 수행하는 2층계 군집화(Two step clustering)를 제안하기도 하였다[25].

상기 방법들은 대체로 기존의 k-평균 군집화 방법이 연구자가 임의로 설정한 초기 k값에 의존하는 문제점에 착안하여[7][26], 주어진 자료 전체를 대상으로 k-평균 군집화 방법을 반복 적용하는 방식으로 군집의 안정성[21][22]과 연산 효율성[24]을 도모한 방법들이라고 볼 수 있다. 하지만, 상기 방법들은 주어진 전체 자료를 군집화 대상으로 하고 있어 불규칙한 시계열 자료를 예측하는 데에는 다른 방법이 필요하다고 볼 수 있다. 즉, 불규칙한 시계열 자료가 주어진 경우에는 자료 전체보다는 예측 시점과 근접한 자료들의 특성을 더 많이 고려할 필요가 있는 경우에는 상기 방법들과는 다른 접근 방식이 유효할 수가 있는 것이다. 본 연구에서는 이러한 점에 착안하여, 기존의 k-평균 군집화 방법을 2단계로 반복 적용한 2단계 k-평균 군집화 방법을 제안하고, 이 방법을 사용하여 예측성능이 개선될 수 있음을 실증 데이터로 보이고자 한다. 아울러 k-평균 군집화 방법과 관련된 상기 연구들을 정리하면 표 1과 같다.

Table 1.

Related works

Ⅲ. 연구방법

집합 X = {x_i∈R^d|i = 1,...,N}과 이 집합을 분할한 군집 S_i, i = 1,...,L을 고려하자. k-평균 군집화 방법의 목적함수는 식 (1)과 같다.

여기서 ω_ik는 x_i가 S_k에 속하는 경우 1이고 아닌 경우에는 0이며, μ_k는 군집 S_k의 평균이다.

k-평균 군집화 방법은 식 (1)의 목적함수를 최소화하는 군집들 S_k를 찾는 것이다. 즉, k-평균 군집화 방법은 군집 내(Within-cluster) 분산을 최소화하는 방식을 따르고 있으며, 이에 따라 관측치와 군집의 평균 간의 거리는 유클리디안(Euclidean) 거리이다. 물론, 데이터의 속성에 따라 다양한 거리척도가 사용되어 분류 또는 예측에서 다른 결과가 도출 될 수 있다[26][27].

초기 k값은 연구마다 임의로 주어지거나 10개 내외에서 탐색되는 경우가 많다. 하지만, 데이터의 크기가 크거나 하위 군집 내의 변동이 큰 경우에는 이와 같은 k값의 초기 설정은 정확한 분류나 예측에 적절하지 않을 수 있다. 반면에, k값의 초기값을 큰 값으로 설정하면, 연산 규모가 커지므로 비효율적이다[28]. 또한, k값이 큰 경우에는 분류 또는 예측의 목표값과 근접한 군집뿐만 아니라, 목표값과 거리가 먼 군집들도 식 (1)을 최소화하는 문제에 포함해야 하므로 목표값의 정확한 분류 또는 예측의 정확성이 낮아질 수 있다.

이에 따라, 본 연구에서는 예측 목표값과 근접한 군집만을 고려하는 2단계 k-평균 군집화 방법(Two stage k-means clustering)을 사용하여 예측 정확성을 확보하고자 하였다. 이 방법을 활용한 예측 방법은 다음과 같다.

우선, N+1번째의 값을 예측하는 문제에서 첫 번째로 k-평균 군집화 방법을 초기 k값을 2부터 L까지 수행하여 J가 가장 최소화되는 K개의 군집을 얻었다고 하자. 이 군집들 중에서 N+1번째와 가장 가까운 군집, 즉 시계열 자료 예측의 문제에서는 K번째의 군집인 S_K를 고려하자. 그러면, 이 군집은 M개의 데이터를 갖는 새로운 집합 S_K = {x_j∈R^d|j = 1,...,M, M < N}이 된다. 이 S_K를 k-평균 군집화 방법을 재차 적용할 새로운 집합으로 간주하고 식 (1)을 사용하면 우리는 새로운 군집 $$ {S_i}^{\text{'}}$$, i = 1,...,L^ʹ을 얻을 수 있다. 이 새로운 군집들 중에서 예측 목표인 N+1번째 자료와 가장 근접한 군집을 S_K라고 하면, 최종 예측값은 이 S_K^ʹ을 기반으로 얻어질 수 있다.

S_K^ʹ는 전체 데이터를 처음부터 KK^ʹ개의 군집으로 나누어 얻어진 군집들과는 차이가 있는데, 이는 두 번째 k-평균 군집화 방법을 수행하는 과정에서 첫 번째 k-평균 군집화 방법에 의해 얻어진 S_K를 제외한 나머지 군집들은 고려되지 않기 때문이다. 즉, 2단계 k-평균 군집화 방법은 총 (K+K^ʹ)개의 군집화 과정만을 수행하여 S_K^ʹ를 얻을 수 있는 것이다. 아울러, S_K^ʹ은 1단계 군집화에서 얻은 군집들 중에서 예측 목표와 가장 가까운 S_K 군집만을 고려하여 얻어지므로 예측 정확성을 높이는데 유용할 수 있다. 이상의 2단계 k-평균 군집화 방법을 전체적으로 정리하면 그림 1과 같다.

Fig. 1.

Two stage k-means clustering outline

아울러, 2단계 k-평균 군집화 방법 알고리즘은 그림 2와 같다.

Fig. 2.

Two stage k-means clustering algorithm

Ⅳ. 분석결과

본 연구에서 제안한 2단계 k-평균 군집화 방법의 예측성능을 검증하기 위하여 사용된 데이터는 미국의 주택가격 관련 자료이다. 종속변수는 미국의 신규 판매주택가격(Price)이며 독립변수는 주택담보대출이자율(Mort)과 월별신규주택공급수(Supp)이다. 주택은 하나의 경제적 재화로써 수요과 공급에 따라서 가격이 결정되므로 월별신규주택공급량은 주택가격에 영향을 주는 중요한 요소라고 할 수 있다.

또한, 주택을 구매할 시 주택구매자가 현금을 충분히 보유하는 것은 일반적으로 드문 경우이며, 유동성 보유 목적의 현금의 기회비용 또한 주택구매자에 따라 다를 수 있다. 이에 따라, 주택을 구매할 시 주택담보대출이 대부분 이용되며, 주택담보대출의 이자율은 주택구매 여부 및 주택 가격에 영향을 주게 된다. 이와 같이 경제학적 수요와 공급 측면에서 주택가격과 밀접하게 연관된 주택공급수와 주택담보대출 이자율은 주택가격을 안정적으로 예측하는데 중요한 변수라고 볼 수 있다.

신규 판매주택가격은 미국에서 판매된 신규 주택가격의 중위값으로 미국의 주택도시개발부에서 매월 발표되는 자료이다. 주택담보대출이자율은 대출기간이 30년인 주택담보대출의 고정금리로써 미연방준비제도에서 매주 발표되는 자료이다. 월별신규주택공급수는 미국에서 실제 판매된 주택 대비 시장에 공급된 주택 수로 미국의 주택도시개발부에서 매월 발표하고 있다. 자료 수집기간은 1980년 1월부터 2019년 12월까지이며, 예측은 2007년 7월부터 2019년 12월까지의 기간을 3구간으로 구분하여 수행되었다.

데이터의 기술통계량은 표 2와 같다. 신규판매주택가격과 주택담보대출이자율은 표준편차(STD)가 평균의 1/2 수준으로 변동성이 심한 편으로 보인다. 반면에, 월별신규주택공급수는 표준편차가 평균의 1/4인 수준으로 비교적 안정된 양상을 보인다. 이것은 신규판매주택가격과 주택담보대출이자율이 가격변수인 반면에, 월별신규주택공급수는 실제 주택의 거래량 변수인 점에 기인한다고 볼 수 있다.

Table 2.

Descriptive statistics

2단계 k-평균 군집화 방법의 예측 성능을 확인해보기 위하여 기본적인 최소자승법(OLS) 및 다양한 머신러닝 기법과 비교를 하였다. 머신러닝 기법 중 LASSO는 일반적인 선형회귀 분석 시 발생할 수 있는 과적합(Overfitting) 문제를 완화할 수 있는 방법으로 알려져 있는데[29]. 이는 LASSO를 통한 회귀계수는 조정 파라미터(Tuning parameter)를 통하여 일반적인 선형회귀에 의한 회귀계수보다 적게 추정되기 때문이다. 이를 통하여, LASSO는 주어진 데이터에 대한 설명력만을 고려함으로써 발생할 수 있는 과적합 문제를 완화할 수 있다.

OLS나 LASSO가 한 가지의 회귀 모형을 추정하는데 중점을 둔다면, 서포트벡터머신(Support Vector Machine, 표/그림에서 SVM)은 독립변수들을 활용하여 주어진 종속변수를 최대한 분류하는데 중점을 두는 머신러닝 기법이다. SVM은 독립변수들을 구분하는 함수식을 설정하고, 이에 따라 종속변수를 얼마나 잘 분류하고 예측하는지에 따라 함수식을 결정하는 방법이다. SVM에서 쓰이는 함수식은 주로 독립변수 간의 거리함수로 복잡한 모델을 설정할 필요가 없다. 본 연구에서는 SVM을 회귀모형에 적용한 서포트벡터회귀(Support vector regression)를 사용하였다[30].

신경망(Neural Network) 모형은 데이터의 특성을 고려하거나 특정한 함수식을 설정하지 않고 독립변수를 반복적으로 조합하여 새로운 변수를 생성해내는 방법으로 예측성능을 높이는 기법이다. 즉, 신경망 모형은 독립변수에 가중치를 부여하여 은닉층(Hidden layer)을 생성하고, 이 은닉층들을 종속변수에 적합시켜 예측성능이 가장 높아지는 시점까지 이 과정을 반복하는 것이다. 특히, 최근에 신경망 모형들 중에서 각광받고 있는 순환 신경망(Recurrent Neural Networks, 표/그림에서 RNN) 모형은 입력 값들로부터 은닉상태(Hidden state)를 생성할 때 이전 시점의 은닉상태를 반영하기 때문에 시계열 자료와 같은 순차적 데이터를 분석하는데 많이 활용되고 있다[31][32].

본 연구에서는 이러한 순환 신경망 모형을 비교 예측기법에 포함하였다. 아울러, 2단계 k-평균 군집화 방법과 비교 예측기법으로 기존의 k-평균 군집화와 중심 기법 군집화(Cencl), Ward 기법 군집화(Wcl), 완전 기법 군집화(Comcl) 등을 포함하여 예측 결과를 비교하였다.

본 연구에서 군집화에서 사용한 군집수는 자료의 규모를 고려하여 1개에서 20개 사이의 군집수 중에서 가장 예측력이 높은 군집수를 매 예측시기마다 선택하여 사용하였으며 군집화 이후 군집 내의 평균값을 2단계 k-평균 군집화 방법의 예측치로 설정하였다. 2단계 k-평균 군집화 방법과 다른 예측기법들의 예측성능을 비교하기 위하여 평균절대비오차(Mean Absolute Percentage Error, MAPE)를 사용하였다. MAPE는 식 (2)와 같다.

여기서, N은 예측 수, y_i는 실제값, f_i는 각 기법들의 예측값임.

표 3은 각 예측기법들의 MAPE값을 구간별로 나타낸 것이다. 이 논문에서 제안하는 k-평균 군집화 방법은 모든 구간에서 가장 낮은 MAPE값을 보여주어 예측성능이 가장 높은 것으로 나타났다.

Table 3.

MAPE(%) comparison

k-평균 군집화 방법의 경우는 첫 번째 구간에서는 높은 예측성능을 보여주었으나 나머지 구간들에서는 다른 예측기법들과 비슷한 수준의 예측성능을 보였고, 중심 기법 군집화(Cencl), 완전 기법 군집화(Comcl), Ward 기법 군집화(Wcl) 방법들은 구간마다 k-평균 군집화 방법보다 높은 예측성능을 보이는 경우도 있었으나 2단계 k-평균 군집화 방법(Proposed)보다 높은 예측성능을 보여주진 못하였다.

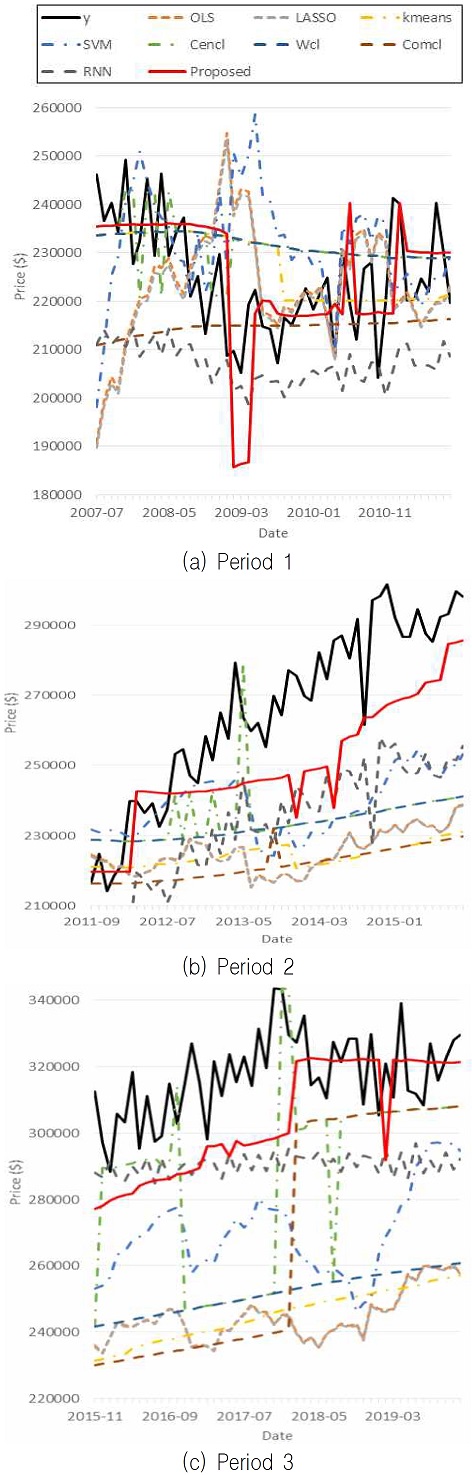
그림 3은 2단계 k-평균 군집화 방법과 다른 머신러닝 기법의 예측값들을 실제 신규 판매주택가격과 시계열상에서 비교한 것이다. 그림 3에서와 같이 실제 신규 판매주택가격(y)은 시계열에 따라 단조증가 또는 단조감소하지 않고 변동성이 큰 모습을 보이므로 일반적인 선형모형으로 실제 신규 판매주택가격을 예측하기에는 어렵다고 볼 수 있다. 반면에 전체 자료를 설명하는 선형모형보다는 이러한 큰 변동성에 주목하여 자료를 군집화하여 해석하고 예측하는 접근법이 실제 신규 판매주택가격을 예측하는데 유용하다고 볼 수 있다.

Fig. 3.

Predicted values by the prediction methods

3구간에서 모두에서 검은색으로 표시된 실제 신규 판매주택가격에 붉은색으로 표시된 2단계 k-평균 군집화 방법의 값이 전반적으로 다른 예측값들보다 근접한 것을 확인할 수 있었다. 노란색 쇄선으로 표시된 k-평균 군집화 방법과 2단계 k-평균 군집화 방법의 예측값 양상이 다른 것은 예측 목표값 근방에서 더욱 정확한 예측을 가능하게 하는 하위 군집이 존재한다는 것을 의미하며, 2단계 k-평균 군집화에 따른 그래프가 k-평균 군집화의 그래프보다 변동이 심한 것은 이 하위 군집의 적은 표본수에 기인한다고 볼 수 있다. 아울러, 표 3에서 첫 번째 구간에서는 k-평균 군집화와 2단계 k-평균 군집화의 예측성능이 다른 예측기법 대비 높은 것으로 나타났다.

이것은 그림 3의 첫 번째 구간 그래프에서와 같이 실제 신규 판매주택가격이 단조성을 보이지 전혀 보이지 않는 불규칙한 추세를 보임에 따라 특정 함수식을 포함하는 예측기법들보다 군집의 평균만을 사용하는 군집화 기법들의 예측성능이 높은 것이라고 해석이 가능하며 이러한 모습은 중심 기법 군집화(Cencl), Ward 기법 군집화(Wcl), 완전 기법 군집화(Comcl) 방법들의 비교적 낮은 MAPE값에서도 확인할 수 있다.

2단계 k-평균 군집화 기법이 k-평균 군집화보다 적은 수의 자료를 사용한다는 것을 감안하면 이 결과는 고무적이라고 볼 수 있다. 이는 2단계 k-평균 군집화는 실제 값을 예측하는데 유용한 자료들만을 군집화하여 예측값의 편의를 감소시켜 낮은 MAPE값을 산출하는 것으로 볼 수 있기 때문이다[19].

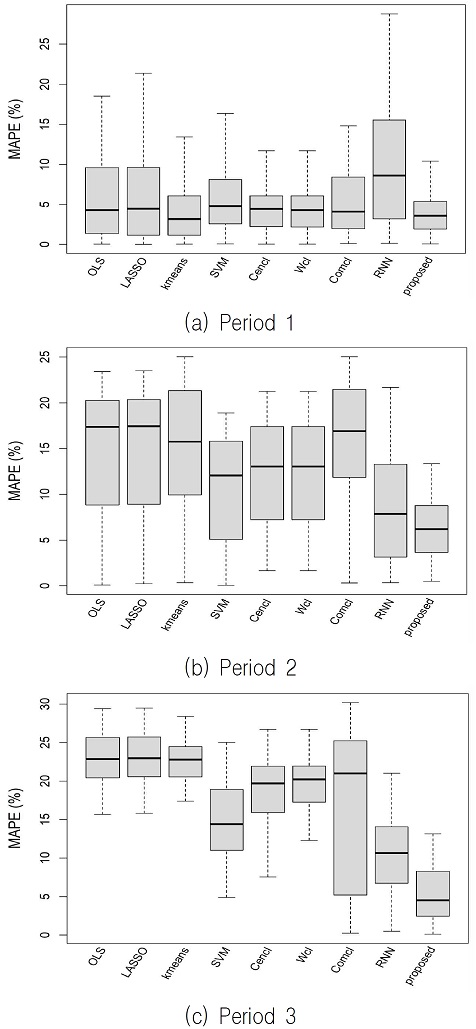
그림 4는 각 예측기법의 예측성능을 비교하기 위하여 MAPE를 상자그림(Boxplot)으로 나타낸 것이다. 3구간 모두에서 2단계 k-평균 군집화는 다른 예측기법에 비해 낮은 MAPE를 보여 그림 3의 결과와 부합하였다. 또한, 그림 4로부터 MAPE 값의 분산정도를 알 수 있으며 이것은 예측성능의 안정성과 연관된다고 볼 수 있다.

Fig. 4.

Boxplot comparison of MAPE

2단계 k-평균 군집화의 경우 첫 번째 구간에서 분산정도가 다른 예측기법들보다 상당히 낮은 것으로 나타났으며 다른 구간에서도 다른 예측기법들 대비 분산정도가 낮은 수준으로 나타났다.

Ⅴ. 결론 및 향후 과제

변수들간의 관계를 모두 고려하여 특정한 함수식을 기반으로 하는 예측기법은 충분한 데이터 확보여부, 연구에서 다루지 못한 외부 변수 등 다양한 요소에 의해 언제나 높은 예측성능을 담보하기는 쉽지 않다. 반면에, 머신러닝은 변수들간의 사전 지식 없이 주어진 데이터의 특성에만 기반한 예측기법이다. 특히, 머신러닝 기법 중 주어진 데이터에서 서로 유사한 하위 샘플을 군집화하여 분류 및 예측 작업을 수행하는 k-평균 군집화는 널리 쓰이는 머신러닝 기법으로 알려져 있다. 기존 연구들에서 k-평균 군집화의 초기 k값은 임의로 설정되는 경우가 많아 보다 세분화된 하위 군집에 기반한 예측에는 제한적인 부분이 있었다. 본 연구는 기존의 k-평균 군집화에서 얻어진 하위 군집에 다시 k-평균 군집화를 적용하여 예측 대상값과 보다 근접한 세분화된 하위 군집에 기반한 2단계 k-평균 군집화 예측기법을 제시하였다.

2단계 k-평균 군집화의 예측성능을 검증하기 위하여 다양한 머신러닝 기법과의 MAPE를 비교하였다. 실증 검증을 위하여 2단계 k-평균 군집화 및 비교 예측기법을 활용하여 미국의 신규 판매주택가격을 예측하였다. 분석결과, 2단계 k-평균 군집화는 다른 예측기법보다 낮은 MAPE를 보여 높은 예측성능을 나타내었다. 특히, 세분화된 하위 군집으로 사용된 자료의 개수가 상대적으로 부족함에도 불구하고 MAPE의 분산된 정도가 낮아 비교적 안정된 예측성능도 보여주었다.

본 연구에서 제시한 2단계 k-평균 군집화는 일반적인 군집화 방법과 마찬가지로 사용의 용이성을 지니고 있으며, 예측 대상이 되는 실제 값에 보다 근접한 군집을 탐색한다는 점에서 이론적인 직관성도 가지고 있다. 이에 따라, 변수들의 관계가 기존에 엄밀하게 증명되지 않은 경우의 실용적인 연구에서 본 예측 기법은 사용될 수 있다고 볼 수 있다. 특히, 본 연구에서 사용된 주택가격과 같이 불규칙한 시계열 자료 예측 연구 등에서 활용성이 높을 것으로 기대된다. 아울러, 2단계 k-평균 군집화 방법은 상대적으로 적은 관측치들로 예측을 수행함에도 불구하고 MAPE가 분산된 정도가 비교적 낮으므로 실무에서의 활용성이 높다고 볼 수 있다. 예를 들어, 자료수집을 위한 충분한 조사가 이루어지지 못하는 경우에 주어진 자료를 우선 군집화한 후 예측 대상에 가장 근접한 군집에 대해서만 추가 조사를 실시하여 2단계 군집화 방법을 적용할 수 있다. 이와 같이 2단계 k-평균 군집화 방법은 자료가 부족한 상황에서 의사결정이 필요한 경우에도 적은 양의 자료에 기초하여 안정적인 예측치를 제공할 수 있는 것이다.

2단계 k-평균 군집화는 기본적으로 k-평균 군집화을 기반으로 이루어지므로 기존의 연구와 같이 초기의 k값을 적절히 잘 설정하는 것이 중요하다고 볼 수 있다. 이론적으로는 주어진 데이터의 개수만큼 k값을 설정할 수 있으나, 군집내의 자료 개수가 추정 파라미터 대비 적을수록 예측오차의 분산이 커진다는 단점이 있다. 특히, 2단계 k-평균 군집화는 2단계의 군집화 과정을 거쳐야 하므로 k값의 상한이 기존의 k-평균 군집화보다 더 적게 결정된다. 이러한 점은 일반적인 k-평균 군집화보다 초기 k값을 더 적은 범위에서 설정할 수 있다는 점에서 알고리즘을 수행하는데 효율적인 부분이라고 볼 수 있다. 한편, 2단계 k-평균 군집화는 각 군집화 단계마다 k값의 상한을 동일하게 설정한다면 자료의 개수가 최소 k²이 되어야 하므로 소규모 자료가 주어진 연구에는 적용의 한계점이 있다. 이와 관련하여, 자료의 크기가 상당히 큰 경우에는 더 높은 단계의 군집화도 가능하므로 자료의 크기와 군집화 반복횟수 간의 분석적 접근도 향후에는 의미있는 연구가 될 수 있을 것으로 기대된다.

Acknowledgments

이 논문은 2020년도 강릉원주대학교 신임교원 연구비 지원에 의하여 연구되었음

References

• M. A. Tayal and M. Raghuwanshi, "Review on various clustering methods for the image data", Journal of Emerging Trends in Computing and Information Sciences, Vol. 2, pp. 34-38, Jun. 2010.
• Dorman, Karin S and Maitra, Ranjan, "An Efficient $ k $-modes Algorithm for Clustering Categorical Datasets", arXiv preprint arXiv:2006.03936, , Jun. 2020.
• Agarwal, Parul, Alam, M. Afshar and Biswas, Ranjit. "A hierarchical clustering algorithm for categorical attributes", In: 2010 Second International Conference on Computer Engineering and Applications. IEEE, pp. 365-368, Jan. 2010. [https://doi.org/10.1109/ICCEA.2010.222]
• Alalyan, Fahdah, Zamzami, Nuha, and Bouguila, Nizar, "Model-based hierarchical clustering for categorical data", In: 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE). IEEE, pp. 1424-1429, Jun. 2019. [https://doi.org/10.1109/ISIE.2019.8781307]
• Lin, J., Vlachos, M., Keogh, E., and Gunopulos, D., "Iterative incremental clustering of time series", In International Conference on Extending Database Technology, Springer, Berlin, Heidelberg, pp. 106-122, Mar. 2004. [https://doi.org/10.1007/978-3-540-24741-8_8]
• Huang, X., Ye, Y., Xiong, L., Lau, R. Y., Jiang, N., and Wang, S., "Time series k-means: A new k-means type smooth subspace clustering for time series data", Information Sciences, 367, pp. 1-13, Nov. 2016. [https://doi.org/10.1016/j.ins.2016.05.040]
• F. Cai, N.-A. Le-Khac, and M.-T. Kechadi, "Clustering Approaches for Financial Data Analysis", in Conference: 8th International conference on Data Mining, Nevada, USA, Jul. 2012.
• J. MacQueen, "Some methods for classification and analysis of multivariate observations", in Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, Vol. 1, No. 14: Oakland, CA, USA, pp. 281-297, Jan. 1967.
• O. Oyelade, O. O. Oladipupo, and I. Obagbuwa, "Application of k Means Clustering algorithm for prediction of Students Academic Performance", International Journal of Computer Science and Information Security, Vol. 7, No. 1, pp. 292-295, Feb. 2010.
• N. Nidheesh, K. A. Nazeer, and P. Ameer, "An enhanced deterministic K-Means clustering algorithm for cancer subtype prediction from gene expression data", Computers in biology and medicine, Vol. 91, pp. 213-221, Dec. 2017. [https://doi.org/10.1016/j.compbiomed.2017.10.014]
• R. P. D. Nath, H.-J. Lee, N. K. Chowdhury, and J.-W. Chang, "Modified K-means clustering for travel time prediction based on historical traffic data", in International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Springer, pp. 511-521, Sep. 2010. [https://doi.org/10.1007/978-3-642-15387-7_55]
• R. Shinde, S. Arjun, P. Patil, and J. Waghmare, "An intelligent heart disease prediction system using k-means clustering and Naive Bayes algorithm", International Journal of Computer Science and Information Technologies, Vol. 6, No. 1, pp. 637-639, Feb. 2015.
• K. Kakoudakis, K. Behzadian, R. Farmani, and D. Butler, "Pipeline failure prediction in water distribution networks using evolutionary polynomial regression combined with K-means clustering", Urban Water Journal, Vol. 14, No. 7, pp. 737-742, May 2017. [https://doi.org/10.1080/1573062X.2016.1253755]
• Y. D. Lee and W. S. Kim, "Prediction of college student adaptability to class using K-means clustering and support vector machine", Proceedings of the Conference of Korean Operations Research and Management Science Society, pp. 1055-1060, Apr. 2018.
• Y. C. Lee, "Clustering-based Performance Prediction Model Using Technology Rating Data", Journal of The Korean Data Analysis Society, Vol. 13, No. 3, pp. 1471-1482, 2011.
• Hanho Wang, "Performance Evaluation of Channel Estimation Scheme Using Clustering Algorithm", The Journal of Korean Institute of Information Technology, Vol. 16, No. 2, pp. 61-66, Feb. 2018. [https://doi.org/10.14801/jkiit.2018.16.2.61]
• Tran Thi Thu Ha, Jin Young Kim, Seungho Choi, "Automated MRI Brain Extraction Using K-means Clustering and Anisotropic Diffusion Filter", The Journal of Korean Institute of Information Technology, Vol. 11, No. 12, pp. 115-122, Dec. 2013. [https://doi.org/10.14801/kiitr.2013.11.12.115]
• W. Chen, S. Chen, H. Zhang, and T. Wu, "A hybrid prediction model for type 2 diabetes using K-means and decision tree", in 2017 8th IEEE International Conference on Software Engineering and Service Science (ICSESS), IEEE, pp. 386-390, Beijing, China, Nov. 2017. [https://doi.org/10.1109/ICSESS.2017.8342938]
• A. Jamal, A. Handayani, A. Septiandri, E. Ripmiatin, and Y. Effendi, "Dimensionality reduction using pca and k-means clustering for breast cancer prediction", Lontar Komput. J. Ilm. Teknol. Inf, pp. 192-201, Dec. 2018. [https://doi.org/10.24843/LKJITI.2018.v09.i03.p08]
• K. Benmouiza and A. Cheknane, "Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models", Energy Conversion and Management, Vol. 75, pp. 561-569, Aug. 2013. [https://doi.org/10.1016/j.enconman.2013.07.003]
• M. H. Huh, "Double K - Means Clustering", The Korean Journal of Applied Statistics, Vol. 13, No. 2, pp. 343-352, Dec. 2000.
• L. Nanetti, L. Cerliani, V. Gazzola, R. Renken, and C. Keysers, "Group analyses of connectivity-based cortical parcellation using repeated k-means clustering", Neuroimage, Vol. 47, No. 4, pp. 1666-1677, Jun. 2009. [https://doi.org/10.1016/j.neuroimage.2009.06.014]
• Ismkhan, Hassan, "I-k-means?+: An Iterative Clustering Algorithm Based on an Enhanced Version of the k –means", Pattern Recognition, Vol.. 79, pp. 402.-413, Jul. 2018. [https://doi.org/10.1016/j.patcog.2018.02.015]
• Salman, Raied, Kecman, Vojislav, Li, Qi, Strack, Robert and Test, Erick, "Two-Stage Clustering with k-Means Algorithm", Communications in Computer and Information Science, Vol. 162, pp. 110-122, Jan. 2011. [https://doi.org/10.1007/978-3-642-21937-5_11]
• Chayangkoon, N. and Srivihok, A., "Two Step Clustering Model for K-Means Algorithm", Proceedings of the Fifth International Conference on Network, Communication and Computing – ICNCC, Dec. 2016. [https://doi.org/10.1145/3033288.3033347]
• A. Singh, A. Yadav, and A. Rana, "K-means with Three different Distance Metrics", International Journal of Computer Applications, Vol. 67, No. 10, Apr. 2013. [https://doi.org/10.5120/11430-6785]
• E. Xing, M. Jordan, S. J. Russell, and A. Ng, "Distance metric learning with application to clustering with side-information", Advances in neural information processing systems, Vol. 15, pp. 521-528, Dec. 2002.
• S. A. Fahad and M. M. Alam, "A modified K-means algorithm for big data clustering", International Journal of Science, Engineering and Computer Technology, Vol. 6, No. 4, p. 129, Apr. 2016.
• T. Hastie, R. Tibshirani, and J. Friedman, "The elements of statistical learning: data mining", inference, and prediction, Springer Science & Business Media, pp. 24, 398. Feb. 2009
• V. Cherkassky and Y. Ma, "Practical selection of SVM parameters and noise estimation for SVM regression", Neural networks, Vol. 17, No. 1, pp. 113-126, Jul. 2004. [https://doi.org/10.1016/S0893-6080(03)00169-2]
• Tokgoz, Alper and Unal, Gozde, "A RNN based time series approach for forecasting turkish electricity load", In: 2018 26th Signal Processing and Communications Applications Conference (SIU). IEEE, pp. 1-4, May 2018. [https://doi.org/10.1109/SIU.2018.8404313]
• Lee, Tae Hyeong and Jun, Myung-Jin, "Prediction of Seoul House Price Index Using Deep Learning Algorithms with Multivariate Time Series Data", SH Urban Research & Insight 8(2), pp. 39-56, Aug. 2018. [https://doi.org/10.26700/shuri.2018.08.8.2.39]