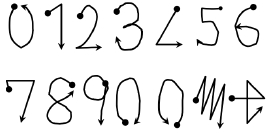다차원 평가를 통한 관성 측정 장치 활용 손 동작 구간 탐지
초록
관성 측정 장치를 활용한 다양한 동작 인식에서 주요한 역할을 하는 동작 구간 탐지를 위해 다변량 에너지 기반 방법론을 제안한다. 다변량 에너지 기반 방법론의 핵심인 다변량 에너지의 구성을 위해, 기계학습의 특징점 선정 기법을 활용해 최적의 가속도 특징벡터를 선정한다. 기존 문헌에서 사용된 6개 특징의 시계열 데이터에 초점을 맞추어 8차까지 증가시키며 이들을 결합 후, 각 999개와 99,999개의 특징 후보에 대해 동작구간과 비동작구간의 변별력을 4가지 목적 함수로 검증한다. 최종 선정된 2가지 후보에 대해 다층퍼셉트론과 방사형 기저함수를 사용하여 최종 검출 성능을 확인하고, 4가지 기존 방법론과 성능을 비교하여 제안하는 방법의 우수성을 검증한다. 가속도와 가속도의 1차/ 2차 미분의 절대값으로 구성되는 협소한 특징점 공간과 비선형 방사형 기저함수가 결합될 때 가장 훌륭한 성능을 보여준다.
Abstract
A new multivariate energy-based motion segmentation has been proposed for various motion recognition using inertial measurement units. For multivariate energy construction, a key process in multivariate energy-based approaches, feature selection in machine learning is used to find the optimal acceleration feature vector. Focusing on the time series of basic features in conventional researches, the separability of 999 and 99,999 feature candidates made from the time series combination is tested with four objective functions. The two finally selected candidates are verified with a multilayer perceptron and a radial basis function, and the results are compared with four conventional methods. It reveals that a narrower feature space bounded by absolute values of acceleration, 1st and 2nd derivatives shows the best record when it is fed to a non-linear radial basis function.
Keywords:
IMU, motion segmentation, gesture recognition, machine learningⅠ. 서 론
동작을 통한 사람 - 컴퓨터간 상호작용(HCI, Human Computer Interaction)에서 관성 측정 장치(IMU, Inertial Measurement Unit)를 활용한 다양한 동작 인식 결과물이 소개되었다[1]-[6]. 그림 1은 일반적인 동작 인식 처리 과정을 보여주는데 동작 구간 탐지는 동작 인식 처리 과정의 필수 처리 과정이며 유입되는 가속도 및 자이로스코프 신호를 이용, 동작을 포함하는 관심 구간을 검출해내는 처리이다. IMU의 경우 반응속도가 빠른 가속도가 널리 사용되며 따라서 동작 구간 탐지는 가속도 신호에 대한 끝점 검출과 동일하다.
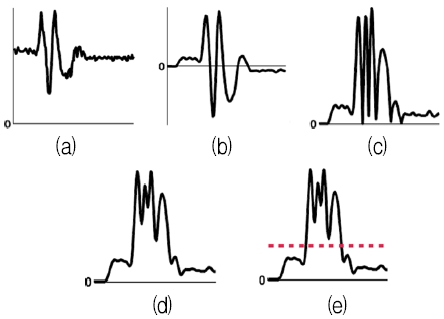
문헌상의 관련 연구를 통해 도출한 동작 구간 검출 과정은 바이어스제거, 에너지계산, 신호평탄화, 문턱값적용 단계로 구성된다[7]. 각 처리단계는 가속도계 활용시 발생하는 제약에 일대일로 대응하며 개발되었으며 이 제약사항은 다음과 같다. 첫째, 동작 인식에 주로 미세 전자기계 시스템 공정을 통해 생산된 초소형 IMU가 사용되는데 일정시간 사용시 열에 의한 바이어스 오류(abias)가 발생한다(그림 2(a)).
둘째, 가속도계는 중력방향과 가속도계 간 각도차의 영향으로부터 자유롭지 못하다. 또한, 사용자 동작에 의해 초기 각도에서 편차가 발생하는데 이로 인한 중력성분의 변화가 위 바이어스 오류와 함께 표류오류가 되어, 이를 극복하기 위해 바이어스 제거와 다양한 형태의 에너지가 제안된다(그림 2(b)(c)). 셋째, 각 에너지는 지역 극대값(Local peak)이 다수 등장하는 다중계곡구조(그림 2(c))를 가져 동작 구간(motion state, m1)과 비동작 구간 (non-motion state, m0)의 선형 분리가 불가능 해진다. 따라서 각 계곡을 메우는 평탄화 처리 과정이 뒤따른다(그림 2(d)).
이때, 손 동작의 경우 동작의 크기가 작아 다중계곡구조의 계곡이 더 깊어진다. 평탄화된 에너지에 문턱값을 적용해 동작 구간을 검출함으로써 목표가 달성된다(그림 2(e)).
다양한 연구가 소개되었으나 생성된 에너지의 차원에 근거해 단변량 에너지 기반 연구와 다변량 에너지 기반 연구로 구분한다. 그림 2는 단변량 에너지 기반 연구의 예시로서, 가속도계의 열오류와 중력의 영향을 최소화하는 새로운 형태의 에너지를 주로 제안한다. 가속도(a(t))의 제곱(a2(t))이나 절대치(|a(t)|)를 에너지로 사용하는 단순한 방식은 중력에 치명적이라 분산 혹은 표준편차를 사용해 부분 선형 근사화를 시도하거나[2], 미분치의 절대값(|Δa(t)|)으로 대체되었다. 단변량 에너지 연구의 차별성은 다채로운 에너지 평탄화 기법에서 두드러진다. 3축의 가속도 신호 또는 기타 신호와 축별 합산을 하거나[3], 비활성구간을 설정해 계곡을 건너뛰거나[4], 신호의 연속적인 두 지역 극대값 사이의 최대값으로 해당 구간을 부분 선형보간하는 등의 기법[5]이 소개되었다. 이러한 시도에도 불구하고 에너지 평탄화의 실패에 대비해 여러 기법들이 중복적으로 사용되어, 결과적으로 동작 구간 탐지 처리 시간이 증가하는 부작용을 낳았다.
증가한 시간지연에 대한 대안으로 다변량 에너지 기반 연구가 제안되었다. 주로, 다변량 에너지 생성 후, 해당 에너지의 다차원 공간에 선형 혹은 비선형 결정경계를 적용해 동작 구간을 검출한다. 일반적으로 HCI의 최적 시간지연은 150-200ms로 보고되었으며[8], 동작 구간 탐지는 동작 상호작용의 일부 알고리즘이라 최대 150ms의 시간 지연을 넘지 않아야 한다.
다변량 에너지 기반 연구는 시간지연의 주요 원인인 신호평탄화 과정을 생략하여 처리 시간이 단축된다. 결국 다변량 에너지 기반 접근법의 다변량 에너지와 선형/ 비선형 경계는 머신러닝의 특징점과 인식기와 같으며, 특징점과 결정경계의 선택이 성능을 좌우하는 요소이다. 문헌상 초기에 보고된 연구[6]에서 특징점은 {a(t), a(t-1), Δa(t)}이며 가속도 에너지의 현재 샘플과 직전 샘플, 그리고 둘의 차이, 즉 미분치로 구성되고 베이지안 인식기(Bayesian Classifier, BC)가 사용되었다. 이후 연구에서 가속도 a(t)와 가속도의 1차미분 Δa(t), 2차미분 Δ2a(t), 그리고 그들의 절대값 |a(t)|, |Δa(t)|, |Δ2a(t)|에 대한 특징점 선택을 통해 Δa(t), |Δa(t)|이 가장 주요한 에너지며, {a(t), |Δa(t)|, Δ2a(t), Δa(t), Δa(t-1),⋯, Δa(t-5)}를 다변량 에너지로 제안하고 BC, k 최근접이웃법 (k Nearest Neighbor, kNN), 다층퍼셉트론(MLP, MultiLayer Perceptron), 방사형 기저함수(RBF, Radial Basis Function network) 등으로 성능을 검증했다[9]-[11].
본 논문은 특징점 조합시 Δa(t), |Δa(t)|의 시계열만을 고려하던 기존 연구의 한계를 넘어서, 앞서 소개한 6개의 성분 모두의 시계열 조합을 특징점으로 고려하고 이에 대한 비선형 모델 인식기로 구성한 다변량 에너지 기법을 제안한다. 정확도 만을 고려하던 기존 방식에서 벗어나 다차원 평가법으로 성능의 우수성을 검증하는 것을 또다른 목적으로 한다.
Ⅱ. 평가 기준, 특징점 선택 및 모델 선택
2.1 평가 기준
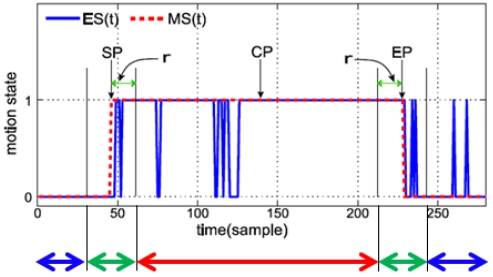
동작 구간 검출의 성능은 그림 3에서 보듯, 수작업으로 표시된 동작 레이블(Motion Segment, MS(t), 붉은색 점선)과 알고리즘으로 검출한 결과(Estimated Segment, ES(t), 푸른 실선)의 일치도를 정확도로 표현한다. 그러나 동작 구간 검출의 목적이 정확한 끝점(Start Point, End Point)을 찾는 것이며 구간 내에서 발생하는 오류는 동작 구간 검출의 실패를 뜻하고 정확도는 이를 적시하지 못한다.
그림 3에서 붉은 화살표 구간에서 발생하는 False Negative 오류가 동작 불연속점이며 동작의 크기가 작은 손 동작 검출에서 흔하게 발생하는 문제이다. 이를 구체화하기 위해 정확도, 불연속점 발생율, 불연속점 최대길이, 시간 지연, 사용된 축의 개수를 평가요소로 하는 다차원 평가법이 제안되었다[7].
2.2 특징점 선택(Feature selection)
다변량 에너지에 기반한 실시간 동작 구간 검출은 적합한 다변량 에너지의 구축과 해당 에너지에 근거해 m1, m0를 판단하는 이진 인식기의 설계에 달려있다.
다변량 에너지의 구축을 위해 기계학습의 특징점 선택이 적용된다. 특징점 후보 집합(Subset)을 구성하기 위한 기본원소(Basic Variable, BV)와 BV의 시계열로 구성된 시계열원소(Time Series Variable, TSV)가 표 1에 주어진다. TSV2.2는 BV의 현재 시점, t부터 2 샘플 이전, t–2까지 취득한 BV의 시계열을 뜻한다. 사전 연구를 통해 우리는 TSV가 BV에 비해 더 높은 변별력을 갖고 TSV와 BV의 결합이 동작유무 분별력을 향상시킴을 확인했다. 그러나 TSV는 현재 시점으로부터 과거 데이터를 메모리에 저장해야 하므로 알고리즘의 시간지연을 증가시킨다. 따라서 TSV를 고려한 특징점 선택은 동작 유무 분별력과 시간지연 크기를 결정한다.
두 단계에 거쳐 특징점을 선정하는데 1차로 BV간 변수를 조합해 {BV1}, {BV2}, ⋯, {BV1, BV2, BV3, BV4, BV5, BV6}에 이르는 총 64개의 후보 집합을 구성하고 이에 대해 2개의 목적함수(Objective function)를 적용하여 클래스간 변별력을 점검한다. 2차로, 앞서 선정된 2개의 우수 후보 집합을 구성한 BV의 시계열 변수 TSV의 차원을 1차부터 8차까지 증가시키며 다시 후보 집합을 조합 하고 이를 2개의 다른 목적함수로 최종 변별력을 확인한다.
특징점 우수 후보 집합을 선정하기 위해 우리는 4개의 선형/ 비선형 목적함수를 사용한다. 인식기와 독립적인 평가방법을 사용하는 Filter 방법을 1차 선정에, 인식기의 인식률로 직접 특징점 후보 집합을 선정하는 Wrapper 방법을 2차 선정에 사용한다. 이는 후보 집합의 변수가 증가할수록 높은 성능을 보이는 편향이 나타나는 Wrapper 방법에 대비한 조치이다. 선형 필터로 다중상관계수 (Multiple Correlaton Coefficient, MCC)를, 비선형 필터로 상호의존정보 (Mutual Information, MI)를 사용하고 Wrapper 방법의 선형 인식기로 BC를, 비선형 인식기로 kNN을 선택한다. BC와 kNN은 인식기의 모델 선택이 용이하다. 최종 선정된 특징벡터에 주성분분석 등의 차원축소는 시도되지 않는데 현재 고려중인 BV간 상관도가 높기 때문이다. 목적함수에 대한 자세한 설명은 [11]을 참고하기 바란다.
2.3 모델 선택(Model selection)
다변량 에너지 기반 접근법은 단변량 에너지를 다변량 에너지로 확장함으로써 생성된 다차원 공간에 투사된 에너지 샘플을 확률적 추정치로 변환한다. 지금까지 진행해온 연구 결과를 반영해 최종 인식기로서 입력-은닉-출력의 3층 MLP와 RBF를 선택했다[9][10]. 모델 선택의 편이를 위해 network topology와 활성화함수에 다음과 같은 제약을 둔다. 은닉층을 1개로, 입력층은 특징점의 차원과 동일하게, 출력층의 노드는 1개로 제한한다. MLP의 활성함수는 은닉층과 출력층 모두에 시그모이드 함수로 삼고 RBF는 은닉층을 위해 가우시안 함수를, 출력층은 시그모이드를 사용한다. 출력층의 최종 출력은 0과 1 사이의 확률값으로 도출되는데 이는 시그모이드 함수의 출력결과와 같다.결국 모델 선택은 은닉층의 노드 수 결정으로 축약되는 효과를 갖는다. MLP와 RBF는 식 (1)~(4)에 주어진다. 입력층의 노드 수가 m, 은닉층의 노드 수가 n 이며, w와 b, x는 각각 가중치, 편향, 입력벡터를 뜻한다. 최종 출력은 반올림 되어 0과 1로 출력된다.
| (1) |
| (2) |
| (3) |
| (4) |
Ⅲ. 실험 및 결과
3.1 실험 설계
실험을 위해 2차에 걸린 데이터 수집을 진행하였다. 1차로, 7명(남 4, 여 3)의 피험자가 3차원 공간에서 그린 그림 4의 필적을 가속도계로 3차례, 총 294개(51406샘플)를 수집하였다. 이때, m0와 m1를 구분하는 MS(t)는 피험자가 버튼을 눌러 기록했다. 가속도계의 샘플링 주파수는 100Hz, 양자화 비트는 8비트, 채널은 x, y, z 축에 할당된 3개이다. 98개씩 3개로 분할하여 학습세트, 검증세트, 사용자종속세트로 각각 할당하고 특징점과 모델 선택에 사용했다. 2차로 동일한 방법으로 12명(남 6, 여 6)으로부터 168개의 데이터(31196 샘플)를 수집하여 이를 사용자독립세트로 할당, 기존 방법론과 성능을 비교하는데 사용했다. 가속도 신호는 x, y, z축의 3채널로 입력되는데 (x+y+z)/3하여 1채널의 신호로 만들었다. 공통적으로 DC 제거와 저주파통과 필터를 적용하였고 이로 인해 발생한 알고리즘상 시간지연은 150ms이다.
3.2 특징점 선택
총 64개의 특징점 후보 집합에 대한 1차 특징점 분석 결과 우리는 ={BV2, BV4, BV6}과 ={BV1, BV2, BV3, BV4, BV5}를 선택했다. MCC의 경우 BV2와 BV4가 강한 변별력을 보이며 특히 BV2가 타 변수, BV1, BV3, BV4, BV5의 허브 역할을 하는 것으로 분석됐다. MI는 BV2, BV4, BV6의 결합이 가장 강한 변별력을 보였으며 BV4가 핵심 변수로 분석됐다. MCC와 MI가 선정한 가장 높은 순위의 후보를 1차 후보로 선정했다.
, 를 구성하는 BV로 범위를 좁힌 후 이들의 TSV로 조합한 999개와 99,999개의 후보 집합에 대해 진행한 2차 선정의 결과로 ={TSV2.0, TSV4.8, TSV6.3}과 ={TSV1.0, TSV3.5, TSV4.8, TSV5.0}을 최종 후보로 선정했다(표 2).
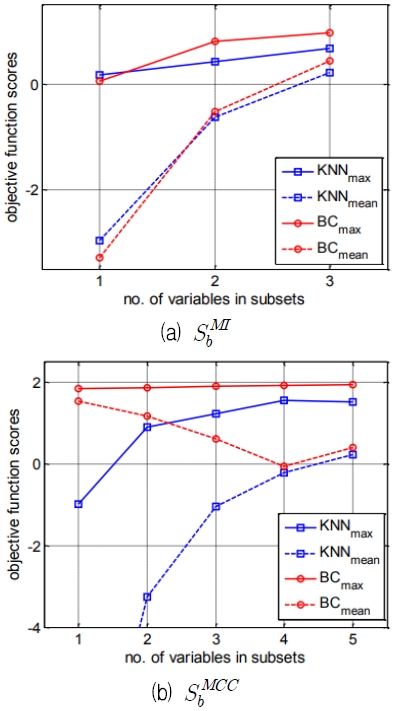
그림 5는 특징점 후보 집합을 구성시 차원을 증가시킨 한 개의 TSV보다 다른 TSV와 결합하면 변별력이 향상됨을 보여준다. 의 경우 결합된 TSV가 증가할수록 변별력 평균이 줄어드는데 이는 TSV3과 TSV5는 BC의 인식률을 저해하기 때문으로 분석되었다. 그럼에도 불구하고 BC의 최대 변별력은 5개의 변수가 모두 결합되었을 때 달성되었다. kNN이 BC에 비해 결합된 TSV의 개수에 민감했으며 변별력도 높았다. 따라서 kNN에 의해 선정된 후보를 최종 특징점 후보 집합으로 선택했다.
3.3 모델 선택
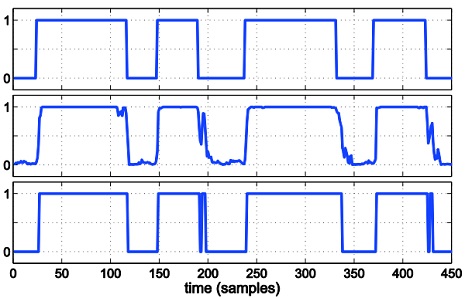
MLP와 RBF를 설계하기 위하여 학습률은 0.05, 손실함수는 최소 제곱 오차, 최적화는 확률적 경사 하강법을 사용하였다. 이때 과적합을 피하기 위해 학습세트와 검증세트를 활용하였다. 은닉층의 노드수는 입력층의 노드 수 × 1/3개부터 입력층의 노드 수 × 3개까지 증가시키며 가장 높은 인식율을 기록하는 노드 수를 선정하였다. 그림 6의 1단은 학습에 사용한 MS(t), 2단은 학습된 신경망의 출력 결과, 3단은 이를 반올림한 결과를 보여준다.
표 3에 주어진 사용자종속세트에 대한 다차원 평가는 성공적인 특징점/ 모델 선택에 대한 통찰을 보여준다. 좀더 협소한 특징점 공간을 갖춘 특징점 후보, , 와 더 포용력있는 비선형 인식기, 39개의 은닉 노드 수를 갖는 RBF가 결합될 때 가장 훌륭한 성능을 보여준다. 는 TSV2, TSV4, TSV6의 결합이며 이들 변수는 모두 절대값 연산을 포함하여 특징점의 분포를 0과 양수로 제한한다. 이로 인해 축소된 공간 상에서 얻어진 정확도 오차(100-acc)와 동작 불연속점 비율(UMBR)이 보다 작고 최대 불연속점 길이(UMBL)는 유사하거나 짧았다. 정확도 오차(100-acc)로만 평가하면 MLP는 RBF보다 우월하나 동작 불연속점 비율에서 MLP가 더 많은 동작 불연속점을 생산함을 보여준다. 이것이 다차원 평가법을 사용하는 이유이다.
또한 은닉층의 노드수에서 MLP(10, 5)는 RBF(39, 44)에 비해 약소한데, 이는 MLP가 m1, m0의 경계에 과적합은 피하였으나 과편향되었다 판단한다.
3.4 기존 알고리즘과 성능 비교
설계된 신경망의 성능 검증을 위해 기존 단변량 에너지 기반 방법론 3개와 다변량 에너지 기반 방법론 1개의 성능을 비교 분석했다. 중력에 강인한 에너지 계산을 위해 처음으로 이동분산을 사용한 [3], 2개 이상의 축에서 계산한 [3]의 에너지를 하나의 에너지로 합병하는 [4], 데이터 마이닝기법을 사용하여 동작 구간 검출 성능은 훌륭하나 시간지연이 큰 [6], 초기 제안된 다변량 에너지기반 방법론, [8]을 선택했으며 이들 모두는 학습세트와 검증세트를 이용해 학습 후, 사용자독립세트로 최종 성능을 비교하였다.
표 4는 본 논문이 제안한 다변량 방법론의 우수성을 확인시켜준다. 제안된 방법으로 설계된 신경망은 [4]와 유사한 불연속점 비율을 기록하고 시간 지연은 절반 이상 단축시킨다.
[6]이 가장 낮은 불연속점 비율을 보이나 알고리즘 상 슬라이딩 윈도우의 크기가 가변적으로 변해, 시간지연 역시 고정적이지 않고 최악의 경우엔 200ms 이상의 시간지연이 발생한다. [3]의 불연속점 비율이 축별 합산으로 줄어든 결과를 [4]의 불연속점 비율로 확인할 수 있으며, [8]의 시간지연은 최소화되나 최악의 불연속점 비율과 최대 불연속점 길이를 기록하였다. [8]의 열악한 성능은 우수한 다변량 에너지 선택이 해당 방법론에 끼치는 영향력을 증명한다.
IV. 결 론
본 논문은 IMU를 활용한 다양한 동작 인식 방법론에서 필수적인, 특히 동작의 크기가 작은 손 동작에 특화된, 동작 구간 검출 방법을 제안한다. 실시간 사용을 목적으로, 시간지연을 최소화하며 동작 구간 검출 능력을 최대화시키기 위해 다변량 에너지 기반 방법론을 제안한다. 기계학습의 특징점 선정을 도입해 새로운 다변량 에너지를 제안하고 이에 대한 신경망 모델을 설계, 구현하였다. 끝으로, 4개의 기존 방법론과 성능을 비교해 제안된 방법론의 우수성을 검증하였다. 제안된 알고리즘은 다차원 평가법으로 분석 결과, 8.40%의 샘플단위오류, 11.90%의 불연속점 발생율, 110ms의 불연속점 길이, 90ms의 시간지연을 기록하였다. 이는 기존 방법에 비해 불연속점 발생율은 유사하나 불연속점 길이와 시간 지연에서 가장 빠른 결과이다.
References
-
Dong-soo Cho et al. "Analysis of Hangul Handwriting Pattern Recognition Using Inertial Measurement Unit", Journal of KIIT, Vol. 13, No. 10, pp. 163-170, Oct. 2015.
[https://doi.org/10.14801/jkiit.2015.13.10.163]

-
Benbasat et al. "An inertial measurement framework for gesture recognition and applications", International Gesture Workshop, Springer, Berlin, Heidelberg, 2001.
[https://doi.org/10.1007/3-540-47873-6_2]

- Eun-Seok Choi et al. "Beatbox music phone: gesture-based interactive mobile phone using a tri-axis accelerometer." 2005 IEEE International Conference on Industrial Technology. IEEE, 2005.
- Won-Chul Bang et al. "Self-contained spatial input device for wearable computers", Seventh IEEE International Symposium on Wearable Computers, 2003. Proceedings. IEEE Computer Society, 2003.
- Lim, Jong Gwan, Young Il Sohn, and Dong Soo Kwon, "Real-time accelerometer signal processing of end point detection and feature extraction for motion detection", 10th IFAC/IFIP/IFORS/IEA Symposium on Analysis, Design, and Evaluation of Human-Machine Systems, 2007.
- Paul-Valentin Borza, "Motion-based Gesture Recognition with an Accelerometer", Ph. D. thesis, Babes-Bolyai University, Faculty of Mathematics and Computer Science, 2008.
-
Jong Gwan Lim, Jaehong Kim, and Dong-Soo Kwon, "Multidimensional evaluation and analysis of motion segmentation for inertial measurement unit applications", Multimedia Tools and Applications, Vol. 75, No. 18, pp. 10907-10934, 2016.
[https://doi.org/10.1007/s11042-015-2812-1]

-
Hiroshi Nittono, "Event-related brain potentials corroborate subjectively optimal delay in computer response to a user’s action", International Conference on Engineering Psychology and Cognitive Ergonomics. Springer, Berlin, Heidelberg, 2007.
[https://doi.org/10.1007/978-3-540-73331-7_63]

-
Jong Gwan Lim, Sang-Youn Kim, and Dong-Soo Kwon, "Pattern recognition-based real-time end point detection specialized for accelerometer signal", in Proceeding of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics(AIM2009), pp. 203-208, Singapore, 2009.
[https://doi.org/10.1109/AIM.2009.5230013]

- Jong Gwan Lim, Sang-Youn Kim, and Dong-Soo Kwon, "Real-time end point detection specialized for acceleration signal", in Proceeding of ICROS-SICE International Joint Conference 2009 (2009 ICCAS-SICE), pp. 5331-5335, Fukuoka, Japan, 2009.
-
Jong Gwan Lim, Mi-hye Kim, and Sahngwoon Lee, "Empirical validation of objective functions in feature selection based on acceleration motion segmentation data", Mathematical Problems in Engineering, Vol.2015, Article ID 280140, 2015.
[https://doi.org/10.1155/2015/280140]


2016년 2월 : KAIST 기계공학(공학박사)
2017년 3월 ~ 현재 : 목원대학교 지능로봇공학과 교수
관심분야 : HRI, 영상/신호처리, 머신러닝