Stacked Bidirectional과 Stacked Unidirectional LSTM을 활용한 주별 전력부하예측
초록
본 연구에서는 주별전력부하 예측을 위해서 LSTM 모형을 활용하였다. LSTM 모형은 단방향(Unidirectional) 또는 양방향(Bidirectional)인지와 단층(Single-layer) 또는 심층(Stacked)인지에 따라서 모형을 세분화시켜 구축하였다. 입력변수로는 전력부하에 영향을 미치는 기상요인과 날짜요인 그리고 전력시차항 등을 다양하게 반영하였다. 표본 외 예측기간은 주별 예측에서 가장 중요한 동절기(1월)와 하절기(8월)를 택했다. 따라서 2018년 1월과 8월 그리고 2019년 1월과 8월에 대해서 각각 주별예측을 실시하였다. 구축한 LSTM 모형들의 예측력을 검증할 벤치마크 모형으로는 MLP 모형을 구축하였다. 예측결과, LSTM 모형이 2018년과 2019년에 대해서 평균적으로 모두 MLP 모형보다 예측력이 좋은 것으로 나타났다.
Abstract
In this paper, the LSTM models were used to predict weekly loads. The LSTM models were constructed by subdividing the model according to whether it was Unidirectional LSTM or Bidirectional LSTM or single-layer LSTM or stacked LSTM. The input variables reflect various weather factors, Calendar factors, and lagged terms that affect weekly loads. The out of sample forecasts periods were the most important winter season (January) and summer season (August) in the weekly forecasts. Therefore, weekly forecasts were made for January and August 2018 and January and August 2019, respectively. The MLP model was established as the benchmark model to verify the predictive power of the LSTM models deployed. The result shows that LSTM models are more predictive performance than MLP model in 2018 and 2019 on average.
Keywords:
load forecasting, unidirectional lstm, bidirectional lstm, single-layer lstm, stacked lstmⅠ. 서 론
본 연구에서는 주별 전력부하예측을 위해 신경망 모형을 활용하였다. 신경망 모형의 경우 최근 예측 분야에서 많이 활용되는 기법으로서 입력층과 출력층 사이에 은닉층이 존재하는 MLP 모형과 순차적 데이터를 처리하는데 적합한 LSTM(Long-Short Term Memory) 모형 등이 있다. 이러한 신경망 모형들은 소프트웨어와 하드웨어의 급속한 발전과 빅데이터의 활용도가 높아지면서 점차 그 중요성이 더 높아지고 있는 추세이다.
실제로 MLP 모형과 LSTM 모형은 예측과 분류 문제를 해결하는데 다양하게 활용되고 있다. 그 예로, 주가 예측, 전력부하 예측, 태양광 예측, 기업 부도 예측, 수면 온도 예측, 영상분류, 스팸메일 분류 등 광범위한 연구의 주요 방법론으로 사용되고 있다.
특히 본 연구와 마찬가지로 전력부하예측에서 최근 신경망 모형들이 많이 주목받고 있는 만큼 신경망 모형들의 활용 가능성을 파악하고 예측력을 비교해보는 것은 실증연구 측면에서 의미가 있다.
따라서 본 연구에서는 전력부하예측 중에서 주별 전력부하예측을 위해 LSTM 모형을 구축하여 활용하였다. 주별 전력부하예측의 경우 MTLF(Mid-Term Load Forecasting)에 속한다고 할 수 있다.
특히 LSTM 모형을 학습 방향에 따라서 단방향(Unidirectional) LSTM과 양방향(Bidirectional) LSTM으로 구분하고 은닉층의 수에 따라서 단층 LSTM과 Stacked LSTM으로 구분하여 연구를 진행하였다. 이는 전력부하를 예측하는 국내연구에서는 진행되지 않았던 부분인 만큼 본 연구의 큰 의의라고 할 수 있다. 뿐만 아니라 LSTM 모형의 예측력을 검증하고자 MLP 모형과의 예측력 비교도 실시하였다.
LSTM 모형의 입력변수로는 전력부하에 영향을 미치는 요인들을 반영하였다. 일반적으로 전력부하에 영향을 미치는 요인에는 날짜요인과 기상요인 그리고 경제요인 등이 있다.
본 연구에서 구축한 모형에서는 데이터의 빈도(Frequency)가 시간대별이라는 점에서 날짜요인과 기상요인을 반영하였다. 경제요인의 경우 최고빈도 자료가 일반적으로 월별자료이기 때문에 시간대별로 변환하기 위해서는 선형보간을 해야 하지만 경제요인이 시간대별로 변화한다고 합리적으로 보기 어렵기 때문에 제외하였다.
본 연구의 구성은 다음과 같다. Ⅱ장은 국내외 선행연구 및 본 연구의 차별점으로 LSTM 모형을 활용하거나 MLP 모형을 바탕으로 전력부하를 예측한 논문을 소개하였다. 이외에도 전력부하가 아니더라도 예측에 LSTM이나 MLP 모형이 활용된 연구도 추가로 정리하였다. 이처럼 다양한 국내외 연구를 살펴보며 선행연구들과 본 연구의 차별점을 제시하였다.
Ⅲ장은 본 연구에서 사용한 데이터셋을 소개하고 MLP와 LSTM의 방법론을 소개하였고, Ⅳ장은 본 연구에서 구축한 LSTM 모형 및 벤치마크 모형인 MLP모형을 소개하였다. 또한 모형별 비교를 위해 사용될 예측력 평가방법인 MAPE를 소개하고 이를 바탕으로 표본외 예측결과(Out of sample forecast)를 서술하였다.
Ⅴ장은 본 연구의 결론으로 LSTM 모형을 통한 주별 전력부하예측 결과를 바탕으로 본 연구의 의의와 향후 연구과제 등을 서술하였다.
Ⅱ. 선행 연구 및 본 연구의 차별점
2.1 국내 및 국외 선행연구
Kim[1]등은 하절기 평일의 전력수요 예측을 위해 인공신경망 모형을 활용하였다. 해당 연구에서 구축한 신경망은 입력층과 출력층 사이에 은닉층이 존재하는 MLP 모형이다. 은닉층은 1개로 구성하였으며 입력변수로는 하루의 전력수요가 가지는 주기성을 반영하고자 시간 인덱스를 추가하였으며 2일 전과 3일 전 전력시차항 그리고 기온변수를 함께 반영하였다. 다만 기상요인으로 기온만 반영되었다는 점과 다양한 날짜요인이 반영되지 않은 점은 해당 연구의 한계로 보인다.
Nam[2]등은 빅데이터를 활용하여 하절기 평일의 시간대별 전력수요를 예측하였다. 예측방법론으로는 MLP를 활용하였다. MLP 모형은 사용한 활성화함수(ELU 또는 ReLU)에 따라서 두 가지 모형으로 구분하였다. MLP 모형의 입력변수로는 전력시차항 이외에도 기온, 습도, 일사량, 일조량 등 다양한 기상요인을 반영하였으며 월, 일, 요일, 시간 등의 날짜요인을 더미변수 형태로 반영하여 전력부하에 영향을 미칠 수 있는 다양한 요인을 반영하였다. 특징적인 부분은 교통량 데이터도 활용했다는 점이다.
Muzaffar[3]등은 단기 전력부하 예측을 위해 LSTM을 활용하였다. 특히 LSTM 모형의 예측력을 검증하기 위해서 시계열 모형인 ARMA, ARIMA, SARIMA 모형과 예측력을 비교하였다. 예측기간은 향후 1일과 2일 그리고 7일과 30일로 총 4가지의 예측기간으로 구분하였다. 그 결과, 단기인 1일과 2일에는 LSTM 모형이 시계열 모형들에 비해서 예측력이 매우 우수한 것으로 나타났다. 다만, 7일과 30일에서는 시계열 모형들의 예측력이 LSTM에 비해서 예측성과가 뛰어난 것으로 나타났다.
Abbasimehr[4]등은 가구회사의 수요 데이터를 예측하기 위해서 LSTM을 활용하였다. 특히 단층이 아닌 다층구조를 사용하여 Stacked LSTM을 구축하였다. 구축된 Stacked LSTM을 다른 신경망 및 머신러닝 기법인 ANN과 SVM 등과 비교하였으며 전통적인 시계열 기법인 ARIMA와 ETS 모형과도 예측력을 비교하였다. 그 결과 SVM과 ANN보다 Stacked LSTM의 예측력이 더 뛰어난 것으로 나타났다. 또한 ARIMA 및 ETS와의 예측력을 비교한 결과도 Stacked LSTM이 더 좋은 예측성과를 나타냈다. 특히 주목할 부분은 SVM과 ANN도 전통적인 시계열 모형보다 좋은 예측력을 보여주어 전반적으로 인공지능을 활용한 방법이 실제 시계열 데이터의 패턴을 포착하는데 우수한 능력을 보여주는 것으로 나타났다.
Choi[5]등은 LSTM을 ResNet과 결합하여 STLF(Short Term Load Forecasting)에 활용하였다. 해당 결합모형은 ResNet의 산출값을 LSTM의 입력값으로 사용하는 모형이다. 예측 결과 해당 연구에서 제시한 ResNet/LSTM 결합 모형이 단일 모형인 MLP, ResNet 그리고 LSTM 보다 예측력이 높은 것으로 나타났다.
Atef[6]등은 전력부하예측을 위해 단방향(Unidirectional) Stacked LSTM과 양방향(Bidirectioanl) Stacked LSTM을 구축하여 예측력을 비교하였다. 먼저 단방향 단층 LSTM과 단방향 Stacked LSTM의 예측력을 비교한 결과 은닉층이 2개인 단방향 Stacked LSTM이 예측력이 가장 좋은 것으로 나타났다. 반면 양방향 단층 LSTM과 양방향 Stacked LSTM의 예측력을 비교한 결과 은닉층이 1개인 양방향 단층 LSTM의 예측력이 우수한 것으로 나타났다. 이를 바탕으로 최종모형을 단방향 Stacked LSTM과 양방향 단층 LSTM으로 각각 확정하였다. 최종모형들을 SVR 모형과 예측력을 비교한 결과, 양방향 단층 LSTM이 가장 우수했으며 그 다음으로 단방향 Stacked LSTM과 SVR 순으로 나타났다.
Kim[7]등은 단기 전력수요 예측을 위해서 LSTM 모형을 구축하였으며 입출력 값에 기존의 실수값이나 정규화된 값이 아닌 자연어 처리에서 많이 사용되는 원-핫 인코딩 기법을 활용하였다. LSTM 모형의 예측력 비교를 위하여 DNN 모형을 함께 구축하였는데 그 결과 원-핫 인코딩 기법을 적용한 LSTM모형이 기존의 LSTM 모형과 DNN 모형보다 더 좋은 예측력을 보여주었다.
Joo[8]등은 양방향 LSTM과 단방향 LSTM 모형을 구축하여 주가를 예측하는데 활용하였다. 그 결과 양방향 LSTM이 단방향 LSTM보다 더 예측성과가 좋은 것으로 나타났다.
Jo[9]등은 전력수요 예측을 위해 LSTM 모형을 활용하였다. 특히 해당 연구에서는 Attention Mechanism이라는 방법을 활용하여 출력값에 영향을 미치는 입력값의 열의 위치에 집중하여 학습할 수 있도록 하는 방법으로 실제로 예측결과에 영향을 미치는 소수의 입력값을 집중적으로 학습하도록 하였다. 그 결과, 기존의 LSTM 모형과 시계열 모형인 ARIMA에 비해서 MA(Modified Attention)-LSTM 모형이 더 뛰어난 예측성능을 보여주는 것으로 나타났다.
Cui[10]등은 교통량 데이터를 예측하기 위해서 단방향 심층 LSTM과 양방향 심층 LSTM을 구축하였다. 그 결과, 양방향 심층 LSTM 모형이 더 우수한 예측력을 보여주었다.
Poudel[11]등은 신경망 모형을 활용하여 태양광 발전 출력을 예측하였다. 이를 위해 MNN(Multilayer Neural Network)과 LSTM 모형을 활용하였다. 예측결과 MSE 측면에서 LSTM이 MNN 모형보다 예측력이 뛰어난 것으로 나타났으며 LSTM이 태양광 발전 출력 데이터의 갑작스러운 변동에 MNN에 비해서 덜 민감한 것으로 나타났다.
2.2 본 연구의 차별점
국내외 선행연구와 본 연구의 주요한 차별점은 다음과 같다. 먼저 현재 국내 연구 중에서 LSTM 모형을 활용하여 전력부하를 예측한 연구들 중 전력부하에 미치는 요인들을 다양하게 반영한 연구는 없다. 본 연구에서는 기상요인으로 기온, 습도, 일사량, 일조량, 강수량, 풍속 등을 반영하였다. 특히 기온의 경우 기온시차항과 기온제곱항을 추가하였다. 이는 기상요인 중 기온이 전력부하에 미치는 효과가 가장 큰 것으로 알려져 있기 때문이다.
또한 날짜요인으로는 월, 일, 요일, 시간에 대한 정보를 반영하고자 더미변수 형태로 반영하였고 전력시차항(3일전, 7일전)도 입력값으로 사용하였다.
LSTM 모형 측면에서는 단방향 LSTM과 양방향 LSTM으로 구분하여 전력부하를 예측했다는 점에서 그 의미가 클 것으로 기대한다.
단방향 LSTM과 달리 양방향 LSTM은 순방향과 역방향으로 각각 학습이 진행된 후 합쳐지는 만큼 기존의 단방향 LSTM에 비해서 예측력을 개선시킬 수 있는 방법으로 기대된다. 뿐만 아니라 LSTM을 단층과 Stacked로 구분하였다는 점도 본 연구의 큰 의의라고 할 수 있다. 이처럼 본 연구는 다양한 LSTM모형을 구축하여 전력부하 예측에 대한 활용가능성을 검토하는 실용적인 연구이다.
또한 본 연구에서 구축한 LSTM 모형의 예측력을 검증하고자 MLP 모형과의 예측력 비교도 함께 실시한만큼 다양한 신경망 모형을 활용하여 주별 전력부하를 예측할 수 있다는 가능성을 제시하는 연구가 될 것으로 기대한다.
Ⅲ. 데이터셋 및 분석 방법론
3.1 데이터셋
표 1은 본 연구에서 활용한 데이터셋이다. 전력 및 기상 데이터는 한국전력거래소(KPX)에서 제공받은 데이터를 활용하였으며 날짜요인과 관련된 데이터는 본 연구자가 직접 구축하였다. 데이터의 기간은 2000년에서 2019년으로 총 20년치의 데이터를 구축하였으며 데이터의 빈도는 모두 시간대별 자료이다.
3.2 분석 방법론
LSTM은 RNN이 가지고 있던 장기의존성 문제(Long-term dependency)를 해결하고자 나온 모형이다.
장기의존성 문제란 기존 RNN의 경우 학습 과정에서 기울기 소실 문제(Vanishing gradient problem)가 발생하며 아주 오래된 정보의 기억은 잃어버리게 되는 현상을 말한다. 즉 장기의존성 문제로 인해서 과거의 중요한 정보가 사라질 수 있기 때문에 해당 정보가 전력부하 예측에 반드시 필요한 정보였다면 예측력을 떨어트리는 요인으로 작용할 가능성이 높다.
이러한 RNN의 단점을 보완하여 LSTM은 직전 정보 뿐만 아니라 오래된 과거 데이터까지 고려하여 미래를 예측한다는 점에서 장기 시계열을 분석함에 있어서 큰 장점을 가진다. 따라서 최근 전력부하를 예측하는 연구에서도 MLP 모형과 함께 가장 많이 활용되고 있다.
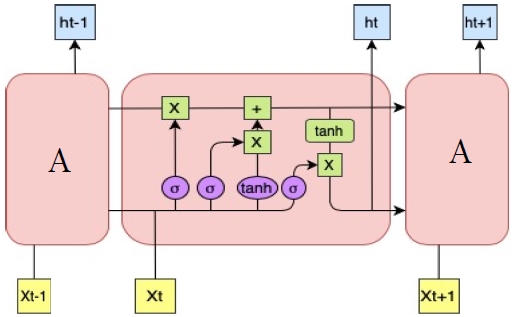
또한 LSTM의 메모리 셀에는 RNN에는 존재하지 않는 3개의 gate(forget gate, input gate, output gate)가 존재한다. 이 3개의 gate가 장기정보에 대해서 특정 정보는 잊어버리고 몇 가지의 정보는 추가하도록 조정하는 역할을 하여서 학습과정에서 기울기 소실 문제로 인해 장기의존성 문제가 발생하는 것을 방지한다. LSTM의 구조는 그림 1 및 아래 식 (1) ~ 식 (6)과 같다.
| (1) |
여기서 ft= forget gate, Wf= 가중치, ht-1=이전 단기 정보, xt=현재 정보, bf=편향, σ=시그모이드이다.
| (2) |
| (3) |
여기서 it= input gate, =업데이트할 정보 후보군, Wi,Wc= 가중치, ht-1=이전 단기 정보, xt=현재 정보, bi,bc=편향, σ=시그모이드, tanh=하이퍼볼릭탄젠트이다.
| (4) |
여기서 Ct= 업데이트 된 장기정보, ft= forget gate, Ct-1=이전 장기 정보, it=input gate, = 업데이트할 정보 후보군이다.
| (5) |
여기서 ot= output gate, σ=시그모이드, Wo= 가중치, ht-1=이전 단기정보, xt=현재 정보, b0=편향이다.
| (6) |
여기서 ht=현재 단기 정보, ot= output gate, Ct=업데이트 된 장기정보, tanh=하이퍼볼릭탄젠트이다.
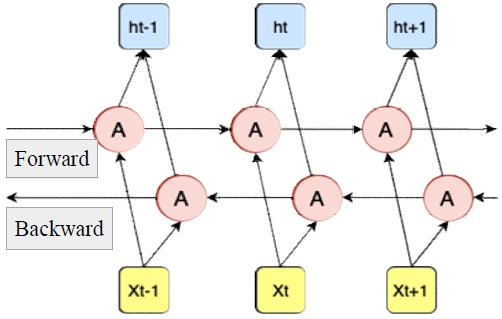
또한 LSTM 모형은 다양하게 구분될 수 있다. 특히 본 연구에서는 단방향 LSTM과 양방향 LSTM 모형으로 구분하여 구축한다. 그림 2에서 볼 수 있는 것처럼 일반적으로 순방향만 있는 경우를 단방향이라고 한다. 순방향이란 sequential data에서 처음에서 끝으로 가면서 학습을 하는 일반적인 학습방법을 의미한다. 반면 역방향이란 끝에서 처음으로 학습을 하는 것을 의미한다. 따라서 순방향과 역방향으로 각각 학습을 한 후 합쳐진 모형을 양방향 LSTM이라고 부른다.
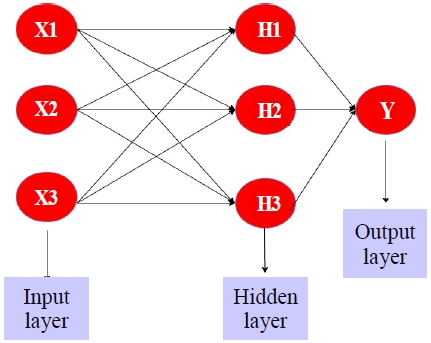
LSTM 모형의 예측력을 평가하기 위해 벤치마크 용으로 활용되는 것은 MLP 모형이다. 가장 기본적인 MLP모형의 구조는 그림 3과 같다.
MLP 모형은 입력층(Input layer)과 출력층(Output layer) 사이에 은닉층(Hidden layer)이 존재하는 신경망 모형으로서 은닉층의 개수가 2개 이상인 경우 DNN(Deep Neural Network)이라고 한다. MLP 모형의 경우 일반적으로 예측과 분류 문제를 해결하는 연구에서 광범위하게 활용되고 있다.
Ⅳ. 모형 구축 및 표본외 예측결과
4.1 예측모형 구축 및 예측력 평가방법
LSTM은 단층인지 심층인지 또는 단방향인지 양방향인지에 따라서 구분하여 모형을 구축하였다. 따라서 총 4가지의 모형을 구축하였으며 각 모형의 주요 특징은 표 2와 같다.
MLP 모형은 LSTM 모형들의 예측력을 비교하기 위한 벤치마크 모형으로 활용하였다. MLP 모형의 주요 특징은 표 3과 같다.
본 연구에서 구축한 모형들의 예측력을 서로 비교하고 평가하기 위해서는 객관적인 예측력 평가방법을 정해야 한다. 이를 위해서 MAPE(평균절대백분위오차)를 사용하였다. MAPE는 다음과 같다.
| (7) |
여기서 = 실제치, = 예측치이다.
4.2 표본외 예측기간 및 예측결과
표본외 예측기간은 2018년과 2019년의 하절기와 동절기를 선정하였다. 즉 2018년 1월과 8월 그리고 2019년 1월과 8월에 대해서 각각 주별로 예측을 실시하였다. 이는 주별 전력부하 예측에 있어서 하절기와 동절기의 예측력이 특히 중요한 만큼 본 연구에서 구축한 모형들의 예측력 평가 및 실제 향후 전력부하 예측에 활용될 가능성이 있는지를 검토하기 위함이다.
특히 대부분의 최대전력부하가 동절기와 하절기에 집중되고 8월과 1월에 최대전력부하가 발생하는 경우가 많기 때문에 본 연구에서 구축한 LSTM 모형이 실제 주별예측에 활용될 수 있는지를 검토하고자 해당 기간을 예측기간으로 설정하였다. 학습기간은 예측기간 전 3년으로 하였으며 입력값은 모형마다 모두 동일하게 적용하였다. 전력시차항으로는 3일전과 7일전 전력부하를 사용하였다.
기상요인으로는 기온, 기온시차항, 기온제곱항, 습도, 일사량, 일조량, 풍속, 강수량이 반영되었으며 날짜요인으로는 월, 일, 요일, 시간 더미가 반영되었다. 여기서 기상요인들은 모두 8대 도시의 인구가중치가 적용된 전국기상변수를 활용하였다. 기온시차항의 경우 1시간 전 시차항을 사용하였고 기온제곱항의 경우 전력과 기온 간의 비선형성을 반영하고자 전국기온의 quadratic(squared) term 형태로 구축하였다. 월, 일, 요일, 시간의 더미변수의 경우 해당 월, 일, 요일, 시간에 속한 경우 1을 입력하고 아닌 경우 0을 입력하는 형태의 더미변수로 구축하였다. 이외에 추세를 반영하기 위해서 연도더미도 추가하였다.
데이터 전처리를 위해서 scaler는 MinMax 방식을 사용하였다. 최적화기법으로는 Adam optimizer를 사용하였으며 학습률은 0.001을 적용하였다. 학습횟수의 경우 과대적합을 피하기 위해서 학습 조기종료(Early stopping)를 적용하여 training이 시작된 이후 MAPE의 개선이 없는 경우가 나타나면 학습을 중단하도록 설정하였다. 즉, MAPE 값이 이전 epoch에 비해서 높게 나오는 경우가 발생하면 중단하도록 설정하였다.
표본외 예측결과는 표 4와 표 5에 나타나 있는데 먼저 2018년에 대한 예측결과인 표 4를 살펴보면 2018년 1월과 8월의 주별예측에서 가장 좋은 예측성과를 나타낸 것은 ST-BLSTM인 것으로 나타났다. 평균적으로 MAPE 값이 3.80%인 것으로 나타나 가장 낮은 오차율을 보여주었다. 다만 주별로 세부적으로 살펴보면 가장 낮은 MAPE를 기록한 모형들이 상이하게 나타났지만 평균적인 수준을 볼 때 양방향 Stacked LSTM인 ST-BLSTM이 가장 뛰어난 결과를 보여주었다. 이는 2019년 결과인 표 5에서도 마찬가지로 나타났다.
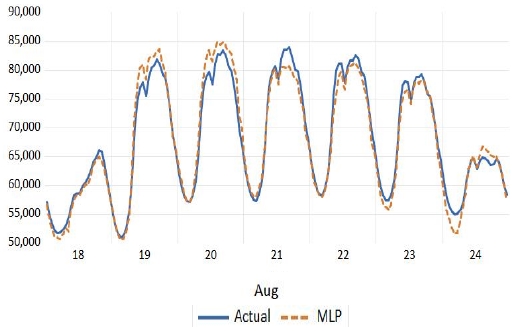
그림 4 ~ 그림 5는 각각 2018년 1월과 2018년 8월의 주차들 중 가장 낮은 MAPE를 기록한 모형의 예측치 및 실제치의 패턴이다. 마찬가지로 그림 6 ~ 그림 7은 각각 2019년 1월과 2019년 8월의 주차들 중 가장 낮은 MAPE를 기록한 모형의 예측치 및 실제치 패턴을 나타내고 있다.
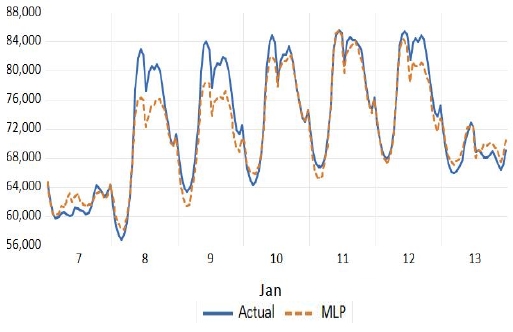
Hourly load patterns of predictive value and actual value. (18Y, MLP) (solid line = actual value, dashed line = predictive value)
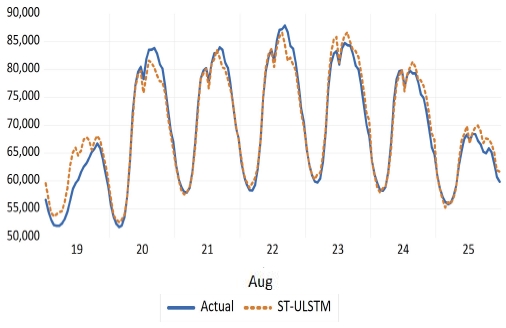
Hourly load patterns of predictive value and actual value. (18Y, ST-ULSTM) (solid line = actual value, dashed line = predictive value)
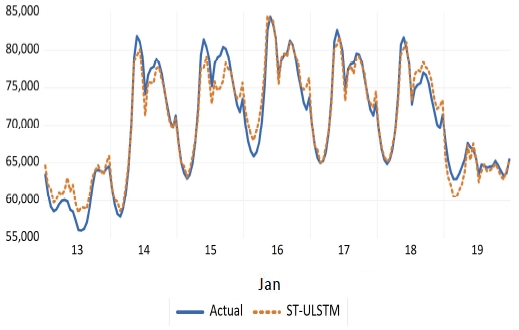
Hourly load patterns of predictive value and actual value. (19Y, ST-ULSTM) (solid line = actual value, dashed line = predictive value)
Ⅴ. 결 론
본 연구에서는 주별 전력부하를 예측하기 위해서 LSTM 모형을 구축하였다. 특히 본 논문의 주요한 공헌점으로 LSTM모형을 단방향(Unidirectional)인지 양방향(Bidirectional)인지 또는 단층(Single-layer)인지 심층(Stacked)인지에 따라 모형을 세분화하여 예측력을 비교하였다. 예측기간은 주별 예측에서 가장 중요한 시기인 동절기와 하절기를 택했으며 이에 따라 2018년 1월과 8월 그리고 2019년 1월과 8월을 선정하였다. 구축된 LSTM 모형들의 벤치마크 모형으로는 MLP 모형을 구축하여 예측력을 비교 및 검증하였다.
표본외 예측결과 ST-BLSTM(심층 양방향 LSTM)이 2018년과 2019년에 평균적으로 가장 낮은 MAPE를 기록하여 우수한 예측력을 보여주었다. 다만 각 주별로는 가장 좋은 예측력을 보여준 모형이 상이했지만 평균적인 수준을 고려할 때 ST-BLSTM이 안정적인 예측성능을 나타내었다. 또한 본 연구에서 구축한 4가지의 LSTM 모형이 모두 벤치마크 모형인 MLP 모형에 비해서 좋은 예측력을 나타낸 것을 볼 때 전력부하 예측에 있어서 LSTM 모형의 활용 가능성을 확인했다. 따라서 LSTM 모형들을 예측하고자 하는 전력부하의 특성에 맞게 더욱 세분화시킨다면 우수한 예측력을 나타낼 것으로 기대한다.
향후 연구에서는 예측분야를 확장하여 특수일 정보를 반영한 LSTM 모형을 구축하여 특수일 예측에 LSTM 모형을 활용할 필요가 있다.
References
-
K. H. Kim, R. J. Park, S. W. Jo, and K. B. Song, "24-Hour load forecasting algorithm using artificial neural network in summer weekdays", Journal of the Korean Institute of Illuminating and Electrical Installation Engineers, Vol. 31, No. 12, pp. 113-119, Dec. 2017.
[https://doi.org/10.5207/JIEIE.2017.31.12.113]

-
H. H. Jo, J. C. Kim, and Y. J. Nam, "Prediction of Special Day’s Hourly Load Using MLP, SVR and RF", The Journal of Korean Institute of Information Technology, Vol. 18, No. 5, pp. 1-11, May 2020.
[https://doi.org/10.14801/jkiit.2020.18.5.1]

-
S. Muzaffar and A. Afshari, "Short-term load forecasts using LSTM networks", Energy Procedia, Vol. 158, pp. 2922-2927. Feb. 2019.
[https://doi.org/10.1016/j.egypro.2019.01.952]

-
H. Abbasimehr, M. Shabani, and M. Yousefi, "An optimized model using LSTM network for demand forecasting", Computers & Industrial Engineering, Vol. 143, 106435, May 2020.
[https://doi.org/10.1016/j.cie.2020.106435]

-
H. Choi, S. Ryu, and H. Kim, "Short-term load forecasting based on ResNet and LSTM", In 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), IEEE, pp. 1-6, Oct. 2018.
[https://doi.org/10.1109/SmartGridComm.2018.8587554]

-
S. Atef and A. B. Eltawil, "Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting", Electric Power Systems Research, Vol. 187, 106489, Oct. 2020.
[https://doi.org/10.1016/j.epsr.2020.106489]

- K. H. Kim, B. Chang, and H. K. Choi, "Deep Learning Based Short-Term Electric Load Forecasting Models using One-Hot Encoding", Journal of IKEEE, Vol. 23, No. 3, pp. 852-857, Sep. 2019.
- I. T. Joo and S. H. Choi, "Stock prediction model based on bidirectional LSTM recurrent neural network", The Journal of Korea Institute of Information, Electronics, and Communication Technology, Vol. 11, No. 2, pp. 204-208, Apr. 2018.
-
Y. Jo and H. Lee, "Electricity Demand Forecasting Framework using Modified Attention-based LSTM", Journal of Korean Institute of Intelligent Systems, Vol. 30, No. 3, pp. 242-250, Jul. 2020.
[https://doi.org/10.5391/JKIIS.2020.30.3.242]

-
Z. Cui, R. Ke, Z. Pu, and Y. Wang, "Stacked Bidirectional and Unidirectional LSTM Recurrent Neural Network for Forecasting Network-wide Traffic State with Missing Values", arXiv preprint arXiv:2005.11627, , May 2020.
[https://doi.org/10.1016/j.trc.2020.102674]

-
P. Poudel and B. Jang, "Comparing Deep Learning Techniques for Modeling Photovoltaic Power Output", Journal of Advanced Information Technology and Convergence, Vol. 7, No. 2, pp. 43-54, Dec. 2017.
[https://doi.org/10.14801/jaitc.2017.7.2.43]


2018년 2월 : 한양대학교 경제학부(경제학 학사)
2020년 2월 : 연세대학교 경제학부(경제학 석사)
2020년 3월 ~ 현재 : 연세대학교 경제학부(경제학 박사과정)
관심분야 : 전력예측, 딥러닝, 머신러닝, 빅데이터, 인공지능

1979년 2월 : 연세대학교 경제학부(경제학 학사)
1981년 2월 : 연세대학교 경제학부(경제학 석사)
1987년 2월 : 시카고 대학교 경제학(경제학 박사)
1988년 ~ 현재 : 연세대학교 경제학부 교수
관심분야: 에너지경제학, 경기변동