4입력 다수결게이트를 사용한 QCA 기반 CAM 셀 설계

Ⅰ. 서 론

양자점 셀룰러 오토마타(QCA, Quantum-dot Cellular Automata)는 현대의 회로기술인 CMOS를 대체할 차세대 디지털 회로설계 기술로서 CMOS에 비해 발열량, 전력소모, 그리고 회로크기 등의 이점으로 주목받고 있다. QCA 환경에서 정보를 저장하는 저장장치는 많은 연구들이 진행되어 왔다. QCA를 이용하여 RAM[1], 레지스터[2] 그리고 CAM(Content-Addressable Memory)[3]-[6] 등 여러 저장장치들이 제안되어 왔지만, 최근에는 RAM과 레지스터를 중심으로 연구가 진행되고 있다. CAM은 Lempel-ziv 압축과 네트워크 스위칭 등 특수한 작업에 매우 빠른 속도를 제공할 수 있어 중요한 회로이다[3]. 본 논문에서는 내부에 저장된 정보를 사용하여 탐색을 진행하는 QCA CAM 셀을 제안한다.

본 논문에서 제안하는 CAM 셀은 3입력 AND 게이트를 기반으로 동작한다. 기존의 3입력 AND 게이트는 5입력 다수결 게이트를 기반으로 설계되었다. 이러한 구조는 연산을 수행하고자 하는 3개의 입력 외에도 2개의 입력이 더 필요하며, 이는 회로 구성 시 배선을 복잡하게 만든다. 따라서 배선의 복잡도를 줄이기 위하여 새로운 형태의 3입력 AND/OR 게이트를 제안하며, 이를 이용하여 CAM 셀을 설계한다. 제안하는 구조는 회로의 집적도를 향상시키기 위해 다층구조를 이용하여 설계한다.

Ⅱ. 관련 연구

2.1 QCA 기본 배경

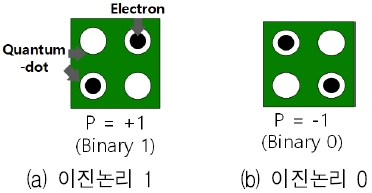
QCA는 양자 셀을 기본으로 회로를 구성한다. 각 양자 셀은 두 개의 전자를 가지며, 두 전자는 전자 간 밀어내는 힘인 쿨롱 반발력에 의해 서로 대각 방향으로 배치된다[7]. 이 때 전자들은 그림 1의 (a)와 (b) 둘 중 하나와 같은 형태를 띤다. 이러한 상태를 각각 +1과 –1의 편극상태라고 하며 이진논리의 1과 0에 대응한다. 양자 셀을 인접하게 배치하여 회로를 구성할 수 있으며, 특정 셀의 편극이 정해진다면, 쿨롱반발력에 의해 인접한 셀들의 편극 상태가 결정되며 신호가 전달된다.

Fig. 1.

Two polarization states of the basic QCA cell, (a) Binary logic 1, (b) Binary logic 0

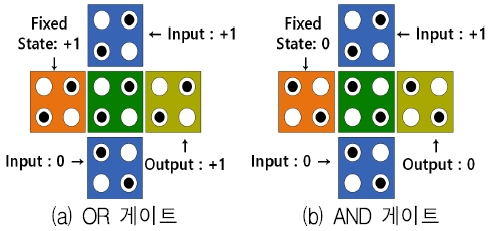
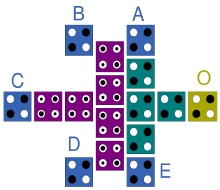
QCA 환경에서는 다수결 게이트를 사용하여 OR 연산과 AND 연산을 구현한다. 그림 2는 3개의 입력을 받는 3입력 다수결 게이트이다. QCA 회로에서 파란색 셀은 입력신호가 들어오는 셀이며, 노란색 셀은 신호가 출력되는 출력 셀이다. 또한 주황색 셀은 셀의 편극이 고정된 고정 셀이다. (a), (b)와 같이, 각각 한 개의 입력을 1과 0으로 고정시켜 2입력 OR 게이트와 AND 게이트를 구현한다[8].

Fig. 2.

3-input majority gate, (a) OR gate, (b) AND gate

2.2 QCA 상의 클럭

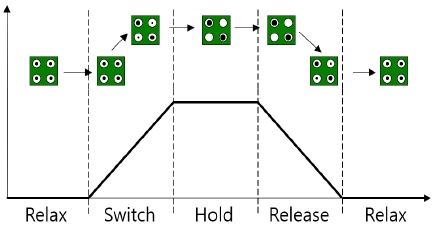
QCA 셀은 4단계의 클럭 상태를 가지며 그림 3에 표현되어 있다. 클럭은 셀의 전위가 점점 올라가 안정화 되는 과정인 천이(Switch), 양자 점간 전위가 안정화 된 유지(Hold), 전위가 점점 작아지고 편극이 사라져 가는 해제(Release), 그리고 편극이 사라진 휴지(Relax) 등 4가지의 상태로 구성된다.

Fig. 3.

Clock status

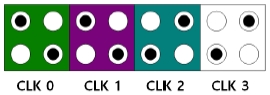
QCA에서는 그림 4와 같이 셀들을 클럭0(CLK 0), 클럭1(CLK 1), 클럭2(CLK 2), 그리고 클럭3(CLK 3)과 같이 네 클럭으로 구분하여 사용하며, 각 클럭은 이전 클럭보다 90°만큼 위상 지연을 가지고 있다. 예를 들어, 클럭0이 천이상태라고 하면, 클럭1은 유지 상태, 클럭2는 해제 상태, 그리고 클럭3은 휴지상태를 나타내게 된다[9][10].

Fig. 4.

Cell clock

셀에서 신호는 클럭 0에서 클럭3까지 그리고 클럭3에서는 다시 클럭0으로 신호가 순차적으로 전달된다. 한 클럭 간 신호가 전달과정에서, 신호의 약화가 발생하며 약화된 신호는 동일 클럭의 셀 하나를 거치며 다시 안정화된다.

2.3 기존의 QCA 3입력 AND/OR 게이트

QCA 환경에서 기존에는 3입력 AND/OR 게이트를 구현하기 위해 기존에는 5입력 다수결 게이트를 사용하였다. 5입력 다수결 게이트의 입력 중 2개의 입력을 0으로 고정시켜 3입력 AND 게이트를 구현하고, 반대로 1로 고정시킨다면 3입력 OR 게이트를 구현할 수 있다.

그림 5는 기존의 5입력 다수결 게이트를 보여준다. 이 회로는 면적이 크며 지연시간이 긴 단점이 존재한다[11].

Fig. 5.

Proposed 5-input majority gate in [10]

2.4 기존의 CAM 셀

CAM은 주소를 이용하여 정보를 탐색하는 RAM 과 달리, 내부에 저장된 정보를 이용하여 탐색을 진행하는 저장장치이다. CAM 구조는 정보를 저장하는 기억부(Memory unit)와 탐색하고자 하는 정보와 일치하는지 판단하는 판단부(Match unit)로 구성된다.

QCA 환경에서 CAM 셀을 설계하기 위해 그림 6에 표현되어 있는 루프 기반의 기억부가 사용되었으며 [3]-[6], 판단부를 구현하기 위해 3입력 게이트 [3], 5입력 소수결 게이트 [4]와 5입력 다수결 게이트 [5]를 사용되었다. 회로의 크기를 줄이기 위하여 다층구조를 이용한 회로가 제안되었으며 기존의 회로보다 면적이 크게 단축되었다[6].

Fig. 6.

Loop-based memory unit

Ⅲ. 4입력 다수결 게이트 설계

QCA 환경에서 기존의 회로들은 3입력 AND 게이트나 OR 게이트를 사용하기 위해 5입력 다수결 게이트를 이용한다. 하지만 이러한 구조는 연산을 수행하고자 하는 3개의 입력 외에 2개의 추가 입력이 필요하며, 이로 인해 회로를 확장할 때 배선의 배치가 복잡해 질 수 있다.

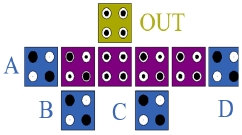
본 논문에서는 회로의 배선을 단순화하기 위해 필요 입력이 4개로 구성되며 3입력 AND/OR 게이트로 사용이 가능한 4입력 다수결 게이트를 제안한다. 제안하는 게이트는 그림 7에 나타나있으며, 셀 간 상호작용을 통해 회로가 동작한다.

Fig. 7.

Proposed 4-input majority gate

이 회로는 입력은 클럭0, 그 외 나머지 부분은 클럭1로 구성되고, 클럭0에서 클럭1로 신호가 전파되며, 클럭 1에서 클럭 0으로 신호는 역으로 전파되지 않는다. 입력 셀 A의 전자들이 거리가 가장 가까워 신호 전파 속도가 빠르기 때문에 2의 가중치를 가지며, 그 외의 B, C와 D는 1의 가중치를 가진다. 이 회로는 입력 신호가 1인 가중치의 합이 3 이상일 때, 1을 출력한다. 따라서 A의 입력이 0일 때, 다른 세 입력이 모두 1일 때만 가중치의 합이 3이상이 되기 때문에 1을 출력하며, A가 1일 때는 다른 세 입력 중 하나의 입력만 1이라도 1을 출력한다. 이는 A가 0일 때는 세 입력 B, C와 D를 AND연산 한 결과가 나오며, A가 1일 때는 OR연산 한 결과가 출력된다.

Ⅳ. QCA CAM 셀 설계

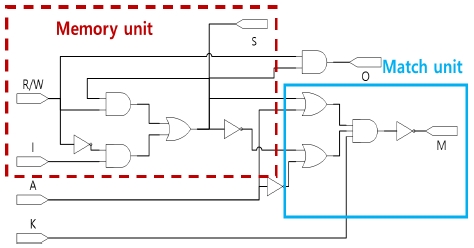
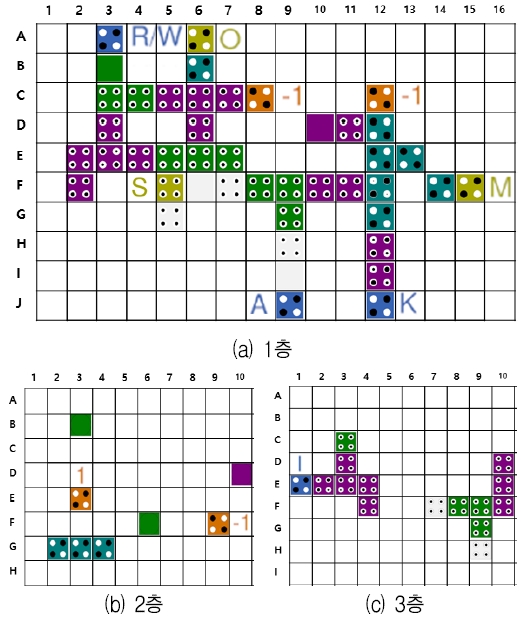
본 논문에서는 제안한 4입력 다수결 게이트를 사용하여 배선의 복잡도를 줄이고 다층구조를 기반으로 설계하여 회로의 필요 면적을 감소시킨 회로를 제안한다. 그림 8은 본 논문에서 제안하는 QCA CAM 셀의 논리도이다. 점선으로 된 박스는 정보를 저장하는 기억부이며, 실선 박스는 판단부의 논리도이다. 그림 8을 바탕으로 그림 9의 QCA CAM 셀을 설계하였다. 제안된 회로는 3층 구조를 가지며, [6]에서 사용한 다층구조 기억부를 이용한다. 또한 그림 7의 4입력 다수결게이트를 사용하여 회로를 구성하였다.

Fig. 8.

Logic diagram of proposed CAM cell

Fig. 9.

Proposed QCA CAM cell, (a) Layer 1, (b) Layer 2, (c) Layer 3

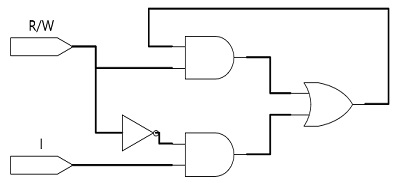
그림 9(a)의 F행 5열의 출력 S는 기억부에 저장된 정보이며, 입력 R/W는 기억부의 읽기, 쓰기 동작을 결정한다. 표 1에 기억부의 진리표가 표기되어있으며, 기존에 저장되어 있던 값을 S(t-1)로, 입력에 의해 새로 저장되는 값을 S(t)라고 표현한다.

Table 1.

Truth table of CAM cell’s memory unit

R/W=0일 때, 쓰기 동작이 수행되며, 입력 I의 값이 기억부에 저장되고, O는 0을 출력한다. 또한 R/W=1일 때, 읽기 동작을 수행한다. 이때, 기억부는 기존에 저장하고 있던 정보를 유지하며, 저장된 정보를 O를 통해 출력된다.

표 2는 CAM 셀의 판단부의 진리표이다. 출력 M이 1일 때, 탐색하는 정보와, 기억부에 저장된 정보가 일치하여 탐색이 성공적으로 수행됨을 의미한다. A는 탐색하고자 하는 정보이며, S는 기억부에 저장된 정보이다. K=0이면, S와 상관없이 M=1을 출력한다. K=1이면, 탐색 값 A와 저장된 정보인 S가 일치할 때만 M=1을 출력한다.

Table 2.

Truth table of CAM cell’s match unit

Ⅴ. 비교 및 분석

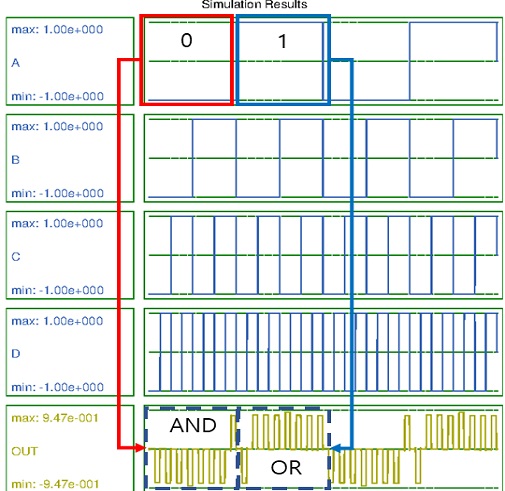
본 논문에서는 4입력 다수결 게이트를 설계하고, 이를 사용하여 CAM 셀을 설계하였다. 설계한 회로와 비교자료들은 QCADesigner를 이용하여 설계되었으며, 결합벡터 방식(Coherence vector)을 이용하여 시뮬레이션을 진행하였다. 그림 10은 제안된 4입력 다수결 게이트의 시뮬레이션 결과이며, A의 입력에 따라 나머지 입력 B, C, D의 3입력 AND/OR 연산을 정상적으로 수행하는 것을 볼 수 있다. 그림 5의 회로는 13,524nm²의 면적과 3단계의 클럭 사이클로 구성되어, 0.75 클럭사이클의 지연시간을 가지지만, 제안된 4입력 다수결 게이트는 6,844nm²의 면적과 2단계의 클럭 사이클로 구성되어 0.5 클럭사이클의 지연시간을 가져 면적과 동작속도에 이점이 있다.

Fig. 10.

Simulation result of proposed 4-input majority gate

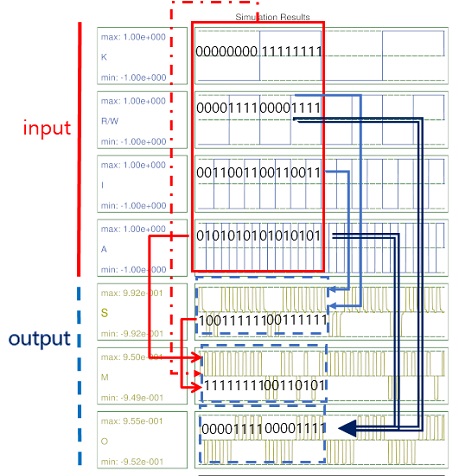
그림 11은 본 논문에서 제안된 CAM 셀의 시뮬레이션 결과이며, 정상적으로 동작하는 것을 확인할 수 있다. 표 3은 CAM 셀의 성능비교표이며, 이 표에서 비용은 식 (1)을 통하여 산출된 값이다[12].

Fig. 11.

Simulation result of proposed CAM cell

Table 3.

Performance table of CAM cell

본 논문에서 제안하는 CAM 셀은 필요 면적은 59,004nm², 필요 셀 수는 68개, 지연시간은 1.75 클럭사이클, 그리고 비용은 180,699.75의 성능을 나타낸다.

표 3을 참고하면, 제안하는 회로는 기존의 회로에 비해 필요면적이 축소되었을 뿐만 아니라, 모든 부분에서 성능이 향상됨을 확인 할 수 있다.

Ⅵ. 결 론

QCA 환경에서 3입력 AND/OR 동작을 구현하기 위해 기존에는 5입력 다수결 게이트를 사용한다. 이는 연산을 수행하려는 3개의 입력외의 2개의 추가입력이 필요하여 회로 배선의 혼잡을 야기한다. 본 논문에서는 이를 개선하기 위해 4개의 입력만으로 3입력 AND/OR 동작을 수행하는 4입력 다수결 게이트를 설계하고, 이를 기본소자로 하는 QCA CAM 셀을 제안하였다. 제안된 회로는 배선을 단순화시켰으며. 다층구조로 설계하여 필요면적이 축소되었다. 또한 회로의 지연시간 및 필요한 셀 수 등 다른 성능들 또한 개선되었다.

Acknowledgments

이 연구는 금오공과대학교 학술연구비로 지원되었음(과제번호: 202001880001).

References

• M. Abdullah-Al-Shafi, and A. N. Bahar, "A New Structure for Random Access Memory Using Quantum-Dot Cellular Automata.", Sensor Letters, Vol. 17, No. 8, pp. 595-600, Aug. 2019. [https://doi.org/10.1166/sl.2019.4117]
• J. C. Jeon, "Low Complexity QCA Universal Shift Register Design Using Multiplexer and D Flip-Flop Based on Electronic Correlations", The Journal of Supercomputing, Vol. 76, No. 8, pp. 6438-6452, Aug. 2019. [https://doi.org/10.1007/s11227-019-02962-y]
• LHB Sardinha, DS Silva, MAM Vieira, LFM Vieira, and O. P. V. Neto, "Tcam/cam-qca: (ternary) content addressable memory using quantum-dot cellular automata.", Microelectronics Journal, Vol. 46, No. 7, pp. 563-571, Jul. 2015. [https://doi.org/10.1016/j.mejo.2015.03.020]
• S. R. Heikalabad, A. H. Navin, and M. Hosseinzadeh, "Content addressable memory cell in quantum-dot cellular automata", Microelectronic Engineering, Vol. 163, pp. 140-150, Sep. 2016. [https://doi.org/10.1016/j.mee.2016.06.009]
• M. B. Khosroshahy, M. H. Moaiyeri, and K. Navi, "Design and evaluation of a 5-input majority gate-based content-addressable memory cell in quantum-dot cellular automata", 2017 19th International Symposium on Computer Architecture and Digital Systems, pp. 1-6, Dec. 2017. [https://doi.org/10.1109/CADS.2017.8310671]
• C. S. Park and J. C. Jeon, "Design of QCA Content-Addressable Memory Cell for Quantum Computer Environment", The Journal of the Convergence on Culture Technology, Vol. 6, No. 2, pp. 521-527, May 2020.
• N. Safoev and J. C. Jeon, "Design of high-performance QCA incrementer/decrementer circuit based on adder/subtractor methodology", Microprocessors and Microsystems, Vol. 72, p. 111197, Feb. 2020. [https://doi.org/10.1016/j.micpro.2019.102927]
• N. Safoev and J. C. Jeon, "A Novel Controllable Inverter and Adder/Subtractor in Quantum-Dot Cellular Automata Using Cell Interaction Based XOR Gate", Microelectronic Engineering, Vol. 222, p. 111197, Feb. 2020. [https://doi.org/10.1016/j.mee.2019.111197]
• J. C. Jeon, "Designing nanotechnology QCA–multiplexer using majority function‑based NAND for quantum computing", The Journal of Supercomputing, May 2020, Online published. [https://doi.org/10.1007/s11227-020-03341-8]
• N. Safoev and J. C. Jeon, "Design and Evaluation of Cell Interaction Based Vedic Multiplier Using Quantum-Dot Cellular Automata", Electronics, Vol. 9, No. 6, p. 1036, Jun. 2020. [https://doi.org/10.3390/electronics9061036]
• M. Balali, A. Rezai, H. Balali, F. Rabiei, and S. Emadi, "A novel design of 5-input majority gate in quantum-dot cellular automata technology". In 2017 IEEE Symposium on Computer Applications & Industrial Electronics, pp. 13-16, Apr. 2017. [https://doi.org/10.1109/ISCAIE.2017.8074941]
• C. D Thompson, "Area-time complexity for VLSI", In Proceedings of the eleventh annual ACM symposium on Theory of computing, pp. 81-88, Apr. 1997.