수치해석을 이용한 수평축 소형 다운윈드 풍력터빈의 출력에 관한 연구

Ⅰ. 서 론

태양으로부터 오는 복사열은 지구의 땅과 물의 불균등한 가열로 인해 바림이 발생되며, 지역 간 온도 차이가 공기 순환을 유도한다. 재생 가능 에너지의 원천인 바람은 우리 시대의 가장 시급한 문제 중 하나인 지속 가능한 삶을 위한 무공해 전기에 대하여 점점 더 실행 가능한 해결책으로 제시되고 있다[1][2].

풍부한 풍력 자원으로 인해 현재의 화석 연료 기반 에너지의 가장 실용적이며, 대체 에너지원으로 여겨지고 있다. 지구 온난화와 함께 화석 연료 가격의 지속적인 증가와 온실 가스의 대기 오염을 최소화하기 위해서 선진국의 많은 사람들이 신속하게 대응하게 되었다.

지난 20년 동안 상업용 수평축 풍력터빈(HAWT, Horizontal Axis Wind Turbine)의 공기역학적 설계기법에 대한 급속한 기술의 발전은 바람으로부터 훨씬 더 큰 운동 에너지를 추출 할 수 있는 능력을 크게 향상시켜 현재 상용 풍력터빈은 최대 6MW의 출력을 낼 수 있다. 상업용 풍력터빈과는 달리, 소규모의 수평축 풍력터빈은 낮은 효율과 공간적인 제약, 높은 자본 비용과 같은 여러 요인으로 인하여 상업용 풍력터빈과 같은 속도로 발전하지는 못하였다[3].

최근 들어 미국에서 소형 주거용 풍력터빈이 뉴욕 일부 지역에서 허용되는 등 국내 및 산업 건물에 소형 풍력터빈을 사용한 전기 생산에 대하여 관심이 증가하고 있다.

일반적으로 수직축 풍력터빈에 비하여 효율이 뛰어난 수평축 풍력터빈에는 블레이드가 타워의 전면부에 위치하여 회전면(Swept area)이 바람의 흐름에 직각이 되도록 방향 날개가 있는 업윈드(Upwind) 형식과 방향 날개를 대신하여 블레이드가 바람에 따라 자유롭게 요 제어가 가능하도록 타워의 후면부에 위치한 다운윈드(Downwind) 형식으로 나뉜다.

다운윈드 터빈은 Madsen 등의 연구에서 타워를 지난 와류와 블레이드가 충돌할 때 가장 높은 소음이 발생하여 타워 후류의 영향으로 블레이드의 소음과 진동의 원인이 되나[4], Choi 등은 타워 뒤에서 바람을 받아 블레이드의 휨에 의한 타워와의 충돌을 방지할 수 있어 최대 제한 풍속을 더 높일 수 있으며, 방향 날개가 불필요하므로 구조적으로 간단하여 설치 단가를 절감할 수 있는 장점을 설명하고 있다[5].

본 연구에서는 상용화를 위한 전 단계로 300W급 다운윈드 타입의 수평축 풍력터빈 개발을 위한 3차원 기본 형상 설계와 수치해석을 이용하여 실제 터빈에 유입되는 6~12㎧의 풍속 조건과 각각의 블레이드의 회전수에 대한 k-ε 난류 모델의 수렴 조건 분석에 의한 기계적 출력을 비교하여 풍력터빈의 성능을 예측하고자 한다.

Ⅱ. 풍력터빈 설계

2.1 블레이드 및 풍력터빈 설계

Verelst 등은 논문에서 연구되는 풍력터빈과 비슷한 크기의 300W급 다운윈드 자유 요 시스템의 실험적 연구를 진행하였으며, Larwood 등은 업윈드 형식에 비해서 다운윈드 형식은 타워 후류 효과로 인하여 블레이드의 피로 하중이 증가되는 단점을 확인하였다[6][7].

일반적인 수평축 풍력터빈은 업윈드 형식으로 풍압에 의한 블레이드의 파손을 방지하기 위하여 타워에서 일정 거리 떨어져 설계하며, 요 제어시스템을 장착하게 된다. Wang 등은 이러한 구조적 설계의 어려움으로 업윈드 형식의 단점을 보완한 다운윈드 형식을 제안하였다[8].

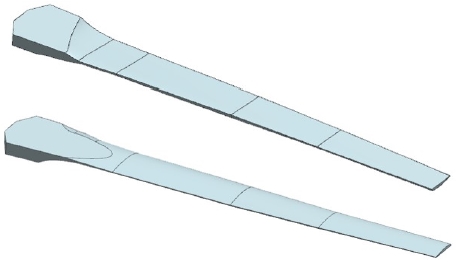
그림 1은 풍력터빈 개발을 위해 적용된 블레이드 상·하부 형상을 보여준다. Kim 등의 논문에서 실제 풍력터빈에 적용하기 위한 블레이드의 3차원 형상과 각각의 위치에 따른 에어포일 단면을 이용하여 블레이드의 전체 길이 750㎜, 로터 중심부 100㎜, 블레이드 끝단부 48㎜, 두께 25㎜로 상용 CAD 프로그램 NX 9.0을 이용하여 블레이드의 형상을 모델링 하였다[9]. 실제 풍력터빈에 사용되는 블레이드는 FRP 재질로 외형을 성형하고, 내부에는 강도를 보강하기 위하여 발포제를 이용하여 제작한다.

Fig. 1.

3D shape of blade

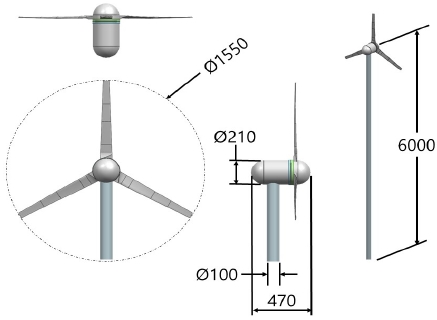
그림 2는 본 연구를 통하여 개발하기 위한 수평축 다운윈드 풍력터빈의 전체 모델링 형상을 보여준다. 풍력터빈의 기본 성능이라 할 수 있는 블레이드의 회전 직경은 1,550㎜이다. 풍력터빈을 설계하는 과정에서 나셀의 내부에 발전기를 배치하고, 발전기의 로터에 블레이드를 고정하고, 요 제어를 위한 시스템을 발전기에 장착하여 타워에 고정할 수 있는 나셀 공간을 확보하였다. 그림 2의 오른쪽 형상은 풍력터빈의 공력 해석을 위하여 타워의 높이를 블레이드 회전 직경의 약 4배 높이로 해석을 하였다. 블레이드 회전반경은 입구부를 기준으로 시계방향으로 회전되며, 풍력터빈이 조립되어 있는 타워의 직경은 100㎜이다.

Fig. 2.

3D shape of downwind horizontal axis wind turbine

2.2 수치해석 조건

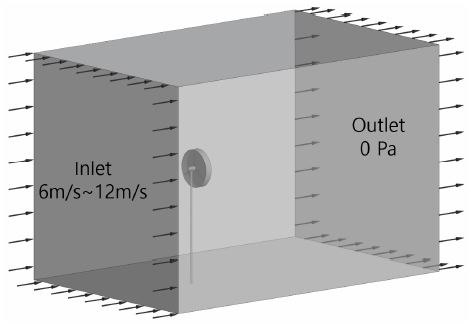
지난 연구에서 상용 소프트웨어인 ANSYS CFX 프로그램을 이용하여 유동장 풍속 10㎧에서 풍력터빈의 발전 성능을 동일한 격자 및 해석 조건에서 난류 모델을 해석 한 결과 토크와 출력이 k-ϵ > k-ω > SST 순으로 최대값을 확인할 수 있었다.[9] 본 연구에서는 해석상에서 최대값을 얻을 수 있는 k-epsilon 난류 모델을 사용하여 다양한 풍속에서 수치해석을 진행하였다. 인터페이스 경계 조건은 GGI(General Grid Interface) 옵션을 사용하여 유동 영역과 회전 영역에서의 해석 영역을 계산하였다. 입구 조건은 면을 기준으로 각각 6 ~ 12㎧의 조건에서 1㎧ 간격으로 수행하였다. 출구 조건은 평균 정압 기준으로 외부 영향이 없도록 0 Pa이며, 블레이드, 타워, 나셀과 바닥면은 벽면(Wall) 조건으로 수행하였다.

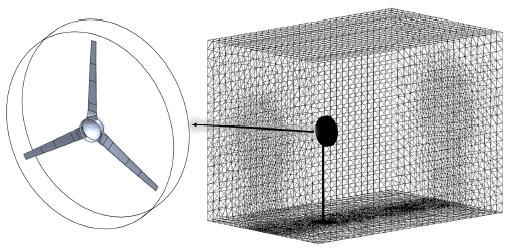
NX 9.0을 이용하여 설계된 모델링 형상을 상용 해석 프로그램인 ANSYS CFX를 통해 그림 3과 같이 두 개의 영역으로 구분하여 해석을 위한 격자를 구성하였다. 그림 3의 왼쪽 그림은 전체 해석 영역 중에서 회전되는 부위로 실린더 형상에서 내측의 블레이드를 제외한 공기 흐름 영역이다. 오른쪽 그림은 유동 영역에 대한 전체 경계 조건으로 그림 4의 블레이드 회전 영역을 제외한 직사각형 형상으로 구성하였다. 블레이드 회전 직경을 기준으로 입구 영역은 가로 8배, 세로 8배이다.

Fig. 3.

Mesh design of flow field

Fig. 4.

CFD boundary condition

입구 영역의 중앙에 터빈의 회전 중심을 위치하였고, 입구에서 출구까지의 전체 길이는 직경의 12배로 입구에서 4배가 되는 지점에 타워의 중심으로 해석하였다.

해석용 격자는 사면체로 구성되어 있으며 유동 영역은 약 4,500,000개와 회전 영역은 6,000,000개의 요소로 구성하였다. 유동 영역의 입구에서 출구까지 블레이드와 타워의 투영 부위는 다른 영역에 비해서 격자의 크기를 적게 하였으며, 유동 영역과 회전 영역에 대한 인터페이스 부분은 동일한 간격으로 설정하였다. 블레이드, 나셀, 타워는 유동 흐름에 있어 영향이 있는 부분으로 다른 격자에 비해 조밀하게 생성하였으며, y+ 값을 기준으로 규칙적으로 변화하여 유동 흐름의 변화가 많은 부위의 해석 결과를 높이도록 격자를 구성하였다. 그림 4는 수치해석에 사용한 경계 조건을 보여준다.

Ⅲ. 해석 결과

3.1 수치해석 결과

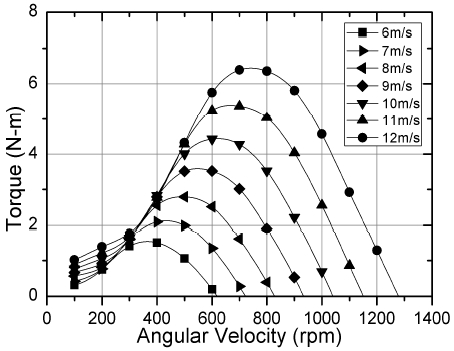
Kim은 입구에서 풍속 6 ~ 12㎧ 조건에서 블레이드 회전 속도별로 토크를 계산하였다[10]. 표 1은 수치해석에 의해서 계산된 토크 값을 입구에서의 풍속과 블레이드의 회전 속도를 구분하여 보여준다. 토크 값은 풍속별로 계산을 하였으며, 그림 5는 회전 속도에 따른 토크 값을 정리한 그래프로, 풍속에 따른 블레이드의 회전 속도가 전체적으로 비슷한 특성을 보인다. 낮은 회전 영역에서는 토크가 풍속에 따라 약간의 차이가 있으나, 회전 속도가 증가하는 경우에 점진적으로 증가하다가 특정 회전 속도에 이르면 토크 값이 감소되는 것을 확인할 수 있다.

Table 1.

Result of torque vs RPM by wind condition

Fig. 5.

Graph of torque vs RPM[10]

$\[ P\left(W\right)=T\cdot \omega =T\cdot \frac{2\pi N}{60} \]$

(1)

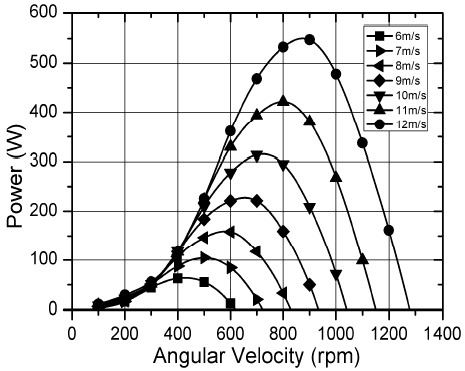
계산된 토크 값에 회전 속도를 곱하면 기계적인 출력값을 얻을 수 있다. 표 2는 회전 속도와 토크 값을 식 (1)을 적용하여 얻은 블레이드에서의 기계적인 출력값이며, 그림 6은 예상 출력을 그래프로 도시하였다.

Table 2.

Result of power vs RPM by wind condition

Fig. 6.

Graph of power vs RPM[10]

300rpm 이하의 낮은 회전수에서는 풍속과 무관하게 비슷한 출력값을 보이며, 6㎧에서는 400rpm 전후에서 최대 출력을 보이다가 로터의 회전이 증가하는 경우에는 출력값이 떨어지는 것을 확인할 수 있다.

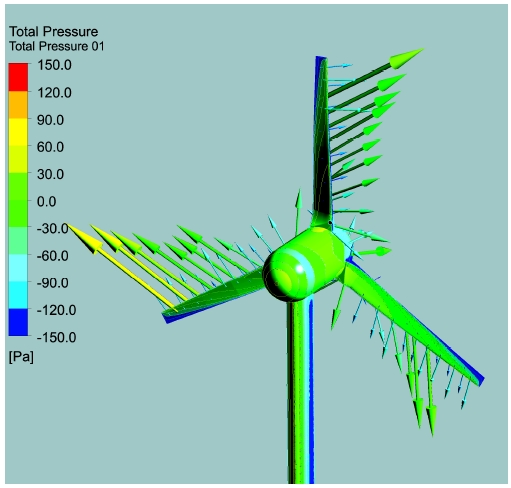
입구 조건에 따라 로터가 회전하면서 시스템 주위의 압력, 속도 등 수치해석 결과를 얻을 수 있다. 그림 7은 10㎧에서 타워와 로터에서 계산된 전압력을 색상별 표현하였으며, 동시에 로터 블레이드 단면에서의 속도를 벡터로 가시화하여 유동장의 형상을 확인하였다. 블레이드에 적용된 압력에 따라 연결된 발전기의 중심축에서 회전 토크 값을 계산 할 수 있다.

Fig. 7.

Contour of total pressure

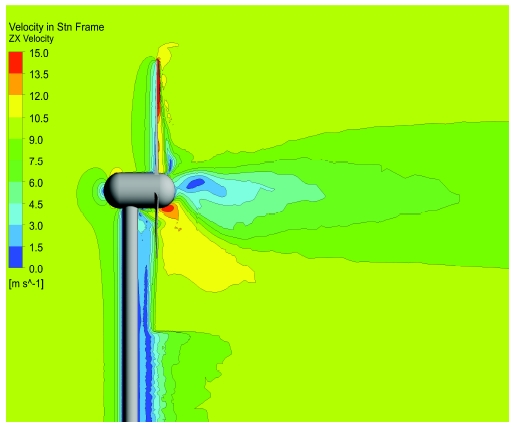
그림 8은 입구 조건이 10㎧에서 ZX 기준 단면에 대하여 타워와 로터 근처에서의 속도를 보여주고 있으며, 수평축 다운윈드의 형태로 인하여 흐름 방향에 따라 타워가 로터 앞쪽에 위치하여 간섭으로 인해 속도가 줄어들어드는 것을 확인할 수 있다.

Fig. 8.

Velocity in Stn frame

CFD는 어느 정도의 오차를 갖는 근사해를 갖는다. 반복 계산을 통하여 해석 결과값에 수렴하도록 하여 오차를 최소화한다. 양호한 목표 결과를 위하여 반복 횟수를 증가시키는 경우 결과는 더 좋을 수 있으나 계산에 의한 과도한 해석 시간이 소요되는 단점이 있다. 따라서 수치적인 오차를 최소한으로 하는 해석이 필요하다.

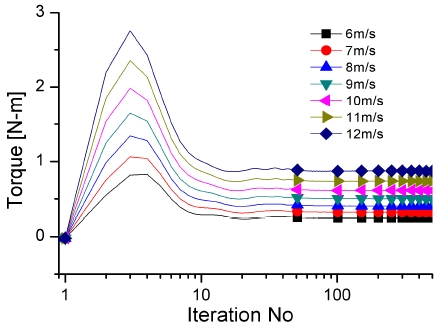
그림 9~12는 해석 조건에서 반복 횟수에 따라 풍력터빈에서의 토크 값을 보여주고 있다. 초기에는 결과값에 변동이 많으며 시간이 지나면서 안정된 결과를 확인할 수 있다. 반복 횟수 항목은 로그 스케일을 적용하여 도시하였다.

그림 9는 50rpm에서의 토크 값 변화이며, 100회 미만에서 전체적으로 값이 빠르게 수렴하는 것을 보여주고 있다. 블레이드의 회전 속도가 낮은 경우에는 토크 값이 수렴하는데 계산 횟수가 높은 RPM에 비해서 빠름을 알 수 있다.

Fig. 9.

Torque vs iteration by 50rpm

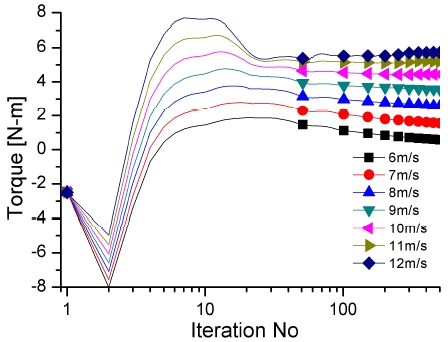
그림 10은 300rpm에서의 토크 값 변화를 나타내었으며, 50rpm에 비해 수렴이 쉽게 되지 않고 값의 변화가 많음을 알 수 있다.

Fig. 10.

Torque vs iteration by 600rpm

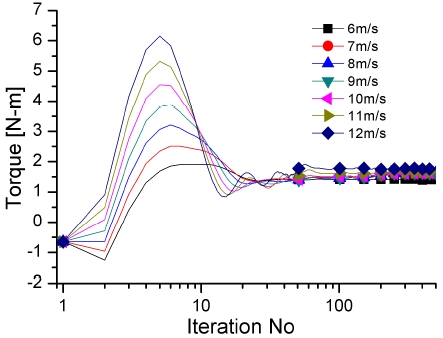
그림 11은 600rpm에서의 결과로 풍속이 낮은 경우에 토크 값에 대한 그래프의 기울기가 생기는 것을 알 수 있다. 그림 5와 같이 회전수에 따라 토크 값을 계산할 때 어느 시점이 지나면 음의 토크가 발생된다. 6㎧에서는 토크 값이 음의 값으로 떨어지기 직전에 해석상 불안정한 조건이 발생되는 것으로 추정되며 해석을 하는데 있어서 반복 횟수를 늘려 결과에 수렴할 수 있다. 블레이드의 회전 속도가 빠른 경우에는 토크 값 수렴을 위하여 많은 횟수의 계산 과정이 필요하다. 그림 5에서 회전 속도에 따른 최대 토크값이 변하게 된다.

Fig. 11.

Torque vs iteration by 300rpm

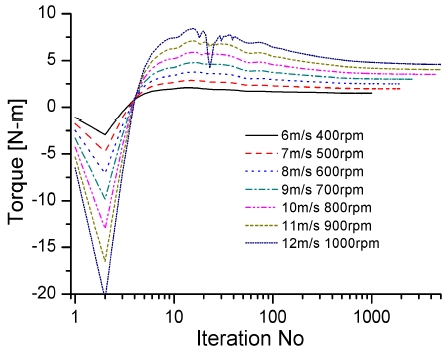
그림 12는 입구 풍속에 따른 블레이드의 회전 속도별 최대 토크값의 반복 횟수에 대한 수렴성을 나타내었다. 풍속 6㎧(400rpm), 7㎧(500rpm), 8㎧(600rpm), 9㎧(700rpm), 10㎧(800rpm), 11㎧(900rpm), 12㎧(1000rpm)로 토크 값이 최대값에서 감소가 된 상태에서 계산을 하였다. 전체적인 그래프의 경향은 풍속이 증가하면서 처음 시작할 때 토크에 대한 변동률이 크다는 것을 알 수 있으나 안정화 되어지는 과정은 비슷하게 나타나는 것을 확인할 수 있다. 회전수가 비슷한 경우에는 풍속에 따라 변동 폭은 차이가 있으나, 전체적인 경향이 비슷하게 진행되는 것을 알 수 있다.

Fig. 12.

Torque vs iteration by condition

수평축 풍력터빈의 형상 최적화를 위하여 중요한 요소 중 하나는 주속비(Tip speed ratio)이다[11]. 블레이드 끝단부 속도(V_tip)와 풍속(V_w)에 대한 비를 풍력터빈의 주속비(λ)라 하며 식 (2)와 같다.

$\[ TSR\left(\lambda \right)=\frac{V_{tip}}{V_w}=\frac{\left(2\pi N/60\right)R}{V_w} \]$

(2)

풍력터빈에서 얻을 수 있는 출력값 P, 공기 밀도 ρ인 경우 풍력에너지에 대한 비율을 출력 계수라 하고 식 (3)과 같다.

$\[ C_p=\frac{P}{\frac{1}{2}\rho V_w^3} \]$

(3)

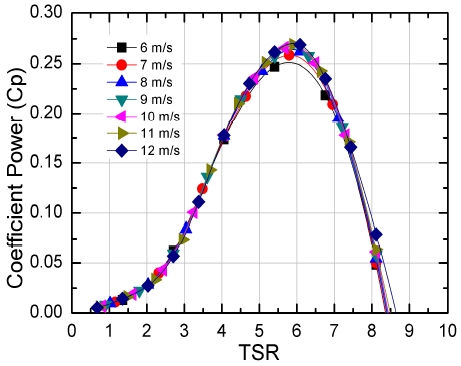
그림 13은 수치해석에 의해 얻은 계산 값에서 주속비를 반영한 출력 계수(Cp)를 나타내고 있다. 평균 TSR은 5.85로 고속형 블레이드 타입의 풍력터빈이다. 풍속과 상관없이 TSR과 Cp에 대한 관계는 비슷한 형태로 계산된다.

Fig. 13.

Coefficient of power(Cp) vs TSR

Ⅳ. 결 론

300W급 수평축 다운윈드 소형 풍력터빈을 개발하기 위한 3차원 형상 설계를 진행하였다. 3차원 설계를 통하여 개발 과정에서의 손실을 줄이고 풍력터빈의 성능을 높이기 위한 과정이다. 설계된 기본 형상을 이용하여 풍력터빈의 성능 예측을 위한 공력 해석을 진행하였다. 상용 소프트웨어 ANSYS CFX를 이용하여 각각의 풍속과 RPM 조건에서의 토크 값을 계산하고, 토크 값과 회전 조건에서의 블레이드 회전 속도로 기계적 출력을 예측하였다. 해석 결과 풍속 10㎧에서 300W급 성능의 공력 해석 결과를 확인하였으며, 해석을 하는 과정에서 토크 값에 대한 수렴 여부를 확인하여 조건별 계산 속도를 단축시킬 수 있음을 검토하였다. 설계된 풍력터빈은 TSR 5.85에서 Cp값 0.28이 됨을 확인하였고, 풍력터빈의 성능을 검증하여 개발 과정에서의 안정성을 확인하였다.

References

• B. Bavanish B. and K. Thyagarajan, "Optimization of power coefficient on a horizontal axis wind turbine using bem theory", Renewable and Sustainable Energy Reviews, Vol. 26, pp. 169-182, Oct. 2013. [https://doi.org/10.1016/j.rser.2013.05.009]
• N. A. Ahmed, "A novel small scale efficient wind turbine for power generation", Renewable Energy, Vol. 57, pp. 79-85, Sep. 2013. [https://doi.org/10.1016/j.renene.2013.01.023]
• A. Ali, H. Chowdhury, B. Loganathan, and F. Alam, "An aerodynamic study of a domestic scale horizontal axis wind turbine with varied tip configurations", Procedia Engineering, Vol. 105, pp. 757-762, Jun. 2015. [https://doi.org/10.1016/j.proeng.2015.05.067]
• H. A. Madsen, J. Johansen, N. N. Sørensen, G. C. Larsen, and M. H. Hansen, "Simulation of Low Frequency Noise from a Downwind Wind Turbine Rotor", 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, pp. 7549-7560, Jan. 2007. [https://doi.org/10.2514/6.2007-623]
• Y. S. Choi, T. S. Kim, S. H. Park, H. G. Kim, M. S. Sim, and J. C. Lee, "A Study on Development of Blade for 10kW Downwind Turbine", Proceeding of the KSMPE Spring Conference, Pusan University, pp. 121, Apr. 2013.
• D. Verelst, et al., "Open Access Wind Tunnel Measurements of a Downwind Free Yawing Wind Turbine", Journal of Physics: Conference Series, Vol. 753, No. 7, pp. 072013, Sep. 2016. [https://doi.org/10.1088/1742-6596/753/7/072013]
• S. M. Larwood and R. Chow, "Comparison of upwind and downwind operation of the NREL Phase VI Experiment. Science of Making Torque from Wind", Journal of Physics : Conference Serires. Institute of Physics Publishing, Vol. 753, No 2, pp. 022041, Sep. 2016. [https://doi.org/10.1088/1742-6596/753/2/022041]
• Z. Wang, et al., "A Comparative study on the aeromechanic performances of upwind and downwind horizontal-axis wind turbines." Energy Conversion and Management, Vol. 163, pp. 100-110, May 2018. [https://doi.org/10.1016/j.enconman.2018.02.038]
• Seong-Hwan Kim and, Ick-Tae Kim, "Predicting the Generation Performance of Downwind Wind Turbine by Turbulence Modeling", The Journal of Korean Institute of Information Technology, Vol. 17, No. 3, pp. 135-142, Mar. 2019. [https://doi.org/10.14801/jkiit.2019.17.3.135]
• Seong-Hwan Kim and Kwonhee Suh, "Experimental and Numerical Investigation on Power Characteristics of 300 W Class Horizontal Axis Wind Turbine with Wave Winding Type AFPM Generator", International Journal of Precision Engineering and Manufacturing-Green Technology, Oct. 2019.
• M. Bakırcı and S. Yılmaz, "Theoretical and computational investigations of the optimal tip-speed ratio of horizontal-axis wind turbines", Engineering Science and Technology an International Journal, Vol. 21, No. 6, pp. 1128-1142, Dec. 2018. [https://doi.org/10.1016/j.jestch.2018.05.006]