전자 간 상호작용을 이용한 공간 효율적인 나노 크기의 QCA 비교기 설계

Ⅰ. 서 론

현대의 회로 설계 기술인 CMOS를 이용하여 아두이노를 비롯한 다양한 디지털 회로들이 제안되었다[1]. 하지만 CMOS는 높은 전력 소비, 발열량 등 여러 한계에 직면하였다[2]. 양자점 셀룰러 오토마타(QCA, Quantum-dot Cellular Automata)는 한계에 다다른 CMOS 보다 뛰어난 성능, 나노 크기의 회로, 그리고 적은 전력 소비의 장점들로 CMOS의 대체재로 주목받고 있다[3]. QCA 기술이 Lent 등에 의해 제시된 후, QCA를 기반으로 한 다양한 디지털 회로들이 제안되었다[4]-[14].

비교기는 입력받은 수들의 크기를 비교하는 회로이다. 비교기를 QCA 환경에서 효율적으로 설계하고자 하는 다양한 시도들이 있었으며, XOR 게이트, NAND 게이트, 또는 다층구조를 사용하는 등 다양한 형태의 비교기들이 제안되었다[11]-[14].

본 논문에서는 NAND 게이트를 사용하여 평면구조의 공간 효율적인 1비트 비교기를 제안하고, 이를 기본 소자로 하는 2비트 비교기를 제안한다.

Ⅱ. 관련 연구

2.1 QCA 기본 배경

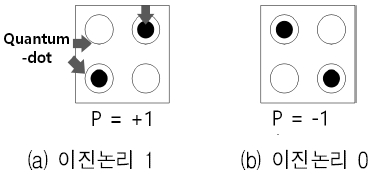
QCA의 기본적인 구성요소인 양자 셀은 네 개의 양자점으로 구성된다. 각 셀은 두 개의 전자를 가지며, 두 전자는 쿨롱반발력에 의해 서로 대각방향에 위치하게 된다[4]. 이 때 전자들은 그림 1의 (a)와 (b) 둘 중 하나와 같은 형태를 갖게 된다. 이러한 상태를 각각 +1과 –1의 편극상태라고 하며 이진논리의 1과 0에 대응된다. 특정 셀의 편극이 지정된다면, 쿨롱 반발력에 의해 인접 셀들의 편극 상태가 결정되며 신호가 전달되게 된다.

Fig. 1.

Two polarization states of the basic QCA cell, (a) Binary logical 1, (b) Binary logical 0

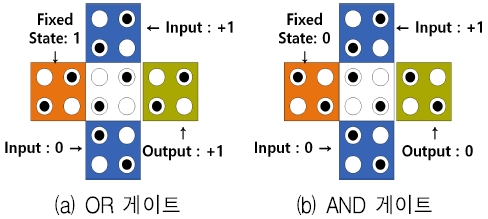
QCA 환경에서는 OR 연산과 AND 연산을 다수결 게이트를 사용하여 구현한다. 다수결 게이트는 여러 값을 입력받고 그중 다수인 값을 출력한다. 그림 2는 3개의 입력을 받는 3입력 다수결 게이트이며, (a)와 (b)는 각각 한 개의 입력을 1과 0으로 고정시켜 OR 게이트와 AND 게이트로 동작한다.

Fig. 2.

3-input majority gate, (a) OR gate, (b) AND gate

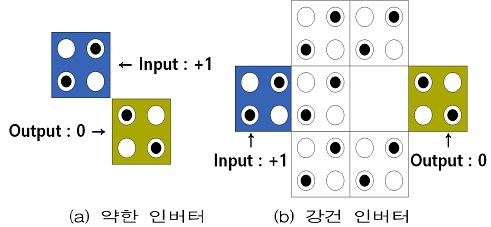
인버터는 그림 3의 (a)와 (b) 형태로 구현 할 수 있다. (a)는 약한 인버터로 필요 면적이 작지만 신호가 약하게 전달되며, (b)는 강건 인버터로 신호가 강하게 전달되지만, 공간을 많이 차지한다.

Fig. 3.

Inverter, (a) Weak inverter, (b) Robust inverter

2.2 QCA NAND 게이트

본 논문에서는 비교기를 설계하기 위해서 QCA NAND 게이트를 사용한다. QCA 환경에서는 AND 게이트의 결과값에 인버터를 이용하는 기본적인 형태 이외에도, 독자적인 형태의 NAND 게이트들이 제안되었다[9].

본 논문에서 제안된 비교기는 그림 4와 같이 [10]에서 B. Sen 등이 제안한 평면구조의 공간 효율성이 뛰어난 NAND 게이트를 사용한다.

Fig. 4.

Proposed NAND gate in [10]

Ⅲ. 비교기 설계

3.1 QCA 1비트 비교기 설계

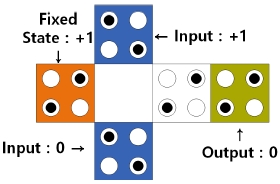
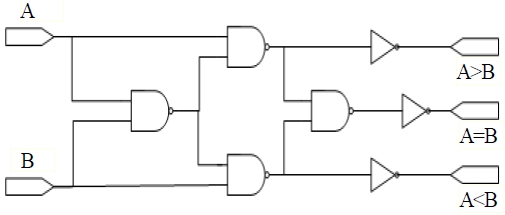
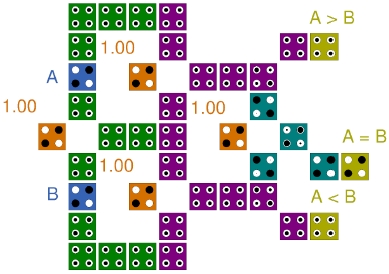
본 논문에서는 NAND 게이트를 사용하여 공간 효율적인 1비트 비교기를 제안하고, 제안하는 1비트 비교기를 나노 크기로 하여, 2비트 비교기를 제안한다. 그림 5는 NAND 게이트를 이용하여 제안하는 1비트 비교기의 논리도이며, 이 논리도를 바탕으로 그림 4의 QCA NAND 게이트와 그림 3(a)의 인버터를 이용하여 그림 6의 QCA 회로를 제안한다.

Fig. 5.

Logic diagram of proposed 1-bit comparator circuit

Fig. 6.

Proposed QCA 1-bit comparator circuit

이 회로는 1비트 두 개의 입력 A, B를 받아, A < B, A = B, A > B 세 가지의 출력값 중 하나만 1을 출력해주는 동작을 수행하며 그 결과들은 표 1에 진리표로 나타냈다.

Table 1.

Truth table of NAND gate-based 1-bit comparator

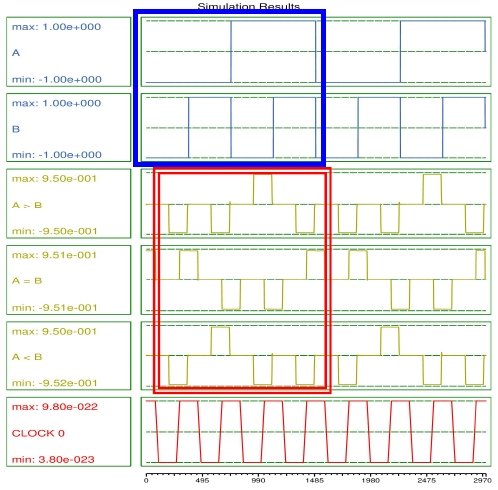
그림 7은 제안하는 비교기의 시뮬레이션 결과이며, 그림 상단의 □ 상자 내부의 입력에 따라서, 그림 하단의 ⧈ 상자 내부에 결과값이 산출된다. 시뮬레이션 결과와 진리표를 비교해보면 서로 일치한다는 것을 알 수 있고, 따라서 그림 6의 회로는 정상적으로 동작하는 것을 확인 할 수 있다.

Fig. 7.

Simulation result of proposed 1-bit comparator

3.2 QCA 2비트 비교기 설계

제안한 1비트 비교기를 기본 소자를 사용하여 2비트 비교기를 설계한다. 이 회로는 최상위 비트 A0와 B0, 그리고 최하위 비트 A1과 B1으로 구분되는 2비트 입력값 A, B를 입력받는다. 이 2비트 입력 값 A와 B를 비교하기 위해서 최상위 비트인 A0와 B0, 그리고 최하위 비트인 A1과 B1을 각각 따로 비교한다. 만약 최상위 비트, 즉, A0와 B0가 다르다면, A와 B의 크기 비교는 A1과 B1에 관계없이 결정된다. 하지만 A0와 B0가 같다면 최하위 비트인 A1과 B1의 비교 결과로 A와 B의 크기 비교가 결정된다.

예를 들어, A < B 라는 결과는 최상위 비트 A와 B의 비교 결과가 A0 < B0인 경우 또는, A0 = B0 이면서 A1 < B1 일 때, 이 두 가지 경우에 성립하게 된다. 이를 부울 대수로 표현한다면 수식 (1)과 같다.

그러나 본 논문에서 제안하는 2비트 비교기는 그림 6의 1비트 비교기를 나노 크기로 사용하며, 이 소자는 모든 출력값들이 출력 전 인버터를 거치는 형태이다. 인버터 구조가 야기하는 신호의 약화와 필요공간의 증가를 막기 위하여 드모르간의 법칙을 사용하여 수식을 변경하였다. 수식 (1)은 드모르간의 법칙을 사용하여 변형하면, (2)와 (3)을 거처 최종적으로 (4)의 수식으로 변형 할 수 있다.

(1)

(2)

(3)

(4)

A = B의 경우는 최상위 비트 A0와 B0가 일치하고, 최하위 비트 A1와 B1가 모두 같을 때만 성립하게 된다. 이는 (5)의 수식으로 표현되며, 드모르간의 법칙을 사용하여 (6)의 형태로 변형할 수 있다. (4)와 (6)의 수식을 사용함으로 해서, 나노 크기의 출력값에 사용되던 인버터들을 사용하지 않도록 회로를 설계할 수 있다.

$\[ \left(A0=B0\right)\cdot \left(A1=B1\right) \]$

(5)

$\[ \left(\left(A0=B0\right)\text{'}+\left(A1=B1\right)\text{'}\right)\text{'} \]$

(6)

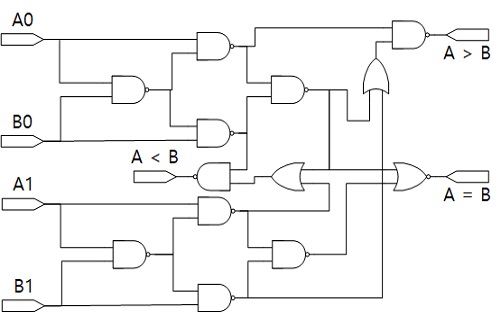
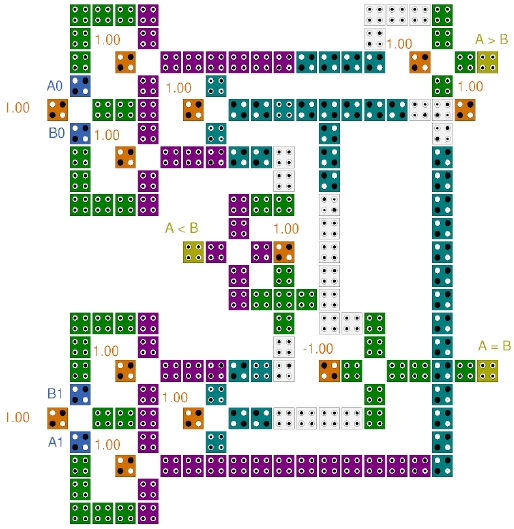
이러한 원리를 이용하여 그림 8의 논리도를 구성하였고, 구성한 논리도를 바탕으로 그림 9의 QCA 2비트 비교기 회로를 설계하였다.

Fig. 8.

Logic diagram of proposed 2-bit comparator

Fig. 9.

QCA circuit of proposed 2-bit comparator

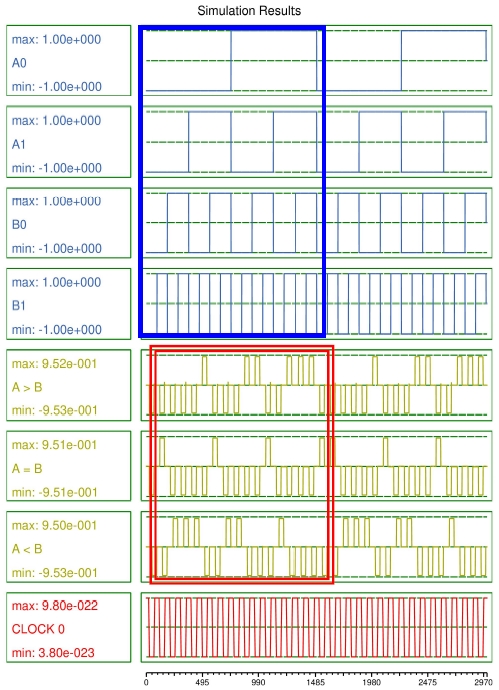
그림 10은 제안하는 2비트 비교기의 시뮬레이션 결과이다. 그림 10에서 그림 상단의 □ 상자 내부의 각각 A0와 B0를 최상위 비트로 하는 2비트 입력 A와 B에 따라서, 그림 하단의 ⧈ 상자 내부에 정상적인 결과를 출력하는 것을 확인할 수 있다.

Fig. 10.

Result of proposed QCA 2-bit comparator simulation

Ⅳ. 비교 및 분석

표 2는 본 논문에서 제안된 1비트 비교기와 기존의 1비트 비교기들의 성능을 보여준다[8][11]-[14]. 표 2에서, 제안하는 1비트 비교기와 기존의 회로를 비교해보면 제안된 회로는 필요 면적과 셀 수에서 각각 최소 29%, 31% 가량의 성능이 향상되었으며, 지연 시간은 동일하거나 우수한 것을 볼 수 있다. 그리고 제안하는 2비트 비교기는 필요 면적이 0.174μm², 셀 수 167개, 그리고 지연시간은 1.5 클럭 사이클이며, 이는 [13]에서 제안된 2비트 비교기보다 0.121μm²의 필요 면적, 93개의 셀 수, 1 클럭 사이클의 성능향상을 보인다.

Table 2.

1-bit comparator performance analysis and comparison

Ⅴ. 결론 및 향후 과제

본 논문에서는 QCA 환경에서 NAND 게이트를 사용하여 공간 효율적인 1비트 비교기를 설계하였다. 제안하는 1비트 비교기는 기존의 비교기보다 지연시간이 작거나 같고, 필요 공간과 필요 셀 수가 줄어든 것을 확인했다. 이 회로를 나노 크기로 하여 2비트 비교기를 설계하였으며, 이때 인버터의 사용으로 야기될 수 있는 신호의 약화를 최소화하기 위해, 드모르간의 법칙을 사용하여 논리를 정리했다. 그로 인해 나노 크기의 출력 부분에 사용되던 6개의 인버터들을 사용하지 않을 수 있었다. 비교기를 확장해 본 결과, 본 논문에서 제안하는 회로가 간단하게 확장될 수 있음을 확인하였으며, 비교를 통해 공간적인 성능이 향상됨을 확인 할 수 있었다.

향후 본 논문에서 제안한 비교기들을 기본 소자로 더 큰 규모의 공간 효율적인 비교기를 설계할 수 있을 것이다. 이는 차세대 컴퓨터 환경을 구축하는 데에 기여할 수 있을 것이다.

Acknowledgments

이 논문은 2019년도 정부(교육부)의 재원으로 한국과학창의재단(2019년도 학부생 연구프로그램)의 지원을 받아 수행된 연구임.

References

• K. M. Cho and T. K. Kim. "Implementation of an RF-based Traffic Safety Marking System using Arduino", Journal of JAITC, Vol. 7, No. 2, pp. 11-22, Dec. 2017. [https://doi.org/10.14801/jaitc.2017.7.2.11]
• N. Z. Haron and S. Hamdioui, "Why is CMOS scaling coming to an END?", 2008 3rd International Design and Test Workshop, IEEE, Monastir, Tunisia, pp. 98-103, Dec. 2008. [https://doi.org/10.1109/IDT.2008.4802475]
• J. C. Jeon, "Low Complexity QCA Universal Shift Register Design Using Multiplexer and D Flip-Flop Based on Electronic Correlations", The Journal of Supercomputing, pp. 1-15, Aug. 2019. [https://doi.org/10.1007/s11227-019-02962-y]
• C. S. Lent, P. D. Tougaw, and W. Porod, "Bistable saturation in coupled quantum dots for quantum cellular automata", Applied Physics Letters, Vol. 62, No. 7, pp. 714-716, Feb. 1993. [https://doi.org/10.1063/1.108848]
• N. Safoev and J. C. Jeon, "A Novel Controllable Inverter and Adder/Subtractor in Quantum-Dot Cellular Automata Using Cell Interaction Based XOR Gate", Microelectronic Engineering, Vol. 222, Feb. 2020 [https://doi.org/10.1016/j.mee.2019.111197]
• S. Erniyazov and J. C. Jeon, "Carry save adder and carry look ahead adder using inverter chain based coplanar QCA full adder for low energy dissipation", Microelectronic Engineering, Vol. 211, pp. 37-43, Apr. 2019. [https://doi.org/10.1016/j.mee.2019.03.015]
• N. Safoev and J. C. Jeon, "Design of high-performance QCA incrementer/decrementer circuit based on adder/subtractor methodology", Microprocessors and Microsystems, Vol. 72, Feb. 2020. [https://doi.org/10.1016/j.micpro.2019.102927]
• Q. Ke-ming and X. Yin-shui, "Quantum-dots cellular automata comparator", In 7th International Conference on ASIC, IEEE, Guilin, China, pp. 1297-1300, Oct. 2007. [https://doi.org/10.1109/ICASIC.2007.4415874]
• M. Raj and L. Gopalakrishana, "Design and Defect Analysis of Novel NAND/NOR Gate in Quantum-dot Cellular Automata", 2018 International Conference on Circuits and Systems in Digital Enterprise Technology, IEEE, Kottayam, India, India, pp. 1-5, Dec. 2018. [https://doi.org/10.1109/ICCSDET.2018.8821116]
• B. Sen and B. K. Sikdar, "Characterization of universal NAND-NOR-inverter QCA gate", Proceedings of 11th IEEE VLSI Design and Test Symposium, Kolkata, India, pp. 433-442, Oct. 2007.
• B. Ghosh, S. Gupta, and S. Kumari, "Quantum dot cellular automata magnitude comparators", In 2012 IEEE International Conference on Electron Devices and Solid State Circuit, IEEE, Bangkok, Thailand, pp. 1-2, Dec. 2012. [https://doi.org/10.1109/EDSSC.2012.6482766]
• Md. Abdullah-Al-Shafi, A. N. Bahar, and Q. Ai, "Optimized Design and Performance Analysis of Novel Comparator and Full Adder in Nanoscale", Cogent Engineering, Vol. 3, No. 1, pp. 1-14, Sep. 2016. [https://doi.org/10.1080/23311916.2016.1237864]
• C. S. Park, D. K. Seo, S. H. Yoon, W. Y. Jang, and J. C. Jeon, "Design of 1-Bit Comparator Using QCA Universal NAND Gate", 2019 Joint Conference DCS & KIIT, Chunan, South Korea, pp. 170–171, Nov. 2019.
• S. Erniyazov and J. C. Jeon, "Area Effcient Magnitude Comparator Based on QCA", Advanced Science and Technology Letters, Vol. 150, pp. 75-79, Feb. 2018. [https://doi.org/10.14257/astl.2018.150.19]