Design and Analysis of Fast Fourier Transform Processors with Various Number Systems

Ⅰ. Introduction

The fast Fourier transform (FFT) algorithm is widely used in orthogonal frequency-division multiplexing (OFDM) systems such as wireless LAN, digital video broadcasting and digital audio broadcasting[1][2]. Important VLSI design considerations of FFT processors are the performance and cost such as output latency, gate count, memory size and signal-to-quantization-noise ratio (SQNR). In order to design FFT processors with high performance and low cost, we should consider the type of number system and the word length of the FFT as well as specifications of target applications. This is because the performance and cost of FFT processors are heavily influenced by the type of number system and the word length used.

In general, the performance and cost of a FFT processor depend heavily on whether the FFT processor adopts a fixed-point or floating-point number system[2]. FFT processors have traditionally used fixed-point number systems because of the high cost associated with implementing floating-point number systems. Nowadays, however, certain applications such as synthetic-aperture radar systems, which require a high degree of accuracy, demand a large dynamic range offered by the floating-point number system, despite the cost increase caused by high circuit complexity for the floating-point number system[3]. Due to improvement on IC process technology as well as the above-mentioned need for the high precision and large dynamic range, floating-point number systems become more and more widely used in FFT processors.

The theoretical performance analysis of the FFT can be found in previous researches. Pankaj Gupta presented a statistical method for evaluating fixed point performance of Radix-2 FFT implementation[4]. O. Sarbishei and K. Radecka provided an efficient analysis of mean square error as well as an optimization algorithm for FFT units[5]. Chang and Nguyen investigated the effect of fixed-point arithmetic with limited precision on different fast FFT algorithms[6]. Khan et al. calculated the performance of the FFT based on fixed-point and floating-point formats using statistical or simulation methods[7]. Pagiamtzis and Gulak provided an empirical estimation method for FFT blocks in multicarrier systems[8]. In contrast to the previous works, one of the primary goals of this research is to analyze the influence on the performance and cost of FFT processors as a function of the type of number system and the word length of the FFT through practical analysis of VLSI designs of FFT processors in terms of SQNR, output latency, memory size and gate counts. From the experimental results, we found that the SQNRs of the floating-point FFT processors is 47.7% higher compared with that of the fixed-point FFT processor. However, fixed-point FFTs require the lowest output latencies. In the case of the average memory size of the floating-point FFT is larger by 46.9% than those of the fixed-point FFT. The average gate count of the floating-point FFT processors is larger by 67.6% compared with the fixed-point FFT processors.

Ⅱ. Number Systems of the FFT

A number system is defined by the set of values that each digit can assume and by the interpretation rule that defines the mapping between the sequences of digits and their numerical values[9]. A fixed-point number system has several advantages. A FFT processor based on a fixed-point number system performs additions and multiplications more simply than a FFT processor based on a floating-point number system. Also, given that inputs of the FFT processor have a small dynamic range, the FFT processor based on a fixed-point number system provides sufficient numerical precision, with a reasonable number of bits. On the contrary, for inputs with a large dynamic range, the FFT processor requires a floating-point number system. Moreover, The FFT processor based on a floating-point can be designed with less attention paid to the dynamic range of intermediate variables. However, a floating-point number system has the disadvantage that multiplications and additions are complex, thus increasing the cost[9].

In order to extend the dynamic range of a number system, block floating-point (BFP) number systems are often used in FFT processors[10]. The BFP number system can be considered as a special case of the floating-point representation, where a block of numbers has a common exponent[11]. A BFP FFT processor does not use exponents as inputs. Thus, each number in the BFP FFT processor can be expressed in two components, a mantissa and a common exponent. The common exponent is determined by the number with the largest magnitude and stored as a separate data word. Therefore, each stage of the BFP FFT processor determines the value of the common exponent by calculating the number of leading bits of each intermediate number and detecting the largest number. By scaling each value using the common exponent, the BFP increases the dynamic range of data elements with moderate hardware overhead.

Ⅲ. Architectures of FFT Processors with Various Number Systems

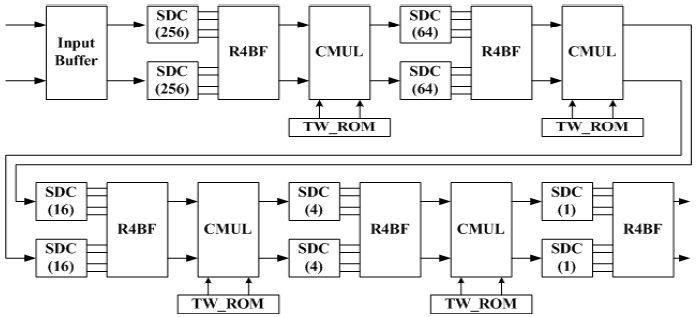
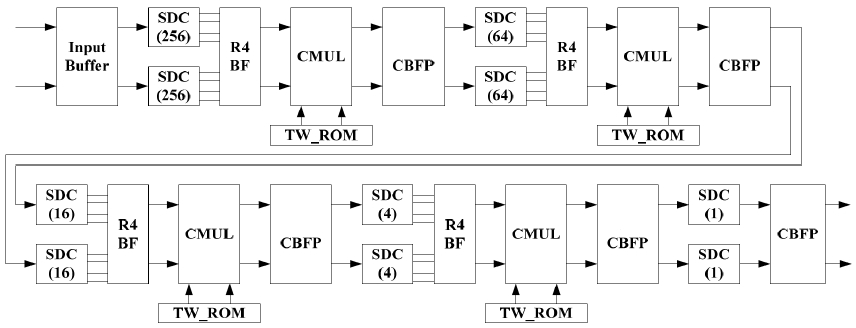
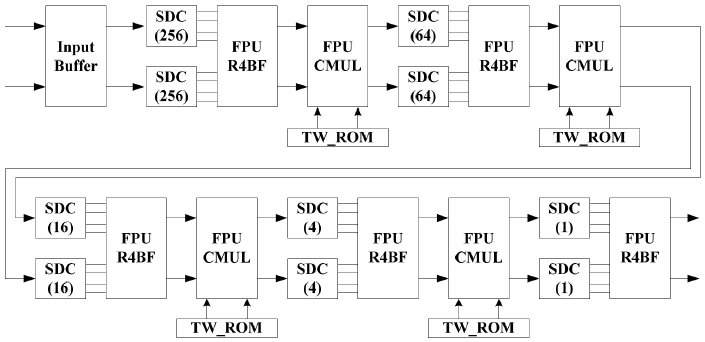
In this section, we describe the architectures of pipeline FFT processors. FFT processors based on Cooley-Turkey algorithm are widely used because of its significant computational reduction from O(N2) to O(NlogN), where N is the length of the FFT, and there are various FFT architectures utilizing pipeline or systolic array technique[10]. Among them, pipeline FFT architectures are widely used in high throughput, real-time and non-stopping processing applications. For these reason, we design pipeline FFT processors based on Cooley-Turkey algorithm, and use these for all of the experimental procedures. Figs. 1, 2 and 3 show the proposed architectures of the 1024-length fixed-point, BFP and floating-point FFT processors, respectively.

Fig. 1.

Architecture of the 1024-length fixed-point FFT processor

Fig. 2.

Architecture of the 1024-length CBFP FFT processor

Fig. 3.

Architecture of the 1024-length floating-point FFT

Pipeline FFT processors consist of complex multipliers, butterfly units, and delay commentators rearranging the orders of intermediate results after each stage of the FFT[12]. According to the radix of the FFT and the architecture of the delay commutator, FFT architectures are classified into radix-2 multi-path delay commutator, radix-2 single-path delay feedback, radix-4 single-path delay feedback, radix-4 multi-path delay commutator, radix-4 single-path delay commutator (R4SDC), etc.[13].

The R4SDC architecture is suitable for FFT processors using the decimation in frequency algorithm. That is because complex multipliers are used after butterfly operation of each stage of the FFT. As shown in Fig. 1, the 1024-length fixed-point FFT processor based on the R4SDC consists of single-path delay commutators (SDCs), which are rearranging the orders of intermediate data for radix-4 butterfly units (R4BFs), twiddle factor lookup tables which are located in ROMs (TW ROMs) and complex multipliers (CMULs). The FFT processor based on the R4SDC architecture achieves 100% utilization of the complex multipliers and 75% utilization of the butterfly elements[13].

In general, the disadvantage of the FFT processor based on a fixed-point number system is that intermediate results after each stage of the FFT are often saturated or truncated, due to its limited internal word length. Indeed, this saturation or truncation causes accuracy degradation of data. In order to increase the accuracy, convergent BFP (CBFP) algorithm is often used[10]. The FFT processor based on a CBFP number system uses one global exponent per block of each stage of the FFT. Fig. 2 shows the 1024-length FFT processor based on the BFP number system that has a CBFP unit after each stage.

For higher precision and larger dynamic range, floating-point number systems can be used in FFT processors. Fig. 3 shows the 1024-length floating-point FFT processor. Whereas arithmetic modules such as R4BF and CMUL of Fig. 1 and 2 have only one pipeline stage, the arithmetic modules based on the floating-point number system have three stages, in order to make its frequency comparable to those of the fixed-point and CBFP FFT processors.

Ⅳ. Experimental Results

4.1 Experimental Procedure

We design 64-, 256- and 1024-length FFT processors based on the fixed-point, BFP, and floating-point number systems with the 0.18-μm complementary metal-oxide-semiconductor (CMOS) technology and measure the performance and cost of the FFT processors using the various metrics such as the latency, SQNR, gate counts and memory size.

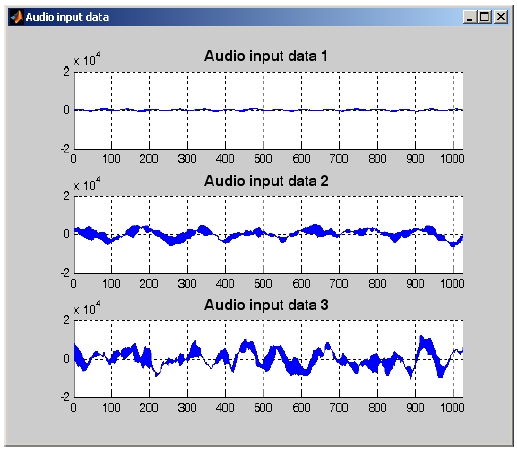
First, we measure the SQNR of the FFT processors because the SQNR is an appropriate performance metric to measure the relative performance of the FFT processors. Three types of input streams shown in Fig. 4 are used to measure the SQNR and to compare the performance of the FFT processors considering the variation of the amplitude of the inputs. Second, we measure the output latency, which is also an important performance metric of the FFT processor. Third, we measure the memory size and gate counts to know trade-offs between the performance and cost of the FFT processors that the number systems have.

Fig. 4.

Three types of input streams

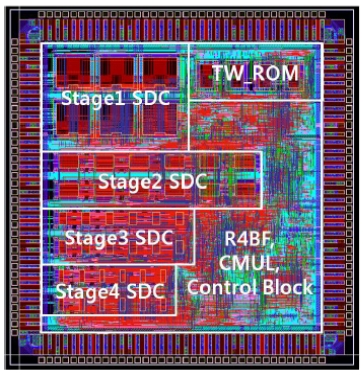
The gate counts are calculated from the results of logic synthesis using the 0.18-μm CMOS library. For the reliability of the design, we implemented the 1024-length FFT processor based on the fixed-point number system using the 0.18-μm CMOS library. Fig. 5 shows the layout of the 1024-length FFT processor based on the fixed-point number system.

Fig. 5.

Layout of the 1024-length FFT processor based on the fixed-point number system

4.2 SQNR

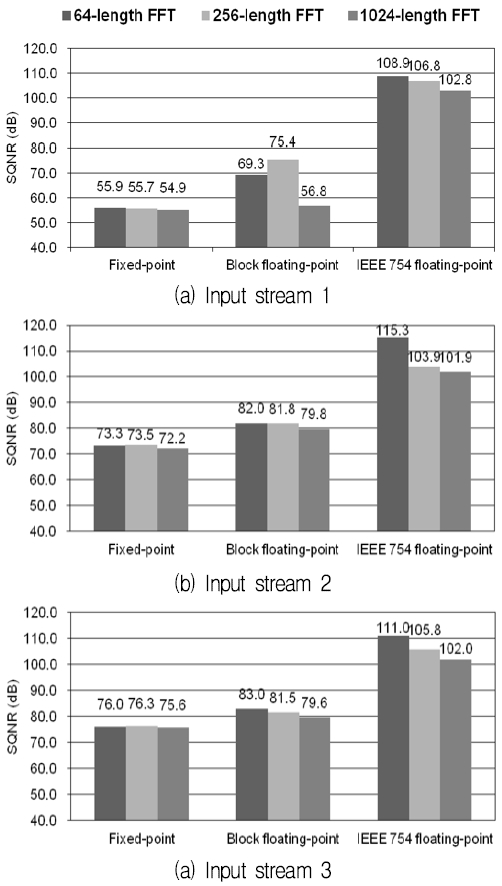
Fig. 6(a) shows the SQNR results for the first input stream. The average SQNRs of the CBFP and IEEE 754 floating-point FFT processors are 17.4% and 47.7% higher, respectively, compared with that of the fixed-point FFT processor, as shown in Table 1.

Fig. 6.

SQNR results of the FFT according to the input stream

Table 1.

SQNR improvement ratio of the CBFP and IEEE 754 floating-point FFT compared with the fixed-point FFT

As shown in Fig. 6(b), for the second input stream, the average SQNRs of the CBFP and IEEE 754 floating-point FFT processors are higher by 10.1% and 31.8%, respectively, compared to that of the fixed-point FFT processor. Similarly, for the third input stream, the CBFP and IEEE 754 floating-point FFT processors have SQNRs higher by 6.6% and 28.3%, respectively, than the fixed-point FFT processor, as shown in Fig. 6(c).

In case of the fixed-point and CBFP FFT processors, the average SQNRs for the first input stream show considerable degradation compared to the average SQNR for the second and third input streams. This is because error sensitivity in the first input stream is relatively large compared to the other input streams. In contrast, in the IEEE 754 floating-point FFT processors, the type of input streams have little impact on the SQNRs, due to its high precision and large dynamic range. Putting it all together, the IEEE 754 floating-point FFT processor has relatively large benefits when the input stream has a large distribution range.

4.3 Output Latency

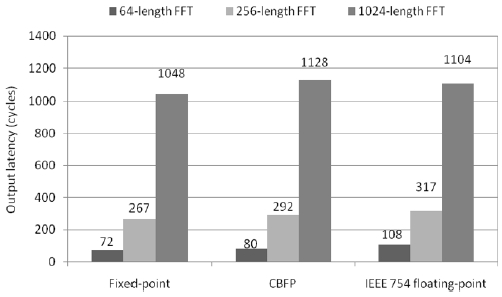
Cycle times of all the FFTs are set to 10 s for the pair comparison. In order to make the same cycle time of all the FFTs, The arithmetic modules of the floating-point FFT have three pipeline stages. Then, we measure the output latency as total number of cycles taken from the inputs to the outputs. As shown in Fig. 7, the fixed-point FFTs require the lowest average output latencies, whereas the IEEE 754 floating-point FFTs do the highest. However, in case of the length of 1024, the output latency of the CBFP FFT is higher than those of the other two. This is because each stage of the CBFP FFT requires additional cycles to detect the common exponent and scale the intermediate result. These additional cycles occupy a larger portion of the output latency as the FFT length increases.

Fig. 7.

Output latencies of the FFTs as a function of the type of number system and FFT length

4.4 Memory Size

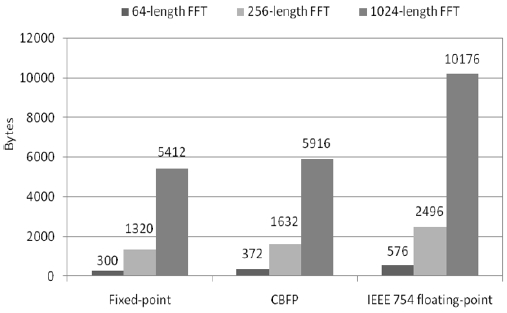
Fig. 8 shows that the average memory sizes of the fixed-point, CBFP and IEEE 754 floating-point FFTs are 2344, 2640 and 4416 bytes, respectively. The results show that the average memory size of the CBFP FFTs is larger by 11.2% compared with the fixed-point FFTs. The average memory size of the IEEE 754 floating-point FFTs is larger by 46.9% and 40.2% than those of the fixed-point and the CBFP FFTs, respectively.

Fig. 8.

Memory sizes as a function of the type of number system and FFT length

4.5 Gate Count

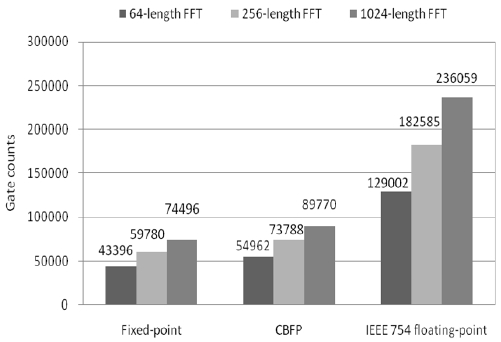
We measure the gate counts required to implement the FFT processors to estimate the cost of the FFT processor. As shown in Fig. 9, the average gate counts of the fixed-point, CBFP and IEEE 754 floating-point FFT processors are 59224, 72840 and 182549, respectively.

Fig. 9.

Gate counts as a function of the type of number systems and FFT length

These results indicate that the average gate count of the CBFP FFT processors is larger by 18.7% compared with the fixed-point FFT processors. Besides, as compared with the fixed-point and the CBFP FFT processors, the average gate count of the IEEE 754 floating-point FFT processors is larger by 67.6% and 60.1%, respectively. This indicates that the IEEE 754 floating-point FFT processors have a problem of high cost, despite their high performance.

4.6 Proposition of a Cost- and Performance-Effective Word Length of the Floating-Point Number System

To propose a cost-effective word length of the floating-point number system for FFT processors, we measure the performance and cost of the FFT processors based on the floating-point number systems with a variety of bit widths of the fraction and exponent. The results show that seven, eight and nine-bit exponents have almost the same performance, so that the exponent is fixed to seven bits in the experiments for the suggestion of a cost-effective word length of the floating-point number system.

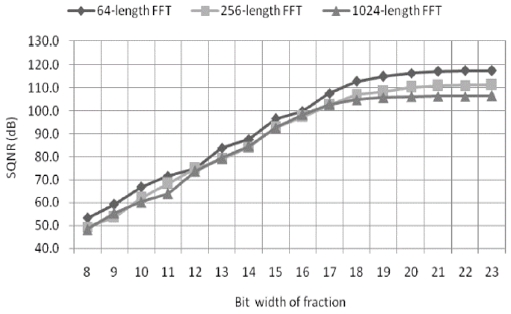
Fig. 10 shows the SQNRs of the floating-point FFT processors with various bit widths of the fraction from 8 to 23. It is clear that when the bit width of the fraction is over 18, SQNRs are almost saturated. This saturation is mainly due to the finite word length of the number system and the propagation of quantization noise through an FFT architecture based on non-infinity errors induced from the FFT computations.

Fig. 10.

SQNR of the floating-point FFT as a function of the fraction bit width

Therefore, the experimental results of the SQNRs are different from those obtained from theoretical analysis of the SQNRs that are based on infinity errors induced from the FFT computations. From those observations, we can find that the floating-point number system provides enough precision for the FFT if the bit width of the fraction is over 18, whereas the memory size and gate counts increases almost linearly with the bit width of the fraction.

In order to investigate the above results in details, Fig. In order to investigate the above results in details, Fig. 11 shows the relative performance and cost of the floating-point FFT processors, where those of the IEEE 754 single-precision FFT processor are used as criterions.

Fig. 11.

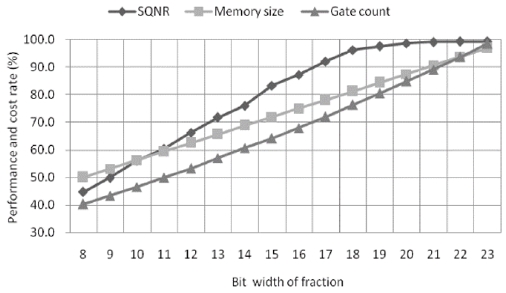
Relative performance and cost of the floating-point FFTs normalized to the IEEE 754 floating-point FFT

When the bit width of the fraction is greater than or equal to 11, the relative SQNR, which is the performance metric, is higher than the relative memory size and gate count, which are the cost indices. Especially, the ratio of performance to cost is the maximum when the bit width of the fraction is 18. Thus, we can conclude that the 18-bit fraction is the most cost- and performance-effective floating-point number system. Furthermore, the floating-point FFT processor with an 18-bit fraction has almost the same performance with 80% cost compared with the IEEE 754 floating-point FFT processor.

Ⅴ. Conclusion

We have presented a comparative study of performance and cost of the FFT based on the various number systems using the practical investigation. Moreover, the in-depth explorations of the trade-offs between the performance and cost of the floating-point FFT processors have been carried out with emphasis on the experimental results of the SQNRs. From the experimental results, it is clear that the CBFP FFT processors produce improved quantization error over the fixed-point FFT processors. In addition, the floating-point FFT processors have the highest cost, whereas they have the highest performance. So, we investigated the cost- and performance-effective word length of the floating-point number system. The experimental results have confirmed that the number system and word length of the FFT have a great influence on the cost and performance, and it is not quite easy to find the appropriate number systems and word length of the FFT for applications which have various requirement specifications. From the experimental results, we found that the 7-bit exponent and 18-bit fraction are the most cost- and performance-effective floating-point number system. Therefore, our study will be useful for designing a high-performance FFT processor for OFDM systems.

Acknowledgments

This research was supported by Multi-Ministry Collaborative R&D program (R&D program for comoplex cognitive technology) through the National Research Foundation of Korea (NRF) funded by the Ministry of Trade, Industry and Energy (NRF-2018M3E3A1057248).

References

• W. H. Choi and S. J. Lee, "Cognition of FM Wireless Microphone Signal Using Autocorrelation Function and FFT", The Journal of Korean Institute of Information Technology, Vol. 10, No. 11, pp. 81-88, Nov. 2012.
• W. Smith, "Digital signal processing", San Diego, California Technical Publishing, 1999.
• J. Zhou, Y. Dong, Y. Dou, and Y. Lei, "Dynamic Configurable Floating-Point FFT Pipelines and Hybrid-Mode CORDIC on FPGA", 2008 International Conference on Embedded Software and Systems, Sichuan, China, pp. 616-620, Jul. 2008. [https://doi.org/10.1109/ICESS.2008.95]
• P. Gupta, "Accurate performance analysis of a fixed point FFT", 2016 Twenty Second National Conference on Communication (NCC), Guwahati, India, pp. 1-6, Mar. 2016. [https://doi.org/10.1109/NCC.2016.7561147]
• O. Sarbishei and K. Radecka, "On the Fixed-Point Accuracy Analysis and Optimization of FFT Units with CORDIC Multipliers", 2011 IEEE 20th Symposium on Computer Arithmetic, Tubingen, Germany, pp. 62-69, Aug. 2011. [https://doi.org/10.1109/ARITH.2011.17]
• W. H. Chang and T. Q. Nguyen, "On the fixed-point accuracy analysis of FFT algorithms", IEEE Trans. on Signal Processing, Vol. 56, No. 10, pp. 4673-4682, Oct. 2008. [https://doi.org/10.1109/TSP.2008.924637]
• A. U. Khan, M. M. Al-Akaidi, S. A. Khan, S. Khattak, and A. Mir, "Performance analysis of a 64-point FFT/IFFT block designed for OFDM technique used in WLANs", 7th International Multi Topic Conference, Islamabad, Pakistan, pp. 65-71, Dec. 2003.
• K. Pagiamtzis and P. G. Gulak, "Empirical performance prediction for FFT/IFFT cores for OFDM systems-on-a-chip", Proceeding of the 45th Midwest Symposium on Circuits and Systems, Tulsa, OK, USA, Vol. 1, pp. 583-586, Aug. 2002.
• I. Koren, "Computer arithmetic algorithm", 2th ed. Massachusetts, A K Peters, 2002.
• E. Bidet, D. Castelain, C. Joanblanq, and P. Senn, "A fast single-chip implementation of 8192 complex point FFT", IEEE Journal of Solid-State Circuits, Vol. 30, No. 3, pp. 300-305, Apr. 1995. [https://doi.org/10.1109/4.364445]
• K. Kallioj¨arvi and J. Astola, "Roundoff errors in block-floating-point systems", IEEE Transaction on Signal Processing, Vol. 44, No. 4, pp. 783-790, Apr. 1996. [https://doi.org/10.1109/78.492531]
• S. He and M. Torkelson, "A new approach to pipeline FFT processor", in Proceedings of International Conference on Parallel Processing, Honolulu, HI, USA, pp. 766-770, Apr. 1996.
• S. He and M. Torkelson, "Design and implementation of a 1024-point pipeline FFT processor", in Proceedings of the IEEE 1998 Custom Integrated Circuits Conference, Santa Clara, CA, USA, pp. 131-134, May 1998.