개선된 컨텍스트기반 퍼지 클러스터링을 이용한 점진적 입자모델의 설계와 자동적인 지식생성
초록
본 논문은 점진적 입자 모델을 설계하기 위해 선형회귀(LR: Linear Regression)와 국소 입자모델(LGM: Local Granular Model)을 결합한다. 여기서, 국소 입자모델은 자동적인 지식생성을 위해 밀도 피크의 빠른 탐색에 근거한 컨텍스트기반 퍼지 클러스터링(Context-based fuzzy clustering)에 의해 설계되어진다. 이 클러스터링방법은 선형회귀에서 얻어진 예측 오차정보로부터 출력의 정보입자(Information granules)를 생성하고 밀도 피크들을 빠르게 탐색하여 각 정보입자에 대응하는 타당한 클러스터들을 구할 수 있다. 이렇게 함으로써, 각 컨텍스트에서 생성되는 클러스터의 수가 같게 되는 문제점을 해결할 수 있으며, 각각의 클러스터들은 국소 입자모델의 특성을 나타내는 언어적인 퍼지 if-then규칙으로써 사용되어진다. 예측 성능평가를 위해, 비선형회귀문제인 실세계 응용을 다루고 제안된 점진적 입자모델의 설계에서 효율적인 지식생성을 통해 유용성과 우수성을 증명하고자 한다.
Abstract
This paper is concerned with the combination of Linear Regression (LR) and the Local Granular Model (LGM) to design incremental granular model. Here, the LGM is designed by context-based fuzzy clustering based on rapid search of density peaks to generate the automatic knowledge. This clustering generates information granules of output from the error information obtained by linear regression and it can obtain the valid clusters corresponding to each information granule by rapidly searching density peaks. Thus, we can solve the problem that the number of cluster generated in each context is same. Moreover, each cluster can be used as linguistic fuzzy if-then rules representing characteristics of LGM. In order to evaluate the prediction performance, the experiments are performed on real-world application of nonlinear regression problem to demonstrate the superiority and effectiveness through the efficient knowledge generation in the design of incremental granular model.
Keywords:
automatic knowledge generation, incremental granular model, local granular model, information granulesⅠ. 서 론
입자 컴퓨팅은 정보처리분야에서 새롭게 부각되는 컴퓨팅 패러다임이다. 이것은 실세계 응용문제에 대해서 정보와 지식을 가지고 효과적인 계산 모델을 설계하기 위해서 클러스터, 부분집합, 구간, 그룹, 클래스와 같은 정보입자를 이용하는 것에 대한 계산적인 이론이다. 이와 관련된 연구는 프로그램에서의 정보은닉, 인공지능에서의 입자성, 계산 과학에서 분할정복 알고리즘, 구간 컴퓨팅, 클러스터 분석, 퍼지와 러프 집합이론, 데이터베이스 등의 많은 관련된 분야에서 연구가 수행되어지고 있다. 여기서 집합이론, 퍼지집합, 러프집합에서 형성되는 정보입자들의 잘 정립된 개념을 이용하는 것은 실세계 응용문제를 해결하는 데에 직접적인 도움이 된다[1]-[5].
입자 컴퓨팅의 계산적인 플랫폼을 형성하기 위해 본 논문에서는 정보입자들에 의해 실현되는 컨텍스트기반 퍼지 클러스터링을 이용한 점진적 입자 모델의 설계 방법론을 발전시키고자 한다. 이 모델은 간단한 선형회귀와 국소인 입자모델을 결합하여 설계되어지고 있다. 특히 국소인 입자모델은 정보입자의 기본적인 개념을 가지고 입력과 출력공간으로부터 형성되는 데이터간의 상관관계를 근거로 해서 설계되어진다. 여기서 출력공간에서 생성되는 컨텍스트는 언어적인 값을 가진 퍼지집합의 형태이며, 국소 입자모델의 가중치로 사용된다. 이들 컨텍스트는 사용자중심의 컴퓨팅 방법으로써 시스템의 개발자에 의해 조정되어질 수 있다. 각각의 컨텍스트에 포함되는 입력데이터에 대해서 컨텍스트기반 퍼지 클러스터링이 수행하여 클러스터들을 생성하고, 국소인 입자모델의 특성을 반영한 규칙을 얻는다.
점진적 입자 모델의 유용성은 이전 연구에서 증명되었다할지라도, 클러스터 생성을 통한 지식생성은 몇 가지 문제점을 가지고 있다[6]-[8]. 이러한 문제점은 이전 연구에서 국소인 입자모델은 각 컨텍스트에 대응하는 클러스터의 수가 같다는 가정하에서 설계되어진다. 즉, 각 컨텍스트에서 포함된 데이터들의 특성은 반영되지 못하고 클러스터링이 수행된다는 문제점을 가지고 있다[6].
다른 한편으로 최근에 클러스터의 생성에서 밀도 피크의 빠른 탐색에 근거한 방법이 부각되고 있다. 이 접근은 클러스터 중심들이 고밀도를 가진 포인트로부터 상대적으로 먼 거리에 존재하고 있으며, 저밀도를 가진 이웃에 의해 둘러싸여 있다는 특징을 가지고 있다[9]. 이러한 개념을 근거로 각 컨텍스트에 대응하는 타당한 클러스터의 수를 얻도록 개선하고 퍼지 if-then규칙형태인 자동적인 지식을 생성하고자 한다.
그러므로 본 논문은 밀도 피크의 빠른 탐색능력을 갖는 컨텍스트기반 퍼지 클러스터링을 이용하여 점진적 입자 모델을 설계한다. 이 클러스터링 방법은 출력공간에서 얻어진 컨텍스트로부터 클러스터된 패턴사이의 동질성을 보존함으로써 클러스터들을 생성하도록 사용되어진다. 게다가, 지역적인 밀도지수와 고밀도 포인들로부터의 거리지수의 상관관계를 이용하여 밀도 피크들을 빠르게 탐색하여 각 컨텍스트에 대응하는 타당한 클러스터의 수를 구할 수 있다는 장점을 가지고 있다. 실험은 비선형회귀문제로써 자동차 연료소비량 예측문제를 다루고[10]-[12], 이전 연구된 방법들과 비교하여 우수성과 유용성을 확인하고자 한다.
본 논문의 구성은 다음과 같다. 2절에서는 점진적 입자모델의 구조와 수행절차를 설명하고 있으며, 3절에서는 밀도피크의 빠른 탐색에 근거한 컨텍스트기반 퍼지 클러스터링 방법에 대해서 서술되어진다. 4절에서는 비선형회귀의 실세계응용문제로서 자동차연료소비량 예측문제를 다루며, 마지막으로 5절에서는 결론을 맺는다.
Ⅱ. 점진적 입자모델의 구조와 설계
본 절에서는 선형회귀와 국소 입자모델의 결합한 점진적 입자모델의 구조와 설계방법을 설명한다. 점진적 입자모델의 설계는 두 단계에 의해 이루어진다. 첫 단계는 입출력데이터에 대해서 잘 알려진 선형회귀모델에 의해 예측이 수행된다. 두 번째 단계는 선형회귀에서 얻어진 예측 오차를 제거하기 위해서 퍼지 it-then규칙으로 구성된 지식기반의 국소 입자모델을 설계한다. 여기서 국소 입자모델의 지식생성부분은 다음절에서 자세하게 설명하고자 한다.
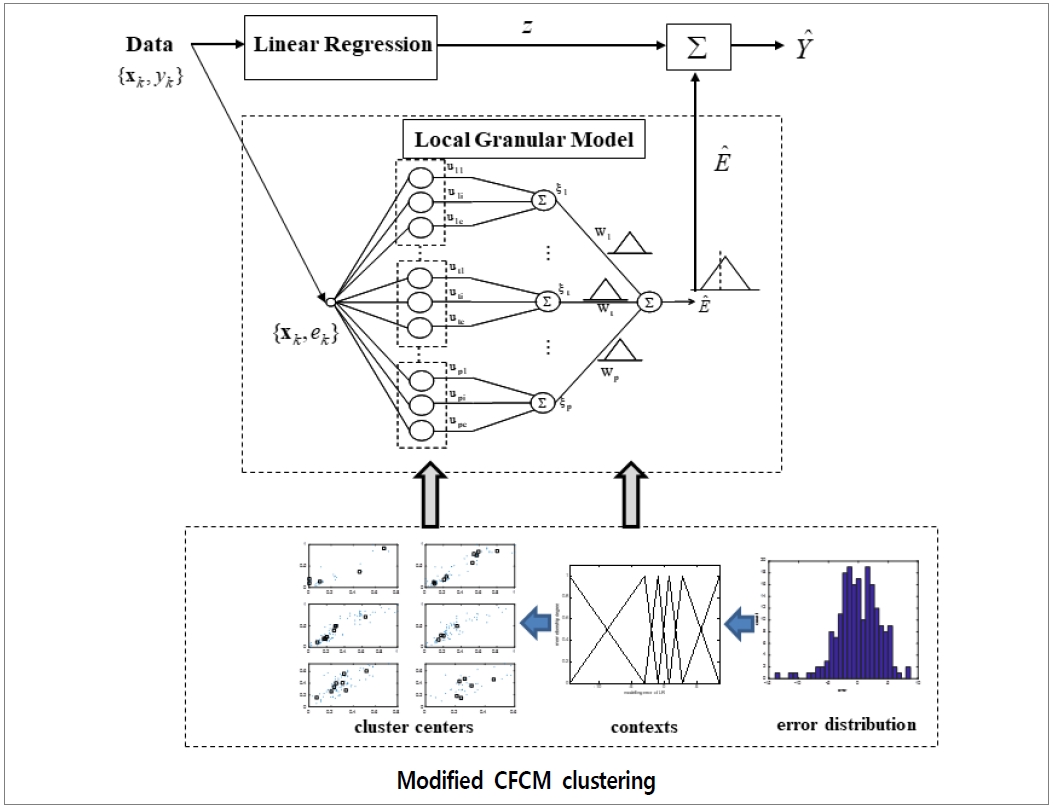
그림 1은 점진적 입자모델의 설계에서 정보처리의 전체적인 흐름도를 보여주고 있다. 그림 1을 단계적으로 설명하면 다음과 같다.
[단계 1] 입출력공간 {xk,yk}에서 전역적인 모델로써 선형회귀(Linear regression)를 이용한다. 여기서 선형회귀에 의해 얻어진 예측오차 정보를 얻고, 입력-오차의 데이터 쌍 {xk,ek}을 형성한다.
[단계 2] 선회회귀 모델의 예측값 z로부터 얻어진 오차공간에서 퍼지집합 형태인 컨텍스트를 생성한다. 여기서 컨텍스트는 확률적인 분포에 의해 간격이 조정되어진다.
[단계 3] 밀도피크의 빠른 탐색에 근거한 개선된 컨텍스트기반 퍼지 클러스터링(CFCM: Context-based Fuzzy C-Means) 방법을 이용하여 각 컨텍스트에 대응하는 클러스터들을 생성하고, 이를 통해 국소 입자모델(Local granular model)이 설계되어진다.
[단계 4] 국소 입자모델에서 은닉층과 출력층간의 가중치는 기존의 수치적인 값이 아닌 오차공간에서 생성되었던 컨텍스트가 가중치 {W1, W2,...,WP}로 사용되어진다. 결과적인 모델의 출력 은 삼각형 소속함수인 퍼지 수로 표현되어진다. 이와 같은 퍼지 수는 상한과 하한경계로 이루어져 출력의 불확실성을 내포하고 있다.
[단계 5] 최종적인 점진적 입자모델의 출력 은 선형회귀의 출력 z와 국소 입자모델의 출력 을 식 (1)과 같이 결합함으로써 계산되어진다.
| (1) |
여기서 대수적인 연산자 ⊕는 최종적인 결과가 퍼지 수에 의해 계산됨을 강조하기 위해서 사용된다.
Ⅲ. 밀도 피크의 빠른 탐색에 근거한 컨텍스트 기반 퍼지 클러스터링
본 절에서는 점진적 입자모델의 설계에서 국소 입자모델을 구축하기 위해서 밀도 피크의 빠른 탐색에 근거한 컨텍스트기반 퍼지 클러스터링에 관해서 설명한다. 기존 연구는 각 컨텍스트에 포함하고 있는 입력데이터 특성을 고려하지 않고 동일한 클러스터의 수가 사용되어지는 문제점을 가지고 있다[6][7]. 이러한 문제를 해결하기 위해 밀도 피크의 빠른 탐색을 이용하여 타당한 클러스터의 수를 구하고자 한다. 이 방법은 클러스터의 수가 직관적으로 추정되어지고 분리되어 있는 포인트는 자동적으로 제외하는 절차에 의해 수행되어진다. 클러스터의 수를 결정하기 위해 지역적인 밀도와 그것의 거리 값들이 계산되어진다. 데이터 포인트 i의 지역적인 밀도 ρi는 식 (2)와 같이 정의되어진다.
| (2) |
여기서 dij는 데이터 포인트 사이의 거리이며, dc는 절단(Cutoff) 거리를 나타낸다. dc는 데이터 집합에서 전체 포인트 수의 1~2%정도 중심 이웃을 만드는 거리행렬에 대한 거리 절단 값을 계산함으로써 얻어진다. 기본적으로, ρi는 포인트 i에 대해서 dc보다 더 가까운 포인트의 수와 같다. 거리 δi는 식 (3)과 같이 고밀도를 가진 다른 포인트와 포인트 i간의 최소 거리를 계산함으로써 얻어진다.
| (3) |
가장 높은 고밀도를 가진 포인트에 대해서, 식 (4)와 같이 정의한다.
| (4) |
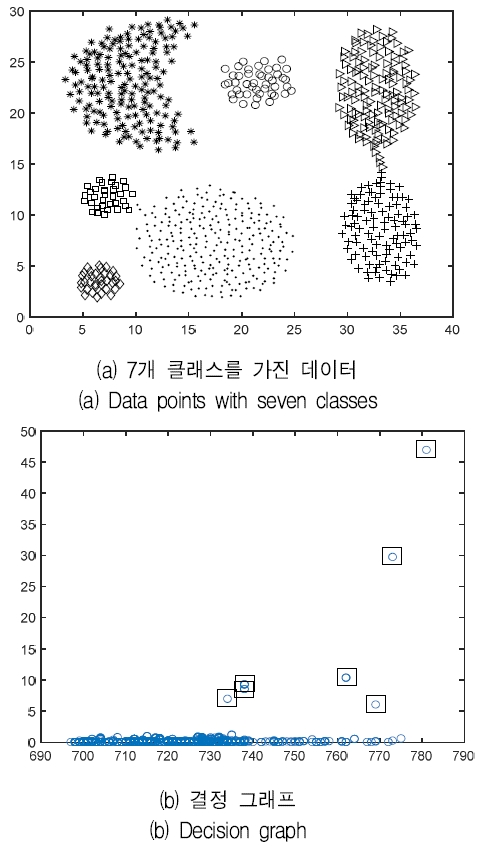
그림 2(a)와 (b)는 각각 7개 클래스를 갖는 합성데이터에 대한 분포와 결정 그래프 결과를 보여준다. 그림 2(b)에서 보는 바와 같이 정확하게 7개의 클래스로 분리한 결과를 확인할 수 있다.
밀도 피크의 빠른 탐색방법에 근거로 해서 소속행렬과 클러스터를 결정하는 알고리즘은 다음과 같은 단계에 의해 수행되어진다.
[단계 1] 출력공간에 생성되는 컨텍스트의 수와 각 컨텍스트에서 추정하고자 하는 클러스터의 수를 정한다. 컨텍스트는 선형회귀로부터 얻어진 예측 오차정보를 가지고 확률적인 분포에 의해 생성된다. 소속행렬은 0과 1사이의 임의의 값을 가지고 초기화되며, 각 컨텍스트에서 추정하고자 하는 클러스터의 수는 밀도피크의 빠른 탐색방법에 근거해서 구해진다.
[단계 2] 각 컨텍스트에서 식 (5)와 같이 클러스터 중심 ci를 계산한다.
| (5) |
| (6) |
여기서 fk는 임의의 컨텍스트에서 k번째 데이터의 소속되는 정도를 나타낸다.
[단계 3] 식 (7)과 같이 목적함수를 계산한다. 현재 값과 이전 값의 차이가 임계치보다 낮다면 멈춘다.
| (7) |
[단계 4] 새로운 소속행렬을 계산하고 [단계 2]로 이동한다.
Ⅳ. 실험결과
본 절에서는 비선형회귀의 실세계 응용문제로서 자동차 연료소비량 예측문제를 다루고자 한다. 자동차 연료소비를 나타내는 MPG(Miles Per Gallon)는 출력변수로 사용되고, 7개의 입력변수(실린더의 수, 무게, 모델연도 등) 가운데 2개의 입력변수를 선택해서 점진적 입자모델을 설계한다. 총 데이터의 수는 392개이며, 각 실험마다 학습과 검증데이터의 비율을 임의선택에 의해 60-40%를 나누고, 10번의 교차 검증 방법을 수행하였다. 이 데이터는 전체 데이터로부터 임의로 선택되어진다. 이렇게 함으로써 결과적인 모델이 학습데이터에 편향되지 않고, 새로운 데이터에 대해서 좋은 일반화 능력을 가질 수 있다. 성능평가는 예측문제에서 일반적으로 사용되는 RMSE(Root Mean Square Error)를 사용하였다[10]-[12]. 간소성을 위해 두 개의 입력변수는 무게와 모델연도를 선택했다[6].
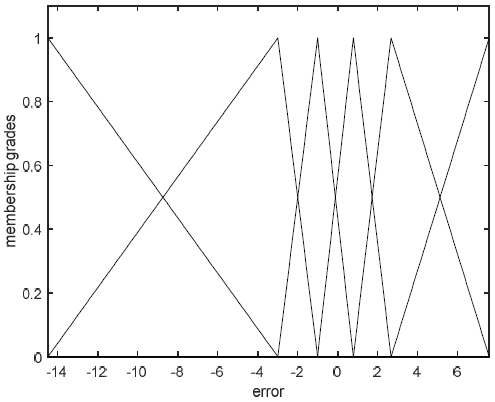
그림 3은 선형회귀로부터 얻어진 예측오차의 확률적인 분포에 의해 생성된 컨텍스트를 보여주고 있다.
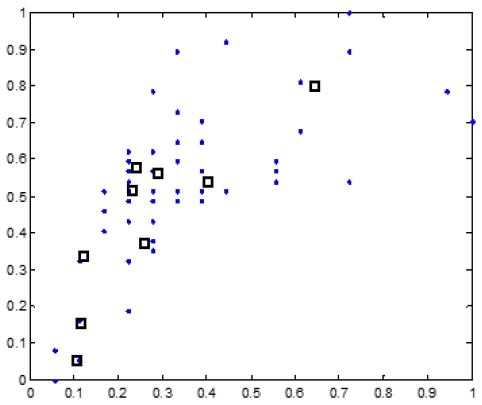
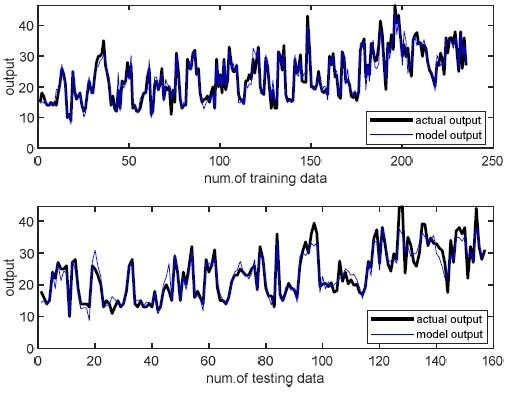
그림 4는 임의의 컨텍스트에 포함된 입력데이터에 대해서 클러스터들을 추정한 결과를 보여주고 있으며, 이들은 데이터 특성을 나타내는 규칙으로써 사용되어진다. 그림 5와 표 1은 학습데이터와 검증데이터에 대해서 각각 예측성능을 보여주고 있다.
그림 5에서 알 수 있는 바와 같이 근사화와 일반화 능력 모두 좋은 성능을 보여주고 있음을 알 수 있었다. 표 1에서 제안된 방법은 컨텍스트 p=6일 때, 각 컨텍스트에 대응하는 클러스터 c=[5 7 8 4 9 9]의 결과를 얻었다.
다시 말하면, 6개의 컨텍스트에서 생성되는 클러스터의 수가 각각 5개, 7개, 8개, 4개, 9개, 9개를 의미한다. 기존방법인 선형회귀, 다층퍼셉트론, 언어적 모델, 개선된 입자모델, 점진적 모델과 비교해서 우수한 성능을 확인할 수 있었다. 이들 비교방법의 구조와 파라미터 설정은 기존논문[10]에서 확인할 수 있다.
Ⅴ. 결 론
본 논문은 선형회귀와 국소 입자모델을 결합한 점진적 입자모델을 설계하기 위해서 수정된 컨텍스트기반 클러스터링방법을 사용한다. 이 클러스터링방법은 밀도피크의 빠른 탐색방법을 이용하기 때문에 각 컨텍스트에서 추정되는 클러스터 수를 자동적으로 얻을 수 있고, 이 클러스터들은 국소 입자모델에서 퍼지 if-then규칙의 지식을 자동적으로 생성할 수 있었다. 자동차 연료소비량 예측문제에 적용한 결과 기존방법과 비교하여 제안된 방법의 유용성과 우수성을 확인할 수 있었다.
차후 국소 입자모델로서 구간형태의 정보입자에 의한 구간기반 점진적 입자모델을 설계하고, 타당한 입자성의 원리에 근거한 새로운 성능지표와 최적화에 관한 연구를 수행할 계획이다.
Acknowledgments
이 논문은 2017학년도 조선대학교 학술연구비의 지원을 받아 연구되었음
References
-
J. T. Yao, A. V. Vasilakos, and W. Pedrycz, "Granular computing: perspectives and challenges", IEEE Transactions on Cybernetics, Vol. 43, No. 6, pp. 1977-1989, Dec. 2013.
[https://doi.org/10.1109/TSMCC.2012.2236648]

-
W. Pedrycz, A. Skowron, and V. Kreinovich, "Handbook of Granular Computing", John Wiley & Sons, 2008.
[https://doi.org/10.1002/9780470724163]

-
X. Zhu, W. Pedrycz, and Z. Li, "Granular models and granular outliers", IEEE Transactions on Fuzzy Systems, Vol. 26, No. 6, pp. 3835-3846, Dec. 2018.
[https://doi.org/10.1109/TFUZZ.2018.2849736]

-
X. Hu, W. Pedrycz, and X. Wang, "Granular fuzzy rule-based models: A study in a comprehensive evaluation and construction of fuzzy models", IEEE Transactions on Fuzzy Systems, Vol. 25, No. 5, pp. 1342-1355, Oct. 2017.
[https://doi.org/10.1109/TFUZZ.2016.2612300]

-
X. Zhu, W. Pedrycz, and Z. Li, "Granular encoders and decoders: A study in processing information granules", IEEE Trans. on Fuzzy Systems, Vol. 25, No. 5, pp. 1115-1126, 2017.
[https://doi.org/10.1109/TFUZZ.2016.2598366]

- M. W. Lee, K. C. Kwak, and W. Pedrycz, "An expansion of local granular models in the design of incremental model", IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, pp. 1664-1670, Jul. 2016.
-
W. Pedrycz and K. C. Kwak, "The development of incremental models", IEEE Transactions on Fuzzy Systems, Vol. 15, No. 3, pp. 507-518, Jun. 2007.
[https://doi.org/10.1109/TFUZZ.2006.889967]

-
D. Shan, W. Lu, and J. Yang, "Interval granular fuzzy models: Concepts and Development", Institute of Electrical and Electronics Engineers, Vol. 7, pp. 24140-24152, Feb. 2019.
[https://doi.org/10.1109/ACCESS.2019.2899830]

-
A. Rodriguez and A. Laio, "Clustering by fast search and find of density peaks", Science, Vol. 344, No. 6191, pp. 1492-1496, Jun. 2014.
[https://doi.org/10.1126/science.1242072]

-
K. C. Kwak, "A design of granular model using conditional clustering and density peaks", Journal of KIIT, Vol. 13, No. 7, pp. 127-134, Jul. 2015.
[https://doi.org/10.14801/jkiit.2015.13.7.127]

-
C. U. Yeom and K. C. Kwak, "Performance evaluation of automobile fuel consumption using a fuzzy-based granular model with coverage and specificity", Symmetry, Vol. 11, No. 12, Dec. 2019.
[https://doi.org/10.3390/sym11121480]

-
W. Pedrycz and A. V. Vasilakos, "Linguistic models and linguistic modeling", IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), Vol. 29, No. 6, pp. 745-757, Dec. 1999.
[https://doi.org/10.1109/3477.809029]


2016년 2월 : 조선대학교 제어계측로봇공학과(학사)
2017년 8월 : 조선대학교 제어계측공학과(석사)
2017년 9월 ~ 현재 : 조선대학교 제어계측공학과 박사과정
관심분야 : 입자 컴퓨팅, 계산지능

2002년 : 충북대학교 전기공학과 박사 졸업
2003년 ~ 2005년 : 캐나다 앨버타대학교 전기 및 컴퓨터 공학과, 박사후과정
2005년 ~ 2007년 : 한국전자통신 연구원 지능형로봇연구단 선임연구원
2014년 ~ 2015년 : 미국 캘리포니아 주립대학교 플러튼, 방문교수
2007년 ~ 현재 : 조선대학교 전자공학부 교수
관심분야 : 계산지능, 인간-로봇상호작용, 바이오인식