위상배열안테나 시스템의 패턴 널 형성 기법에 관한 연구

Ⅰ. 서 론

무선 통신망은 타 통신 채널(Channel)의 간섭 혹은 재밍(Jamming) 신호원에 의해 통신 품질 저하 현상이 발생할 수 있다. 이와 같은 환경에서 통신망을 유지함과 동시에 간섭원의 영향을 줄이기 위한 근본적인 방법은 통신용 안테나의 주 빔(Main lobe)는 대국을 지향함과 동시에 신호 간섭원 방향으로는 패턴 널(Pattern null)을 형성하는 것이다[1]-[3].

상기와 같은 방사 특성(Radiation characteristics)을 유도하기 위해서는 안테나의 빔을 조향 및 형성할 수 있어야 한다. 위상배열안테나 시스템은 각 방사 소자(Radiating element)에 급전되는 신호의 위상을 가중 천이하여 전기적으로 빔을 조향 및 형성할 수 있다[4]. 따라서 위상배열안테나 시스템은 상기와 같은 문제의 해소가 필요한 통신망에서 많이 사용된다.

위상배열안테나 시스템에 있어, 요구 빔 조향 각도 및 패턴 널 각도에 대응한 빔을 형성하기 위해서는 최적의 위상천이 가중벡터(Phase shifting weighting vector)를 탐색해야 한다. 일반적으로 주 빔만을 형성하는 경우의 위상천이 가중벡터는 위상배열안테나 관련 수식을 이용하여 쉽게 산출할 수 있으나, 주 빔의 형성과 동시에 특정 방향으로 패턴 널을 형성하기 위한 위상천이 가중벡터의 산출은 수식으로 접근하기 어렵다. 따라서 주 빔의 형성과 동시에 패턴 널을 형성하기 위한 최적의 위상천이 가중벡터 탐색하는 문제는 수많은 경우의 수 중 근사해를 찾아야 하는 문제로 대응되고, 이는 NP-완전 문제의 영역에 해당한다. (여기서 경우의 수는 방사 소자 배열 수가 증가할수록 증가한다.)

NP-완전 문제는 휴리스틱 알고리즘(Heuristic algorithm)을 이용하여 효율적으로 해소할 수 있다. 따라서 휴리스틱 알고리즘을 이용하여 주 빔과 패턴 널을 동시에 형성할 수 있는 위상천이 가중벡터 탐색에 관한 연구가 많이 진행되어 왔다[3][5]-[7]. 그러나 기존 연구의 경우, 위상천이 가중벡터 탐색을 위한 알고리즘 수행 초기에 주 빔의 이득이 감소하는 현상이 발생한다. 이는 패턴 널을 형성하는 과정에서 대국과의 통신이 간헐적으로 단절될 수 있음을 뜻한다.

본 논문에서는 원활한 통신망 구축과 함께 간섭원의 신호를 억제하기 위해 대국과의 통신을 위한 주 빔은 유지하면서, 동시에 패턴 널을 형성할 방법을 제안하였다. 이를 위해 위상배열안테나의 양자화 위상천이 오차에 따른 빔 조향 오차를 산출하는 연구 결과[8]를 기반으로, 특정 빔 조향 오차를 일으키는 새로운 위상천이 가변 범위를 산출하였다. 그리고 상기 위상천이 가변 범위를 기준으로 패턴 널 합성을 위한 휴리스틱 알고리즘을 수행하였다. 이에 따라 주 빔을 유지함과 동시에 패턴 널을 형성할 수 있음을 확인하였다.

Ⅱ. 위상천이 가중벡터 탐색 설정

2.1 위상배열안테나

본 논문에서는 위상배열안테나의 구성을 x 축에 선형, 등 간격 그리고 균등 급전되었다고 가정하였다. 위상배열안테나의 방사특성은 일반적으로 AF (Array Factor)를 기반으로 분석한다. 식 (1)은 상기 가정에 따른 위상배열안테나의 AF를 보여준다.

$\[ AF=\frac{1}{N}\sum _{n=1}^N{e}^{jkd\left(n-1\right)\sin \theta +j{\alpha }_n} \]$

(1)

여기서 k는 전파 상수, d는 등간격으로 배열된 방사 소자 간 간격 그리고 n은 n 번째 방사 소자를 뜻한다. α_n 은 위상배열안테나의 전기적 빔 형성을 위한 n번째 방사 소자의 위상천이 가중값이다.

위상천이 가중벡터는 요구 빔 조향 각도(θ_d)에서 식 (1)이 1이 되면 된다. 따라서 요구 빔 조향 각도에 주 빔만을 형성하기 위한 각 방사 소자의 위상천이 가중값은 식 (2)와 같이 된다.

$\[ {\alpha }_n=-kd\left(n-1\right)\sin {\theta }_d \]$

(2)

위상배열안테나의 위상천이를 위한 위상천이기는 일반적으로 디지털 위상천이기가 사용된다. 이에 따라 식 (2)의 위상천이 가중값은 디지털 위상천이기의 분해능에 따라 양자화된다.

식 (3)은 식 (2)를 위상천이기 분해능으로 양자화하였을 때의 값을 보여준다.

$\[ {\alpha }_n^Q=res\left[\partial \left({\alpha }_n/res\right)\right] \]$

(3)

여기서 res는 디지털 위상천이기의 분해능이고, ∂는 반올림 연산 함수이다.

주 빔만을 형성하기 위해서는 식 (3)을 이용하면 된다. 그러나 주 빔과 동시에 패턴 널을 합성하기 위해서는 수식을 이용하여 쉽게 산출할 수 없다. 따라서 다양한 방법을 통해 최적의 위상천이 가중벡터(α_n) 조합을 탐색해야 한다.

본 논문에서는 모의실험을 통해 패턴 널 형성 기법에 관하여 분석하였다. 이를 위한 위상배열안테나의 기본 구성 조건을 표 1과 같이 설정하였다.

Table 1.

Parameter setting for phased array antenna

2.2 휴리스틱 알고리즘 설정

주 빔과 함께 패턴 널을 형성하기 위한 위상천이 가중벡터는 식 (3)과 같이 쉽게 산출되지 않는다. 더불어 방사 소자 배열 수에 따라 벡터의 차원이 증가하기 때문이다. 이는 NP-완전 문제에 대응된다. 휴리스틱 알고리즘을 이용하면 NP-완전 문제를 효율적으로 근사해를 구할 수 있다. 따라서 본 논문에서는 패턴 널 기법을 분석하기 위해 휴리스틱 알고리즘을 이용하였다. 대표적인 휴리스틱 알고리즘으로 유전 알고리즘(GA, Ggenetic Algorithm), 입자 군집 최적화(PSO, Particle Swarm Optimization) 그리고 포복경 영양 번식(VPR, Vegetative Propagation by Runner) 알고리즘이 있다[9]-[11].

이중 VPR 알고리즘은 휴리스틱 알고리즘이 가지고 있는 지역 수렴(Local optima) 문제를 효율적으로 해소할 수 있는 알고리즘으로 연구되었다. 따라서 본 논문에서는 VPR 알고리즘을 이용하였다.

VPR 알고리즘은 식 (4)와 같이 각 식물의 주근 및 부근을 통해 획득한 토양 비용 평갓값(P_b, S_b)을 기반으로 산출된 포복경의 위치를 기반으로 최고 토양 위치를 탐색 번식하는 알고리즘이다.

$\[ Ru{n}^i=C_{r}r\left(\right)\left(S_b^i-X^i\right)+C_{p}r\left(\right)\left(P_b-X^i\right) \]$

(4)

여기서 i는 i번째 식물, Run은 포복경 위치, r()은 난수 발생함수, C_p와 C_r은 주근 및 부근에 의한 포복경 생성 계수 그리고 Xⁱ는 i번째 식물의 현재 위치이다.

주근은 식물의 위치(Xⁱ)에 형성되며, 부근은 주근 인근에 형성된다. 이에 따라 부근의 위치는 정규분포 난수 함수(randn())를 사용하여 식 (5)와 같이 표현된다.

$\[ R^i\left(m,:\right)=X\left(i,:\right)+C_{s}randn\left(\right) \]$

(5)

여기서 Rⁱ(m,:)는 i번째 식물의 m번째 위치이고, C_s 는 부근 위치 발생 계수이다.

식 (4)를 기반으로 생성된 포복경에 의한 다음 세대 식물의 위치는 식 (6)과 같이 산출된다.

$\[ X^i\left[t+1\right]=X^i\left[t\right]+Ru{n}^i \]$

(6)

여기서 t는 세대(알고리즘 수행 횟수)를 뜻한다.

VPR 알고리즘은 식물의 노화를 모사하여, 지역 수렴 현상을 개선하였다. 식물의 노화는 식 (7)과 같이 세대(t)에 비례하여 증가하는 ‘※’ 변수를 이용하였다. 여기서 ‘※’는 식물에 의해 탐지된 최고 비용 평갓값(P_b)이 갱신되면, 0으로 초기화된다.

$\[ P_b^{\cos t}=P_b^{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-C_{t}att\right) \]$

(7)

여기서 C_t는 식물 노화 계수이다.

각 식물의 위치(Xⁱ)는 본 논문에서 탐색하고자 하는 위상천이 가중벡터 조합(α_n)에 대응된다.

표 2는 위상천이 가중벡터 탐색을 위한 VPR 알고리즘의 설정값을 보여준다.

Table 2.

Parameter setting for VPR algorithm

Ⅲ. 기존 패턴 널 형성 기법

기존 패턴 널 형성 기법은 휴리스틱 알고리즘을 이용하여 요구 빔 조향 각도에 주 빔을 형성하고 간섭원 각도에 패턴 널을 형성하기 위한 각 방사 소자의 위상천이 가중값을 [0,2π) 범위 내에서 탐색하는 방법이다. 이는 가용한 모든 범위 내에서 위상천이 가중벡터 조합을 탐색하는 것을 뜻한다.

본 절에서는 기존 패턴 널 합성 기법의 모의실험을 통해 문제점을 확인하였다.

3.1 모의실험 조건

휴리스틱 알고리즘은 난수를 기반으로 하여 근사해를 탐색한다. 따라서 분석을 위해서는 다수의 모의실험을 통해 얻은 알고리즘 종료 결과를 기반으로 평균 종료 횟수를 기준으로 분석되어야 한다. 이를 위해 모의실험을 1000회 수행하였다.

여기서 모의실험을 위한 위상배열안테나 및 VPR 알고리즘의 기본 조건은 표 1과 2와 같다. 그리고 VPR 알고리즘을 이용하여 근사해를 탐색하기 위한 비용 평가값은 식 (8)과 같이 설정하였다.

$\[ \cos t=\left[\left|AF\left({\theta }_n\right)\right|+1/AF\left({\theta }_d\right)\right] \]$

(8)

여기서 AF(θ_d)와 AF(θ_n)은 요구 빔 조향 각도 및 패턴 널 각도에서의 AF 값이다. 따라서 휴리스틱 알고리즘은 비용 평갓값이 최소가 되도록 위상천이 가중벡터를 탐색하게 된다.

휴리스틱 알고리즘의 종료 조건은 식 (9)가 동시에 만족할 때로 설정하였다.

$\[ 20{\log }_{10}\left[AF\left({\theta }_d\right)\right] \geqq 0.4 \left[dB\right] \]$

(9-1)

$\[ 20{\log }_{10}\left[AF\left({\theta }_n\right)\right] \leqq -50 \left[dB\right] \]$

(9-2)

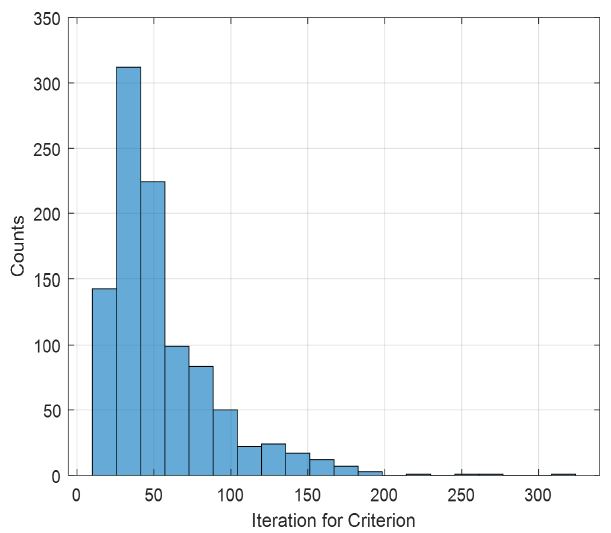
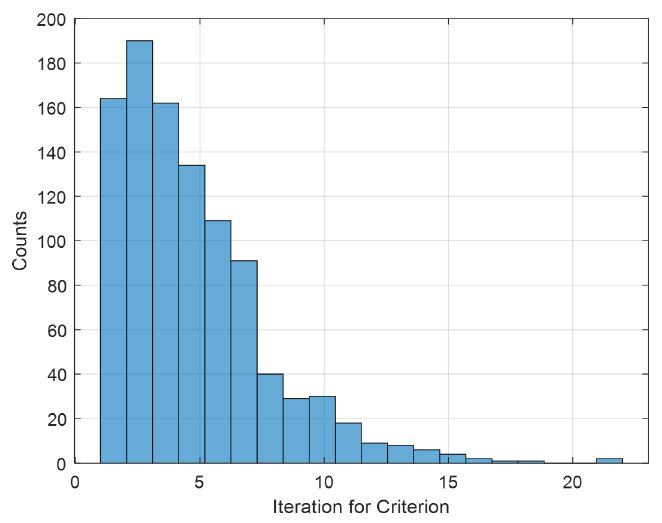
그림 1은 모의실험을 1000회 수행하였을 때, 식 (9)의 알고리즘 종료 조건을 만족한 알고리즘 수행 횟수의 분포를 보여준다.

Fig. 1.

Histogram result for conventional method

분석 결과 기존 패턴 널 형성 방법의 평균 알고리즘 종료 횟수는 55.07이다. 이에 패턴 널 형성에 관한 상세한 분석은 알고리즘 종료 횟수가 55회인 경우를 기준으로 정하였다.

3.2 상세 분석

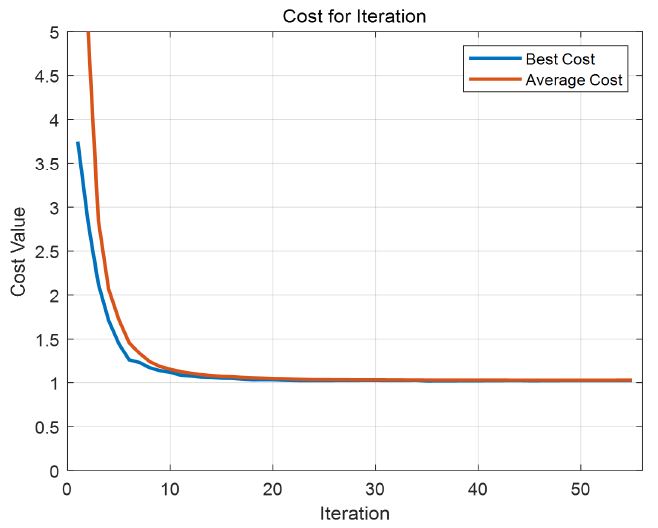
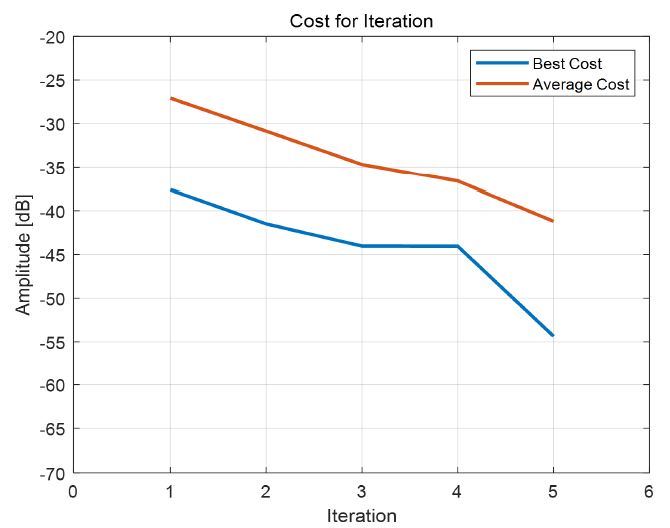
그림 2는 VPR 알고리즘 종료 횟수가 55인 경우의 식 (8)에 의해 산출된 식물군 최고 비용 평가값과 평균 비용 평가값을 보여준다.

Fig. 2.

Best and average cost value

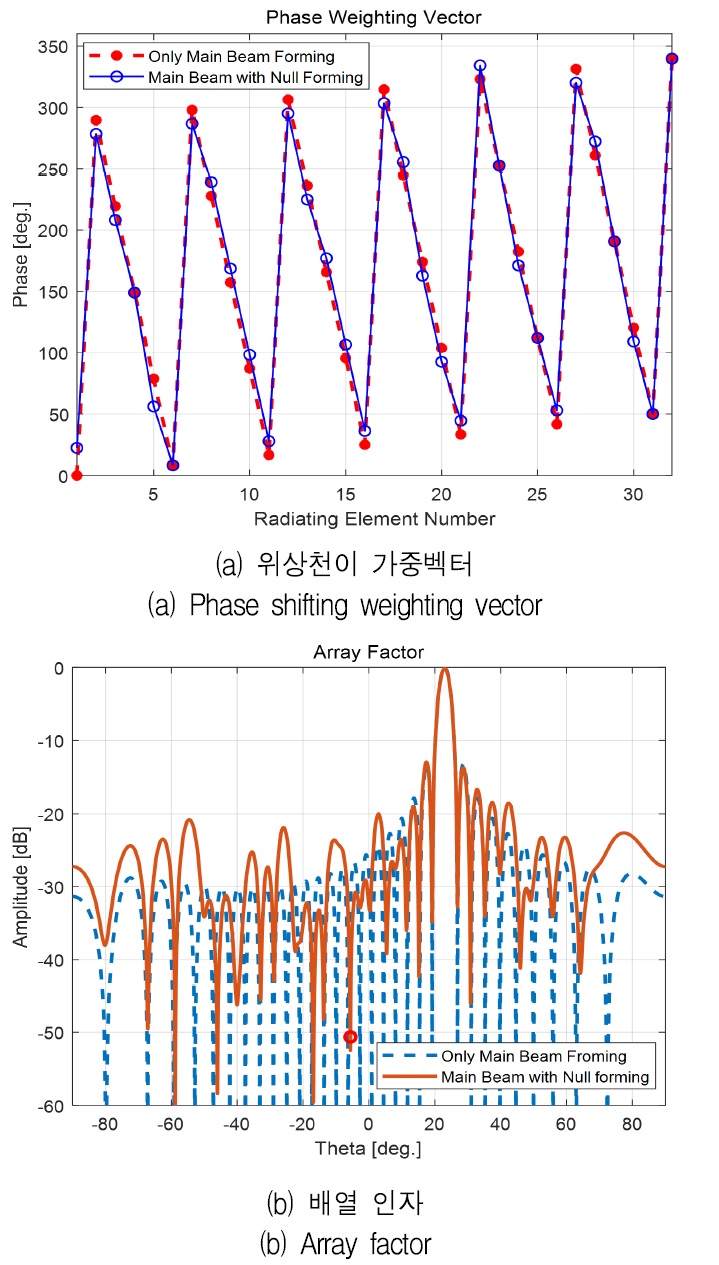
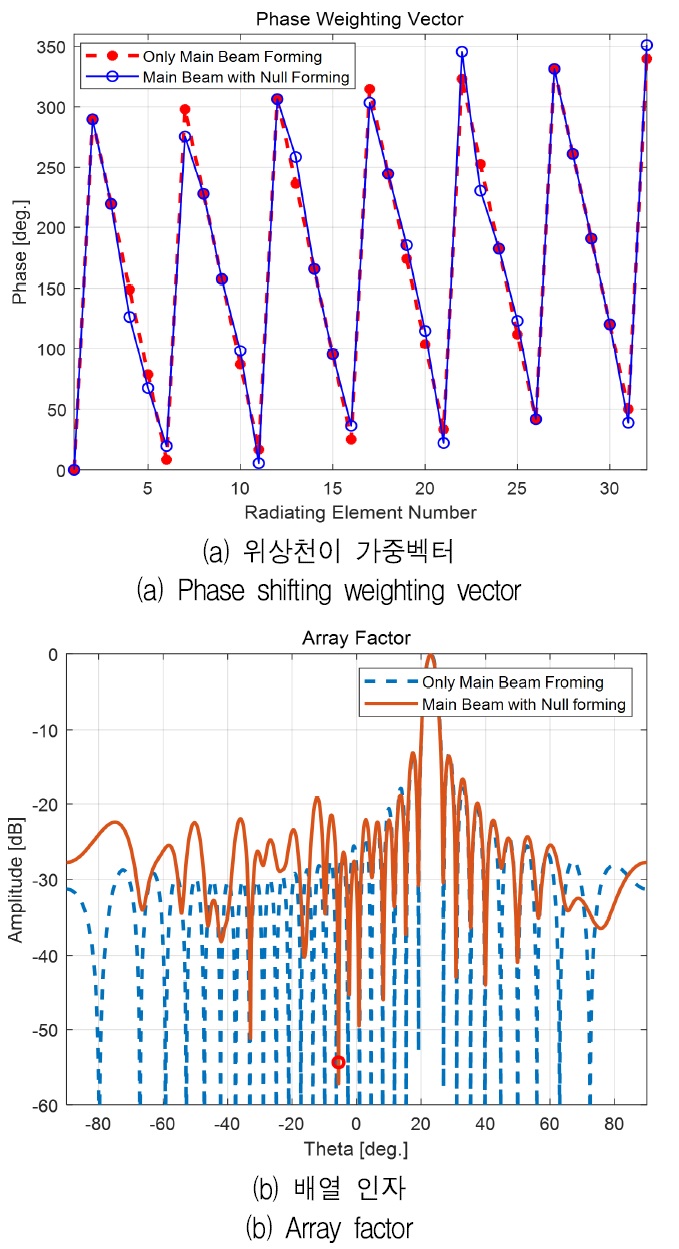
그림 3은 VPR 알고리즘 종료에 따라 최종적으로 탐색 된 위상천이 가중벡터와 AF를 보여준다. 그림 3은 식 (2) 및 (3)에 의해 산출된 주 빔만 형성하는 위상천이 가중벡터 조합과 비교 도시하였다.

Fig. 3.

Phase shifting weighting vector and AF

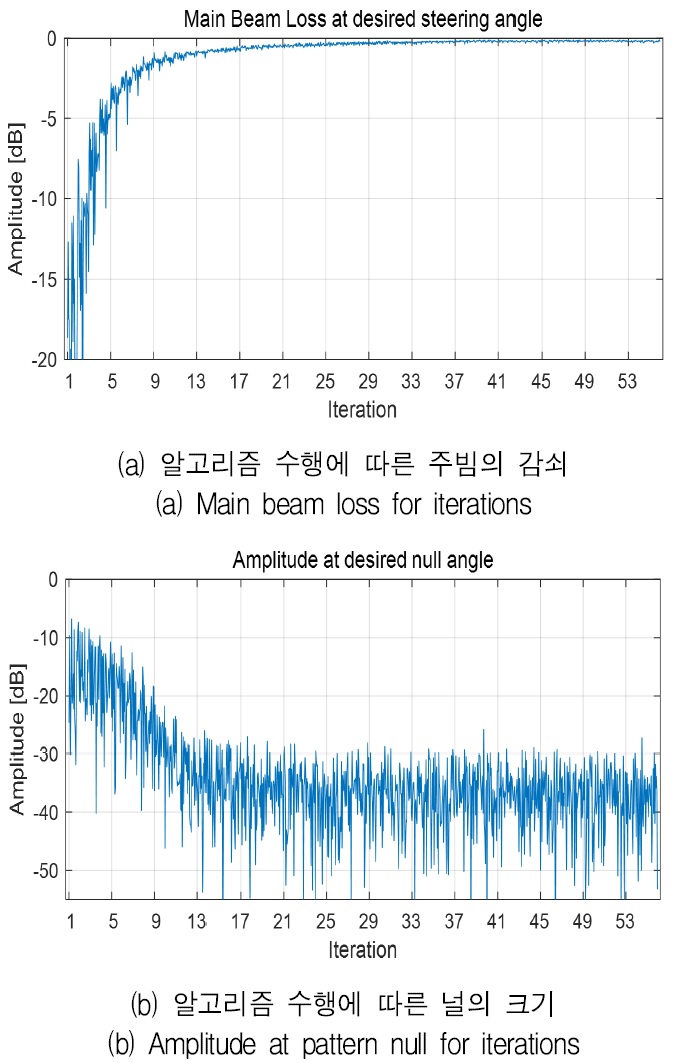
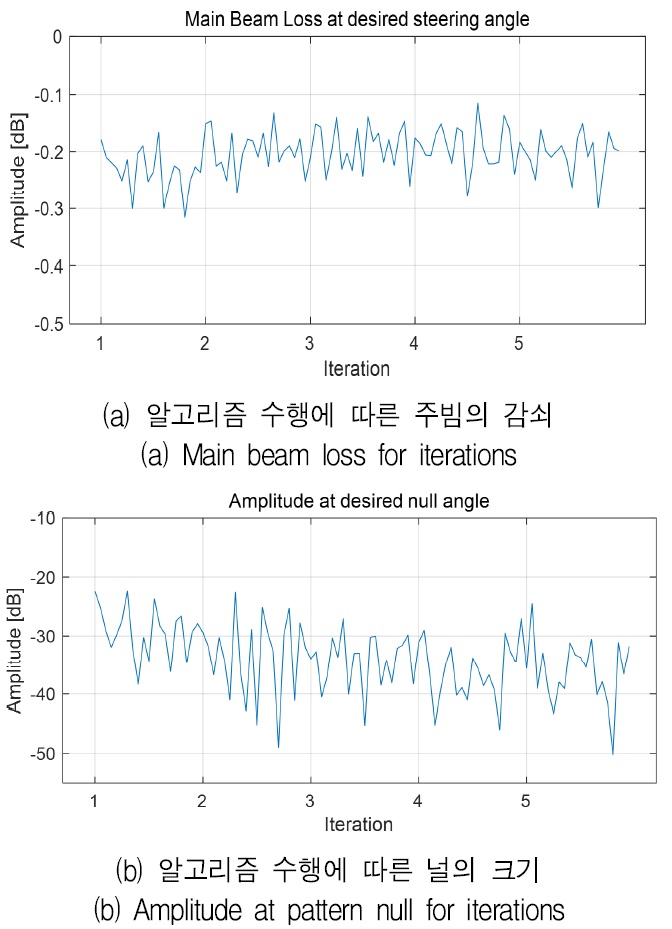
그림 4는 알고리즘 수행에 따른 세대별, 각 식물의 AF(θ_d)와 AF(θ_n)의 20log₁₀을 취한 값을 보여준다.

Fig. 4.

AF amplitude according to algorithm

그림 3에서 확인할 수 있듯이, 요구 조건에 맞게 최종 빔이 잘 형성되었음을 알 수 있다. 그러나 그림 4에서 확인할 수 있듯이, 알고리즘 수행 초기에 주 빔의 이득이 낮아짐을 알 수 있다. 이는 기존 패턴 널 형성 기법의 경우, 요구 조건에 맞는 위상천이 가중벡터의 근사해를 탐색하기 위해 위상천이기의 가용 범위 전체를 탐색하기 때문이다. 분석 결과 알고리즘 수행 횟수에 따라 주 빔의 이득 손실은 최대 –36.673dB에서 –0.088dB 사이에서 변화하였으며, 요구 패턴 널 각도에서의 크기는 –63.648dB에서 –8.982dB 사이에서 변화하였다.

결과적으로 기존 패턴 널 형성 기법을 적용하여 주 빔과 동시에 패턴 널을 형성하면, 알고리즘 수행 초기에 대국과의 통신이 단절되는 현상이 발생한다.

Ⅳ. 제안된 패턴 널 형성 기법

본 논문에서는 기존 패턴 널 형성 기법에서 발생하는 알고리즘 수행 초반, 주 빔의 이득 감소 현상을 개선하기 위해 알고리즘 수행 중, 주 빔은 지속해서 유지함과 동시에 패턴 널을 형성하는 기법을 제안하였다. 제안된 방법을 적용하기 위해 탐색하고자 하는 위상천이 가중벡터를 식 (10)과 같이 변경하였다.

여기서 α_n은 패턴 널 합성하기 전, 주 빔만을 형성하기 위해 식 (2)와 (3)에 의해 산출된 위상천이 가중벡터이고, β_n은 패턴 널을 형성하기 위해 변화 범위가 제한된 위상천이 가중벡터이다. 이에 따른 AF는 식 (11)과 같이 변경된다.

알고리즘 수행과정 중, 주 빔을 유지하면서 패턴 널을 형성하기 위한 β_n의 변화 범위는 위상천이기의 양자화 오차에 따른 주 빔의 빔 조향 오차에 관한 연구의 결과를 이용하여 유도하였다. 식 (12)은 상기 연구에 따른 평균 양자화 위상 오차에 따른 빔 조향 오차 각도 산출 식이다[8].

여기서 θ_e는 빔 조향 오차, asin은 sin의 역함수 그리고 e_aυ는 디지털 위상천이기에 의한 평균 양자화 오차이다.

이를 역으로 산출하면, 주 빔의 최대 빔 조향 오차 각도에 대응하는 평균 양자화 위상천이 값을 산출할 수 있다. 이에 따른 e_aυ는 식 (13)와 같다.

식 (13)에 의해, 주 빔의 최대 빔 조향 오차(θ_e)에 따른 e_aυ는 평균 위상천이 오차이다. 양자화 위상천이 평균 오차는 최대 양자화 오차의 0.25배이므로, 최대 위상천이 오차 범위는 [-2e_aυ,2e_aυ]가 된다. 본 논문에서는 상기 범위를 새로운 위상천이 가중벡터의(β_n) 탐색 범위로 설정하였다. 이에 따라 패턴 널 합성을 위해 β_n이 VPR 알고리즘에 의해 탐색 되는 동안 α_n에 의해 설정된 주 빔은 θ_e의 범위 내에서만 변하게 된다.

4.1 모의실험 조건

모의실험을 위한 기본 설정은 표 1과 표 2에 기술된 내용과 같다. 제안된 기법에 추가된 내용을 적용하기 위한 주 빔의 최대 빔 조향 오차 각도(θ_e)는 표 1의 구성을 가지는 위상배열안테나에 있어, 요구 빔 조향 각도(θ_d)가 0deg.인 경우의 반치각(HPBW, Half Power Beam Width)의 1/4배로 설정하였다. 이에 따른 θ_e는 약 0.4deg.이다. 상기 최대 조건에 따른 β_n의 최대 변화 범위는 [-24.291deg., 24.291deg.]이고, 이 값을 표 1의 디지털 위상천이기의 분해능으로 양자화하면 [-22.5deg., 22.5deg.]가 된다.

상기와 같은 설정을 기반으로 상세 분석을 위한 평균 알고리즘 종료 횟수를 확인하기 위해 VPR 알고리즘을 1000회 수행하였다. 여기서 근사해 탐색을 위한 비용 평갓값은 식 (14)와 같이 설정하고, 알고리즘 종료 조건은 식 (9-2)와 같이 설정하였다.

$\[ \cos t=20{\log }_{10}\left[AF\left({\theta }_n\right)\right] \]$

(14)

3장과 다르게, 패턴 널만의 AF 값을 평가하는 이유는 주 빔은 ±0.4deg. 범위 내의 오차만 발생하기 때문이다.

그림 5는 모의실험을 1000회 수행하였을 때, 식 (9-2)의 알고리즘 종료 조건을 만족한 알고리즘 수행 횟수의 분포를 보여준다.

Fig. 5.

Histogram result for proposed method

분석 결과 제안된 패턴 널 형성 방법의 평균 알고리즘 종료 횟수는 5.003이다. 이에 패턴 널 형성에 관한 상세한 분석은 알고리즘 종료 횟수가 5회인 경우를 기준으로 정하였다.

4.2 상세 분석

그림 6은 VPR 알고리즘 종료 횟수가 5인 경우의 식 (13)에 의해 산출된 식물군 최고 비용 평갓값과 평균 비용 평갓값을 보여준다.

Fig. 6.

Best and average cost value

그림 7은 VPR 알고리즘 종료에 따라 최종적으로 탐색 된 위상천이 가중벡터와 AF를 보여준다. 여기서 위상천이 가중벡터는 식 (10)의 결과이다. 그림 7은 식 (2) 및 식 (3)에 의해 산출된 주 빔만 형성하는 위상천이 가중벡터 조합과 비교 도시하였다. 모의실험 결과 가용 범위 [-22.5deg. 22.5deg.]의 β_n만으로도 요구 빔 조향 각도(θ_d)와 요구 패턴 널 각도(θ_n)에 맞게 빔이 형성되었음을 알 수 있다.

Fig. 7.

Phase set and AF

그림 8은 알고리즘 수행에 따른 세대별, 각 식물의 AF(θ_d)와 AF(θ_n)의 20log₁₀을 취한 값을 보여준다. 결과에서 확인할 수 있듯이, VPR 알고리즘 수행에 따라 주 빔의 이득이 유지됨을 알 수 있다.

Fig. 8.

AF according to algorithm

분석 결과 본 논문에서 제안된 방법을 이용하여 패턴 널을 합성하면 주 빔의 변화가 미미하므로 안정적으로 대국과의 무선 통신망을 유지함과 동시에 간섭원에 대한 패턴 널을 형성할 수 있음을 알 수 있다.

분석 결과 알고리즘 수행 횟수에 따라 주 빔의 이득 손실은 최대 –0.3675dB에서 –0.119dB 사이에서 변화하였으며, 요구 패턴 널 각도에서의 크기는 -51.072dB에서 -20.8764dB 사이에서 변화하였다.

더불어 그림 1과 그림 5의 결과를 비교하였을 때, 같은 조건의 VPR 알고리즘을 사용하였음에도 본 논문에서 제안한 방법의 경우 평균 알고리즘 종료 횟수가 5회로 기존 방법(55회)보다 매우 빠르게 패턴 널을 형성할 수 있음을 알 수 있다.

그러나 본 논문에서 제안한 방법은 휴리스틱 알고리즘에 의해 탐색하고자 하는 위상천이 가중벡터의 범위가 제한적이다. 이에 표 1에 기술되어 있는 요구 패턴 널 각도 이외의 값에서도 패턴 널이 잘 형성될 수 있음을 확인해야 한다.

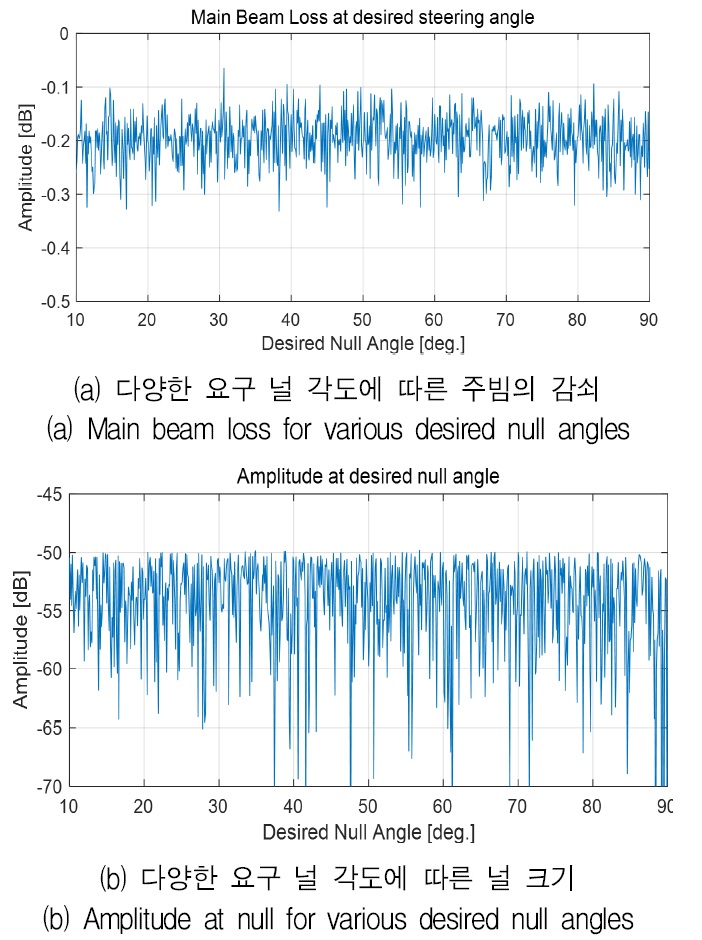
이를 위해 요구 빔 조향 각도(θ_d)가 0deg.이고, 요구 패턴 널 각도(θ_n)가 10deg.에서 90deg.까지 0.1deg.로 변화하는 경우에 대하여 분석하였다. 그림 9는 상기 조건에 따른 위상배열안테나에 있어, VPR 알고리즘에 의해 탐색 된 최종 위상천이 가중벡터 조합에 의한 AF(θ_d)와 AF(θ_n)에 20log₁₀을 취한 값을 보여준다.

Fig. 9.

Simulated results for desired null angles

분석 결과 요구 패턴 널 각도에 –50dB 이상의 널이 형성되었음을 알 수 있다. 이와 동시에 주 빔의 최소 및 최대 이득 손실은 각각 –0.342dB와 -0.0936dB이고, 평균 이득 손실은 –0.198dB로 확인되었다.

모의실험 분석 결과 제안된 패턴 널 합성 기법은 다양한 요구 패턴 널 각도에서도 성능을 확보할 수 있음을 알 수 있다.

Ⅴ. 결 론

본 논문에서는 위상배열안테나 시스템에 있어, 주 빔에 의한 통신망이 구축된 상황에서 간섭원이 발생하였을 때, 간섭원에 대한 근본적인 해소를 위한 패턴 널 형성 기법에 관하여 연구하였다. 패턴 널 합성을 위해 휴리스틱 알고리즘이 동작할 경우, 주 빔의 변화 범위를 제한할 수 있는 위상천이 가중벡터의 가변 범위를 유도하고, 이를 통해 주 빔에 대한 미미한 변화와 함께 패턴 널을 형성할 수 있음을 확인하였다. 본 논문에서 제안된 방법은 패턴 널 합성 이외에도 위상배열안테나 시스템의 부엽(Side lobe) 제어에도 적용할 수 있을 것으로 판단된다.

References

• Kai-Bor Yu, "Adaptive beamforming for satellite communication with selective earth coverage and jammer nulling capability", IEEE Transactions On Signal Processing, Vol. 44, No. 12, pp. 3162-3166, Dec. 1996. [https://doi.org/10.1109/78.553494]
• S. W. Choi and D. H. Shim, "A novel adaptive beamforming algorithm for a smart antenna system in a CDMA mobile communication environment", IEEE Transaction on Vehicular Technology, Vol. 49, No. 5, pp. 1793-1806, Sep. 2000. [https://doi.org/10.1109/25.892584]
• R. L. Haupt, "Phase-Only adaptive nulling with genetic algorithm", IEEE Transaction on Antennas Propagation, Vol. 45, No. 5, pp. 1009-1015, Jun. 1997. [https://doi.org/10.1109/8.585749]
• J. W. Jung, J. H. Ryu, T. H. Joo, K. C. Kim, I. H. Park, and J. W. Seo, "Design of Conformal Active Phased Array Antenna for communications", Magazine of the IEEK, Vol. 44, No. 4, pp. 39-47, Apr. 2017.
• M. M. Khodier and C. G. Christodoulou, "Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization", IEEE Transactions on Antennas and Propagation, Vol. 8, No. 53, pp. 5674-2679, Aug. 2005. [https://doi.org/10.1109/TAP.2005.851762]
• R. M. Davis, "Phase-only LMS and perturbation adaptive algorithms", IEEE Transactions on Aerospace and Electronic Systems, Vol. 34, No. 1, pp. 169-178, Jan. 1998. [https://doi.org/10.1109/7.640274]
• M.. Fakharzadeh, Safavi-Naeini, S. H. Jamali, and P. Mousavi, "Zero-knowledge beamforming of Phased array antennas based on simultaneous perturbation gradient approximation", IEEE Int. Symp. Antennas Propagation, Albuquerque, NM, pp. 537-540, Jul. 2006. [https://doi.org/10.1109/APS.2006.1710578]
• J. W. Jung, Y. D. Kim, and J. W. Seo, "A Study on beam pointing error according to resolution of phase shifter for phased array antenna", J. of The Institute of Electronics and Information Engineers, Vol. 57, No. 1, Jan. 2020. (will be published) [https://doi.org/10.5573/ieie.2020.57.1.42]
• L. Davis, Ed., "Handbook of Genetic Algorithms. Van Nostrand Reinhold", New York, NY, 1991.
• J. Kennedy and R. Eberhart, "Particle swarm optimization", Proc. IEEE International Conf. on Neural Networks (Perth, Australia), IEEE Service Center, Piscataway, NJ, 1995.
• J. W. Jung, "Vegetative Propagation by Runners Optimization Algorithm", Journal of The Institute of Electronics and Information Engineers, Vol. 55, No. 9, pp. 25-31, Sept. 2018. [https://doi.org/10.5573/ieie.2018.55.9.25]