[ Article ]

The Journal of Korean Institute of Information Technology - Vol. 17, No. 12, pp.55-62

ISSN: 1598-8619 (Print) 2093-7571 (Online)

Print publication date 31 Dec 2019

Received 26 Sep 2019 Revised 07 Oct 2019 Accepted 10 Oct 2019

DOI: https://doi.org/10.14801/jkiit.2019.17.12.55

다중 사용자 대용량 MISO 시스템에서 전력 전송을 위한 하이브리드 프리코더 설계 기법

서방원^*

*공주대학교 전기전자제어공학부 (IT융합기술연구소) 부교수

Hybrid Precoder Design Scheme for Power Transfer in Multiuser Massive MISO Systems

Bangwon Seo^*

Correspondence to: Bangwon Seo Dept. of Electrical, Electronics and Control Engineering, the Institute of IT Convergence Technology (IITC), Kongju National University, Cheonan, Korea, Tel.: +82-41-521-9178, Email: seobw@kongju.ac.kr

초록

본 논문은 정보 데이터와 전력을 동시에 전송하는 대용량 다중 사용자 다중 입력 단일 출력 (MISO) 시스템에서, 고주파 대역 신호처리 체인의 개수가 송신 안테나의 개수보다 적은 경우에 대한 하이브리드 프리코더 및 전력 분배 상수를 설계하는 기법을 제안한다. 기존의 송신단 ZF 프리코딩 기법은 부가잡음을 고려하지 않는다는 문제점을 보완하기 위하여, 제안하는 기법에서는 신호대 누수 잡음비 (SLNR)를 비용 함수로 사용한다. 따라서, 수확 가능 전력에 대한 최소값을 만족시킨다는 제약 조건 하에서, SLNR 비용함수를 최대화시키도록 하이브리드 프리코딩 벡터와 전력 분배 상수를 설계한다. 제안하는 기법의 성능을 검증하기 위하여 모의실험을 수행하였으며, 모의실험 결과를 통하여, 제안하는 하이브리드 프리코더 및 전력 분배 상수 설계 기법이 기존의 송신단 ZF 프리코딩 기법보다 더 우수한 신호대 간섭 잡음비 (SINR) 성능을 갖는다는 것을 보인다.

Abstract

In this paper, we propose a joint design of hybrid precoder and power splitting factor in massive multiple-input single output (MISO) systems when the number of radio frequency (RF) chains is less than that of the transmit antennas. To compensate the weakness of the conventional transmit zero-forcing (ZF) precoding scheme that does not consider an additive noise, a proposed scheme uses a signal-to-leakage plus noise ratio (SLNR) as a cost function. We design the hybrid precoding vector and power splitting factor to maximize the SLNR with the constraint that the harvested power needs to be higher than the minimum power level. We performed computer simulation to verity the performance of the proposed scheme. Simulation results show that the proposed hybrid precoder and power splitting factor design scheme has better signal-to-interference plus noise ratio (SINR) performance than the conventional transmit ZF precoding scheme.

Keywords:

massive MIMO, power transfer, hybrid precoder, power splitting

Ⅰ. 서 론

이동 통신 환경에서 가장 중요한 성능 지표 중의 하나는 데이터 전송률이며, 지난 수십 년 동안 데이터 전송률을 높이려는 노력이 계속되어 왔다. 최근에 데이터 전송률을 획기적으로 높일 수 있는 방법 중의 하나로 대용량(Massive) 다중 입력 다중 출력(MIMO, Multiple Input Multiple Output) 기술에 대한 연구가 활발하게 진행되고 있다[1][2]. 용량 MIMO 기술에서 기지국은 수십 개 또는 수백 개의 안테나를 사용하여 여러 개의 단말기들에게 동시에 데이터를 전송한다.

대용량 MIMO 기술에서 다중 사용자 간섭 신호를 줄이기 위해서는 적절한 프리코딩을 적용해야 된다. 이와 같은 과정을 효율적으로 진행하기 위해서는 기지국 전송 장치에 고주파 대역 신호 처리 체인(RF chain)이 충분히 많이 있어야 된다. 기존의 통신 환경에서는 일반적으로 RF 체인의 개수는 송신 안테나의 개수와 같도록 설계한다. 그러나 대용량 MIMO 기술에서는 송신 안테나의 개수가 매우 많기 때문에, RF 체인의 개수를 송신 안테나 개수만큼 많이 설치하는 것은 너무 많은 비용을 필요로 하기 때문에, 현실적으로는 적용이 불가능하다.

이러한 문제를 해결하기 위하여, 최근에는 하이브리드 프리코딩 기술에 대한 연구가 진행되고 있다[3][4]. 하이브리드 프리코더는 RF 대역 프리코더와 기저 대역 프리코더의 직렬 연결로 구성되어 있다. RF 대역 프리코더 행렬은 사이즈가 매우 크지만, 단순한 위상 변환 회로를 통해서 쉽게 구혀할 수 있다. 그리고 그 행렬의 모든 원소들은 크기는 같고 위상만 다르도록 설계한다. 또한, 기저 대역 프리코더 행렬은 상대적으로 사이즈가 작지만, 그 행렬의 원소들은 임의의 크기 및 위상을 가질 수 있도록 설계한다.

한편, 최근에 무선 전송 신호를 통해 단말기에게 정보 데이터와 전력을 동시에 전송하는 기술에 대한 많은 연구가 진행되고 있다[5]-[7]. 송신단에서는 프리코딩 기술을 적용하여 간섭 신호를 줄여주고, 수신단에서는 수신 신호를 전력 분배 회로에 통과시킴으로써, 정보 검출용 수신 신호와 전력 수확 수신 신호를 발생시킨다.

따라서 관련 문헌들에서는 수확 가능 전력에 대한 최소 조건을 만족시키도록 하면서 신호대 간섭 잡음비(SINR, Signal-to-Interference plus Noise Ratio)를 최대화시키도록 프리코더 및 전력 분배 상수를 설계한다. 그러나 임의의 단말기에 대한 SINR은 모든 단말기들에 대한 프리코딩 벡터들의 함수이기 때문에, SINR을 최대화시키는 최적화 문제에서는 모든 프리코딩 벡터들을 동시에 설계해야 된다. 또한, SINR 함수는 프리코딩 벡터와 전력 분배 상수에 대한 볼록 함수(Convex function)가 아니기 때문에, 수학적 분석해를 구하는 것은 불가능하다. 더욱이 이러한 환경에서 SINR을 최대화시키는 하이브리드 프리코더를 설계하는 문제는 훨씬 더 어렵고 매우 복잡한 반복 기법을 통해서만 최적해를 구할 수 있다.

이처럼 정보 데이터와 전력을 동시에 전송하는 환경에 대한 기존 하이브리드 프리코딩 기법들 중에서 가장 주목할 만한 방법 중의 하나는 송신단 ZF(Zero-Forcing) 기법을 적용한 하이브리드 프리코딩 기법이다[8][9]. 이 기법에서는 임의의 단말기에 대한 프리코딩 벡터가 모든 간섭 채널 벡터에 직교하도록 설계한다.

따라서 간섭 신호가 완전히 제거되고, SINR에 대한 표현식이 매우 간단해지기 때문에, 최적화 문제에 대한 해를 쉽게 구할 수 있다. 그러나 송신단 ZF 기반의 프리코딩 기법은 수신 신호에 존재하는 부가잡음을 고려하지 않고 프리코딩 벡터 및 전력 분배 상수를 설계하기 때문에 신호대 잡음비(SNR, Signal-to-Noise Ratio)이 낮은 환경에서는 성능이 저하되는 단점이 발생한다.

본 논문은 기존 송신단 ZF 기반의 프리코더 및 전력 분배 상수 설계 기법의 문제점을 보완하기 위하여 부가잡음을 고려한 신호대 누수 잡음비(SLNR, Signal-to-Leakage plus Noise Ratio) 기반의 설계 기법을 제안한다. 누수 신호는 기지국이 임의의 목표 단말기에게 전송한 신호가 모든 다른 단말기들에게 전달되는 신호의 전력 합을 의미한다[10].

따라서 본 논문에서는 정보 데이터와 전력을 동시에 전송하는 다중 사용자 대용량 다중 입력 단일 출력(MISO, Multiple Input Single Output) 환경에서, RF 체인의 개수가 송신 안테나의 개수보다 적은 경우에 SLNR 기반의 하이브리드 프리코더 및 전력 분배 상수를 설계하는 방법을 제안한다. 구체적으로는, 수확 가능 전력에 대한 최소 조건을 만족시킨다는 제약 조건 하에서, SLNR을 최대화 시키도록 하이브리드 프리코더 및 전력 분배 상수를 설계하는 것이다. 프리코딩 벡터와 전력 분배 상수에 대한 최적화 문제는 볼록 함수가 아니므로, 반복 기법을 통하여 최적해를 구하는 방법을 제시한다. 제안 기법의 성능을 검증하기 위하여, 컴퓨터 모의실험을 수행하였으며 모의실험 결과를 통하여 제안하는 하이브리드 프리코딩 및 전력 분배 상수 설계 기법이 기존의 송신단 ZF 하이브리드 기법보다 더 우수한 SINR 성능을 갖는다는 것을 보인다.

Ⅱ. 시스템 모델

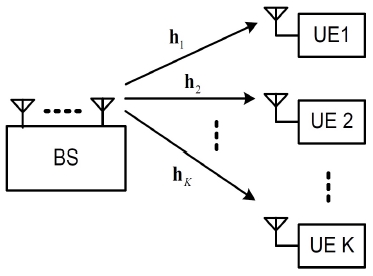
그림 1은 본 논문에서 고려하는 다중 사용자 대용량 MISO 시스템에 대한 모델을 보여준다. 이 그림에서 BS는 기지국을 의미하며, UE는 사용자 단말기를 의미한다. 기지국은 동일한 시간 및 주파수 자원을 사용하여 K개의 단말기들에게 서로 다른 데이터를 전송한다. 이때, 기지국은 N개의 송신 안테나를 가지고 있고, 단말기들은 한 개의 수신 안테나를 갖는다고 가정한다. 그리고 h_k는 기지국으로부터 단말기 k까지의 채널 벡터를 나타낸다.

Fig. 1.

Multiuser massive MISO system model

기지국이 단말기 k에게 전송하는 데이터를 s_k라고 하자. 이 때, s_k는 평균이 0이고 분산이 1인 확률 변수를 의미한다.

그리고 s_k를 전송하기 위하여 사이즈가 N×1인 프리코딩 벡터 w_k를 적용한다고 가정하자. 전체 데이터 벡터를 s=[s₁,...,s_K]^T라고 정의하고, 전체 프리코딩 행렬을 W=[w₁,...,w_K]라고 정의하면, 기지국에서의 송신 신호는 d= Ws라고 표현할 수 있다.

한편, RF 체인의 개수 M이 송신 안테나의 개수 N보다 작다고 하면, 기저 대역 프리코딩과 RF 대역 프리코딩으로 구성된 하이브리드 프리코딩을 적용한다. 따라서, 하이브리드 프리코딩 행렬은 다음과 같이 다시 쓸 수 있다.

W = F R G B = F R g B, 1, …, g B, K

(1)

여기에서 G_B는 기저 대역에서 적용하는 프리코딩 행렬을 의미하며, M×K사이즈는 이다. 또한, F_R은 RF 대역에서 적용하는 프리코딩 행렬을 의미하며, 사이즈는 N×M이다. 따라서, w_k를 다음과 같이 표현할 수 있다.

w k = F R g B, k

(2)

대용량 MISO 시스템에서는 N이 M보다 훨씬 크기 때문에 계산량을 줄이기 위하여 RF 대역 프리코딩 과정은 위상 변환기와 같은 간단한 방식으로 처리하도록 설계한다. 이로 인해, F_R의 각 원소들은 진폭이 1이고 위상만 서로 다른 복소수 값을 갖는다. 한편, G_B는 F_R보다 사이즈가 훨씬 작은 행렬로서, 다중 사용자 간섭을 줄이기 위하여 사용되며, 각 원소는 임의의 진폭과 위상을 가질 수 있다.

단말기 k에서의 수신 신호는 다음과 같이 쓸 수 있다.

x k = h k H Ws + z k = h k H ∑ j = 1 K w j s j + z k

(3)

여기에서 h_k는 기지국으로부터 단말기 k까지의 채널 벡터를 의미하며, 사이즈는 N×1이다. 그리고 z_k는 평균이 0이고 분산이 $σ z 2$ 인 백색 가우시안 부가잡음(AWGN)을 의미한다.

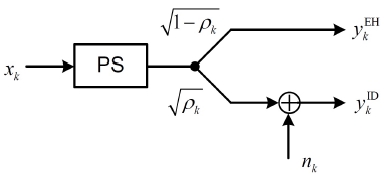
그림 2는 단말기 k에서의 전력 분배 과정을 나타내며, ρ_k는 전력 분배 상수를 나타낸다. 수신 신호 x_k에 있는 전력 중에서 ρ_k에 해당되는 전력은 정보 데이터 검출을 위해서 사용되고, 나머지 (1 - ρ_k)에 해당되는 전력은 전력 수확을 위해서 사용된다.

Fig. 2.

Power splitting process at UE k

정보 검출을 위해 사용되는 수신 신호 $y k ID$ 는 다음과 같이 쓸 수 있다.

y k ID = ρ k x k + n k = ρ k ∑ j = 1 K h k H w j s j + z k + n k

(4)

여기에서 n_k는 RF 대역 신호를 기저 대역 신호로 변환하면서 발생하는 회로 AWGN을 나타내며 평균은 0이고 분산은 $σ n 2$ 인 특성을 갖는다.

이 때, 수신 SINR은 다음과 같이 쓸 수 있다.

S I N R k = h k H w k 2 ∑ j = 1 j ≠ k K h k w j 2 + σ z 2 + σ n 2 / ρ k

(5)

한편, 전력 수확을 위해 사용되는 전력 수신 신호는 다음과 같이 쓸 수 있다.

y k EH = 1 - ρ k x k = 1 - ρ k ∑ j = 1 K h k H w j s j + z k

(6)

전력 수신 신호를 이용하여 수확 가능한 전력은 다음과 같이 쓸 수 있다.

Q k = ζ k E y k EH 2 ≈ ζ k 1 - ρ k ∑ j = 1 K h k H w j 2

(7)

여기에서 ζ_k는 전력 수확 장치에서의 변환 효율을 나타내며, 0 < ζ_k < 1인 값을 갖는다. 식 (6)에서 AWGN 성분인 z_k에 의해 수확 가능한 전력은 $ζ k 1 - ρ k σ n 2 N$ 에 의해 표현되며, 이 값은 다른 수확 전력 값에 비해서 매우 작다. 따라서 식 (7)에서 z_k에 의한 성분은 생략하였다.

하이브리드 프리코딩 벡터 w_k를 설계하는 방법 중의 하나는 전력 수확 조건을 만족시키면서 SINR을 최대화시키는 것이다. 이러한 최적화 문제를 수학식으로 표현하면 다음과 같이 쓸 수 있다.

max w 1, …, w K, ρ k, ⁡ h k H w k 2 ∑ j = 1 j ≠ k K h k w j 2 + σ z 2 + σ n 2 / ρ k

(8)

subject to $ζ k 1 - ρ k ∑ j = 1 K h k H w j 2 ≥ e k$
w_k = F_Rg_B,k

여기에서 e_k는 수확 전력 임계치를 의미한다. 이식을 살펴보면, SINR과 수확 전력에 대한 식은 모든 단말기들에 대한 프리코딩 벡터들의 함수이기 때문에, 모든 프리코딩 벡터들을 동시에 설계해야 된다. 또한, SINR 함수는 프리코딩 벡터에 대한 볼록 함수가 아니기 때문에, 이 문제에 대한 해를 구하는 것은 매우 어렵다.

프리코딩 벡터들 간의 연관성을 제거하고 문제를 단순화시킬 수 있는 가장 쉬운 방법 중의 하나는 송신단에서 ZF 기술을 적용하는 것이다[9]. 그러나 송신단 ZF 기술은 부가잡음을 고려하지 않고 프리코딩 벡터를 설계하는 방식이기 때문에, SNR이 낮은 환경에서는 성능이 저하되는 단점이 발생한다.

Ⅲ. 제안하는 하이브리드 프리코더 설계 방법

이 장에서는 본 논문에서 제안하는 하이브리드 프리코더 및 전력 분배 상수 설계 기법에 대해서 설명한다. 기존의 송신단 ZF 기법의 문제점을 보완하기 위하여, 본 논문에서는 SLNR 기반의 설계 기법을 제안한다.

정보 수신 신호에 대한 식 (4)로부터 단말기 k에 대한 SLNR 표현식은 다음과 같이 구할 수 있다 [10].

S L N R k = h k H w k 2 ∑ j = 1, j ≠ k K h j H w k 2 + σ z 2 + σ n 2 / ρ k

(9)

식 (5)와 식 (9)를 비교하면, SINR_k는 모든 단말기들의 프리코딩 벡터들의 함수이지만, SLNR_k는 단말기 k에 대한 프리코딩 벡터 w_k만의 함수라는 것을 알 수 있다.

따라서 SINR_k 대신에 SLNR_k을 사용하는 최적화 문제는 다음과 같이 쓸 수 있다.

max w K, ρ k ⁡ h k H w k 2 ∑ j = 1, j ≠ k K h j H w k 2 + σ z 2 + σ n 2 / ρ k

(10)

subject to $ζ k 1 - ρ k h k H w k 2 ≥ e k$
w_k = F_Rg_B,k

이 식에서 주어진 수확 가능 전력에 대한 제약 조건을 만족시키면, 식 (8)에서 주어진 제약 조건도 만족시킨다.

식 (10)을 만족하는 하이브리드 프리코딩 벡터를 구하기 전에, 먼저 최대 RF 체인을 갖는 경우에 대한 해를 구한다. 즉, RF 체인의 개수가 송신 안테나의 개수와 같고, w_k = F_Rg_B,k라는 제약 조건을 사용하지 않는 경우에 대해서 최적해를 구한다.

식 (10)은 w_k와 ρ_k에 대한 볼록 함수가 아니기 때문에, 수학적 분석해를 구하는 것은 불가능하다. 따라서 반복 기법을 통해서 해를 구한다. 먼저, ρ_k가 주어진 경우에 최적화 문제에 대한 해는 다음과 같이 구할 수 있다 [10].

w k opt = m a x_geig h k h k H, ∑ j = 1, j ≠ k K h j h j H + σ z 2 I N + σ n 2 / ρ k I N

(11)

마찬가지로, $w k opt$ 가 주어진 경우에, ρ_k에 대한 최적해는 다음과 같이 구할 수 있다.

ρ k opt = 1 - e k ζ k ⋅ h k H w k opt 2

(12)

식 (11)과 (12)를 반복적으로 적용함으로써 최적해를 구할 수 있다. 최대 RF 체인을 갖는 최적화 문제에 대한 해를 다음과 같이 정의하자.

W opt = w 1 opt,…, w K opt

(13)

이제 RF 체인의 개수가 송신 안테나의 개수보다 적은 경우에 대해서, 하이브리드 프리코딩 행렬을 설계하는 방법을 살펴보자. W_opt와 $ρ k opt$ 에 대한 정보를 가지고 있기 때문에, 하이브리드 프리코더 W= F_RG_B는 W_opt에 가깝도록 설계한다. 이것을 수식으로 표현하면 다음과 같다.

m i n F R, G B W opt - F R, G B 2 F

(14)

subject to F_R ∈ Q

여기에서 ∥ㆍ∥_F은 Frobenius 놈을 의미하고, Q는 사이즈가 N×M 이고, 모든 원소의 크기가 1인 행렬들의 집합을 나타낸다. 제약 조건 F_R ∈ Q 때문에, 식 (14)는 F_R에 대한 볼록 함수가 아니다. 따라서 식 (14)에 대한 분석해를 구하는 것은 불가능하며, 반복 기법을 통해서 해를 구할 수 있다.

n번째 반복 기법을 통해 $G B n$ 이 주어졌다고 하면, 먼저 F_R ∈ Q이라는 제약 조건을 사용하지 않고, 다음 최적화 문제에 대한 해를 구한다.

F ¯ R n + 1 = arg ⁡ m i n F R W opt - F R, G B n 2 F

(15)

이 문제에 대한 해 $F ¯ R n + 1$ 는 다음과 같이 주어진다.

F ¯ R n + 1 = W opt G B n H G B n - 1 G B n H

(16)

이제 F_R은 F_R ∈ Q이라는 조건을 만족시켜야 되기 때문에, $F ¯ R n + 1$ 로부터 $F R n + 1$ 을 구하는 방법은 다음과 같다. $F ¯ R n + 1$ 의 (p, q)번째 원소의 각을 $∠ F ¯ R n + 1 p, q = ϕ p, q$ 라고 표현하면, F_R ∈ Q을 만족시키기 위하여 $F R n + 1$ 의 (p, q)번째 원소를 다음과 같이 설정한다.

F R n + 1 p, q = e j ϕ p, q

(17)

이제 $F R n + 1$ 이 주어지면, $G B n + 1$ 은 다음 최적화 문제를 통해 구한다.

max g B, K, ρ k ⁡ h k H F R n + 1 g B, k 2 ∑ j = 1, j ≠ k K h j H F R n + 1 g B, k 2 + σ z 2 + σ n 2 / ρ k

(18)

subject to $ζ k 1 - ρ k h k H F R n + 1 g B, k 2 > e k$

이 식에 대한 해는 다음과 같이 구할 수 있다.

ρ k n + 1 = 1 - e k ζ k ⋅ h k H F R n + 1 g B, k n + 1 2

(19)

g B,k n+1 = max ≥ig F R n+1 H h k h k H F R n+1, ∑ j = 1, j ≠ k K F R n+1 H h j h j H F R n+1 + σ z 2 I K + σ n 2 / ρ k n+1 I K

(20)

여기에서 $ρ k n+1$ 와 $g B, k n +1$ 는 서로 연관되어 있으므로, 반복 기법을 통해서 구할 수 있다. 그리고 임의로 주어진 임계값 Γ_th에 대해서, $W opt - F R n G R n F 2 < Γ t h$ 을 만족시킬 때까지 위에서 설명한 과정들을 반복함으로써, 최적화 문제 (14)에 대한 해를 구할 수 있다.

Ⅳ. 모의 실험

본 장에서는 제안하는 하이브리드 프리코더 및 전력 분배 상수 설계 기법의 성능을 검증하기 위하여 모의실험 결과들을 제시한다. 기지국의 송신 안테나 개수는 N=64를 사용하였고, 단말기 개수는 K=8, 32를 사용하였다. RF 체인의 개수는 M=K라고 가정하였다. 전력 변환 효율은 모든 단말기가 동일한 값을 갖는다고 가정하였고, ζ_k = 0.5을 사용하였다. 그리고 채널 부가잡음의 분산과 회로 부가잡음의 분산에 대해서 $σ n 2 = 10 × σ z 2$ 라고 가정하였다. 기지국과 단말기 간의 채널은 레일레이 평탄 페이딩(Rayleigh flat fading) 모델을 사용하여 채널을 발생하였으며, 100개의 독립적인 채널에 대해서 모의실험을 수행하였다. 그리고 각 채널에 대한 성능을 평균함으로써 제안하는 하이브리드 프리코딩 기법과 기존의 하이브리드 송신단 ZF 프리코딩 기법의 성능을 구하였다. 수신 SNR은 다음과 같이 정의하였다.

S N R = E s k 2 E z k 2 = 1 σ z 2

(21)

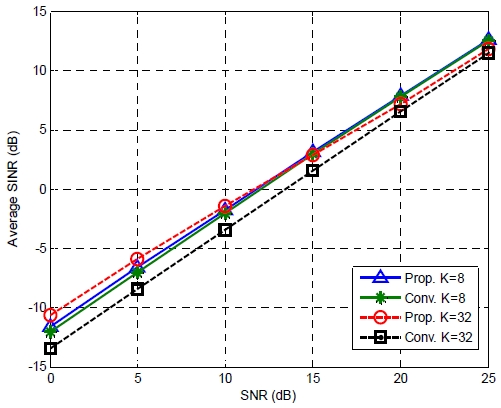
그림 3은 제안하는 하이브리드 프리코더와 기존의 송신단 ZF 프리코더에 대한 평균 수신 SINR 성능을 비교한다. 이 그림에서 ‘Prop.’는 제안하는 하이브리드 프리코더의 성능을 나타내고, ‘Conv.’는 기존의 송신단 ZF 하이브리드 프리코더의 성능을 나타낸다. 기지국 송신 안테나의 개수는 N = 64이고, 단말기의 개수는 K = 8, 32이다. 수확 전력 임계값은 모든 단말기에 대해서 동일한 값을 사용하였으며, e_k = 0.001을 사용하였다.

Fig. 3.

Average SINR performance comparison when N = 64, K = 8, 32, ek = 0.001

이 결과로부터 단말기 수가 적을 때 (K=8)는 제안하는 프리코더와 기존의 프리코더의 성능이 비슷하다는 것을 알 수 있다. 그러나 단말기 수가 많은 경우(K=32), SNR이 낮은 영역에서는 제안하는 하이브리드 프리코더가 기존의 하이브리드 프리코더보다 더 우수한 성능을 갖는다는 것을 알 수 있다. 이것은 기존의 프리코더는 부가잡음을 고려하지 않고 프리코더를 설계하기 때문에 SNR이 낮을 때는 성능 저하가 발생하는 것이다.

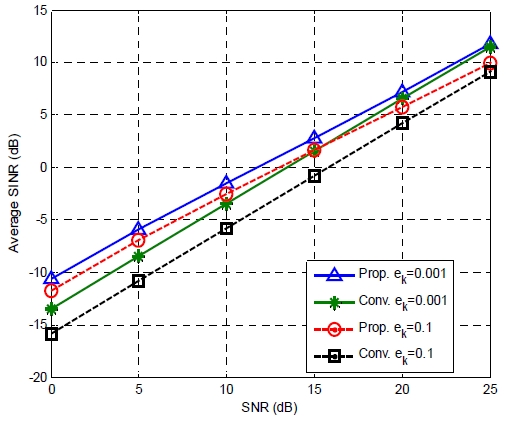
그림 4는 여러 가지 수확 전력 임계값에 대해서 제안하는 프리코더와 기존의 프리코더 간의 평균 수신 SINR 성능을 비교한다. 기지국 송신 안테나의 개수는 N = 64이고, 단말기의 개수는 K = 32이다. 수확 전력에 대한 임계값은 e_k = 0.1과 e_k = 0.001을 사용하였다. 이 결과로부터 수확 전력에 대한 두 가지 임계값에 대해서, 제안하는 하이브리드 프리코더가 기존의 송신단 ZF 기반의 프리코더보다 더 우수한 성능을 갖는다는 것을 알 수 있다. 또한, 수확 전력 임계값이 증가하면, 제안하는 기법과 기존 기법의 평균 SINR 성능이 감소한다는 것을 알 수 있다. 이것은, 수확 전력을 증가시키기 위해서는 전력 분배 회로에서 수신 신호의 더 많은 부분들을 전력 회로로 전달하기 때문에, 정보 검출을 위해서 사용할 수 있는 신호의 세기가 작아지기 때문이다.

Fig. 4.

Average SINR comparison for several harvest power value when N = 64, K = 32, ek = 0.1, 0.001

표 1은 SNR=15dB일 때 기존 기법과 제안 기법의 평균 SINR 성능을 비교한다. 이 표로부터 제안하는 기법 (Proposed)이 기존 기법 (Previous)보다 모든 경우에 대해 성능이 우수하다는 것을 알 수 있으며 단말기 수 K가 클수록, 그리고 수확 전력 임계값 e_k이 클수록 성능 차이가 많이 난다는 것을 알 수 있다.

Table 1.

Average SINR comparison: SNR=15dB

Ⅴ. 결 론

본 논문에서는 정보 데이터와 전력을 동시에 전송하는 다중 사용자 대용량 MISO 채널 환경에서 RF 체인의 개수가 송신 안테나의 개수보다 적은 경우에 대한 하이브리드 프리코더 및 전력 분배 상수를 설계하는 방법을 제안하였다. 기존의 송신단 ZF 프리코딩 기법의 문제점을 보완하기 위하여, SLNR 기반의 프리코딩 설계 기법을 제안하였다. 수확 가능 전력에 대한 제약 조건을 만족시키도록 하면서, SLNR을 최대화시키도록 프리코딩 벡터 및 전력 분배 상수를 설계하였다. 관련된 최적화 문제는 프리코딩 벡터에 대한 볼록 함수가 아니기 때문에, 수학적 분석해를 구하는 것은 불가능하며, 반복 기법을 통해서 해를 구하는 방법을 제시하였다. 컴퓨터 모의 실험을 통하여 제안하는 하이브리드 프리코더가 기존의 송신단 ZF 프리코더보다 더 우수한 SINR 성능을 갖는다는 것을 보였다.

Acknowledgments

이 논문은 공주대학교 연구년 사업에 의하여 연구되었음.

References

E. G. Larsson, O. Edfors, F. Tufvesson, and T. L. Marzetta, "Massive MIMO for next generation wireless systems", IEEE Communications Magazine, Vol. 52, No. 2, pp. 186-195, Feb. 2014. [https://doi.org/10.1109/MCOM.2014.6736761]
J. H. Kim, C. Mun, and C. H. Jung, "Analysis on the characteristics of Rician fading in massive MIMO systems", Journal of KIIT, Vol. 13, No. 5, pp. 43-48, May 2015. [https://doi.org/10.14801/jkiit.2015.13.5.43]
Z. Wang, M. Li, Q. Liu, and A. Lee Swindlehurst, "Hybrid precoder and combiner design with low-resolution phase shifters in mmWave MIMO systems", IEEE Journal of Selected Topics in Signal Processing, Vol. 12, No. 2, pp. 256-269, May 2018. [https://doi.org/10.1109/JSTSP.2018.2819129]
R. Zhang, W. Zou, Y. Wang, and M. Cui, "Hybrid precoder and combiner design for single-user mmWave MIMO systems", IEEE Access, Vol. 7, pp. 63818-63828, Jan. 2019. [https://doi.org/10.1109/ACCESS.2019.2895314]
R. Zhang and C. K. Ho, "MIMO broadcasting for simultaneous wireless information and power transfer", IEEE Transactions on Wireless Communications, Vol. 12, No. 5, pp. 1989-2001, May 2013. [https://doi.org/10.1109/TWC.2013.031813.120224]
X. Zhou, R. Zhang, and C. K. Ho, "Wireless information and power transfer: Architecture design and rate-energy tradeoff", IEEE Transactions on Communications, Vol. 61, No. 11, pp. 4754-4767, Nov. 2013. [https://doi.org/10.1109/TCOMM.2013.13.120855]
Q. Shi, L. Liu, W. Xu, and R. Zhang, "Joint transmit beamforming and receive power splitting for MISO SWIPT systems", IEEE Transactions on Wireless Communications, Vol. 13, No. 6, pp. 3269-3280, Jun. 2014. [https://doi.org/10.1109/TWC.2014.041714.131688]
Z. Zong, H. Feng, F. R. Yu, N. Zhao, T. Yang, and B. Hu, "Optimal transceiver design for SWIPT in K-user MIMO interference channels", IEEE Transactions on Wireless Communications, Vol. 15, No. 1, pp. 430-445, Jan. 2016. [https://doi.org/10.1109/TWC.2015.2474857]
Y. F. Wang and J. H. Lee, "A ZF-based precoding scheme with phase with noise suppression for massive MIMO downlink systems", IEEE Transactions on Vehicular Technology, Vol. 67, No. 2, pp. 1158-1173, Feb. 2018. [https://doi.org/10.1109/TVT.2017.2749598]
M. Sadek, A. Tarighat, and A. H. Sayed, "A leakage-based precoding scheme for downlink multi-user MIMO channels", IEEE Trans. Wireless Communication, Vol. 6, No. 5, pp. 1711-1721, May 2007. [https://doi.org/10.1109/TWC.2007.360373]

저자소개

서 방 원 (Bangwon Seo)

1997년 2월 : KAIST 전기 및 전자공학과(공학사)

1999년 2월 : KAIST 전기 및 전자공학과(공학석사)

2010년 2월 : KAIST 전기 및 전자공학과(공학박사)

2004년 11월 ~ 2013년 2월 : 한국전자통신연구원 선임연구원

2013년 3월 ~ 현재 : 공주대학교 부교수

관심분야 : 이동통신, 단말간 직접통신 (D2D), 다중 안테나 기술 (MIMO), 프리코더 설계, 인공지능

	K=8	K=32
	e_k=0.001	e_k=0.01	e_k=0.001
Previous	2.90	-0.83	1.54
Proposed	3.07	1.64	2.81