CMOS 이미지 센서의 임펄스 잡음 제거를 위한 푸아송 잡음 모델 기반 적응적 중간값 필터
초록
이미지 센서는 제조상의 결함으로 인해서 일부 화소가 영구적인 손상을 가진다. 이런 화소들은 임펄스 잡음으로 모델링되므로 중간값 필터를 사용하여 효과적인 제거가 가능하다. 그러나 중간값 필터는 영상의 선예도를 떨어뜨리므로, 잡음 성분에 대해서만 적응적으로 적용하는 방법들이 널리 사용되어 왔다. 본 논문에서는 이미지 센서의 임펄스 잡음 제거를 위해서 개선된 적응적 중간값 필터 알고리즘을 제안한다. 첫 단계에서는 이미지 센서로 취득된 영상 값의 변화는 푸아송 분포로 모델링되므로 이를 이용하여, 잡음을 분류한다. 잡음 화소에 대해서는 3x3 영역에서 수평수직 방향의 5개의 데이터에 대한 중간값, 대각선 방향의 5개 데이터에 대한 중간값과 원 데이터로부터 구한 중간값을 적용한다. 실험결과 제안한 방법은 중간값 필터와 비교할 때, 83% 이하의 계산량에서 평균 7 dB의 성능 향상을 보여준다.
Abstract
Image sensors have a few pixels that are permanently damaged due to manufacturing defects. These pixels are regarded as impulse noise and can be removed effectively using a median filter. Since the median filter reduces the sharpness of the image, however, adaptive methods have been widely used. In this paper, we propose an improved and effective median filter algorithm for removing impulse noise. In the first step, the noise and the normal signal are classified by considering that the natural noise model of the image is represented by the Poisson distribution. Then the median value is applied based on the median value of the kernel consisting of five elements in the horizontal and vertical directions, the median value of the kernel consisting only of five elements in the diagonal directions, and the original image data. The proposed method shows a 7 dB average improvement in objective quality under 83% of the calculations compared to the normal median filter.
Keywords:
ISP, sensor defect, poisson model, shot noise, impulse noise, median filterⅠ. 서 론
ISP(Image Signal Processor)는 이미지 센서에서 출력되는 영상 데이터가 가지는 CFA(Color Filter Array) 패턴[1]을 영상 압축에서 사용되는 YCbCr 영상 데이터로 변환하는 것을 포함하는 일련의 알고리즘들을 수행한다. 일반적으로 동영상은 하드웨어 ISP를 사용하고, 정지영상은 하드웨어 ISP와 소프트웨어 ISP를 혼용하거나, 소프트웨어 ISP만으로 처리한다. 최근 출시된 플래그쉽 스마트폰에 장착된 AP(Application Processor)에는 NPU(Neural Processing Unit)가 기본적으로 탑재되기 때문에 이를 이용하여 딥러닝 기반의 영상처리 알고리즘을 적용하는 추세도 확산되는 중이다. ISP[2][3]에서 가장 필요한 기능은 최적의 색재현과 선예도 향상이며, 특히 선예도 향상을 위해서는 CFA 영상 보간(Interpolation)과 잡음제거의 중요성이 강조된다.
이미지 센서는 각 화소에서 RGB 삼원색을 동시에 표본화하는 대신, RGB 성분 중에서 하나의 색성분만을 표본화함으로써 비용효율적으로 구현되어 있다. 표본화된 색성분 패턴을 CFA라고 한다. 보간은 이로부터 RGB 영상을 생성하는 과정이다[4]. 따라서 이 과정을 통해서 입력된 데이터의 잡음은 주변으로 확산될 수 있으므로, 원활한 보간을 위해서는 입력 영상에 내재된 잡음을 미리 제거해야 한다.
CFA 영상은 2×2 배열에 1개의 Red, 1개의 Blue, 2개의 Green 성분으로 구성된다. 이 때 2개의 Green 성분은 주변 색성분으로 받는 영향이 상이하므로, 동등한 신호 특성을 가지는 것으로 간주되지는 않는다. Red와 수평방향으로 인접한 Green은 Gr라고, Blue와 수평방향으로 인접한 Green은 Gb로 명명하여, 서로 다른 신호인 것처럼 다룰 수 있다. 따라서 2×2 CFA는 서로 상이한 색성분 4개로 구성된 것으로 볼 수 있으므로, 이들을 같은 색성분 별로 모은 후에 독립적으로 처리할 수 있다.
그림 1은 4×4 해상도의 영상을 4개의 2×2 해상도 영상을 추출하는 과정을 보여준다. 그러므로 이미지 센서의 임펄스 잡음을 제거한다는 것은 각 성분에 대해서 임펄스 잡음을 독립적으로 제거한다는 것과 동일하다. 이미지 센서로부터의 출력 영상에서의 임펄스 잡음은 보간에 악영향을 줄 수 있으므로, 선별적으로 제거할 필요가 있다[5].
Example of partitioning CFA pattern image into 4 images
Sony에서 양산 중인 이미지 센서의 사양서를 따르면, 센서 중심부 640×480 영역에서 임펄스 잡음의 수가 24개 이하인 것은 정상인 것으로 규정하고 있다[6]. 이와 같은 불연속적인 임펄스 잡음은 중간값(Median) 필터에 의해서 완벽하게 제거된다. 그러나 임펄스 잡음이 아닌 화소들에 대해서 선예도가 열화되는 것은 피할 수 없다. 따라서 임펄스 잡음으로 분류하는 것과, 중간값 필터를 적용하기 위한 커널의 형태를 결정하는 방법에 따라 결과 영상의 품질이 달라지게 된다.
센서에서 만들어지는 영상 데이터는 푸아송 분포를 따르기 때문에, 푸아송 모델을 활용하여 잡음을 분리한 후 3×3 영역에서 수평수직 방향으로 구성된 5개의 데이터에 대해서 중간값 필터를 적용하는 방법[7]이 최근에 제안되어, 단순한 중간값 필터를 적용한 경우에 비해서 6dB 이상의 성능 향상을 보여줬다. 본 논문은 이 방법에 따른 영상 화질을 더욱 향상시키기 위하여 개선된 중간값 필터를 제안한다. 본 논문의 구성은 다음과 같다. 2장과 3장에서의 기존에 제안된 중간값 필터와 제안한 중간값 필터의 구조를 각각 서술한다. 4장에서는 제안한 알고리즘을 적용한 결과 화질을 정량적으로 분석하고, 마지막 장에서는 결론을 내린다.
Ⅱ. 푸아송 모델 기반 적응적 중간값 필터[7]
2.1 수평수직 커널
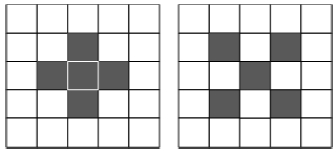
그림 2는 Sony 이미지 센서에서 불량품으로 판정되는 임펄스 잡음의 패턴을 도시한 것이다[6]. 그림에서 ●는 결함을 나타내는데, 백색결함(White defect) 혹은 흑색결함(Black defect)을 구분되며, 상이한 종류의 결함이 바로 인접하는 것은 정상으로 간주한다. 1번 항목과 2번 항목은 수평방향과 수직방향으로 2칸 간격으로 인접한 동종의 결함이 발생할 경우에는 불량품으로 간주한다는 뜻이다.
Impulse noise pattern unallowed in Sony image sensors
센서와 ISP가 독립적으로 구성되어 있을 때, 센서 데이터를 ISP 내에서 그림 1과 같이 표본화하면, 표본화된 영상에서는 동종의 결함이 연속적으로 발생하지 않는 것을 보장한다. 결함에 의해서 발생하는 잡음은 연속적으로 발생하지 않기 때문에 임펄스 잡음으로 모델링할 수 있다.
그림 3은 임펄스 잡음을 제거하기 위해서 필요한 가장 작은 형태의 커널을 나타낸다. 중심에 임펄스 잡음으로 분류된 화소가 있다면, 인접한 4개의 화소에는 임펄스 잡음이 존재하지 않는다. 따라서 커널을 구성하는 5개의 데이터에 대해서 중간값을 구함으로써 임펄스 잡음을 제거하는 것이 가능하다.
Configuring the cross kernel to remove impulse noise
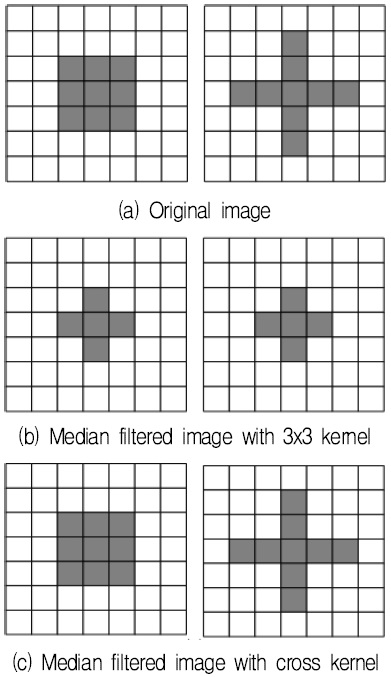
그림 4(a)는 수평수직 윤곽선을 가지는 패턴을 보여주고 있는데, 여기에 3×3 중간값 필터를 적용하면 그림 4(b)와 같이 모서리가 침식된 결과를 보여준다. 그러나 그림 3의 십자커널을 대해서 중간값 필터를 적용하면 그림 4(c)와 같이 모서리에서의 원형이 유지된다.
Image artifact by median filtering
2.2 산탄잡음 모델에 의한 잡음 판단
빛의 세기는 주어진 시간에 동안 입사된 광량 또는 광자(Photon)의 양에 의해서 결정된다. 입사된 광자의 수는 이산적인 흐름을 가지고 있으므로, 같은 표면에 같은 시간 동안 노출되더라도 입사된 광자의 양은 변동성을 가지게 된다. 산탄잡음(Shot Noise)은 이러한 변동성을 나타내며, 영상에서 발생하는 잡음 중에서 가장 높은 비중을 차지한다[5]. 입사되는 광자가 λ개가 되도록 노출시간이나 광량을 조정한 경우, 광자의 수를 나타내는 확률변수 X는 푸아송(Poisson) 분포를 따르므로 분산 σ2 = λ, 평균 μ = λ을 가진다. X에 정비례하는 신호를 Y라 하고, Y = cX일 때, Y의 평균 μY과 분산 σ2Y는 식 (1)과 같다. 또한 이로부터 Y의 표준편차 σY과 평균 μY과의 관계를 도출할 수 있다.
| (1) |
X가 광자의 수라고 할 때, Y는 광전변환에 의한 이미지 센서 출력값을 나타낸다. X가 푸아송 분포를 따르고, Y는 X에 정비례하는 신호이기 때문에 Y의 표준 편차는 Y의 평균값에 비례하게 된다. 즉, 이미지 센서의 출력값이 Y일 때, 산탄잡음은 크기는 신호의 제곱근에 비례한다. 따라서 화소 위치 (i,j)에서의 밝기값이 P(i,j)일 때, (i,j)에서 허용되는 오차의 범위에 대한 기준치 η(i,j)는 식 (2)와 같이 결정할 수 있다. 식 (2)에서 k는 사용자가 임의로 결정할 수 있는 상수로써 k=1을 기준으로 삼는다.
| (2) |
2.3 십자 커널 기반 적응적 잡음제거 알고리즘
그림 5에 임펄스 잡음 제거 알고리즘을 나타냈다.
Impulse noise reduction algorithm
변수 i,j는 영상에서의 화소위치를 나타내는 독립변수이다. P[i][j]는 화소 위치 (i,j)에서의 영상의 밝기값을 나타내는 종속변수이다.
P[i][j]가 주어지면, 잡음에 대한 판단 기준인 T를 식 (2)에 의해서 계산한다. 그리고 현재 화소를 중심으로 3×3 영역의 모든 화소들과 P[i][j]를 비교하여, 그 차이의 크기가 T를 초과하는 화소의 수를 계수하여 변수 C에 넣는다. C=1이라는 뜻은, 허용되는 오차 범위 내에서 비슷한 밝기를 가지는 화소가 주위에 없다는 뜻이므로, P[i][j]는 잡음으로 간주한다. 이 경우에는 십자커널을 구성하는 5개 화소에 대해서 중간값을 계산하여 출력하고, 그렇지 않은 경우에는 원 데이터를 출력한다.
Ⅲ. 제안한 중간값 필터
3.1 잡음 제거 커널
그림 3의 십자 커널은 수평/수직 방향의 윤곽선을 보존하는 능력이 탁월하다. 그러나 윤곽선의 대각선으로 기울어져 있을 경우에는 그림 7(c)와 같이 모서리 부분이 제거되는 부작용을 낳게 된다. 이런 문제를 해결하기 위해서 그림 6과 같이 수평수직 방향의 십자 커널과 함께 대각선 방향으로 구성된 대각 커널을 함께 사용한다.
Configuring the kernel to remove impulse noise
Image artifact by median filtering
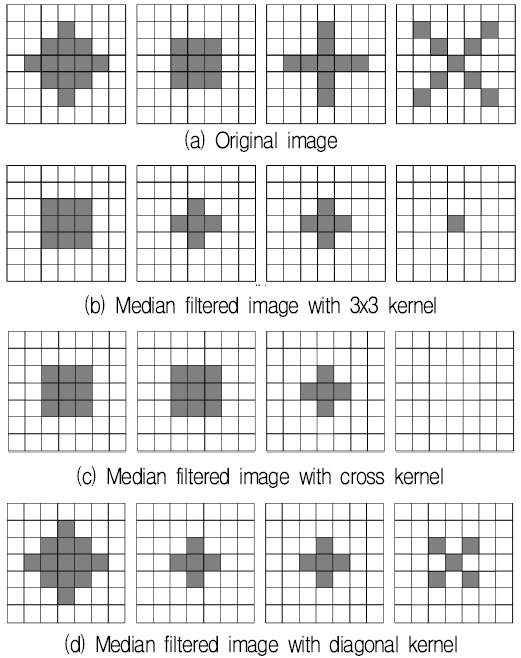
그림 7은 십자 커널과 대각 커널을 사용하여 중간값 필터를 적용할 경우의 결과를 도시한다. 그림 7(a)는 작은 객체가 가질 수 있는 일반적인 형태를 포함한다. 3×3 영역에서 사용할 수 있는 3종류의 커널에 대한 중간값 결과는 그림 7(b), 7(c), 7(d)에 각각 나타나 있다. 3×3 정사각 커널은 모든 경우에 대해서 열화된 결과를 보여주지만, 십자 커널이나 대각 커널의 경우 원형을 유지하는 경우를 선택적으로 보여주고 있다.
3.2 임펄스 잡음제거 알고리즘
임펄스 잡음 제거 알고리즘은 그림 8과 같다. P[i][j]가 주어지면, 잡음의 판단 기준인 T를 식 (2)에 의해서 계산한다. 그리고 현재 화소 준변의 3×3 영역 내의 모든 화소들의 밝기값과 P[i][j]를 비교하여, 그 차이의 절대값이 T를 초과하는 화소의 수가 1이면 잡음으로 간주한다.
Proposed impulse noise reduction algorithm
잡음인 경우 그림 6에 나타난 십자커널 내의 5개 화소의 중간값을 계산하고, 대각 커널을 구성하는 5개 화소의 중간값을 각각 계산한다. 이렇게 계산한 2개의 중간값과 원영상 데이터에 대해서 최종적으로 중간값을 구하여 출력으로 한다. 이와 같은 알고리즘을 적용할 경우 그림 7(a)의 모든 경우에 대해서 필터링을 수행하더라도 원영상이 보존된다.
Ⅳ. 모의 실험과 결과 분석
제안한 알고리즘은 49종의 512×512 해상도의 표준 테스트 영상을 사용하여 평가한다[8]. Sony의 제품 사양서에 의하면 80ppm은 정상 수준으로 간주된다. 그러나 특정한 영역에 잡음이 집중되는 경우에는 잡음 비율이 해당 영역에서 매우 높아질 수 있다. 이보다 열악한 상황을 반영하기 위해서 2000ppm의 임펄스 잡음을 표준 테스트 영상에 삽입하여 성능을 평가했다.
표 1은 3×3 커널의 중간값 필터, 적응적으로 십자 커널을 적용한 중간값 필터[7], 그리고 제안한 적응적 중간값 필터에 의한 결과를 나타낸 것이다. 제안한 방법은 3×3 정방형 커널을 가진 중간값 필터에 비해서 6.92dB, 기존의 십자 커널 기반 중간값 필터에 비해서 0.35dB 향상된 수치를 보여준다.
Average PSNR of noise reduction methods for stndard test images
주관적인 화질을 평가하기 그림 9와 10에 처리된 영상을 나타냈다. 정방형 커널에 기반을 둔 중간값 필터들은 객체의 첨예한 부분을 왜곡시키는 경향이 보이지만, 제안한 방법에서는 선예도가 유지되는 것을 알 수 있다.
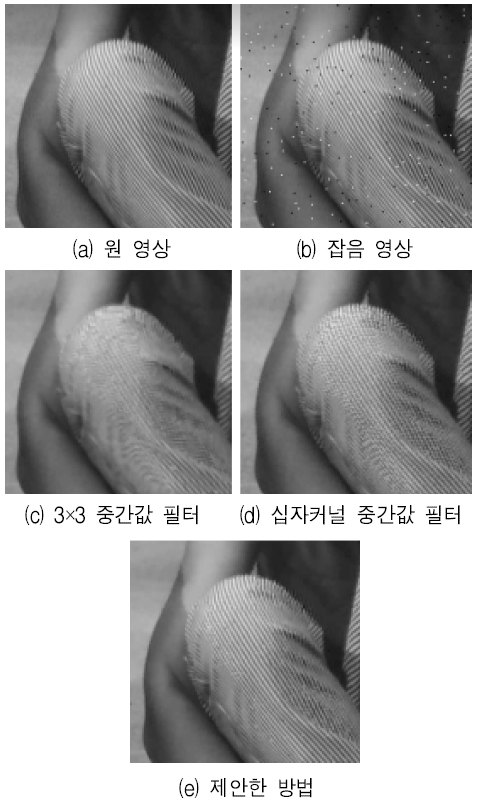
Experimental results on Barbara image, (a) Original image, (b) Noisy image, (c) 3×3 median, (d) Adaptive cross median, (e) Proposed method
Experimental results on Goldhill image, (a) Original image, (b) Noisy image (c) 3×3 median, (d) Adaptive cross median, (e) Proposed method
Ⅴ. 결 론
제조상의 결함으로 인해서 이미지 센서는 손상된 화소를 영구적으로 가지고 있으며, 이미지 센서 시장 점유율 1위인 Sony는 80ppm 이하의 결함을 가지는 이미지 센서는 양품으로 판정한다. 양품 이미지 센서에 잔존하는 결함은 임펄스 잡음으로 모델링되기 때문에, 중간값 필터를 사용해서 효과적으로 제거할 수 있다. 그러나 중간값 필터를 모든 화소에 대해서 적용하면, 영상의 선예도가 떨어지므로, 임펄스 잡음에 대해서만 적용하는 것이 바람직하다.
본 논문에서는 기존에 제안했던 적응적 임펄스 잡음 제거 알고리즘의 성능을 더 향상시키기 위해서, 개선된 중간값 필터 구조를 제안한다. 첫 단계에서는 산탄잡음의 특성을 이용하여 잡음과 정상 신호를 분류한다. 잡음으로 분류된 화소에 대해서는 3x3 영역 내에서 수평수직 방향의 5개의 원소로만 구성된 중간값 필터와 대각선 방향의 5개의 원소로 구성된 중간값 필터의 결과와, 원 데이터 간에서 중간값을 취함으로써 제거한다. 제안한 방법은 범용 중간값 필터와 비교할 때, 6.92dB 이상의 성능 향상을 보여준다.
9개의 데이터에 대한 중간값 계산은 28회의 비교 연산이 필요하지만, 5개의 데이터에 대해서는 10회, 3개의 데이터에 대해서 3회가 각각 필요하다. 따라서 제안한 적응적 중간값 필터링을 위해서는 모두 23회의 비교 연산이 필요하므로, 28회의 비교 연산이 필요한 일반적인 3×3 중간값 필터링에 비해서 비교 연산의 수가 17.8%가 줄어든다.
References
- Bryce E. Bayer, "Color imaging array", US patent 3971065.
- C. M. Kyung, "Theory and applications of smart cameras", Springer. pp. 21-45, July 2014.
-
Z. Liu, T. Park, H. S. Park, and N. S. Kim, "Ultra-low-power image signal processor for smart camera applications", Electronic Letters, Vol. 51, No. 22, pp. 1778-1780, Oct. 2015.
[https://doi.org/10.1049/el.2015.1924]
-
B. K. Gunturk, J. Glotzbach, Y. Altunbasak, R. W. Schafer, and R.M. Mersereau, "Demosaicking: color filter array interpolation", IEEE Signal Processing Magazine, Vol. 22, No. 1, pp. 44-54, Jan. 2005.
[https://doi.org/10.1109/MSP.2005.1407714]
-
R. D. Gow, D. Renshaw, K. Findlater, L. Grant, S. J. McLeod, J. Hard, and R. L. Nicol, "A comprehensive tool for modeling CMOS image-sensor-noise performance", IEEE Trans. on Electron Devices, Vol. 54, No. 6, pp. 1321-1329, Jun. 2007.
[https://doi.org/10.1109/TED.2007.896718]
- Sony, IMX224LQR: Diagonal 6.09 mm (type 1/1.8) CMOS solid-state image sensor with square pixel for color cameras, preliminary datasheet, Sep. 2013.
-
Hyun-Sang Park, "A low-complexity median filter for reducing impulse noise in CMOS image sensor", Journal of KIIT, Vol. 15, No. 9, pp. 113-119, Oct. 2017.
[https://doi.org/10.14801/jkiit.2017.15.10.113]
- "Dataset of standard 512x512 grayscale test images", http://decsai.ugr.es/cvg/CG/base.htm, . [accessed: Dec. 12. 2017]
1991년 2월 : 한국과학기술원 전기및전자공학과(공학사)
1993년 8월 : 한국과학기술원 전기및전자공학과(공학석사)
1999년 8월 : 한국과학기술원 전기및전자공학과(공학박사)
2005년 2월 ~ 현재 : 공주대학교 전기전자제어공학부 교수
2007년 6월 ~ 2010년 2월 : 한국전자통신연구원 초빙연구원
2005년 12월 ~ 2013년 12월 : 삼성전자종합기술원 자문교수
관심분야 : 영상처리, 카메라신호처리, ISP, 멀티미디어 SoC