다중 사용자 MISO 간섭 채널에서 물리 계층 보안을 고려한 간단한 프리코딩 기법
초록
본 논문은 다중 사용자 다중 입력 단일 출력 (MISO) 간섭 채널에서 복수의 도청자가 존재하는 경우에, 보안 채널 수율을 향상시키기 위한 간단한 프리코딩 벡터 설계 기법을 제안한다. 제안하는 기법에서는 보안 채널 수율을 최적화하는 문제에 대해 다루었으며, 수학식으로 주어지는 분석해를 구하는 것을 목표로 하였다. 이를 위해서 신호대 누수 잡음비 (SLNR) 기반으로 프리코딩 벡터를 설계하는 방법을 제시한다. 구체적으로는, 도청자가 정보 신호를 전혀 검출할 수 없도록 도청 채널 수율을 완전히 제거하면서, 송신단-수신단 링크 간의 채널 수율을 최대화시키도록 프리코딩 벡터를 설계한다. 성능 검증을 위하여 모의실험을 수행하였으며, 송신 안테나 개수, 송신단-수신단 링크 개수, 도청자 수 간에 특별한 조건식을 만족하지 않는 환경에서는, 제안하는 기법이 모든 신호대 잡음비 범위에서 기존 기법보다 더 우수한 보안 채널 수율을 나타낸다는 것을 제시한다.
Abstract
In this paper, we propose a simple precoding vector design scheme for multi-user multiple-input single-output (MISO) interference channel when there are multiple eavesdroppers. We aim to obtain a mathematical closed-form solution of the secrecy rate optimization problem. For this goal, we design the precoding vector based on the signal-to-leakage plus noise ratio (SLNR). More specifically, the proposed precoding vector is designed to completely eliminate a wiretap channel capacity for refraining the eavesdroppers from detecting the transmitted information, and to maximize the transmitter-receiver link achievable rate. We performed simulation for the performance investigation. Simulation results show that the proposed scheme has better secrecy rate than the conventional scheme over all signal-to-noise ratio (SNR) range even though the special condition among the numbers of transmit antennas, transmitter-receiver links, and eavesdroppers is not satisfied.
Keywords:
interference channel, MISO, precoding vector, secrecy rate, physical layer securityⅠ. 서 론
다중 사용자 간섭 채널 환경에서는 복수의 송신단이 동일한 주파수와 시간 자원을 사용해서 각각의 수신단에게 정보 데이터를 전송한다[1][2]. 임의의 송신단이 전송한 신호는 목표로 하는 수신단 외에 다른 수신단에서도 수신이 되며, 이 신호는 간섭 신호로 작용한다. 수신단에 존재하는 간섭 신호는 정보 데이터 검출 성능을 크게 저하시키기 때문에, 간섭 신호를 줄이기 위한 연구는 매우 중요하다. 간섭 신호를 송신단에서 줄이는 가장 효과적인 방법 중의 하나는 다중 안테나를 사용하여 송신단 프리코딩 기법을 적용하는 것이다[3].
한편, 도청자가 존재하는 도청 채널 환경에서 도청자는 송신단이 수신단에 전송한 데이터를 도청하려고 시도한다[4]. 도청이 불가능하도록 하는 방법 중에 가장 오래되고 일반적인 방법은 통신 시스템의 상위 계층에서 암호화 기법을 적용하는 것이다. 그러나 암호를 해독하는 기술이 발전함에 따라 암호화 기술도 복잡해지고 필요한 계산량도 매우 크게 증가하는 단점이 발생하고 있다. 이러한 문제를 해결하기 위하여, 최근에는 물리 계층에서 보안 기술을 적용하는 방법에 대한 연구가 많이 진행되고 있다[5]. 물리 계층 보안 기술을 적용하는 방법 중의 하나는, 송신단에서 다중 안테나 프리코딩을 적용하는 것이다. 이 때, 도청자의 채널 수율(Achievable rate)을 크게 줄여주고, 보안 채널 수율(Achievable secrecy rate)을 최대화시키도록 프리코딩 벡터를 설계하는 것이다.
도청자가 존재하는 다중 사용자 간섭 채널 환경에서 보안 채널 수율은 모든 송신단의 프리코딩 벡터들의 함수이다[6][7]. 보안 채널 수율을 최대화시키도록 프리코딩 벡터들을 설계하기 위해서는 모든 송신단에 대한 프리코딩 벡터들을 동시에 설계해야 되고, 또한 보안 채널 수율 함수는 모든 프리코딩 벡터들에 대한 볼록 함수(Convex function)가 아니기 때문에 관련된 최적화 문제에 대한 수학적 분석해를 구하는 것은 매우 어렵다. 따라서 대부분의 기존 논문들은 반복 기법을 사용하고, CVX와 같은 최적화 문제 해결 소프트웨어를 사용하여 최적해를 구하는 방법들을 제시하고 있다[7][8]. 그러나 이러한 방법들은 매우 높은 계산량을 필요로 하고, 최적화 문제에 대한 수학적 분석해를 얻는 것이 불가능하다는 단점이 발생한다.
프리코딩 벡터를 설계하기 위해 보안 채널 수율을 비용 함수로 사용하고, 최적화 문제에 대한 수학적 분석해를 구하는 기존 방법들 중의 하나는 송신단에서 TZF(Transmit Zero-Forcing) 기술을 적용하는 것이다[8][9]. 그러나 TZF 기법에서는 부가 잡음을 고려하지 않고 프리코딩 벡터를 설계하기 때문에, 간섭 신호보다 부가 잡음이 상대적으로 큰 경우에는, TZF 기법의 보안 채널 수율 성능이 저하되는 현상이 발생한다.
또한, TZF 기법으로 간섭 신호와 도청자 수신 신호를 완전히 제거하기 위해서는 송신 안테나 개수, 송신단-수신단 링크 개수, 도청자 수 간에 특별한 제약 조건을 만족시켜야 된다. 그러나 송신 안테나의 개수가 충분히 많지 않아서 이러한 조건을 만족시키지 못하는 경우에는 일반적으로 TZF 기법을 적용할 수 없으며, TZF 기법을 변형해서 적용하게 되면 간섭 신호가 큰 영향을 줘서 보안 채널 수율이 크게 감소하는 문제가 발생한다.
본 논문에서는 기존의 TZF 기법의 단점을 보완하기 위하여, 신호대 누수잡음비(SLNR, Signal-to-Leakage plus Noise Ratio)[10] 기반의 프리코딩 설계 기법을 제안한다. 송신단에서 보낸 신호가 목표 수신단이 아닌 다른 수신단에 도달하는 수신 신호들의 전력 합을 누수 신호라고 부른다[10]. 임의의 송신단에 대한 SLNR 함수는 그 송신단에서 적용하는 프리코딩 벡터만의 함수이기 때문에, 각각의 프리코딩 벡터들을 개별적으로 설계할 수 있는 장점이 있다. 제안하는 프리코딩 벡터 설계기법에서는 도청자의 채널 수율이 완전히 제거되도록 하면서, 송신단-수신단 링크 간의 채널 수율은 최대가 되도록 프리코딩 벡터를 설계한다. 그리고 제안 기법은 송신 안테나 개수, 송신단-수신단 링크 개수, 도청자 수 간에 어떠한 특별한 제약 조건도 필요로 하지 않고, 모든 경우에 대해 적용이 가능하다.
제안 기법의 성능을 검증하기 위하여, 그 특별한 제약 조건을 만족하는 경우와 만족하지 못하는 경우에 대해서 모의실험을 수행하였다. 특별 제약 조건을 만족하는 경우에는 제안 기법과 기존 기법이 유사한 성능을 나타내지만, 특별 제약 조건을 만족시키지 못하는 환경에서는 제안하는 기법이 모든 신호대 잡음비(SNR, Signal-to-Noise Ratio) 범위에 대해서 기존 기법보다 더 우수한 보안 채널 수율을 얻을 수 있다는 것을 제시한다.
Ⅱ. 시스템 모델
그림 1은 본 논문에서 고려하는 다중 사용자 MISO(Multiple Input Single Output) 간섭 도청 채널에 대한 시스템 모델을 보여준다.
이 그림에서 TX와 RX는 각각 송신단과 수신단을 나타내며, EV는 도청자를 의미한다. 고려하는 시스템에서는 K개의 송신단-수신단 링크가 존재하고, J명의 도청자가 존재한다. 송신단은 N개의 송신 안테나를 갖는다고 가정하고, 수신단 및 도청자는 각각 한 개의 수신 안테나를 갖는다고 가정한다. 송신단 m과 수신단 k간의 채널은 사이즈가 N×1인 벡터 hm,k로 표현되며, 송신단 m과 도청자 j 간의 채널은 사이즈가 N×1인 벡터 gm,j로 표현된다.
송신단 k가 수신단 k에게 전송하는 데이터 심볼을 sk라고 표현하면, sk는 평균이 0이고 분산이 1인 복소수 정규 분포를 갖는다고 가정한다. 송신단 k는 sk를 전송하기 위하여, 사이즈가 N×1인 프리코딩 벡터 wk를 적용한다고 가정한다. 이 때, ∥wk∥=1이라는 전송 전력 제한 조건을 만족한다고 가정한다.
수신단 k에서의 수신 신호는 다음과 같이 쓸 수 있다.
| (1) |
이 식의 우변에서 첫 번째 항은 바람직한 신호를 나타내고, 두 번째 항은 사용자 간의 간섭 신호를 나타낸다. 또한, zk는 평균이 0이고 분산이 인 백색 가우시간 부가잡음을 나타낸다.
한편, 도청자 j에서의 수신 신호는 다음과 같이 쓸 수 있다.
| (2) |
여기에서 nj는 평균이 0이고 분산이 인 백색 가우시간 부가잡음을 나타낸다.
수신단 k에서의 수신 신호대 간섭 잡음비(SINR, Signal-to-Interference plus Noise Ratio)는 다음과 같이 주어진다.
| (3) |
따라서 송신단 k와 수신단 k간의 채널 수율 Γk는 다음과 같이 쓸 수 있다[7].
| (4) |
송신단 k와 도청자 j에 대한 채널 수율 은 다음과 같이 주어진다[7].
| (5) |
따라서 송신단 k와 수신단 k간의 대한 보안 채널 수율(Secrecy rate)은 다음과 같이 주어진다.
| (6) |
이제 보안 채널 수율을 최대화시키도록 프리코딩 벡터들을 설계하는 문제는 다음과 같이 표현할 수 있다.
| (7) |
보안 채널 수율 Qk는 모든 송신단 프리코딩 벡터들의 함수이고, 또한 볼록 함수(Convex function)가 아니기 때문에, Qk를 최대화시키는 프리코딩 벡터들을 구하는 문제에 대한 수학적 분석해를 구하는 것은 불가능하다.
최적화 문제 (7)에 대한 준최적(Suboptimal)의 분석해를 구하는 방법은 송신단에서 TZF 프리코딩 기법을 적용하는 것이다. 이 때, 간섭 신호를 제거하고, 도청이 불가능하도록 하기 위하여 다음 두 조건들을 만족하도록 프리코딩 벡터를 설계한다.
| (8) |
이처럼 TZF 프리코딩 기법을 적용하면, 간섭 신호 및 도청 채널 수율을 완전히 제거할 수 있고, 수학적 분석해를 구할 수 있는 장점이 있다. 그러나 TZF 기법은 부가잡음을 고려하지 않고 설계하는 기법이기 때문에, SNR이 낮은 경우에는 전체 성능이 저하되는 현상이 발생한다. 또한, 조건식 (8)을 만족하기 위해서는 송신단 안테나 개수 N, 송신단-수신단 링크 개수 K, 도청자 수 J 간에 다음 조건식을 만족해야 된다.
| (9) |
그러나 송신 안테나 개수가 적거나 송신단-수신단 링크 개수 및 도청자 수가 많은 경우에는 조건식 (9)를 만족시키지 못하기 때문에, TZF 기법을 적용하는 것은 일반적으로 불가능하다.
Ⅲ. 제안하는 프리코더 설계 기법
이 장에서는 기존의 TZF 기법의 문제점을 해결하기 위하여, SLNR 기반의 프리코딩 벡터 설계 방법을 제안한다.
송신단 k에서 수신단 k로 전송되는 수신 신호 세기는 로 주어진다. 그리고 송신단 k에서 전송한 신호가 다른 수신단에 전송되는 누수 신호들의 전력 합은 에 의해 주어진다.
| (10) |
SINR은 모든 사용자들의 프리코딩 벡터들의 함수이기 때문에 SINR을 최대화시키기 위해서는 모든 사용자들의 프리코딩 벡터들을 동시에 설계해야 되고, 이로 인해서 설계 복잡도가 매우 커지는 단점이 있다. 그러나 SLNR은 단지 사용자 k만의 프리코딩 벡터의 함수이기 때문에, 사용자 k의 프리코딩 벡터만 독립적으로 설계하면 된다.
그리고 송신단 k에서 전송한 신호가 모든 도청자에게 전혀 전달되지 않도록 하기 위해서는 프리코딩 벡터 wk가 gk,j에 직교해야 되며, 다음과 같은 조건식으로 표현할 수 있다.
| (11) |
따라서 본 논문에서 제안하는 프리코딩 벡터 설계 기법은 다음 최적화 문제로 표현할 수 있다.
| (12) |
송신단 k로부터 모든 도청자들에 대한 채널을 결합한 행렬을 Gk = [gk,1,...,gk,J]H 라고 정의하자. 그리고 Gk에 대한 특이값 분해(SVD, Singular Value Decomposition)를 다음과 같이 표현하자.
| (13) |
여기에서 Uk는 크기가 K×K인 유니터리(Unitary) 행렬이고, Σk는 직각 대각행렬이고, Vk는 크기가 N×N인 유니터리 행렬을 나타낸다. 또한, Vk = [Vk,1 Vk,2]로 표현하면, Vk,1은 0이 아닌 특이값에 해당하는 특이 벡터들의 집합이고, Vk,2는 값이 0인 특이값에 해당하는 특이 벡터들의 집합이다. 즉, Vk,2는 Gk의 널 공간(Null space)에 대한 기저 벡터들을 의미하며, 행렬의 사이즈는 N×(N-K)이다. 따라서 도청 채널 gk,j, j = 1,...,J,에 직교하는 프리코딩 벡터들은 다음과 같이 표현할 수 있다.
| (14) |
여기에서 ck는 크기가 (N-K)×1이고, ∥ck∥= 1인 벡터이다.
이제 식 (14)를 식 (12)에 대입하면, 최적화 문제는 다음과 같이 다시 쓸 수 있다.
| (15) |
또한, 을 이용하면, 이 식을 다음과 같이 다시 쓸 수 있다.
| (16) |
이 최적화 문제에 대한 해는 다음과 같이 구할 수 있다[11].
| (17) |
여기에서 max_geig(A,B)는 행렬 펜슬 (A,B)의 가장 큰 고유 값에 해당하는 고유 벡터를 나타낸다. 식 (14)와 (17)을 이용하면, 본 논문에서 제안하는 프리코딩 벡터를 얻을 수 있다.
Ⅳ. 모의실험
본 장에서는 제안하는 프리코딩 설계 기법의 성능을 검증하기 위하여 모의실험 결과들을 제시한다. 제안하는 기법과 기존의 TZF 기법 간의 성능을 비교하기 위하여 보안 채널 수율을 비교한다. 송신단 m과 수신단 k 간의 채널 벡터 hm,k, 그리고 송신단 m과 도청자 j 간의 채널 벡터 gm,j은 각각 평균이 0이고 분산이 1인 레일레이 평탄 페이딩 (Rayleigh flat fading) 채널 모델을 갖는다고 가정하였다. 실험을 위하여 1000개의 독립적인 채널을 발생시켰으며, 각각의 결과들을 평균함으로써 최종 결과들을 도출하였다.
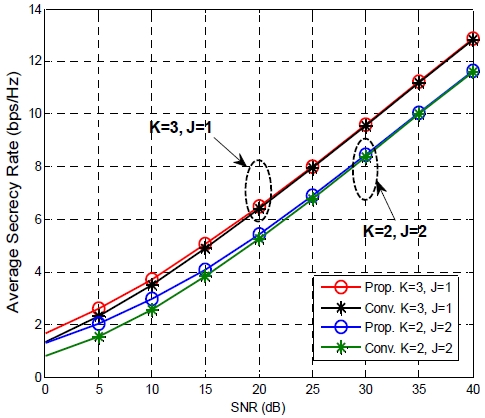
그림 2는 식 (9)에서 주어진 제약 조건을 만족하는 경우에 대한 평균 보안 채널 수율 결과를 나타낸다. 송신 안테나 개수는 N = 4이고, TX-RX 링크의 개수 K와 도청자 수 J의 조합은 (K,J) = (3,1), (2,2)을 사용하였다. 그리고 ‘Prop.’과 ‘Conv.’는 각각 제안 기법과 기존 기법의 성능을 나타낸다. 평균 보안 채널 수율을 얻기 위하여 모든 송신단-수신단 링크에 대한 보안 채널 수율 결과들을 평균하였다. 이 그림으로부터 SNR이 낮은 경우에는 제안하는 기법이 기존 TZF 기법보다 약간 성능이 우수하고, SNR이 높은 경우에는 두 기법의 성능이 비슷하다는 것을 알 수 있다.
SNR이 낮은 경우는 부가 잡음의 세기가 간섭 신호보다 더 큰 경우를 나타내며 기존 TZF 방법은 부가 잡음을 고려하지 않고 프리코딩 벡터를 설계하기 때문에 낮은 SNR에서 성능이 저하되는 현상이 발생한다.
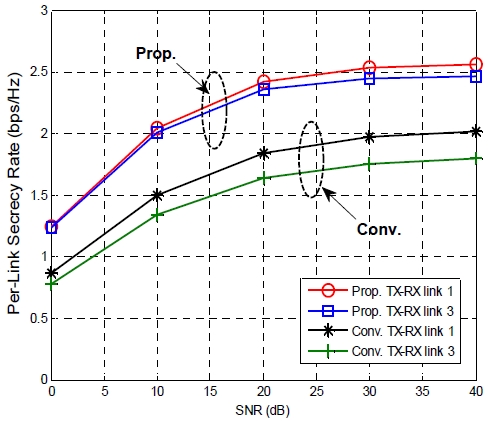
그림 3은 식 (9)에서 주어진 조건을 만족하지 못하는 경우에 대해서 각 송신단-수신단 링크에 대한 보안 채널 수율 결과를 나타낸다. 송신 안테나 개수는 N = 4, 송신단-수신단 링크 개수는 K = 3, 도청자 수는 J = 2이다. 이 경우는 식 (9)에서 주어진 조건을 만족시키지 못하기 때문에, 일반적으로는 기존의 TZF 기법을 적용하는 것이 불가능하다.
그러나 이 환경에서도 기존의 TZF 기법을 적용하가 위하여, TFZ 프리코딩 벡터가 송신단과 수신단 간의 채널 벡터 hm,k 중의 일부에 대해서만 직교하도록 설계하였다. K = 3이므로, 3개의 송신단-수신단 링크가 존재하며, 이 중에서 링크 1과 링크 3에 대한 결과를 보여준다. 이 그림으로부터 모든 SNR 범위에 대해서 제안하는 기법이 기존 TZF 기법보다 더 우수한 보안 채널 수율 성능을 갖는다는 것을 알 수 있다. 또한, 제안하는 기법은 링크 1과 링크 3 간의 성능이 비슷하지만 기존 TZF 기법은 두 링크 간에 성능 차이가 많이 난다는 것을 알 수 있다.
Ⅴ. 결 론
본 논문에서는 도청자가 존재하는 경우에 다중 사용자 MISO 간섭 채널을 고려하였으며, 보안 채널 수율 성능을 향상시키기 위한 프리코딩 벡터 설계 기법을 제안하였다. 제안하는 기법에서는 보안 채널 수율 성능 최적화 문제에 대한 수학적 분석해를 구하기 위하여 SLNR 기반으로 프리코딩 벡터를 설계하였다. 이 때, 도청자의 채널 수율은 완전히 제거되도록 하였으며, 송신단-수신단 링크의 채널 수율은 최대화되도록 프리코딩 벡터를 설계하였다. 그리고 제안하는 기법은 송신 안테나 개수, 송신단-수신단 링크 개수, 도청자 수 간에 특별한 제약 조건이 필요로 하지 않는다는 장점이 있다. 모의실험을 통하여 제안 기법과 기존 TZF 기법 간의 보안 채널 수율 성능을 비교하였으며, 그 특별한 제약조건을 만족하지 않는 경우에는 모든 SNR에 대해서 제안하는 기법이 기존 TZF 기법보다 훨씬 우수한 보안 채널 수율 성능을 나타낸다는 것을 보였다.
Acknowledgments
이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임. (No. 2016R1D1A3B03935210)
References
-
J. Choi, "Interference alignment over lattices for MIMO interference channels", IEEE Commun. Letters, Vol. 15, No. 4, pp. 374-376, Apr. 2011.
[https://doi.org/10.1109/LCOMM.2011.012511.101576]

-
C. Wang, "Degrees of freedom characterization: The 3-user SISO interference channel with blind interference alignment", IEEE Commun. Letters, Vol. 18, No. 4, pp. 757-760, May 2014.
[https://doi.org/10.1109/LCOMM.2014.030714.140177]

-
S. H. Jung and S. H. Kim, "Pre-coding improvement research for efficiency of channel capacity in MIMO systems", Journal of KIIT, Vol. 11, No. 11, pp. 69-74, Nov. 2013.
[https://doi.org/10.14801/kiitr.2013.11.11.69]

-
X. He and A. Yener, "MIMO wiretap channels with unknown and varying eavesdropper channel states", IEEE Trans. Inform. Theory, Vol. 60, No. 11, pp. 6844-6869, Nov. 2014.
[https://doi.org/10.1109/TIT.2014.2359192]

-
A. Mukherjee et al, S. A. A. Fakoorian, J. Huang, and A. L. Swindlehurst, "Principles of physical layer security in multiuser wireless networks: A survey", IEEE Comm. Surv. Tutorials, Vol. 16, No. 3, pp. 1550-1573, Jul. 2014.
[https://doi.org/10.1109/SURV.2014.012314.00178]

-
M. Cheng, J.-B. Wang, and J. Cheng, "A new lower bound based secure beamforming in MISO communication networks", IEEE Comm. Letters, Vol. 23, No. 9, pp. 1474-1478, Sept. 2019.
[https://doi.org/10.1109/LCOMM.2019.2923212]

-
Q. Li, and W.-K. Ma, "Optimal and robust transmit designs for MISO channel secrecy by semidefinite programming", IEEE Trans. Signal Proess., Vol. 59, No. 8, pp. 3799-3812, Aug. 2011.
[https://doi.org/10.1109/TSP.2011.2146775]

-
S. Jin, X. Wang, Z. Li, K.-K. Wong, Y. Huang, and X. Tang, "On massive MIMO zero-forcing transceiver using time-shifted pilots", IEEE Trans. Vehic. Technol., Vol. 65, No. 1, pp. 59-74, Jan. 2016.
[https://doi.org/10.1109/TVT.2015.2391192]

-
J. Zhu, R. Schober, and V. K. Bhargava, "Linear precoding of data and artificial noise in secure massive MIMO systems", IEEE Trans. Wireless Comm., Vol. 15, No. 3, pp. 2245-2261, Mar. 2016.
[https://doi.org/10.1109/TWC.2015.2500578]

-
M. Sadek, A. Tarighat, and A. H. Sayed, "A leakage-based precoding scheme for downlink multi-user MIMO channels", IEEE Trans. Wireless Comm., Vol. 6, No. 5, pp. 1711-1721, May 2007.
[https://doi.org/10.1109/TWC.2007.360373]

- R. A. Horn and C. R. Johnson, "Matrix Analysis", Cambridge, U. K.: Cambridge Univ. Press, 1993.

1997년 2월 : KAIST 전기 및 전자공학과 (공학사)
1999년 2월 : KAIST 전기 및 전자공학과 (공학석사)
2010년 2월 : KAIST 전기 및 전자공학과 (공학박사)
2004년 11월 ~ 2013년 2월 : 한국전자통신연구원 선임연구원
2013년 3월 ~ 현재 : 공주대학교 부교수
관심분야 : 이동통신, 단말간 직접통신 (D2D), 다중 안테나 기술 (MIMO), 프리코더 설계, 인공지능