직교공간변조 시스템을 위한 유클리디안 거리 기반의 복잡도 감소 전력 할당 알고리즘

Ⅰ. 서 론

공간변조(SM, Spatial Modulation) 전송 기술은 다중 송수신 안테나를 사용하는 MIMO(Multiple-Input Multiple Output) 무선통신 시스템에서 정보를 전달하는 수단으로 전통적인 전송 심볼 신호 이외에 송신안테나의 인덱스를 통해서도 추가적인 정보를 전송할 수 있는 기술이다[1][2]. 공간변조가 하나의 송신 안테나 만을 활성화 하고 수신기의 복잡성을 낮추면서 스펙트럼 효율(Spectral efficiency)을 증대시킬 수 있음에도 불구하고 기존의 공간변조의 스펙트럼 효율을 더욱 증대시키기 위해서 새로운 직교공간변조(QSM, Quadrature Spatial Modulation) 전송 기술이 최근에 개발되었다[3]. 직교공간변조 시스템은 전송하고자하는 심볼의 실수부와 허수부를 전송하기 위해서 두 개의 직교 공간을 이용한다.

기존의 공간변조 시스템의 성능을 개선하기 위해서 송신안테나 선택 기법들이 발표되었다[4][5]. [6]과 [7]에서는 채널 페이딩에 의한 불리한 통신 환경을 극복하기 위해 공간변조에 전력 할당(PA, Power Allocation) 기법들이 적용되었다. 한편, [8]에서 다양한 송신안테나 선택 알고리즘들이 직교공간변조 시스템의 오류 성능을 향상시키기 위해서 연구되었다. [9]에서는 전력 할당 기법이 결합된 직교공간변조 시스템에 대한 연구가 최근에 진행되었다. 그러나 [9]에서 제안된 최소 유클리디안 거리(ED, Euclidean distance) 기반의 전력 할당최적화 알고리즘은 엄청난 계산량을 요구하고 있다. 따라서 복잡도를 낮춘 전력 할당 알고리즘을 개발할 필요가 있다. 본 논문에서는 복잡도를 줄이기 위해서 유클리디안 거리 기반의 최적화 기준식을 수정하고자 한다. 제안된 전력 할당 알고리즘의 비트 오류 확률(BER, Bit Error Rate)과 복잡도를 ES(Exhaustive Search) 기반의 알고리즘과 비교 평가한다.

본 논문의 구성을 다음과 같다. 2장은 송신 전력이 할당된 직교공간변조에 대하여 설명한다. 3장에서는 복잡도를 감소시키는 유클리디안 거리 기반의 전력 할당 알고리즘을 제안한다. 4장에서는 시뮬레이션 결과를 통해 ES 기반의 최적화 알고리즘과 제안된 전력 할당 알고리즘의 오류 성능을 비교 분석한다. 5장에서는 결론에 대해 기술한다.

Ⅱ. 송신 전력 할당을 기반으로 한 QSM

본 논문에서는 N_T개의 송신안테나와 N_R개의 수신안테나로 구성된 MIMO 채널에서 송신 전력 할당을 채택하는 직교공간변조 시스템을 고려한다[3][9]. 매 순간마다 입력 정보 비트들은 log₂N_T , log₂N_T 그리고 log₂M과 같이 세 개의 부분으로 분할하여 전송된다. 여기서 M은 전송 신호의 심볼 변조 차수를 나타낸다. 두 개의 log₂N_T 크기에 해당하는 첫 번째 및 두 번째 비트 집합들은 하나의 신호 심볼 x(=x_R+jx_I) 실수부 x_R과 허수부 x_I를 각각 전송하기 위한 두 개의 공간 변조된 심볼 $$ x_R^{m_R}$$와 $$ x_I^{m_I}$$를 만든다. 여기서 심볼 x는 log₂M 의 마지막 비트들에 의해 변조되었고, m_R(=1,2,…,N_T)과 m_I(= 1,2,…,N_T) 는 두 개의 활성화된 송신안테나 인덱스를 표시한다. 직교공간변조 시 한 개의 송신안테나가 활성화될 때 전력 할당 인자 $$ p_m^{\left(g\right)}$$(∈(0,1])(m = 1,2,…,N_T, g = 1,2,…,G)가 변조된 심볼의 가중치로서 적용되고 $$ \sum _{m=1}^{N_T}{p}_m^{{\left(g\right)}^2}=N_T$$을 만족하도록 한다. 여기서 G는 전력 할당 인자로서 사용될 수 있는 전체 개수를 나타내고, 피드백 비트 개수에 의해 결정된다. 만약 두 개의 송신 안테나가 활성화될 때는 전력 할당 인자 $$ p_{m_R}^{\left(g\right)}$$ 와 $$ p_{m_I}^{\left(g\right)}$$가 사용되고, m_R ≠ m_I 와 $$ p_{m_R}^{{\left(g\right)}^2}+p_{m_I}^{{\left(g\right)}^2}+\sum _{\begin{array}{c}m=1\\ m\ne m_R,m_I\end{array}}^{N_T}{p}_{m_R}^{{\left(g\right)}^2}=N_T$$가 만족된다.

본 논문에서는 N_R×2와 N_R×4 직교공간변조 전력 할당 시스템을 위해서 표 1, 표 2, 그리고 표 3에서 주어진 전력 할당 인자들을 사용한다[9]. 여기서, 선택된 인자 값들은 시뮬레이션에서 고려하는 송신안테나의 최대 수가 4개이므로 균일 분포를 따르는 값들로 구성된 집합 {$$ \sqrt{0.4}$$, $$ \sqrt{0.8}$$, $$ \sqrt{1.2}$$, $$ \sqrt{1.6}$$}를 이용한다.

Table 1.

Power allocation factors for NR×2 QSM with 2 bits feedback

Table 2.

Power allocation factors for NR×4 QSM with 3 bits feedback

Table 3.

Power allocation factors for NR×4 QSM with 4 bits feedback

그러면 g 번째 전력 할당 인자 후보에 해당하는 직교공간변조된 신호 벡터는 다음과 같이 표현된다[2].

여기서 $$ {\overline{e}}_{m_R}$$와 $$ {\overline{e}}_{m_I}$$는 N_T×N_T 크기의 단위행렬의 m_R 번째와 m_I 번째 열(Column)벡터들을 나타낸다. 전력 할당된 신호 벡터 $$ {\overline{z}}^{\left(g\right)}$$는 N_R×N_T 크기의 무선 MIMO 채널 H을 통해 전송된다. 행렬 H의 모든 원소들은 평균은 0이고 분산 값은 1인 복소 가우시안 i.i.d.(independent and identically distributed) 랜덤 변수이다. 그리하여 g번째 전력 할당 인자 후보에 해당하는 N_R×1 크기의 수신 신호 벡터는 다음과 같이 주어진다.

여기서 $$ \overline{w}={\left[w_1 w_2 \cdots w_{N_R}\right]}^T$$는 N_R×1 크기의 평균이 0이고 분산 값이 N₀인 i.i.d. 복소 AWGN(Additive White Gaussian Noise) 잡음 벡터이다.

활성화된 송신안테나 인덱스와 전송 심볼을 공동으로 한꺼번에 추정하기 위해서 우선적으로 모든 가능한 QSM 심볼에 대해서 최적의 ML(Maximum-Likelihood) 수신기를 다음과 같이 수행한다[9].

여기서 ∥ㆍ∥_F 는 Frobenius 놈(Norm) 연산을 의미한다. ML 수신기의 오류 성능을 평가하기 위하여 모든 가능한 QSM 심볼과 전력 할당 인자 후보군에 대해 최소 유클리디안 거리 d_min를 최대화하고자 한다. 그리하여 ES 기반의 ED 기반의 전력 할당 알고리즘(ED-PA-ES)은 다음과 같이 정의된다[6].

여기서 $$ {\overline{h}}_m$$은 행렬 H의 m(= m_R,n_R,m_I,n_I) 번째 열벡터들을 나타내고, u ≠ v 혹은 m_R ≠ n_R 이고, m_R,n_R,m_I,n_I∈{1,2,…,N_T}이다.

(4)의 ED-PA-ES 최적화 문제는 다음과 같이 표현될 수 있다.

여기서 D(g)는 채널 행렬 H 과 표 1과 표 2에 주어진 인덱스 g에 해당하는 전력 할당 인자들과 모든 가능한 QSM 심볼 벡터들에 의해 계산된 N_T×N_T 크기의 행렬이다. 정방행렬의 대각원소에 해당하는 m = n에 대해 D(g)의 (m,n)번째 원소는 다음과 같이 기술된다.

여기서 u ≠ v,m_R(= m) = n_R(=n), m_I∈{1,2,…,N_T}, n_I∈{m_I,m_I+1,⋯,N_T}, m = m_R∈{1,2,…,N_T}을 만족한다. m < n에 대해서는 D(g)의 (m,n)번째 원소도 (7)과 같이 주어지고, 이때는 m_R(= m) ≠ n_R(=n), m_I∈{1,2,…,N_T}, n = n_R∈{m,m+1,…,N_T}, n_I∈{m_I,m_I+1,…,N_T}, m = m_R∈{1,2,…,N_T}을 만족된다.

계산량에 의한 복잡도 분석을 위해 [4]과 [8]에서와 비슷한 방법을 사용하여 계산한다. 본 논문에서 복소수 곱셈 대신에 실수 곱셈을 복잡도 계산에서 사용하도록 한다. 그러면 ED-PA-ES 최적화 알고리즘의 대략적인 floating point 연산량은 다음과 같이 계산된다.

여기서 $$ C_2^{N_T}$$는 이항계수이다.

Ⅲ. 복잡도가 감소된 ED 기반의 전력 할당 알고리즘

복잡도가 O(M²)에 비례하는 ED-PA-ES 알고리즘을 [8]에서 사용된 방법을 적용하여 최적화 수식을 변형하여 복잡도를 줄이고자 한다. 이렇게 감소된 복잡도(Reduced complexity)를 가진 ED 기반의 PA 알고리즘을 ED-PA-RC라 지칭한다. 심볼 $$ x_{R,v}^{n_R}$$와 $$ x_{I,v}^{n_I}$$이 주어졌다는 조건 하에 m = n인 경우, (7)의 수식은 다음과 같이 표현될 수 있다.

여기서 u ≠ v, m_R(= m) = n_R(= n), m_I∈{1,2,..., N_T}, n_I∈{m_I,m_I+1,…,N_T}, m = m_R∈{1,2,..., N_T}을 만족한다. m < n에 대해서는 D(g)의 (m,n)번째 원소도 (9)와 같이 주어지고, 이때는 m_R(= m) ≠ n_R(= n), m_I∈{1,2,…,N_T}, n = n_R∈{m,m+1,…,N_T}, n_I∈{m_I,m_I+1,…,N_T}, m = m_R∈{1,2,…,N_T}을 만족한다. 또한

여기서 B_I(r₁)와 B_R(r₂)는 r₁과 r₂를 전송 QSM 심볼의 허수부와 실수부의 가장 가까운 점으로 복조하는 연산을 나타낸다. 이 때 심볼 $$ {\widehat{s}}_u$$는 $$ {\widehat{s}}_u=B_R\left(r_2\right)+j{B}_I\left(r_1\right)$$로 주어진다. 그리고 $$ {\tilde{h}}_{ab}^{\left(m,n\right)}\left(g\right)\left(a,b=\mathrm{1,2},\mathrm{3,4}\right)$$는 다음과 같이 정의된 4×4 크기 행렬의 (a,b)번째 원소이다.

여기서 $$ {\stackrel{-}{h}}_{m_R}^R\left(g\right)=Re\left({\stackrel{-}{h}}_{m_R}{p}_{m_R}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{m_R}^I\left(g\right)=Im\left({\stackrel{-}{h}}_{m_R}{p}_{m_R}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{n_R}^R\left(g\right)=Re\left({\stackrel{-}{h}}_{n_R}{p}_{n_R}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{n_R}^I\left(g\right)=Im\left({\stackrel{-}{h}}_{n_R}{p}_{n_R}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{m_I}^R\left(g\right)=Re\left({\stackrel{-}{h}}_{m_I}{p}_{m_I}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{m_I}^I\left(g\right)=ImIm\left({\stackrel{-}{h}}_{m_I}{p}_{m_I}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{n_I}^R\left(g\right)=Re\left({\stackrel{-}{h}}_{n_I}{p}_{n_I}^{\left(g\right)}\right)$$, $$ {\stackrel{-}{h}}_{n_R}^I\left(g\right)=Im\left({\stackrel{-}{h}}_{n_R}{p}_{n_R}^{\left(g\right)}\right)$$이다.

그러면 ED-PA-RC 알고리즘의 근사화된 복잡도는 다음과 같다.

그리하여 심볼 변조 차수가 클 때는 ED-PA-RC 알고리즘이 ED-PA-ES 알고리즘보다 복잡도 측면에서 더 큰 이점을 제공할 수 있다. 게다가 [4]와 [8]에서처럼 각도의 rotational symmetry 성질을 이용한다면 복잡도를 다음과 같이 더 줄일 수 있다.

Ⅳ. 시뮬레이션 결과

이 장에서는 제한된 피드백을 가진 전력 할당QSM 시스템에서 제안된 ED-PA-RC 알고리즘의 오류 성능을 Rayleigh 평탄 페이딩 채널에서 평가한다. MIMO 채널 정보가 ML 수신기에 알려져 있다고 가정한다. ML 수신기는 활성화된 안테나 인덱스와 전송 심볼을 동시에 추정한다. 시뮬레이션에서 사용된 신호 대 잡음 전력 비(SNR, Signal to Noise Ratio)는 활성화된 송신안테나로부터 전송된 전체적인 신호 전력 나누기 잡음 분산 값으로 정의한다.

그림 1은 N_T = 2와 N_R = 2를 가진 전력 할당 QSM 시스템에서 ED-PA-RC 알고리즘의 BER 성능을 보여준다. 여기서, 4-QAM을 사용하고 그리하여 스펙트럼 효율은 4 bits per channel use(4 bpcu)로 주어진다. 표 1에 주어진 전력 할당 인자들을 사용하고 이는 2비트 피드백에 해당된다. ED-PA-RC의 오류 성능은 전력 할당 없이 사용하는 기존의 QSM 시스템에 비해 상당히 개선된다는 것을 볼 수 있다. 한편 ED-PA-RC의 오류 성능은 ED-PA-ES의 오류 성능보다는 아주 근소하게 떨어진다는 것을 확인할 수 있다.

Fig. 1.

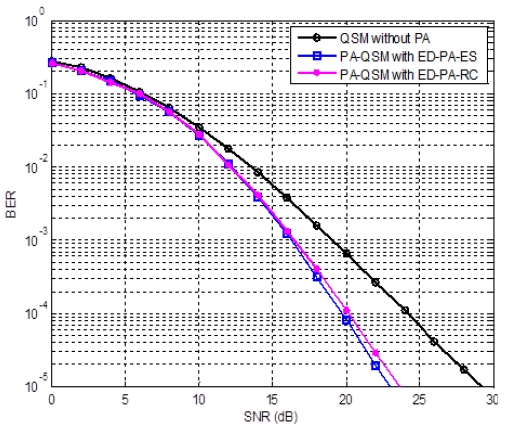
BER performance of the proposed ED-PA-RC and the ED-PA-ES for power allocated QSM and the conventional QSM without power allocation for NT = 2 and NR = 2

그림 2는 N_T = 4와 N_R = 2, 그리고 4-QAM을 사용하는 경우 오류 성능 평가가 이루어지고 있다. 여기서는 3비트 피드백을 가정하고 전력 할당 인자들은 표 2에서 주어진 값들을 사용한다. 그리하여 스펙트럼 효율은 6 bpcu로 주어진다. ED-PA-RC 알고리즘은 ED-PA-ES 알고리즘과 거의 동일한 성능을 보이고 있고, ED-PA-RC를 사용하는 전력 할당 QSM 시스템은 전력 할당 없이 사용하는 기존의 QSM 시스템보다는 엄청나게 우수한 성능을 보이고 있음을 확인할 수 있다.

Fig. 2.

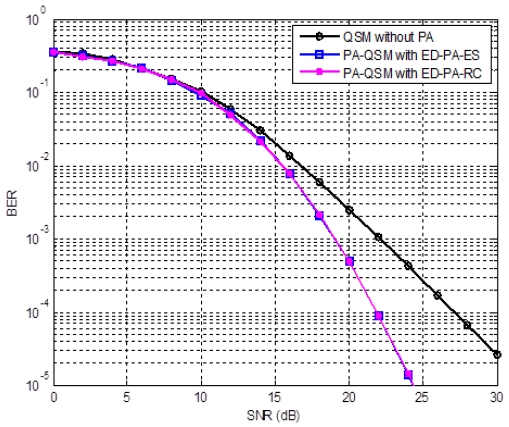
BER performance of the proposed ED-PA-RC and the ED-PA-ES for power allocated QSM and the conventional QSM without power allocation for NT = 4 and NR = 2

그림 3에서는 N_T = 4, N_R = 4, 4-QAM을 사용하는 QSM 시스템의 BER 성능 평가를 진행한다. 이 경우에는 4비트 피드백을 가정하고 표 3에서 표시된 전력 할당 인자 값들을 사용한다. 4개의 수신안테나로 주어진 시뮬레이션 조건에서도 ED-PA-RC 알고리즘과 ED-PA-ES 알고리즘은 거의 동일한 BER 결과를 나타내고 있다. 한편 ED-PA-RC 기반의 전력 할당 QSM 시스템은 전력 할당 없는 기존의 QSM 시스템보다는 우수한 성능을 보이고 있으나 성능 개선 효과는 2개의 수신안테나의 경우보다는 적음을 확인할 수 있다. 이는 전력 할당 없는 기존의 QSM 시스템에서 4개의 수신안테나에 의한 수신 다양성 이득 효과가 2개의 수신안테나의 경우보다 크기 때문이다.

Fig. 3.

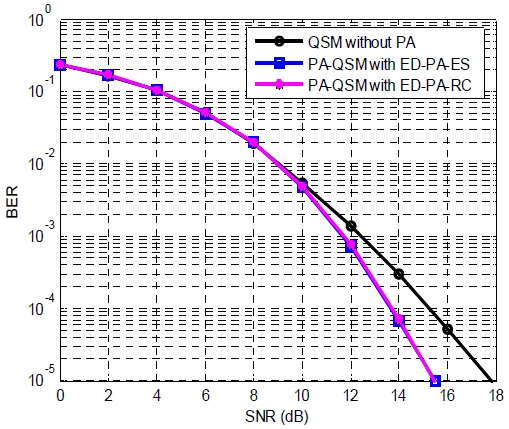
BER performance of the proposed ED-PA-RC and the ED-PA-ES for power allocated QSM and the conventional QSM without power allocation for NT = 4 and NR = 4

그림 2와 3에 해당하는 3비트와 4비트 피드백을 사용하는 경우에는 ED-PA-RC 알고리즘이 ED-PA-ES 알고리즘의 성능과 거의 유사하지만, 그림 1의 2비트 피드백인 경우에는 ED-PA-RC 알고리즘의 성능이 ED-PA-ES 알고리즘 보다 조금 떨어지는 것을 확인할 수 있다. 이는 ED-PA-RC 알고리즘이 피드백 비트수가 작은 2인 경우에는 BER 성능에 영향을 더 받아서 약간의 성능 저하가 발생하기 때문이다.

Ⅴ. 결 론

본 논문에서는 제한된 피드백을 가진 QSM 시스템에서 복잡도가 줄어든 전력 할당 알고리즘을 제안하였다. 제안된 전력 할당 알고리즘은 최소 유클리디안 거리를 최대화하는 고유의 최적화 알고리즘을 변형하여 전개하였다. 기존의 ED-PA-ES 알고리즘은 O(M²)에 비례하는 복잡도를 가지고 있는 반면에 제안된 ED-PA-RC 알고리즘은 O(M)에 비례하는 복잡도를 가지고 있음을 확인하였다. 추가적으로 Rotational Symmetry 성질을 이용하면 복잡도가 O(M/2)로 비례하도록 더욱 낮출 수 있었다. 2개의 송신안테나, 2개의 수신안테나와 2비트 피드백을 가진 QSM 시스템에서는 ED-PA-RC와 ED-PA-ES의 BER 성능 차이가 최소화가 되었다는 것을 알 수 있으며, 또한, 4개의 송신안테나, 2개의 수신안테나, 3비트 피드백과 4개의 송신안테나, 4개의 수신안테나, 4비트 피드백을 가진 QSM 시스템에서는 ED-PA-RC의 오류 성능은 ED-PA-ES와 거의 동일하다는 것을 알 수 있었다. 향후 과제로 QSM 시스템을 위한 계산량이 더욱 감소된 저-복잡도 전력 할당 알고리즘에 대한 연구가 추가적으로 필요하다.

Acknowledgments

본 논문은 동아대학교 교내연구비 지원에 의하여 연구되었음.

References

• R. Mesleh, H. Haas, S. Sinanovic, C. W. Ahn, and S. Yun, "Spatial modulation", IEEE Transactions on Vehicular Technology, Vol. 57, No. 4, pp. 2228-2241, Jul. 2008. [https://doi.org/10.1109/TVT.2007.912136]
• M. Di Renzo, H. Haas, and P. M. Grant, "Spatial modulation for multiple-antenna wireless systems: a survey", IEEE Communications Magazine, Vol. 49, No. 12, pp. 182-191, Dec. 2011. [https://doi.org/10.1109/MCOM.2011.6094024]
• R. Mesleh, S. Ikki, and H. M. Aggoune, "Quadrature spatial modulation", IEEE Transactions on Vehicular Technology, Vol. 64, No. 6, pp. 2738-2742, Jun. 2015. [https://doi.org/10.1109/TVT.2014.2344036]
• R. Rajashekar, K. V. S. Hari, and L. Hanzo, "Antenna selection in spatial modulation systems", IEEE Communications Letters, Vol. 17, No. 3, pp. 521-524, Mar. 2013. [https://doi.org/10.1109/LCOMM.2013.012213.122650]
• B. Kumbhani, R. S. Kshetrimayum, "Outage probability analysis of spatial modulation systems with antenna selection", Electronics Letters, Vol. 50, No. 2, pp. 125-126, Jan.2014. [https://doi.org/10.1049/el.2013.3466]
• Y. Xiao, Q. Tang, L. Gong, P. Yang, and Z. Yang, "Power scaling for spatial modulation with limited feedback", International Journal of Antennas and Propagation, Vol. 2013, Art. ID. 718482, 5pages, May 2013.
• P. Yang, Y. Xiao, B. Zhang, S. Li, M. El-Hajjar, and L. Hanzo, "Power allocation-aided spatial modulation for limited-feedback MIMO systems", IEEE Transactions on Vehicular Technology, Vol. 64, No. 5, pp. 2198-22199, May 2015. [https://doi.org/10.1109/TVT.2014.2339297]
• S. Kim, "Antenna selection schemes in quadrature spatial modulation systems", ETRI Journal, Vol. 38, No. 4, pp. 612-621, Aug. 2016. [https://doi.org/10.4218/etrij.16.0115.0986]
• S. Kim, "Performance of power scaling-based quadrature spatial modulation systems with limited feedback", IEEJ Transactions on Electrical and Electronic Engineering, Vol. 14, No. 9, pp. 1342-1347, Sep. 2019. [https://doi.org/10.1002/tee.22935]