허프 변환을 이용한 다표적 환경에서 동적 RCS 분리
초록
레이더를 사용하여 탄도 미사일의 기두부를 추적할 때, 표적의 주변에 있는 각종 기만체들은 표적을 추적하는 레이더의 자원 관리에 큰 부담을 준다. 이러한 부담을 줄이기 위해서 레이더에 수신된 동적 RCS 신호로부터 탄도 미사일 기두부의 신호를 분리할 수 있어야 한다. 본 논문에서는 이미지에서 직선을 추출하는 알고리즘인 허프 변환 방법을 이용하여, 레이더에 수신된 신호로부터 각각의 표적들의 동적 RCS를 분리하는 방법을 제안한다. 기두부와 기만체의 3차원 CAD 모델을 사용하여 표적들의 미세거동을 구현하였다. 또한 미세거동을 가지는 3차원 CAD로부터 표적의 동적 RCS를 계산하고 제안된 알고리즘을 적용하여 알고리즘의 성능을 검증하였다. 시뮬레이션 결과 제안된 방법은 SNR이 10dB에서 미사일 기두부와 기만체의 신호를 분리할 수 있음을 확인하였다.
Abstract
When a radar tracks the warhead of a ballistic missile, decoys of a ballistic missile put a heavy burden on the radar resource management tracking the targets. To reduce this burden, it is necessary to be able to separate the signal of the warhead from the received dynamic radar cross section (RCS) signal on the radar. In this paper, we propose the method of separating the dynamic RCS of each target from the received signal by the Hough transform which extracts straight lines from the image. The micro motion of the targets was implemented using a 3D CAD model of the warhead and decoys. Then, we calculated the dynamic RCS from the 3D CAD model having micro-motion and verified the performance by applying the proposed algorithm. Simulation results show that the proposed method can separate the signals of the warhead and decoys at the signal-to-noise ratio (SNR) of 10dB.
Keywords:
warhead, decoy, micro-Doppler, Hough transform, dynamic RCSⅠ. 서 론
탄도 미사일의 기두부는 매우 고속으로 이동하며 짧은 시간 동안 복잡한 움직임을 보이는 대표적인 초고속 고기동 표적이다. 이러한 초고속 고기동 표적들은 레이더를 사용하여 추적 및 요격이 가능하다[1][2]. 이때, 요격 미사일로부터 기두부의 생존성을 높이기 위한 방법 중 하나로 기만체들을 이용한다[3]. 이러한 상황에서 표적을 추적하는 레이더는 다수의 기두부와 기만체 모두를 추적해야 하며, 이는 레이더의 자원 관리에 큰 부담을 준다. 이러한 문제를 해결하기 위해서는 갑자기 발생한 다수의 표적들 중에서 기만체는 무시하고 기두부만을 추적하는 방법이 필요하다. 다수의 표적 중에서 기두부만을 선택적으로 추적하기 위해서는 기두부와 기만체의 신호를 분리하는 방법이 필요하다[4][5].
본 논문에서는 다표적이 포함되어 있는 신호로부터 단일 표적의 신호를 분리하는 새로운 방법을 제안한다. 본 논문과 유사한 선행 연구들 중에는 ICA(Independent Component Analysis)[6]와 PSO(Particle Swarm Optimization)[7]를 이용한 연구가 있다. ICA를 이용한 연구는 단일 표적의 미세도플러에서 ICA를 이용하여 표적의 특징을 추출하고 다양한 구분기를 이용하여 표적의 구분 성능을 비교한 연구가 있다[8]. 그리고 PSO를 이용한 연구에서는 단일 표적의 미세도플러 영상에서 PSO를 이용하여 비용함수를 최소화하는 표적의 운동 변수를 찾고 이렇게 구한 표적의 운동으로 발생하는 미세도플러를 단일 표적의 미세도플러 영상에서 추출한다[3]. 또한 다표적 환경에서 허프 변환을 이용하는 연구들 중에는 다표적이 존재하는 RP(Range Profile)에서 허프 변환을 이용하여 분리한 RP 데이터를 이용하여 표적별 ISAR영상을 생성하는 연구가 있다[9]. 그리고 노이즈 및 표적의 신호 크기에 영향을 덜 받는 허프 공간에서 다표적을 탐지하는 방법에 대한 연구가 있었다[10].
본 논문에서는 앞에서 언급한 선행연구들과 다르게 다표적 환경에서 표적별 미세도플러 신호를 분리하는 방법에 대해 제안한다. 본 논문에서 제안하는 방법은 다음과 같은 단계를 거친다. 첫 번째 단계에서는 수신한 신호로부터 고해상도 산란점(SC, Scattering Center)을 추출한다. 두 번째 단계에서는 이렇게 추출된 고해상도 산란점을 허프 변환(Hough transform)을 사용하여 표적 이동 궤적별로 분리한다. 세 번째 단계에서는 분리된 산란점들을 사용하여 동적 RCS 신호를 복원하며 이 단계에서 표적이 이동 궤적에 대한 거리 보상이 이루어져 표적의 이동 궤적에 관계없이 균일한 미세 도플러 영상을 얻을 수 있도록 한다. 고해상도 산란점 추출 방법은 노이즈에 비교적 강건하고 동작속도가 빠른 DROP(Dimension Reduced Optimization Problem)을 사용하였다[11]. 이후 추출한 산란점들에 허프 변환을 이용하여 표적별 동적 RCS 신호를 분리하였다. 본 논문의 구성은 다음과 같다. 2장에서는 표적의 분리하는데 사용한 허프 변환에 대해 간단히 설명하였다. 3장에서는 제안하는 허프 변환 기반의 표적 분리 방법을 설명하였다. 4장에서는 알고리즘을 검증하기 위한 시뮬레이션을 수행하고 결과를 제시하였다. 5장에서는 본 논문의 결론을 서술하였다.
Ⅱ. 허프 변환
허프 변환이란 일반적으로 2차원 영상에서 적은 파라미터로 표현할 수 있는 도형을 검출할 수 있는 알고리즘이다. 기존의 레이더 분야에서는 주로 2차원 영상에서 표적들의 경로 검출에 사용되었다. 직선을 검출하기 위한 허프 변환의 수식은 식 (1)과 같다[12].
| (1) |
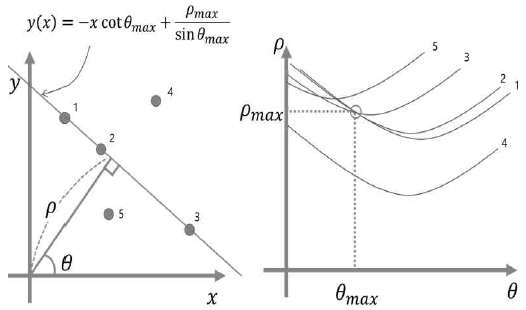
여기서 ρ는 직선이 원점으로부터 떨어져 있는 거리를 나타내며, θ는 ρ와 x축의 사이각이다. 이를 활용하면, θ와 ρ만으로 직선을 표현할 수 있다. θ와 ρ는 그림 1과 같이 표현된다.
2차원 영상에서 픽셀의 좌표가 (x, y)일 때 해당 픽셀좌표로부터 식 (1)에 모든 θ를 대입하여 구한 (θ, ρ)들을 p×q의 크기를 갖는 허프공간에 누적한다. 여기서 θ의 범위는 모든 직선의 기울기를 표현할 수 있도록 0°~ 180°으로 설정한다[7]. 영상의 모든 픽셀을 이용하여, 허프공간에 이산화된 다수의 곡선을 누적시킨다.
허프공간에서 가장 많이 누적된 위치의 ρ와 θ를 ρmax와 θmax라고 하며, 해당 값을 식 (2)에 대입하여 직선을 그리면 그림 1처럼 직선을 얻을 수 있다[12].
| (2) |
Ⅲ. 제안하는 방법
본 논문에서 제안하는 방법은 4가지 가정을 기반으로 한다. 첫 번째 가정은 단일 레이더 빔 내에 다수의 소형 표적이 존재하며, 이 소형 표적들은 표적의 종류별로 서로 다른 미세 거동을 갖는다는 것이다. 두 번째 가정은 레이더가 표적을 매우 짧은 시간 관측하기 때문에 표적의 이동 궤적이 직선으로 근사된다는 것이다. 세 번째 가정은 표적의 크기에 비해 레이더의 대역폭이 작아서 RP에서 표적이 하나의 산란점으로 표현된다는 것이다. 마지막 가정은 자세제어를 수행하는 기두부는 코닝 운동을, 별도의 자세제어를 하지 않는 기만체는 텀블링 운동을 한다는 것이다. 레이더의 수신 신호 는 L×N의 크기를 갖는 복소수 행렬이며, 식 (3)과 같이 표현 할 수 있다.
| (3) |
여기서 En(fl)은 l번째 주파수 샘플 인덱스와 n번째 시간 샘플에 대한 레이더 수신 신호이고, N과 L은 각각 시간과 주파수 샘플 개수를 의미한다. 의 주파수 방향으로 IFFT를 수행하여 RP인 를 얻을 수 있으며, 이는 식 (4)와 같이 표현할 수 있다.
| (4) |
로부터 고해상도 산란점 추출 기법인 DROP 알고리즘을 사용하여 표적의 개수만큼 산란점을 추출한다[6]. 고해상도 산란점 추출 기법을 사용함으로써 산란점의 진폭, 거리, 위상값을 모두 추출할 수 있다. 추출된 산란점들은 표적에 따른 분류가 이루어져 있지 않다. 이러한 산란점들을 표적별로 분류하기 위하여 산란점이 이루는 표적의 궤적을 구하고 해당 궤적에 가장 가까이 있는 산란점을 선택하는 방법을 사용하였다. 추출된 산란점이 이루는 표적의 궤적은 식 (2)와 같이 직선의 방정식으로 표현할 수 있다. 여기서 θmax와 ρmax는 허프 변환을 이용하여 수 있다[12]. 이와 같이 구해진 궤적에 가장 가까운 산란점은 아래의 식 (5)를 이용하여 선택한다.
| (5) |
여기서 y(t)는 시간 t에서 허프 변환으로 구한 궤적의 거리이고, R(k,t)는 시간 t에서 k번째로 추출된 산란점의 거리이다. 이러한 과정을 표적의 개수만큼 반복한다. 추출된 단일 표적에 대한 산란점들을 식 (6)에 대입하면 단일 표적에 대한 동적 RCS를 복원할 수 있다.
| (6) |
여기서 A(k,t)와 θ(k,t)는 시간 t에 k번째로 추출된 산란점의 진폭과 위상이다. 이와 같이 복원된 동적 RCS는 표적의 미세거동성분 뿐만 아니라 표적의 이동에 의한 성분도 포함한다. 표적의 이동속도에 무관한 미세도플러 영상을 얻기 위해서는 추출한 동적 RCS 신호에 거리 보상을 해 주어야 한다. 거리보상을 위해서는 우선 표적의 이동 궤적을 구하여야 한다. 표적의 이동 궤적은 식 (7)과 같이 최소제곱법을 적용함으로써 구할 수 있다[13].
| (7) |
여기서 이고, 이며, 표적의 궤적은 식 (8)과 같이 구할 수 있다.
| (8) |
이와 같이 계산한 표적의 이동 궤적을 식 (9)에 대입하여 표적의 이동에 의한 성분이 제거된 동적 RCS를 얻을 수 있다.
| (9) |
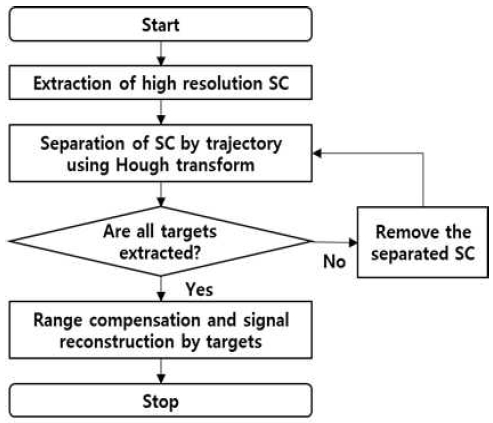
이상의 과정을 거쳐 한 표적에 대한 동적 RCS를 추출한다. 이후 전체 산란점 그룹에서 추출한 표적에 대한 산란점들을 제거한 뒤 나머지 산란점 그룹에 대해서 동일한 과정을 반복하는 방법으로 나머지 표적들에 대한 동적 RCS 신호도 추출할 수 있다. 그림 2는 제안한 방법의 전체적인 순서도이다.
Ⅳ. 시뮬레이션
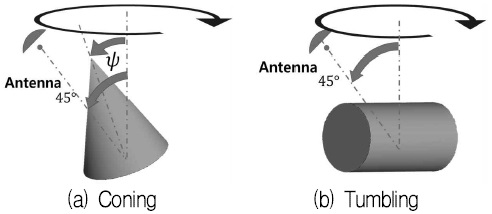
본 논문에서 제안한 방법을 검증하기 위하여 3개의 기두부와 3개의 기만체가 함께 관측되는 상황을 가정하고 시뮬레이션을 수행하였다. 기두부는 원뿔 형상을 가지고 있으며 기만체는 원기둥 형태로 가정하였다. 기두부와 기만체의 3D CAD 모델은 그림 3과 같다. 또한 기두부는 코닝 운동을 기만체는 텀블링 운동을 한다고 가정하였다[4]. 실제 전자파 수치해석 S/W에서 표적별 미세거동을 구현하기 어렵기 때문에 표적의 미세거동에 따른 안테나의 관측각을 계산하였다. 즉, 표적이 정지한 상태에서 미세거동의 회전방향의 역방향으로 레이더의 관측각의 변화를 준다면 표적이 미세거동을 하는 것과 같은 결과를 얻을 수 있게 된다.
그림 4는 이러한 코닝 운동과 텀블링 운동을 전자파 수치해석 S/W에서 표현하는 방법을 보여준다. 이때 코닝 미세운동을 표현하기 위해서 그림 4 (a)와 같이 운동방향에 대해 원뿔의 축을 ψ만큼 기울였다[4]. 표적의 RCS를 계산하기 위해서 상용 전자파 수치해석 S/W인 FEKO[4]를 사용하였으며, 해석 방법은 PO(Physical optics) 기법[14]을 이용하였다.
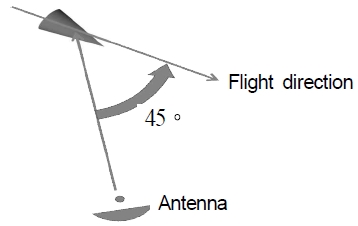
레이더가 표적을 바라보는 LOS(Line of Sight)의 각도는 45°로 가정하였으며 그림 5는 레이더가 표적을 바라보는 각도를 그림으로 표현한 것이다.
시뮬레이션에 사용한 레이더의 시간 및 주파수 관련 매개변수는 표 1과 같으며 표적의 형상과 이동 및 미세거동에 대한 매개변수는 표 2에 정리되어 있다.
그림 6은 참고문헌 [15]를 참조하여 노이즈를 생성한 후, SNR 10dB 환경에서 DROP을 사용하여 로부터 추출한 산란점의 이동 궤적을 보여준다. 산란점의 궤적이 교차하는 지점에서 산란점이 정상적으로 추출되지 않음을 확인할 수 있으나 이러한 부분을 제외한 나머지 부분에서는 산란점이 정확하게 추출되었음을 확인할 수 있다.
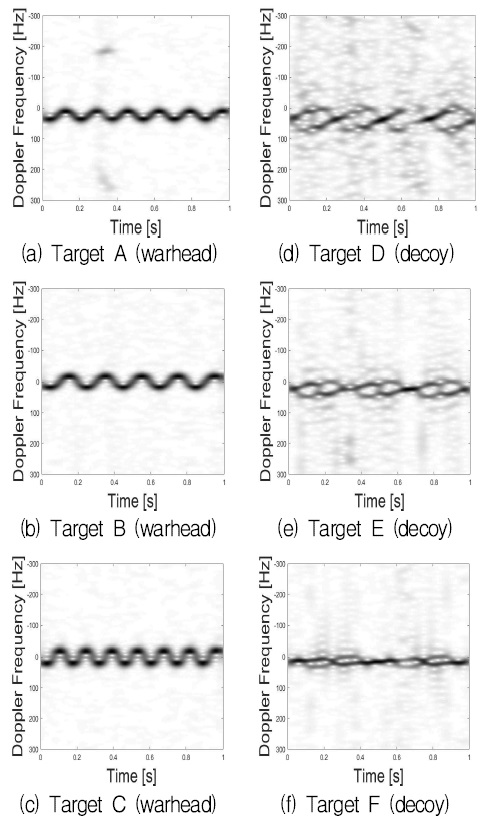
그림 7은 제안된 방법을 사용해서 추출한 동적 RCS에 STFT(Short time Fourier transform)을 적용하여 얻은 각 표적의 미세도플러 영상이다. 대부분의 표적은 미세도플러 영상이 0Hz를 기준으로 진동하고 있으나 일부 영상은 도플러 영상이 도플러 주파수 축 방향으로 시프트 되어 있다. 이러한 문제는 정상적으로 추출되지 않은 산란점들이 거리 보상을 위한 최소제곱법의 결과에 오류를 주어 나타난 결과이다. 이러한 문제점은 Least median square[16]와 같은 산란점에 강건한 최소제곱법을 이용하거나 정상적으로 추출되지 않은 산란점에 대해서는 내삽 기법을 이용하여 다시 계산하는 등의 다양한 방법으로 개선될 수 있을 것이다.
Ⅴ. 결 론
본 논문에서는 하나의 레이더 빔 안에 다수의 미세거동 표적이 있는 상황을 가정하고 각 표적의 미세도플러 성분을 분리할 수 있는 새로운 방법을 제안하였다. 본 논문에서 제안한 방법을 검증하기 위하여 코닝과 텀블링 운동을 하는 6개의 표적에 대하여 SNR 10dB 환경에서 시뮬레이션을 수행하였으며 알고리즘이 성공적으로 동작함을 확인하였다. 본 논문은 다표적 환경에서 표적별 신호 분리에 대한 연구를 수행하였으며 향후에는 본 논문의 연구 결과를 바탕으로 특성 벡터 추출 및 표적 구분에 대한 연구를 수행할 것이다. 또한 산란점 추출 기법으로 DROP 알고리즘을 이용하였으나, 이외에도 다양한 산란점 추출 기법들이 있으므로 이에 대한 성능 분석이 추가적으로 수행되어야 하며 산란점 추출에 실패하였을 경우의 해결 방법에 대해서도 추가 연구가 수행되어야 할 것이다.
Acknowledgments
본 연구는 국방과학연구소의 지원(계약번호:UD170019FD)을 받아 수행하였으며, 이에 감사드립니다.
References
-
S. H. Park, J. S. Yun, and C. K. Ryoo, "Ballistic Missile Tracking using Unscented Kalman Filter", Journal of Institute of Control, Robotics and Systems, Vol. 14, No. 9, pp. 898-903, Sep. 2008.
[https://doi.org/10.5302/J.ICROS.2008.14.9.898]

-
F. Daum and R. Fitzgerald, "Decoupled Kalman filters for phased array radar tracking", IEEE Transactions on Automatic Control, Vol. 28, No. 3, pp. 269-283, Mar. 1983.
[https://doi.org/10.1109/TAC.1983.1103242]

-
I. O. Choi, S. H. Kim, J. H. Jung, K. T. Kim, and S. H. Park, "An Efficient Method to Extract the Micro-Motion Parameter of the Missile Using the Time-Frequency Image", The Journal of Korean Institute of Electromagnetic Engineering and Science, Vol. 27, No. 6, pp. 557-565, Jul. 2016.
[https://doi.org/10.5515/KJKIEES.2016.27.6.557]

- Y. J. Choi, I. S. Choi, J. Shin, and M. Chung, "Classification of the Front Body of a Missile and Debris in Boosting Part Separation Phase Using Periodic and Statistical Properties of Dynamic RCS", The Journal of Korean Institute of Electromagnetic Engineering and Science, Vol. 29, No. 7, pp. 540-549, Jul. 2018.
-
S. H. Seol and I. S. Choi, "Classification of Warhead and Debris using CFAR and Convolutional Neural Networks", The Journal of Korean Institute of Information Technology, Vol. 17, No. 6, pp. 85-94, Jun. 2019.
[https://doi.org/10.14801/jkiit.2019.17.6.85]

-
A. Hyvärinen and E. Oja, "Independent component analysis: algorithms and applications", Neural Networks, Vol. 13, No. 4-5, pp. 411-430, Jun. 2000.
[https://doi.org/10.1016/S0893-6080(00)00026-5]

-
D. P. Rini, S. M. Shamsuddin, and S. S. Yuhaniz, "Particle Swarm Optimization: Technique, System and Challenges", International Journal of Applied Information Systems, Vol. 14, No. 1, pp. 19-27, Jan. 2011.
[https://doi.org/10.5120/1810-2331]

- Yinan Yang, Jiajin Lei, Wenxue Zhang, and Chao Lu, "Target Classification and Pattern Recognition Using Micro-Doppler Radar Signatures", in Seventh ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD’06), Las Vegas, NV, USA, pp. 213-217, Jun. 2006.
-
S. H. Park, K. K. Park, J. H. Jung, H. T. Kim, and K. T. Kim, "ISAR Imaging of Multiple Targets Using Edge Detection and Hough Transform", Journal of Electromagnetic Waves and Applications, Vol. 22, No. 2-3, pp. 365-373, Jan. 2008.
[https://doi.org/10.1163/156939308784160622]

-
B. D. Carlson, E. D. Evans, and S. L. Wilson, "Search radar detection and track with the Hough transform. III. Detection performance with binary integration", IEEE Transactions on Aerospace and Electronic Systems, Vol. 30, No. 1, pp. 116-125, Jan. 1994.
[https://doi.org/10.1109/7.250412]

-
Y. J. Choi and I. S. Choi, "DROP Algorithm for Super Resolution Scattering Center Extraction", Progress In Electromagnetics Research, Vol. 163, pp. 119-132, Nov. 2018.
[https://doi.org/10.2528/PIER18082304]

-
B. D. Carlson, E. D. Evans, and S. L. Wilson, "Search radar detection and track with the Hough transform. I. system concept", IEEE Transactions on Aerospace and Electronic Systems, Vol. 30, No. 1, pp. 102-108, Jan. 1994.
[https://doi.org/10.1109/7.250410]

-
P. Geladi and B. R. Kowalski, "Partial least-squares regression: a tutorial", Analytica Chimica Acta, Vol. 185, pp. 1-17, 1986.
[https://doi.org/10.1016/0003-2670(86)80028-9]

-
H. Shin, S. Lee, D. Park, J. Shin, M. Chung, S. Park, and Y. B. Park, "Analysis of Radar Cross Section of a Battleship Equipped with an Integrated Mast Module Based on PO and PTD", Journal of Electromagnetic Engineering and Science, Vol. 17, No. 4, pp. 238-240, Oct. 2017.
[https://doi.org/10.26866/jees.2017.17.4.238]

- I. S. Choi, "Extraction of Scattering center and Natural Frequency using Evolutionary Programming –based CLEAN", Ph.D. Thesis, POSTECH, 2003.
-
P. J. Rousseeuw, "Least Median of Squares Regression", Journal of the American Statistical Association, Vol. 79, No. 388, pp. 871-880, Dec. 1984.
[https://doi.org/10.1080/01621459.1984.10477105]


2018년 2월 : 한남대학교 전자공학과(공학사)
2019년 3월 ~ 현재 : 한남대학교 전자공학과 공학과정
관심분야 : 레이더 신호처리, 표적인식

2013년 2월 : 한남대학교 전자공학과(공학사)
2018년 2월 : 한남대학교 전자공학과(공학석사)
2018년 3월 ~ 현재 : 한남대학교 전자공학과 박사과정
관심분야 : 레이더 신호처리, RCS 해석 및 분석

1998년 2월 : 경북대학교 전자공학과(공학사)
2000년 2월 : POSTECH 전자전기공학과(공학석사)
2003년 2월 : POSTECH 전자전기공학과(공학박사)
2003년 ~ 2004년 : LG전자 선임연구원
2004년 ~ 2007년 : 국방과학연구소 선임연구원
2007년 ~ 현재 : 한남대학교 전기전자공학과 교수
관심분야 : 레이더 신호처리, 레이더 시스템 설계, RCS 해석 및 분석