경쟁회피 고정 우선순위 스케줄링 알고리즘을 위한 반응 시간 분석기법 연구
초록
경쟁회피(Contention-free) 정책은 멀티프로세서의 특성을 효과적으로 활용한 기법으로서, 기존의 대부분의 실시간 스케줄링 알고리즘에 적용 가능한 기법이다. 이러한 이점에 따라 EDF(Earliest-Deadline First)와 RM(Rate Monotonic)과 같은 특정 스케줄링 알고리즘뿐만 아니라, 고정 우선순위(Fixed priority) 스케줄링 알고리즘에도 적용되었으며, 이를 지원하는 실시간성 분석기법인 마감 시간 분석기법(Deadline analysis)도 개발되었다. 반응 시간 분석기법(Response-time analysis)은 마감 시간 분석기법보다 훨씬 좋은 성능을 보이는 실시간성 분석기법이지만, 경쟁회피 정책이 적용된 EDF와 RM을 대상으로 개발되었고, 고정 우선순위 스케줄링 알고리즘을 위해서는 개발되지 않았다. 본 논문에서는 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘을 지원하기 위한 반응 시간 분석기법을 개발하고, 자체 개발한 시뮬레이터를 통해 그 성능을 분석한다.
Abstract
The CF(contention-free) policy is a technique to effectively utilize the computing power of multi-processor, which can be incorporated into the most existing real-time scheduling algorithms. Utilizing such the advantage, the CF policy was incorporated into EDF(Earliest-Deadline First) and RM(Rate Monotonic) as well as FP(Fixed-Priority) scheduling algorithms, and DA(Deadline Analysis) as schedulability analysis to support them was also developed. Although RTA(Response-Time Analysis) is better-performing schedulability analysis than DA, it was developed for the CF policy incorporated EDF and RM, not for CF policy incorporated FP. In this paper, we propose RTA for the CF policy incorporated FP scheduling algorithm, and evaluate its performance via self-developed simulator.
Keywords:
real-time system, fixed-priority scheduling, contention-free policyⅠ. 서 론
시스템의 정확성이 기능적 측면뿐 아니라 시간적 측면에 의해서도 결정되는 시스템을 실시간 시스템이라고 한다[1][2]. 예를 들어 자동차 시스템에서, 차량을 정확하게 제어하기 위해서는 자동차 휠 제어 시스템이 사전에 정의된 시간 내(즉, 마감 시간)에 오류 없이 정확하게 실행되어야 한다. 실시간 스케줄링은 이러한 시스템을 설계하는 것을 돕는 주요 기법으로서, 시스템에서 실행되는 CPU, 메모리와 같은 컴퓨팅 자원을 효율적으로 할당할 수 있는 방법론이다. 실시간 스케줄링 분야의 광범위한 연구 중에서 스케줄링 알고리즘 설계 및 스케줄링 가능성 분석은 가장 중요한 연구 분야이다. 전자는 실시간 작업의 실행 순서를 결정하는 방법론이며, 후자는 해당 시스템이 스케줄링 알고리즘으로 실행될 때, 마감 시간을 충족시킬 수 있는지 수학적으로 분석하는 기법을 말한다.
지난 수십 년간, 멀티프로세서 플랫폼이 실시간 시스템에 효율적으로 활용되었고, 많은 컴퓨팅 연산을 요구하는 작업이 실시간 시스템에서 실행되게 되었다. 이러한 추세에 따라 실시간 스케줄링 이론에 관한 많은 연구가 진행되었다[3]-[7]. 이들은 실행시간 도중 작업의 우선순위를 효과적으로 변경하는 방법을 제시하거나[3], 실용성을 다소 포기하고 이론적으로 최적의 알고리즘을 제시하거나[4][5], 서로 다른 스케줄링 알고리즘들의 관계를 규명하는[6][7] 등의 새로운 실시간 스케줄링 알고리즘을 개발하는 데 중점을 두었지만, 일부 연구에서는 기존의 스케줄링 알고리즘에 통합될 수 있는 실행 기법을 제안하였다. 후자의 접근법을 확장하는 것은 기존 스케줄링 알고리즘뿐만 아니라 미래에 개발될 알고리즘의 스케줄링 성능을 잠재적으로 향상할 수 있다는 점에서 매우 중요하다. 후자의 접근법의 성공적인 예로서, 제로 렉서티(Zero-laxity) 정책[8]과 경쟁회피(CF, Contention Free) 정책[9]-[11]이 있다. 제로 렉서티 정책은 하나의 실시간 작업이 실행하는 도중, 더 실행하지 않을 때 반드시 마감 시간 위배가 일어나는 순간, 그 실시간 작업에 가장 높은 실행 우선순위를 부여하여 마감 시간 위배의 가능성을 낮추는 기법이다. 반대로, 경쟁회피 기법은 하나의 실시간 작업이 실행하는 도중, 남은 실행시간에 절대로 마감 시간 위배가 일어나지 않는다는 것이 보장될 때, 가장 낮은 우선순위를 부여하여 나머지 실시간 작업의 실행 가능성을 높여 주는 기법이다.
제로 렉서티 정책과 경쟁회피 정책은 광범위한 적용 가능성 및 기존 스케줄링 알고리즘들에 대한 성능 향상의 이점으로 인해 스케줄링 분야에서는 상당히 많은 연구가 진행되어왔다. 경쟁회피 정책의 경우 이러한 이점에 따라 EDF(Earliest Deadline First)[13]와 RM(Rate Monotonic)[13]과 같은 특정 스케줄링 알고리즘뿐만 아니라, 고정 우선순위(FP, Fixed Priority)[14] 스케줄링 알고리즘에도 적용되었으며, 이를 지원하는 실시간성 분석기법인 마감 시간 분석기법(DA, Deadline Analysis)[10][11]도 개발되었다. 반응 시간 분석기법(RTA, Response Time Analysis)[18][19]은 마감 시간 분석기법보다 훨씬 좋은 성능을 보이는 실시간성 분석기법이지만, 경쟁회피 정책이 적용된 EDF와 RM을 대상으로 개발되었고, 고정 우선순위 스케줄링 알고리즘을 위해서는 개발되지 않았다[18].
본 논문에서는 경쟁회피 기법이 적용된 고정 우선순위 스케줄링 알고리즘을 위한 반응 시간 분석기법을 제안하고, 자체 개발한 자바(Java) 시뮬레이터를 이용하여 그 성능을 분석한다. 2장에서는 본 연구에서 대상으로 하는 시스템 모델과 기본 개념들을 설명한다. 3장에서는 배경 지식으로서 기존에 제안된 경쟁회피 기법이 적용된 고정 우선순위 스케줄링의 동작을 소개하며, 4장에서는 이를 지원하는 본 논문에서 제안하는 실시간성 분석기법인 반응 시간 분석기법을 제안한다. 5장에서는 자체개발한 자바 시뮬레이터를 통해 여러 상황에서의 반응 시간 분석기법의 성능을 분석하며, 6장에서는 결론을 맺는다.
Ⅱ. 시스템 모델
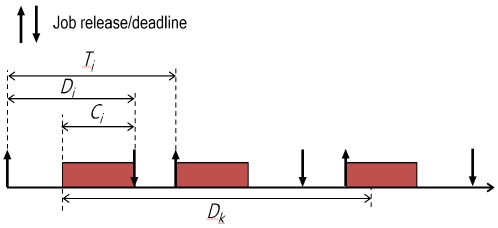
논문에서는 기존의 많은 논문에서 채택하고 있는 Liu & Layland 태스크 모델[13]을 고려한다. 해당 모델에 따라, 태스크(Task)들은 무한히 많은 작업(Job)들을 주기적으로 생성하며, 태스크들의 집합은 τ로 나타낸다. 각각의 태스크 τi는 (Ti, Ci, Di)로 표현되는데, 여기서 Ti는 작업들이 생성되는 주기, Ci는 하나의 작업의 최대 실행시간(Worst-case execution time), Di는 하나의 작업의 생성시간과 마감 시간의 간격을 의미한다. 본 논문에서는 멀티프로세서 환경을 가정한다. 하나의 시간 슬롯은 작업이 실행할 수 있는 최소한의 시간 단위를 의미하여, 하나의 작업은 하나의 시간 슬롯에서 하나의 프로세서에서만 동작한다. 스케줄링 알고리즘으로는 고정 우선순위 스케줄링 알고리즘(Fixed priority scheduling algorithm)을 가정한다. 고정 우선순위 스케줄링 알고리즘은 태스크 자체에 우선순위를 부여하는 스케줄링 기법으로서, 하나의 태스크가 생성하는 모든 작업들은 같은 실행 우선순위를 가지며, 높은 우선순위의 태스크가 생성하는 모든 작업들은 낮은 우선순위의 태스크가 생성하는 모든 작업들보다 높은 우선순위를 가진다. 무경쟁 시간 슬롯은 현재 실행 가능한 작업들의 개수보다 프로세서의 개수(m)가 더 많은 시간 슬롯을 의미한다. 따라서, 무경쟁 시간 슬롯에서는 모든 작업들이 경쟁 없이 실행할 수 있음이 보장된다.
Ⅲ. 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘
본 장에서는 배경 지식으로서 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘과 무경쟁 시간 슬롯의 계산 방법에 관해 설명한다.
3.1 알고리즘
먼저 고정 우선순위의 스케줄링 패턴과 경쟁회피 정책이 적용된 고정 우선순위 스케줄링의 패턴에 관해 설명한다.
그림 1(a)는 세 개의 태스크 τ1(15, 4, 9), τ2(15, 4, 9), τ3(15, 7, 10)가 두 개의 프로세서를 가지는 시스템에서 고정 우선순위 스케줄링 알고리즘에 의해 실행될 때의 스케줄링 패턴을 나타내며, 그림 1(b)는 해당 스케줄링 알고리즘에 경쟁회피 정책이 적용되었을 때의 스케줄링 패턴을 나타낸다. 고정 우선순위 스케줄링 알고리즘으로 태스크에 우선순위를 할당하는 방법은 무수히 많이 있으며, 본 예제에서는 τ1가 가장 높은 우선순위를 τ2가 중간 우선순위를 τ3가 가장 낮은 우선순위를 가진다고 가정한다.
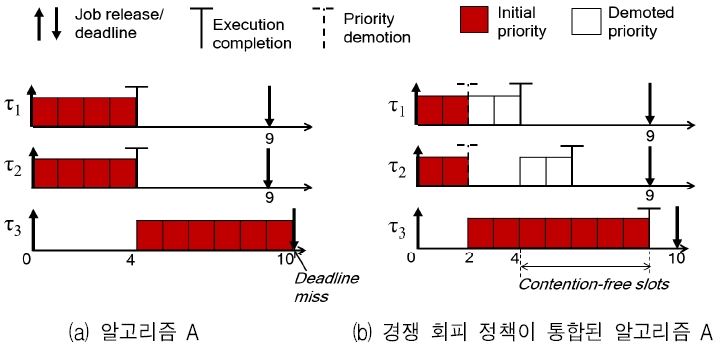
Example of fixed-priority scheduling and that with contention-free policy, (a) Algorithm A, (b) Algorithm A with integrated competition avoidance policy
그림 1(a)에서 볼 수 있듯이 0부터 4 사이의 시간 슬롯에서 τ1와 τ2의 작업들이 각각의 프로세서에서 실행이 되며, 이 둘의 실행이 끝난 후 τ3의 작업이 실행을 시작하게 된다. 하지만 τ3의 작업이 실행 끝마치는 데 필요한 시간 슬롯은 7인 반면, 남은 시간 슬롯은 6이므로 10의 시간에서 마감 시간을 위배하게 된다.
그림 1(b)는 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘으로 인해 모든 태스크가 마감 시간 위배 없이 실행 가능해지는 시나리오를 나타낸다.
경쟁회피 정책은 먼저 각각의 태스크의 작업들의 생성시간과 마감 시간 내에 존재하는 최소한의 무경쟁 시간 슬롯의 개수를 계산하게 된다. (3.2장에서 무경쟁 시간 슬롯의 개수를 계산하는 기법을 설명한다) 이 계산 때문에 τ1와 τ2의 접들의 생성시간과 마감 시간 사이에 최소 두 개의 무경쟁 시간 슬롯이 존재하게 된다. 0과 4 사이의 시간 슬롯에서는 실행 가능한 접의 수가 3이고 프로세서의 개수가 2이므로 세 개의 접들은 프로세서를 이용하기 위해 경쟁해야 하는 경쟁시간 슬롯이다. 경쟁회피 정책에 의해 시간 2에서 τ1와 τ2의 작업들이 최하위 실행 우선순위가 되어 τ1의 작업이 시간 2부터 실행을 하게 된다.
그 이유는 계산 때문에 τ1와 τ2의 작업들은 최소 두 개의 무경쟁 시간 슬롯을 가지게 되며, 0부터 2 사이에 무경쟁 시간 슬롯이 존재하지 않는다는 뜻은 나머지 실행은 무경쟁 시간 슬롯에서 실행 가능하며 마감 시간 위배가 절대 일어날 수 없는 것을 뜻하기 때문이다. 이렇듯, 남아 있는 실행시간과 남아 있는 무경쟁 시간 슬롯의 비교를 통해 우선순위를 동적으로 하강시켜 멀티프로세서의 계산력을 효율적으로 사용할 수 있다.
그림 1(a)에서는 볼 수 있듯이 두 프로세서가 모두 사용되는 시간이 4에 그치지만, 그림 1(b)에서 볼 수 있듯이 경쟁회피 정책이 적용된 경우 두 프로세스가 모두 사용되는 시간이 6으로 늘어남을 알 수 있다.
그림 2는 경쟁회피 정책이 적용된 고정 우선순위 스케줄링의 동작을 나타낸다. 각각의 시간 슬롯에 대해 하나의 태스크 τi가 하나의 작업을 생성할 때, 이 작업을 QH에 넣는다. 그리고 해당 작업에 해당하는 무경쟁 시간 슬롯(Φi)의 개수를 구하고, 잔여 실행시간 Ci(t)과 잔여 무경쟁 시간 슬롯(Φi(t))의 개수를 각각 Ci와 Φi로 초기화시킨다(라인 1~3).
만약 해당 시간 슬롯에서 잔여 실행시간 Ci(t)이 ΦiN(t)보다 작거나 같은 작업이 존재한다면 해당 작업을 QL로 이동시킨다(라인 4~8). QH에 존재하는 각각의 작업들에 대해 현재시간 슬롯이 무경쟁 시간 슬롯이면 Φi(t)을 1만큼 감소시킨다(라인 9-10). QH에 존재하는 작업들을 고려하는 고정 우선순위 알고리즘으로 우선순위를 할당한다(라인 11). 마지막으로 m의 작업을 실행한다. 여기서 QH에 존재하는 모든 작업들은 QL에 존재하는 모든 작업들보다 높은 우선순위를 가진다.
3.2 무경쟁 시간 슬롯 계산
그림 2에서 살펴본 바와 같이 경쟁회피 정책은 먼저 각각의 태스크에 대해 해당 작업의 마감 시간 전에 존재할 수 있는 무경쟁 슬롯의 최소 개수를 구하게 되며(라인 2), 작업이 실행하는 도중 남은 실행시간과 남은 무경쟁 슬롯의 개수가 같아지면 그 작업의 실행 우선순위를 최하위로 하강시킨다(즉, QL로 이동시킨다). 우선순위가 하강 된 작업은 적어도 남은 실행량만큼의 무경쟁 슬롯을 만날 수 있으므로 마감 시간 위배가 절대 일어날 수 없게 된다. 이번 장에서는 각각의 태스크에 대해 무경쟁 시간 슬롯을 계산하는 방법에 대해 알아본다.
경쟁회피 정책이 적용된 실시간 스케줄링 하에서는 각각의 태스크에 대해 무경쟁 시간 슬롯의 개수를 실행 이전에 미리 계산하게 되며, 실행 동안 무경쟁 슬롯을 만날 때마다 그 값이 감소하게 된다. 무경쟁 시간 슬롯의 계산에 있어서 사용되는 기본적인 개념은 하나의 작업의 생성시간과 마감 시간 사이에 존재할 수 있는 모든 작업들의 실행 로드들을 먼저 분석한다.
그 후 작업들이 프로세서의 사용을 위해 경쟁해야 하는 (즉, 실행이 가능한 작업들의 개수보다 프로세서 개수가 작은) 시간 슬롯의 최댓값을 구한다. 이 값을 경쟁시간 슬롯값이라고 하는데, 이 값을 이용하여 존재하는 시간 슬롯에서 경쟁시간 슬롯값을 제외하면 최소한의 무경쟁 시간을 계산할 수 있게 된다.
τk가 생성하는 작업의 생성시간과 마감 시간 사이(즉, Dk구간)에 존재할 수 있는 최소한 무경쟁 시간 슬롯의 개수를 구하기 위해 먼저 Dk구간 내에 존재할 수 있는 최대한의 실행량을 먼저 구해야 한다.
그림 3은 Dk구간 내에서 존재할 수 있는 τi의 최대 실행 가능량을 나타낸다[15]. 그림 3에서 볼 수 있듯이 τi의 최대 실행이 발생하는 시나리오에서는 첫 번째 작업의 실행 시작이 Dk구간의 시작부터 이루어지며, 종료가 해당 작업의 마감 시간에서 이루어진다. 그다음의 작업들은 생성되자마자 실행되어 최대한 많은 양의 실행이 이루어지게 된다. Dk구간 내에서 존재할 수 있는 τi의 최대 실행량은 Ck만큼 실행 가능한 작업들의 개수와 그렇지 않은 작업의 실행량의 합으로 계산되어 진다. 그림 3에서 유추할 수 있듯이 Dk구간 안에서 Ci만큼 실행하는 태스크 τi가 생성한 작업들의 개수는 다음과 같이 계산된다.
| (1) |
그림 3을 예로 들면, 식 (1)에 의해 계산된 값은 2가 되며, 가장 왼쪽의 작업과 중간의 작업이 Ci만큼 실행할 수 있다. 다음으로, Ci만큼 실행하지 못하는 작업(그림 3의 가장 오른쪽 작업)의 최대 실행 로드는 min(Ci,Dk+Di-Ci-ni(Dk•Ti))이다. 이 값과 식 (1)을 이용하여 Dk구간에서의 τi의 최대 실행 로드 Wi(Dk)는 다음과 같이 계산된다.
| (2) |
Dk구간에서 존재할 수 있는 최대 실행 로드인 Wi(Dk)를 이용하여 Dk구간에 존재할 수 있는 최소 무경쟁 시간 슬롯의 개수를 구한다. m개의 프로세서를 가정하므로 Dk구간에 존재할 수 있는 실행 가능한 시간 공간의 크기는 m•Dk이다. 하나의 경쟁시간 슬롯에서는 적어도 m의 작업들이 실행을 하게 된다. 따라서 Dk구간에서 존재할 수 있는 경쟁시간 슬롯의 개수는 아래의 값을 넘지 못한다.
| (3) |
식 (3)에서 구해진 Dk구간에 존재하는 최대 경쟁 시간 슬롯값을 이용하여 아래와 같이 Dk구간에 존재하는 최소한의 무경쟁 시간 슬롯값을 구할 수 있다.
| (4) |
Dk구간에서 τk의 작업은 반드시 하나만 생성되므로, 식 (4)에서 τk의 최대 실행 값은 Wk(Dk)가 아니라 Ck이다.
Ⅳ. 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘을 위한 반응 시간 분석기법
본 장에서는 먼저 일반적인 고정 우선순위 스케줄링에서의 반응 시간 분석기법을 소개하고 이를 경쟁회피 정책이 적용된 고정 우선순위 스케줄링으로 확장한다.
하나의 작업이 생성된 이후 실행시간을 완료할 때까지 걸리는 시간을 반응 시간이라고 한다. 반응 시간 분석기법은 각각의 태스크 τk마다 생성될 수 있는 작업들의 반응 시간을 구하고 이 값이 Dk보다 작으면 모든 작업이 마감 시간 내에 실행을 끝마칠 수 있는 것으로 판단한다. τk이 생성한 하나의 작업의 생성시간을 시작으로 하는 어떠한 구간 L이 있다고 가정하자. 구간 L안에서 τk가 생성한 작업이 실행을 끝마칠 수 있다면 우리는 L이 τk의 반응 시간의 상계(Upper bound)라고 할 수 있다. m개의 프로세서를 가지는 시스템에서 하나의 작업이 하나의 시간 슬롯에서 실행을 방해받기 위해서는 높은 우선순위를 가지는 m개의 작업이 필요하다. Wi(L)은 L 구간에서 존재하는 τi의 최대 실행량이므로 아래의 식을 만족하면 τk의 작업은 L(Ck≤L≤Dk) 구간에서 실행을 끝마칠 수 있게 된다.
| (5) |
Wi(L)이 Ck보다 크면 τk의 작업과 동시에 실행하게 되므로 L-Ck+1로 바운드하였다. 하나의 태스크 τk에 대해 식 (5)를 만족하는 L은 여러 개 존재할 수도 있고, 존재하지 않을 수도 있다. 반응 시간 분석기법은 최대한 작은 L을 찾기 위해 다음과 같은 절차를 이용한다. 먼저 L을 Ck로 세팅하고 식 (5)를 만족하는지 확인한다. 그렇지 않으면 L을 식 (5)의 부등호 왼쪽 값으로 세팅한다. 그리고 다시 식 (5)를 만족하는지 확인한다.
이러한 절차를 반복적으로 수행하는 동안 Ck≤L≤Dk를 만족하는 L을 찾게 된다면, τk는 L안에서 실행을 끝마칠 수 있다는 것을 의미하고, L이 증가하여 Dk를 넘어가게 되면 Dk구간 안에서 실행을 끝마칠 수 없다고 판단하여, 마감 시간 위배를 의미하게 된다.
다음으로 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘을 위한 반응 시간 분석기법을 구한다.
그림 4는 경쟁회피 정책이 적용되었을 때의 Dk구간에서 존재할 수 있는 τi의 최대 실행량을 나타낸다. τi의 작업이 실행을 하는 동안 최소 Φi만큼의 무경쟁 시간 슬롯이 존재한다. 이것은 τk의 작업도 그 시간 슬롯에서는 τi의 작업에 의해 방해를 받지 않고 실행할 수 있다는 뜻이므로 τi의 각 작업에 대해 Φi만큼은 방해 시간의 계산에서 제외할 수 있다. 따라서, 경쟁회피 정책이 적용된 고정 우선순위 스케줄링 알고리즘에서의 Dk구간에서의 τi의 최대 실행 로드 는 다음과 같이 계산된다.
| (6) |
| (7) |
이 식을 이용하여 아래의 식을 만족하면 τk의 작업은 L(Ck≤L≤Dk) 구간에서 실행을 끝마칠 수 있게 된다.
| (8) |
Ⅴ. 실 험
이번 장에서의 본 논문에서 제안한 경쟁회피 스케줄링 기법이 적용된 고정 우선순위 스케줄링을 위한 반응 시간 분석기법의 성능을 검증한다. 실험을 위해 자체 개발한 자바 시뮬레이터를 이용하여 랜덤하게 생성된 태스크 집합 중 고려되는 기법들에 따라 마감 시간 위배가 없음이 보장되는 태스크 집합의 수를 측정한다. 시뮬레이터는 스케줄링 알고리즘과 이를 지원하는 실시간성 분석기법을 각각 구현하고 있다. 스케줄링 알고리즘의 정확도 확인을 위해 시뮬레이터 상의 실행의 매초 마다 예상되는 스케줄링 결과가 도출되는지 일일이 확인하는 과정을 거친다.
실시간성 분석기법의 경우, 실시간성 분석기법이 해당 태스크에서 마감 시간 위배가 없다고 판단되었을 때, 스케줄링 결과에서도 마감 시간 위배가 실제로 없는지 비교를 통해 정확도를 확인한다. 즉, 스케줄링 알고리즘과 실시간성 분석기법의 성능에는 반드시 이러한 필요 관계(반대의 경우 충분 관계)가 성립하여야 하므로 이러한 비교를 통해 해당 스케줄러의 정확도를 판단하게 된다.
태스크의 무작위 생성을 위해 기존에 알려진 태스크 집합 생성기법을 이용한다[15][16]. 해당 기법은 2005년 처음 제안된 이후 수많은 실시간성 분석기법에 관한 연구에서 채용된 사실상의 표준 성능 기법의 하나로 간주 되고 있다.
또한, 해당 기법은 많은 연구에서 무인기와 같은 실제 실시간 시스템의 동작을 충분히 묘사 가능한 것으로 입증되었다. 해당 태스크 집합 생성기법에 따라, 생성 과정에서 두 개의 입력 m∈{2, 4, 8, 16, 32}, 태스크의 프로세서 이용률(Ci/Ti) 분산(입력 인자 p∈{0.1, 0.3, 0.5, 0.7, 0.9}를 갖는 지수분포)를 갖는다. 해당 입력 인자를 이용하여, 각각의 태스크 τi의 Ti는 1과 1000사의 수중 임의의 값으로 결정되며, Ci는 태스크 집합의 입력에 해당하는 지수분포를 따르며, Di는 Ti와 정해진 Ci사이의 값 중 임의의 수로 결정된다. 각 입력 인자에 대해 1,000개의 태스크 집합이 생성되며, 총 5×5×1,000=25,000개의 태스크 집합이 생성된다.
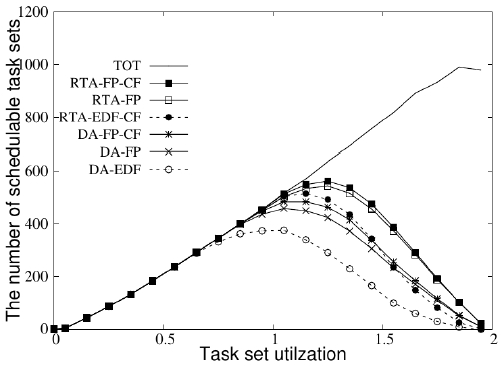
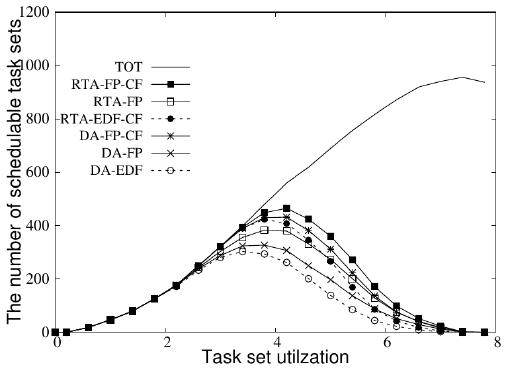
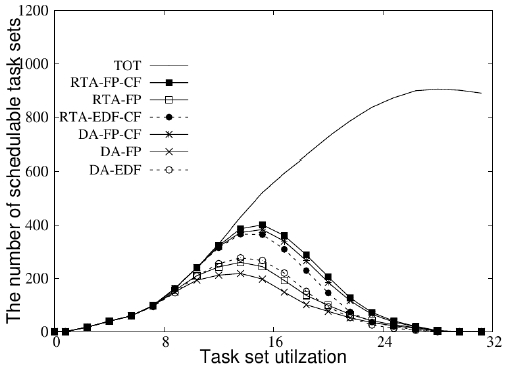
그림 5, 6, 7은 서로 다른 프로세서 개수 (m=2, 8, 32)에 대해 프로세스 이용률 ()의 변화에 각 실시간성 분석기법의 성능이 변화하는 추이를 나타낸다.
본 논문은 기존에 제안된 경쟁회피 기법인 적용된 고정 우선순위 스케줄링 알고리즘에 대한 새로운 실시간성 분석기법을 다루므로, 모든 성능평가의 고려대상은 실시간성 분석기법이다.
해당 그림에서 TOT(Total)는 각 프로세스 이용률에 해당하는 생성된 태스크 집합의 수를 나타내며, RTA-FP –CF는 본 논문에서 제안한 경쟁회피 스케줄링 기법이 적용된 고정 우선순위 스케줄링을 위한 반응 시간 분석기법을 나타낸다.
(1) RTA-FP, (2) RTA-EDF –CF, (3) DA-FP-CF, (4) DA-FP, (5) DA- EDF는 제안한 기법의 비교 대상으로서, (1) 경쟁회피 기법이 적용되지 않은 고정 우선순위 스케줄링을 위한 반응 시간 분석기법, (2) 경쟁회피 기법이 적용된 EDF를 위한 마감 시간 분석기법, (3) 경쟁회피 기법이 적용된 고정 우선순위 스케줄링을 위한 마감 시간 분석기법, (4) 경쟁회피 기법이 적용되지 않은 고정 우선순위 스케줄링을 위한 마감 시간 분석기법, (5) 경쟁회피 기법이 적용되지 않은 EDF를 위한 마감 시간 분석기법을 각각 의미한다.
실험 결과에서 볼 수 있듯이 고려하는 프로세서의 개수가 많아짐에 따라, 모든 실시간 분석기법들의 성능이 저하되는 것을 볼 수 있다. 예를 들어 m이 2일 때, RTA-FP-CF가 최대 552개의 태스크 집합이 마감 시간 없이 실행됨을 보장했던 것과 달리 m이 32일 때, 최대 407개의 태스크 집합에 대해서만 보장해 줌으로써, 407/552≒73.7%의 성능만을 보인다. 이것은 태스크 집합 생성기법의 특성에 따른 것으로 m이 증가함에 따라, 하나의 태스크 집합이 가질 수 있는 태스크의 수가 증가하기 때문이다. 이로 인해, 하나의 태스크가 가질 수 있는 평균적인 높은 우선순위의 태스크 개수가 많아진다.
그림 3에서 다룬 해당 구간 내에서의 최대 실행량은 정확한 값이 아닌 최댓값을 구하기 위한 추정값으로서 실제의 값과 차이가 크게 날 수 있다. 높은 우선순위를 가지는 태스크 개수가 많아질수록 이러한 차이 더욱 누적되게 되며, 하나의 태스크가 겪을 수 있는 방해 시간의 정확도는 더욱 떨어지게 된다. 이러한 현상으로 인해 m이 증가할수록 실시간성 분석기법들의 성능은 떨어진다.
다음으로, 모든 m에 대하여 고정 우선순위 스케줄링 알고리즘을 위한 실시간성 분석기법들을 비교하여 볼 때, RTA-FP-CF가 가장 높은 성능을 보이는 것을 알 수 있다. 예를 들어, m이 2일 때 두 번째로 나은 성능을 보이는 RTA-FP보다 12개가 더 많은 태스크 집합에 대해 마감 시간 위배가 없음을 보장해 주며(552/540≒1.022, 즉, 약 2.2% 성능향상), m이 32일 때는 두 번째로 나은 성능을 보이는 DA-FP-CF보다 10개가 더 많은 태스크 집합에 대해 마감 시간 위배가 없을 보장해 준다(407/397≒1.025, 즉, 약 2.5% 성능향상). RTA-FP와의 비교에 있어, RTA-FP-CF는 각각의 높은 우선순위를 가지는 태스크의 작업들에 대해 실행량을 계산할 때, Φi만큼 제외하기 때문에 RTA-FP보다 더 나은 성능을 보이게 된다. 이러한 RTA-FP와 RTA-FP-CF의 성능 차이는 식 (5)와 식 (8)로부터 비롯된다. RTA-FP-CF는 DA-FP-CF와의 비교에 있어, 역시 항상 높은 성능을 보이는데, 이것은 RTA-FP-CF는 L이 Ck부터 Dk까지 변화하며, 식 (8)을 만족하는 L을 구하지만, DA-FP-CF는 Dk구간에서만 해당 태스크의 작업이 실행을 끝마칠 수 있는지 판단하기 때문이다. DA는 Φi만큼 높은 우선순위의 작업들의 실행이 제외되지도 않고, Dk구간에서만 해당 태스크의 작업이 실행을 끝마칠 수 있는지 판단하기 때문에 항상 RTA-FP-CF, RTA-FP, DA-FP-CF보다 낮은 성능을 보인다.
마지막으로, RTA-FP-CF는 경쟁회피 기법이 적용된 EDF를 지원하는 반응 시간 분석기법인 RTA-EDF-CF와 경쟁회피 기법이 적용되지 않은 EDF를 지원하는 마감 시간 분석기법인 DA-EDF보다 높은 성능을 보임을 알 수 있다. 예를 들어, m이 8일 때 RTA-EDF-CF는 최대 482개의 태스크 집합에 대해 마감 시간 위배가 없음을 보장하는 반면, RTA-EDF-CF는 최대 410개의 태스크 집합에 대해 마감 시간 위배가 없음을 보장한다 (482/410≒1.175, 즉, 약 17.5% 성능향상). 이러한 현상은 다음과 같은 두 가지 이유에서 비롯된다. 첫 번째로 같은 반응 시간 분석기법이 적용되었음에도, 고정 우선순위 스케줄링 알고리즘이 멀티프로세서에서 더욱 잘 동작하기 때문이다[5][6]. 두 번째로 EDF에 의해 스케줄링 되는 태스크의 실시간성을 분석할 때, 해당 태스크를 제외한 모든 태스크를 높은 우선순위를 가지는 태스크로 간주한다. 이것은 EDF의 경우 태스크로부터 생성되는 작업의 우선순위가 매번 달라지기 때문에, 특정한 태스크의 작업들만 높은 우선순위 혹은 낮은 우선순위라고 판단하는 것이 불가능하기 때문이다. 반면, 고정 우선순위 스케줄링 알고리즘은 각각의 작업이 아니라 태스크 자체에 우선순위를 부여하므로 특정 태스크의 입장에서 일부의 태스크는 높은 우선순위로 간주하며, 나머지 태스크는 낮은 우선순위로 간주한다. 따라서 고정 우선순위 스케줄링 알고리즘이 실시간성 분석기법에 대해 훨씬 더 나은 성능을 보이게 된다.
Ⅵ. 결론 및 향후 과제
본 논문에서는 경쟁회피 정책이 적용된 스케줄링에 대한 반응 시간 분석기법이 EDF와 RM과 같은 특정 스케줄링 알고리즘에 대해서만 제안된 점에 착안하여 경쟁회피 정책이 적용된 고정 우선순위 스케줄링에 대한 반응 시간 분석기법을 제안하고 시뮬레이션 실험을 통해 이에 대한 성능을 분석하였다. 성능분석 결과, 본 논문에서 제안한 기법은 기존에 제안된 경쟁회피 정책이 적용된 EDF에 비해 최대 17.5%의 성능향상을 보였다. 경쟁회피 정책이 적용되지 않은 고정 우선순위 스케줄링과 비교하면 최대 2.5%의 성능향상이 있음을 확인하였다. 따라서, 본 논문에서 제안한 분석기법을 이용하면, 고정 우선순위 스케줄링이 적용된 시스템에서의 마감 시간 위배 여부를 분석할 수 있을 뿐만 아니라, 같은 컴퓨팅 자원으로 (예를 들어 m = 2, 8, 32) 더 많은 종류의 시스템을 마감 시간 위배 없이 스케줄링할 수 있음을 확인하였다.
후속 연구로서 반응 시간 분석기법의 성능을 좀 더 개선 시켜 새로운 실시간성 분석기법을 제안하는 방향이 있을 것이다. 또한, 각각의 태스크들이 서로 다른 중요도를 가지는 혼합임계 시스템이나[20], 사이버 물리 시스템으로의 확장도 후속 연구가 될 수 있을 것이다[21].
Acknowledgments
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2019R1F1A1059663).
References
- Y. S. Kim, "Feasibility Study of Real-Time Programs in Linux", Journal of Korea Institute of Information Technology, Vol. 10, No. 8, pp. 127-134, Aug. 2012.
-
J. H. Lee and J. K. Choe, "A Study on Self-localization for Autonomous Mobile Robot", Journal of KIIT, Vol. 11, No. 12, pp. 29-34, Dec. 2013.
[https://doi.org/10.14801/kiitr.2013.11.12.29]

- S. K. Lee, "On-line multiprocessor scheduling algorithms for real-time tasks", Region 10's Ninth Annual International Conference, Singapore, Singapore, IEEE, pp. 607-611, Aug. 1994.
-
S. Baruah, N. K. Cohen, C. G. Plaxton, and D. A. Varvel, "Proportionate progress: a notion of fairness in resource allocation", Algorithmica, Vol. 15, No. 6, pp. 600-625, Jun. 1996.
[https://doi.org/10.1007/BF01940883]

-
J. Y.-T. Leung, "A new algorithm for scheduling periodic, real-time tasks", Algorithmica, Vol. 4, pp. 209-219, Jun. 1989.
[https://doi.org/10.1007/BF01553887]

-
H. S. Chwa, H. Back, S. Chen, J. Lee, A. Easwaran, I. Shin, and I. Lee, "Extending Task-level to Job-level Fixed Priority Assignment and Schedulability Analysis Using Pseudo-deadline", IEEE 33rd Real-Time Systems Symposium, San Juan, Puerto Rico, pp. 51-62, Dec. 2012.
[https://doi.org/10.1109/RTSS.2012.58]

-
H. Baek, H. S. Chwa, and J. Lee, "Beyond Implicit-Deadline Optimality: A Multiprocessor Scheduling Framework for Constrained-Deadline Tasks", IEEE Real-Time Systems Symposium (RTSS), Paris, France, pp. 331-333, Dec. 2017.
[https://doi.org/10.1109/RTSS.2017.00038]

-
T. Baker, M. Cirinei, and M. Bertogna, "EDZL scheduling analysis", 19th Euromicro Conference on Real-Time Systems (ECRTS'07), Pisa, Italy, pp. 9-18, Jul. 2007.
[https://doi.org/10.1109/ECRTS.2007.14]

-
J. Lee, A. Easwaran, and I. Shin, "Maximizing Contention-Free Executions in Multiprocessor Scheduling", Real-Time and Embedded Technology and Applications Symposium, IEEE, Chicago, USA, pp. 235-244, Apr. 2011.
[https://doi.org/10.1109/RTAS.2011.30]

-
J. Lee, A. Easwaran, and I. Shin, "Contention-Free Executions for Real-Time Multiprocessor Scheduling", Transactions on Embedded Computing Systems, ACM, Vol. 13, No. 2s, Article 69, pp. 1-25, Jan. 2014.
[https://doi.org/10.1145/2494530]

-
H. Baek, J. Lee, and I. Shin, "Multi-Level Contention-Free Policy for Real-Time Multiprocessor Scheduling", Journal of Systems and Software, Vol. 137, pp. 36-49, Mar. 2018.
[https://doi.org/10.1016/j.jss.2017.11.027]

-
M. Joseph and P. Pandya, "Finding Response Times in a Real-Time System", The Computer Journal, Vol. 29, No. 5, pp. 390-395, Jan. 1986.
[https://doi.org/10.1093/comjnl/29.5.390]

-
C. Liu and J. Layland, "Scheduling algorithms for multiprogramming in a hard-real-time environment", Journal of the ACM, Vol. 20, No. 1, pp. 46-61, Jan. 1973.
[https://doi.org/10.1145/321738.321743]

- A. Mok, "Fundamental design problems of distributed systems for the hard-real-time environment", Ph.D. thesis, Massachusetts Institute of Technology, May 1983.
-
M. Bertogna, M. Cirinei, and G. Lipari, "Schedulability analysis of global scheduling algorithms on multiprocessor platforms", Transactions on Parallel and Distributed Systems, IEEE, Vol. 20, No. 4, pp. 553-566, Jul. 2009.
[https://doi.org/10.1109/TPDS.2008.129]

- T. P. Baker, "Comparison of empirical success rates of global vs. partitioned fixed-priority EDF scheduling for hard real-time", Technical report, TR–050601, Department of Computer Science, Florida State University, Tallahassee, Aug. 2005.
-
B. Andersson, K. Bletsas, and S. Baruah, "Scheduling arbitrary-deadline sporadic task systems on multiprocessor", Real-Time Systems Symposium, Barcelona, Spain, pp. 385-394, Dec. 2008.
[https://doi.org/10.1109/RTSS.2008.44]

-
H. Baek and J. Lee, "Improved schedulability analysis of the contention-free policy for real-time systems", Journal of Systems and Software, Vol. 154, pp. 112-124, Aug. 2019.
[https://doi.org/10.1016/j.jss.2019.04.067]

-
H. Baek, "Multi-level contention-free policy for rate monotonic scheduling algorithm on real-time systems", Journal of KIIT, Vol. 16, No. 2, pp. 29-38, Feb. 2018.
[https://doi.org/10.14801/jkiit.2018.16.2.29]

-
S. Vestal, "Preemptive scheduling of multi-criticality systems with varying degrees of execution time assurance", Real-Time Systems Symposium, IEEE, Tucson, Arizona, pp. 239-243, Dec. 2007.
[https://doi.org/10.1109/RTSS.2007.47]

-
H. Chwa, K. G. Shin, H. Baek, and J. Lee, "Physical-state-aware dynamic slack management for mixed-criticality systems", Real-Time and Embedded Technology and Applications Symposium, IEEE, Porto, Portugal, pp. 129-139, Apr. 2018.
[https://doi.org/10.1109/RTAS.2018.00023]


2010년 2월 : 건국대학교 컴퓨터공학과(공학사)
2012년 2월 : 한국과학기술원 전산학과(공학석사)
2016년 8월 : 한국과학기술원 전산학과(공학박사)
2018년 5월 : 성균관대학교 박사 후 연구원
2019년 2월 : 국방과학연구소 선임연구원
2019년 3월 ~ 현재 : 인천대학교 컴퓨터공학부 조교수
관심분야 : 실시간 시스템, 사이버 물리 시스템

2012년 2월 : 고려대학교 기계공학과(공학사)
2018년 2월 : 포항공과대학교 창의IT융합공학과(공학박사)
2018년 5월 ~ 현재 : 국방과학연구소 선임연구원
관심분야 : 비선형 제어, 로봇 제어, 인공위성 제어