인공 신경망과 퍼지를 이용한 최대 전력점 추적을 위한 모델
초록
태양광 발전은 일사량 및 온도 등 외부변화에 따른 안정적이고 효율적인 최대 전력 출력 전력점을 추적하기 위한 MPPT 알고리즘이 필요하다. 본 연구는 인공 신경망을 이용하여 기존 MPPT 알고리즘보다 신속하게 MPP를 추적할 수 있는 모델을 구현하였다. 제안 모델은 인공 신경망의 학습 데이터를 위해 다양한 일사량과 온도의 조합에 대해서 기존 MPPT 알고리즘으로 MPP의 전류와 전압을 찾았다. 획득한 MPP 데이터는 입력 노드를 일사량과 온도로 출력 노드를 전류와 전압으로 하여 학습하였다. 실험결과 일사량과 온도 변화가 있는 0~0.3t 구간에서 추적시간은 기존 알고리즘인 P&O와 InC 그리고 Fuzzy는 각각 잘못된 계산식t, 0.49t 그리고 0.4076t이였으며, 제안 모델은 0.32511t로서 기존 알고리즘 보다 0.1t 이상 신속하게 MPP를 추적하였다.
Abstract
Photovoltaic power generation requires MPPT algorithm to track stable and efficient maximum power output power point according to external changes such as solar radiation and temperature. This study implemented a model that could track MPP more quickly than original MPPT algorithm using artificial neural network. The proposed model finds the current and voltage of MPP using the original MPPT algorithm for various combinations of insolation and temperature for training data of artificial neural networks. The acquired MPP data was learned using the input node as insolation and temperature and the output node as the current and voltage. The Experiment results show tracking time of the original algorithms P&O, InC and Fuzzy were respectively 0.428t, 0.49t and 0.4076t for the 0t~0.3t range, and MPP tracking time of the proposed model was 0.32511t and it is 0.1t faster than the original algorithms.
Keywords:
photovoltaic, mppt, neural network, perturbation and observation, incremental conductance, fuzzyⅠ. 서 론
태양광 발전은 태양에너지를 전기에너지로 변환하는 방식으로 일사량만 있으면 어디서나 전기에너지를 얻을 수 있기 때문에 다른 발전방식과 달리 소음, 진동 등의 2차 공해가 없는 에너지원으로 각광받고 있다. 그러나 초기 투자비와 발전단가가 높고, 설치장소가 한정적이며, 에너지 밀도가 낮아 큰 설치면적이 필요하다. 또한, 일사량 및 온도 등 외부 변화에 따라 전압과 전류가 바뀌는 불안정한 전력 공급 장치로서 기존의 발전방식들과 비교해서 안정적인 전력을 출력하기가 기술적으로 쉽지 않다. 따라서 태양광 발전 시스템은 외부변화에 대해서 안정적이고 효율적인 최대 전력점(MPP, Maximum Power Point)을 추적하기 위한 최대 전력점 추적(MPPT, Maximum Power Point Tracking) 알고리즘이 필요하다[1][2].
일반적으로 많이 사용하는 MPPT 알고리즘은 P&O(Perturbation and Observation), InC(InCremental Conductance) 그리고 Fuzzy 등이 있다[3]-[8]. P&O와 InC 알고리즘은 고정된 전압 변화 폭이 클 경우 MPP 주변에서의 큰 진동 때문에 정상상태에서 오차가 크게 발생하고, 스텝 크기의 값이 작을 경우에는 부하 또는 일사량이 변화되면 동적 응답이 늦어지는 단점이 있다. Fuzzy는 적은 오버슈트로 MPP를 보다 신속하게 추적할 수 있으며, MPP를 찾은 후 진동을 최소화 할 수 있다.
인공지능(Artificial intelligence)은 컴퓨터가 인간의 지능적인 행동을 모방할 수 있도록 하는 기계학습의 핵심 분야로서, 최근 인공 신경망(Artificial neural network)에 대한 연구가 활발히 진행되고 있다. 인공 신경망은 인간의 생물학적 신경망 동작을 흉내 낼 수 있는 인공망으로 비선형 시스템에서 입력과 출력사이의 복잡한 관계를 모델링하는 데 널리 사용된다[9].
본 연구는 기존의 알고리즘보다 신속하게 MPP를 추적할 수 있는 모델을 구현하였다. 제안 모델은 인공 신경망의 학습 데이터를 위해 다양한 일사량과 온도의 조합에 대해서 기존 MPPT 알고리즘으로 MPP의 전류와 전압을 찾았다. 획득한 MPP 데이터는 입력 노드를 일사량과 온도로 그리고 출력 노드를 전류와 전압으로 하여 학습하였다. 최종적으로 학습된 값을 PV(Photovoltaic)의 전류-전압과 연결하여 보다 신속하게 MPP 추적하는 모델을 구현하였다. 인공 신경망은 매트랩(Matlab)에서 제공하는 Nftool을 사용하였으며, 실험은 영암 F1 경기장 1 전기실의 실제 일사량 및 온도 데이터를 사용하였다.
본 논문은 2장에서 관련연구로서 P&O, InC 등 기존 MPPT 알고리즘에 대해서 서술하였으며, 3장에서 MPPT 모델을 제안하였다. 또한, 4장에서 구현된 모델의 실험 결과 및 비교 분석을 하였으며, 마지막으로 결론에 대해서 서술하였다.
Ⅱ. 관련 연구
2.1 MPPT 알고리즘
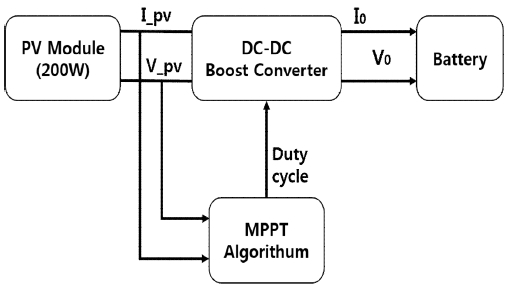
PV는 온도와 일사량에 따라 단락 전류와 개방 전압의 특성이 변화하게 되며, PV의 전력 활용의 효율을 극대화 할 수 있는 MPP의 위치도 온도와 일사량에 따라 변하게 된다. MPPT 알고리즘은 온도와 일사량에서 생산할 수 있는 MPP를 달성하기 위해 태양전지와 부하 사이에 삽입된 DC-DC 컨버터를 제어하는 알고리즘이다. 그림 1에 태양광 발전 시스템의 구성도에 대해서 나타냈다.
태양광 발전 시스템은 태양에너지를 전기에너지로 변환하는 PV 모듈과 필요한 전압으로 변환하거나, 안정화하기 위한 DC-DC 컨버터 그리고 컨버터를 제어하기 위한 MPPT 알고리즘으로 구성된다. 표 1에 본 논문에서 사용한 Kyocera KC200GT 패널 사양에 대해서 나타냈다.
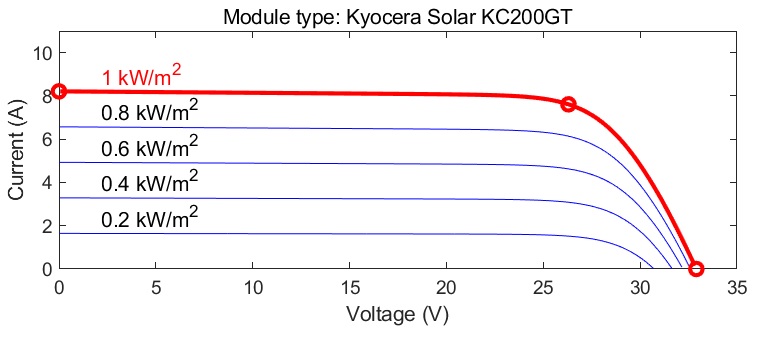
또한, 그림 2에 본 논문에서 사용한 PV의 온도에 대한 전류-전압 특성에 대해서 나타냈으며, 그림 3에 일사량에 대한 전류-전압 특성에 대해서 나타냈다. 그림 2와 3에서 알 수 있듯이 PV는 온도가 상승할수록 낮은 전압으로 MPP를 가지며, 온도가 하강될수록 높은 전압으로 MPP를 가진다. 또한 일사량이 상승하면 높은 전류로 MPP를 가지며, 일사량이 하강하면 낮은 전류로 MPP를 가진다. 그림 4에 DC-DC 컨버터에 대해서 나타냈다.
부스트 컨버터는 인덕터, 다이오드, 캐퍼시터, 스위칭 부분으로 이루어져 있다. 먼저 스위치를 ON 하면 인덕터와 스위칭 소자에 전류가 흐르게 되며, 이 때 1/2LI2의 에너지가 인덕터에 저장된다. 또한, 스위치를 OFF 하면 인덕터에 역기전력이 발생하게 되는데, 그 기전력의 방향은 전원의 전압과 같은 방향이 된다. 따라서 전원의 전압과 인덕터에 생성된 전압이 직렬연결이 되어 부하에 가해지게 된다. 스위칭이 되지 않으면 전원의 전압이 그대로 부하측에 가해지게 된다. 캐퍼시터는 리플 전압을 줄이기 위해서 부착한다[10].
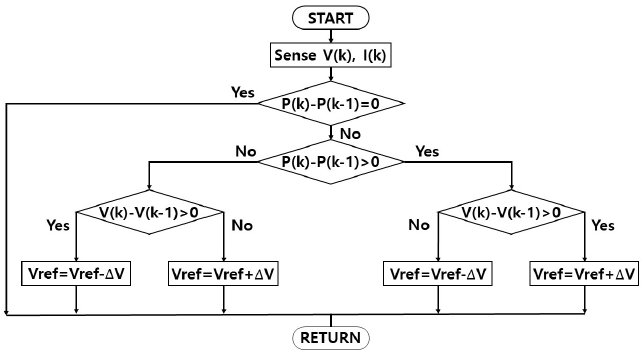
P&O 알고리즘은 PV의 주기적인 증감률과 전류 주기에서 측정되는 전력의 증감률에 의해서 작동하는 방식으로 전압이 한 방향으로 이동하고 그에 따라 전력이 증가하면 그 방향으로 동작점을 이동시키고, 전력이 감소하면 반대방향으로 동작점을 이동시킨다. 즉, 전압의 변화에 따른 방향이 한 번 결정되면 빠른 응답과 정상상태에서의 변동을 고려하여 설정된 일정한 비율로 동작점이 이동하게 된다. 그림 5에 P&O 알고리즘에 대해서 나타냈다[11]-[13].
P(k)는 현재전력을 나타내며 P(k-1)은 과거전력을 나타낸다. V(k)는 현재전압을 나타내고 V(k-1)은 과거전압을 나타낸다. ΔV는 전압차를 나타낸다. P&O 알고리즘은 MPP에 도달하기 위한 매우 우수한 방식으로 태양전지의 특성에 독립적이며, 단점은 정상상태에서의 출력 전력의 미소 진동이 존재하며 출력전력의 손실이 있다[13].
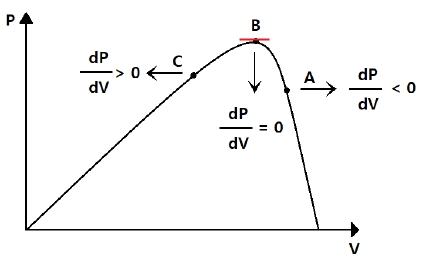
InC 알고리즘은 PV의 V-P 출력곡선의 기울기를 이용하는 방식으로 그 특성이 안정적이고 구현방법이 간단하다. 또한, P&O 방식과 함께 현장에서 가장 많이 사용되고 있는 방법 중 하나이며 MPP에서 V-P 특성곡선의 기울기가 0라는 것을 이용하여 기울기의 크기와 부호에 따라 MPP를 찾는 방식이다. 그림 6에 InC 제어원리에 대해서 나타냈다[12]-[14].
| (1) |
| (2) |
| (3) |
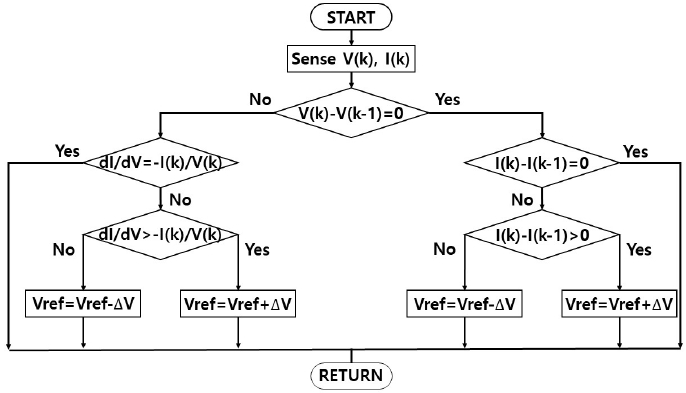
식 (1)은 V-P 특성곡선의 기울기가 양수로서 MPP의 좌측 지점이고, 식 (2)는 음수로써 MPP의 우측지점을 나타내며, 식 (3)은 기울기가 0으로 MPP 지점이다. InC는 P&O의 단점을 보완하기 위한 알고리즘으로 태양전지의 출력전압이 항상 MPP 전압에 추종하도록 해서 MPP 추적제어에 벗어나지 않는 장점이 있다. 그러나 많은 연산이 필요하고, 급격한 일사량의 변화에 대해서 MPPT를 실패할 확률이 높다. 그림 7에 InC 알고리즘에 대해서 나타냈다[15][16].
V(k)는 현재전압을 나타내고 V(k-1)은 이전전압을 나타낸다. I(k)는 현재 전류를 나타내고 I(k-1)은 이전 전류를 나타낸다. dI와 dV는 각각 PV 전류와 PV 전압의 변화량이다. ΔV는 전압차를 나타낸다. 그림 8에 Fuzzy, P&O, InC 알고리즘을 이용하여 MPP를 추적하는 실험결과에 대해서 나타냈다.
실험은 0.1t 동안 일사량은 691.5W/m², 온도는 38.9℃로 설정하여 세 가지 알고리즘으로 MPP를 추적하게 하였다. P&O 알고리즘과 InC 알고리즘에 비해 Fuzzy 알고리즘이 0.03t ~ 0.04t가량 더 빨리 MPP를 찾고 안정적인 전력을 출력하는 것을 확인하였다. 이를 바탕으로 Fuzzy 알고리즘으로 MPP를 추적하는 실험에서 얻은 온도, 일사량, MPP 데이터를 학습에 이용하였다.
Ⅲ. 제안 MPPT 모델
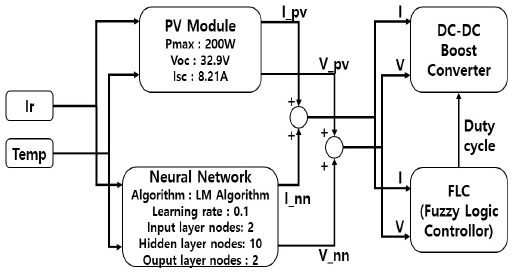
제안 모델은 다양한 일사량과 온도의 조합에 대해서 기존 MPPT 알고리즘으로 MPP를 찾았다. 또한, MPP 데이터를 인공 신경망을 이용하여 일사량과 온도에 대한 전류-전압을 학습하였다. 최종적으로 학습된 값을 PV의 전류-전압과 연결하여 일사량 및 온도 변화에 따라 기존 MPPT 알고리즘들보다 신속히 MPP를 추적하는 모델을 구현하였다. 그림 9에 제안모델에 대해 나타냈다.
제안 모델은 PV, 신경회로망, MPPT 알고리즘인 FLC, DC–DC 컨버터로 구성된다. 본 연구에서는 인공 신경망으로 학습하기 위하여 Fuzzy 알고리즘이 기존 P&O와 InC 알고리즘 보다 추적시간이 우수하다는 결과를 바탕으로 FLC(Fuzzy Logic Controller)를 이용하여 다양한 일사량과 온도의 조합에 대해서 MPP를 찾아 인공 신경망의 학습 데이터로 사용하였다.
일사량과 온도에 따른 PV의 전류-전압인 I_pv와 V_pv는 FLC에 입력되며, 연산 규칙에 의해 출력된 듀티 사이클(Duty cycle)의 변화로 DC-DC 컨버터를 제어하여 MPP점을 찾는다.
그림 10에 PV와 인공 신경망 모듈에 대해 나타냈다. PV 모듈에서는 광전류를 제어하는 IL Ctrl을 통해 온도와 일사량이 입력으로 들어간다. 또한, 직렬 저항 Rs와 병렬저항은 PV의 전압 손실과 누출 전류를 나타내며, I_pv와 V_pv 를 출력한다.
그림 11은 Fuzzy 제어 회로 모듈에 대해 나타냈다. 그림 11의 1과 2는 각각 전압과 전류로써 Filter를 통해 Vn과 In으로 나타난다. 전압과 전류가 곱해져 Pn과 Pb로 나타나고 발전량의 차이와 전압의 차이로 Pn-Pb, Vn-Vb로 나타난다. 각 값들이 FLC의 Input으로 들어가며 표 2의 멤버쉽 값으로 구성된다. Output값으로 표 3의 전압 듀티 사이클이 스위칭 되며 제어된다.
표 2에 멤버쉽 함수에 대해서 나타냈다. 전압과 전력의 변량을 환산하기 위해, PB(Positive Big), PM(Positive Medium), PS(Positive Small), NS(Negative Small), ZE(Zero), NM(Negative Medium), NB(Negative Big) 등 7개의 퍼지 변수로 설계된다. 또한 표 3에 멤버쉽 입출력 값에 대해 나타냈다.
FLC의 입력은 이전 전압-전력과 현재 전압-전력 과의 차이이다. 예를 들어 이전 전압이 10V이고 현재 전압이 12V이면 차이는 2V로 멤버쉽 함수 PS에 해당한다. 이전 전력량이 500W이고 현재 전력량이 505W이면 차이는 5W/m²로 멤버쉽 함수 PB에 해당한다. FLC의 출력은 듀티 사이클이며, DC-DC 컨버터의 스위치를 제어하여 MPP를 추적한다.
인공 신경망의 입력 노드는 온도와 일사량이며, 출력 노드는 MPP의 전류-전압이다. 이때 PV 온도 범위는 0℃–50℃으로 5℃도 간격으로 변화를 주었으며, 일사량 범위는 200W/m²–1200W/m²으로 200W/m² 간격이다. 총 데이터는 50개의 데이터로서. 학습 데이터는 39개이며, 검증 데이터는 3개이고 테스트 데이터는 8개를 사용하였다.
입력 데이터로 사용할 온도와 일사량의 범위가 다르기 때문에, 데이터의 범위를 일치시키거나 분포를 유사하게 만들어야 한다. 또한, 인공지능은 입출력 데이터의 크기가 작아야 학습이 효과적이기 때문에, 독립변수인 온도와 일사량 데이터를 식 (4)와 같이 min-max 정규화를 사용하여 정규화 하였다.
| (4) |
di는 각 온도와 일사량 데이터이며, min(1:d)은 각 요소 중 가장 작은 값 그리고 max(1:d)은 각 요소 중 가장 큰 값을 나타낸다.
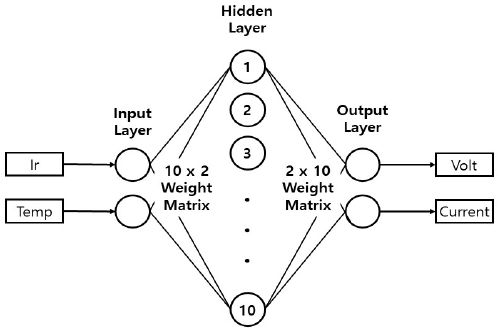
Nftool은 신경망 피팅 도구로 인공 신경망의 입력요소, 출력요소 그리고 중간층 노드 수를 지정하고, LM(Levenberg Marquardt), Bayesian Regularization 그리고 Scaled Confugate Gradient 등의 알고리즘을 선택하면 학습, 검증 그리고 테스트를 진행해주는 툴이다. 본 논문은 Nftool을 이용하여 입력 노드는 2개, 중간층의 노드는 10개, 중간층의 수는 1개, 출력 노드는 2개인 인공 신경망을 구성하였다. 또한, epoch 횟수는 1000회, 학습률은 0.1로 설정하였으며 학습 알고리즘은 오차함수를 테일러 급수로 전개하고 2차 미분을 통하여 근사 최소점을 찾는 LM 알고리즘을 이용하였다. Nftool에서 LM 알고리즘의 설정 가능한 파라미터인 감쇠지수 μ의 초기값은 0.001으로 μ값 감소인자는 0.1로, μ값 증가인자는 10으로 설정하였다. 그림 12에 인공 신경망 구조에 대해서 나타냈다.
표 4에 하이퍼파라메터 변화에 따른 신경망의 오차와 회귀값을 나타냈다.
표에서 볼 수 있듯이, 중간노드수가 10개이고 학습률이 0.1일 경우 회귀 값이 가장 좋았다. 표 5에 본 연구에서 사용된 인공신경망 파라메터에 대해서 나타냈다.
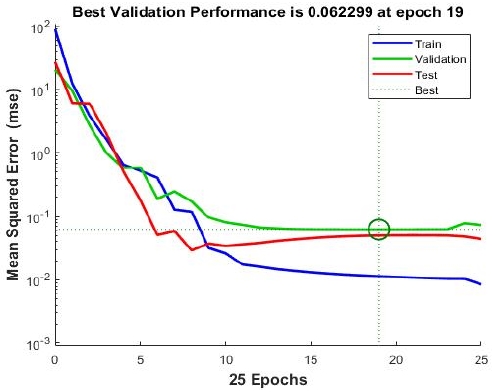
그림 13에 학습 손실값에 대해서 나타냈다. 학습은 검증오차가 6회 반복동안 검증이 중지 될 때까지 진행하였다. 최종 평균 제곱 오차가 작으며, 테스트 세트 오차와 검증 세트 오차의 특성이 유사하다. 또한 19번째 반복에서 최상의 검증 성능이 발생하였으며 과적합이 발생하지 않았다.
그림 14에 학습회귀에 대해서 나타냈다. 회귀 플롯은 훈련, 검증 및 테스트 세트의 목표값에 대한 네트워크 출력 값을 표시한다. 완벽한 Fitting이 되었다고 할 때는 45도 직선에 있어야 하고 이 직선에 있는 네트워크 출력값은 목표값과 같다. 예측값과 실제값 사이에 차이가 발생한다면 오차가 생겨 R값이 작아진다. 따라서 보다 정확한 결과가 필요할 경우 Nftool에서 Retrain을 클릭하여 네트워크를 재교육 할 수 있다. 이후 네트워크의 초기 가중치와 편향이 변경되어 재교육 후 개선된 네트워크를 생성 할 수 있다. 본 실험에서는 신경망의 예측 정확도를 인공 신경망에 학습시킨 50개의 시뮬레이션 및 회귀분석 결과 R값이 0.99이상으로 상당히 우수한 상관계수를 확인할 수 있다[17][18].
이와 같이 인공 신경망으로 학습된 전류-전압은 PV에서 출력된 전류-전압 값과 합하여 기존 MPPT 알고리즘의 입력으로 사용된다. 이때 IL Ctrl을 통과한 전류 전압과 학습된 전류-전압을 조정하여 최대의 발전량을 보이는 실험을 진행하였다. PV는 정격 전류-전압이 있기 때문에 임의로 흘려주게 되면 모듈이 고장 나 제대로 측정되지 않는 경우가 발생한다. 따라서 가장 높은 발전량을 보이고 오류가 발생하지 않는 범위 내에서 실험을 진행하였다.
Ⅳ. 결과 및 비교 분석
실험은 매트랩 2019a 버전을 이용하여 구성하였고, 일사량과 온도를 변화시켜주었으며 입력데이터는 Simulink의 Signal Builder를 사용하였다.
표 6에서 실제 실험 데이터는 음영으로 표시하였다. 사용 데이터는 공공데이터 포털에서 제공하는 한국서부발전 태양광 발전 데이터 중 경사 일사량이 평균적으로 가장 높은 영암 F1 경기장 1 전기실을 실험 데이터로 사용하였다. 또한, 가장 경사일사량이 높았던 2016년 8월 19일 데이터를 사용하였다.
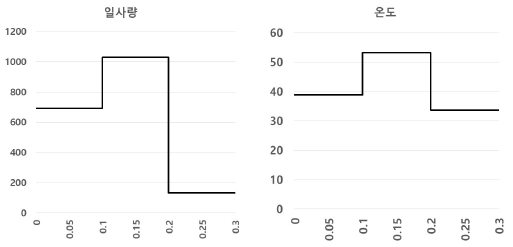
각 구간별 일사량과 온도 실험데이터를 그림 15에 나타냈다.
0t ~ 0.1t : 691.5W/m², 38.9℃
0.1t ~ 0.2t : 1029.8W/m², 53.2℃
0.2t ~ 0.3t : 131.6W/m², 33.7℃
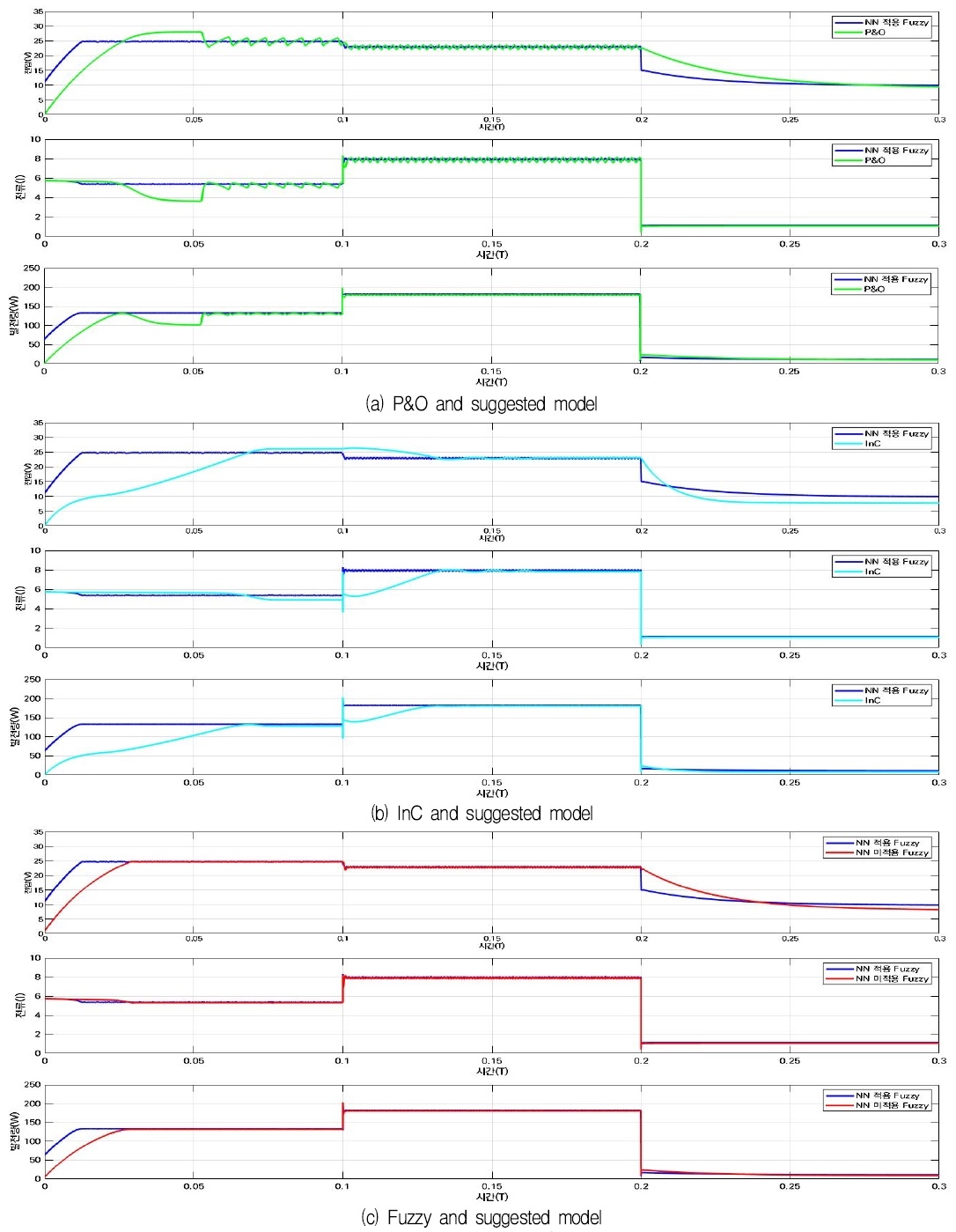
표 7과 그림 16에 실험 결과에 대해서 나타냈다. P&O 알고리즘은 0t ~ 0.1t 구간에서 0.025t에 MPP를 찾지만 전압과 전류의 불안정으로 인해 전압을 높이다가 낮추고, 반면 전류는 낮아지다가 높아지는 모습을 보이며 MPP를 찾지 못하지만 다시 조절을 통해 0.055t에서 MPP를 찾는 모습을 보인다. 또한, 0.1t ~ 0.2t 구간에서 0.103t에 MPP를 찾으며, 0.2t ~ 0.3t 구간에서 0.27t에서 MPP를 찾는다.
InC 알고리즘은 0t ~ 0.1t 구간에서 0.07t에 MPP점을 찾으며, 0.1t ~ 0.2t 구간에서 0.14t에 MPP를 찾는다. 또한, 0.2t ~ 0.3t 구간에서 0.28t에서 MPP를 찾는다. Fuzzy 알고리즘은 0t ~ 0.1t 구간에서 0.027t에 MPP를 찾으며, 0.1t ~ 0.2t 구간에서 0.1t에 전류가 불안정한 모습을 보이며 MPP점을 다소 늦게 찾는 모습을 보였으나 0.1006t에서 MPP를 찾는다. 또한, 0.2t ~ 0.3t 구간에서 천천히 전압을 낮추며 0.28t에서 MPP를 찾는다. 제안 모델은 0t ~ 0.1t 구간에서 0.015t에 MPP를 찾으며, 0.1t ~ 0.2t 구간에서 0.1001t에서 MPP를 찾는다. 또한, 0.2t ~ 0.3t 구간에서 0.21t에서 MPP를 찾는다. 실험결과 일사량과 온도 변화가 있는 0t ~ 0.3t 구간에서 MPP 추적시간은 기존 알고리즘인 P&O와 InC 그리고 Fuzzy는 0.428t, 0.49t, 0.4076t이였으며, 제안 모델은 0.32511t로서 기존 알고리즘 보다 0.1t 이상 신속하게 MPP를 추적하였다.
본 연구에서 신경망 학습을 위해 사용한 데이터는 총 50개의 데이터로 영암 F1 경기장의 데이터를 사용하였다. 그러나 실제로 다른 지역에 제안 모델을 적용할 시 보다 정교한 학습 결과를 적용하기 위해서는 다양한 기상요소 및 환경조건 그리고 계절 등 많은 데이터가 필요하며, 이러한 학습을 위한 데이터 수집과 학습을 통한 추가 비용이 발생할 수 있다.
Ⅴ. 결 론
본 연구는 인공 신경망을 이용하여 일사량과 온도에 대한 최적의 MPP 전류 및 전압 값을 학습하여, 학습된 결과를 PV의 전류 및 전압과 연결하여 급격한 일사량 및 온도 변화에 따라 기존 MPPT 알고리즘들 보다 신속한 MPP 추적하는 모델을 제시하였다. 실험결과 0~0.1t 구간에서 기존 알고리즘들은 0V에서 시작하는 반면 제안모델은 10V에서 시작하여 동일한 MPP점을 훨씬 더 빨리 찾는다는 것을 확인 할 수 있다. 또한, 0.2t ~ 0.3t구간에서도 가존 알고리즘들은 전압을 서서히 감소시키며 MPP점을 찾아가는 반면 제안 모델은 해당 구간에서 학습된 데이터를 바탕으로 MPP점을 더욱 빨리 추적하는 것을 확인할 수 있다. 본 논문에서 제시한 MPPT 모델은 기존 알고리즘에 보다 MPPT 속도 및 정상상태 오차에서 모두 양호한 응답특성을 나타냈다.
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다.(No. 20194030202290)
References
- J. K. Min and W. S. Choi, "Analysis of Power Generation Characteristics according to the MPPT Algorithm Period", The Transactions of the Korean Institute of Electrical Engineers, Vol. 67, No. 4, pp. 233-237, Dec. 2018.
- S. K. Ock and O. Yang, "A Study on the New MPPT Control Method for Grid-connected PV Generation System", The Journal of Korean Institute of Information Technology, Vol. 10, No. 2, pp. 28-3, Feb. 2012.
- S. H. Moon, J. W. Kim, B. G. Park, and J. M. Kim, "Maximum Power Control of Tidal Current Generation System using P&O Algorithm", The Transactions of the Korean Institute of Power Electronics, Vol. 22, No. 3, pp. 199-206, Jun. 2017.
- C. I. William and R. Ramesh, "Comparative study of P&O and InC MPPT algorithms", American Journal of Engineering Research, Vol. 2, No. 12, pp. 402-408, Dec. 2013.
-
R. Algarín, Carlos, J. T. Giraldo, and O. R. Alvarez, "Fuzzy logic based MPPT controller for a PV system", Energies. Vol. 10, No. 12, pp. 2036-2043, Dec. 2017.
[https://doi.org/10.3390/en10122036]

-
C. Larbes, S. M. Ait-Cheikh, T. Obeidi, and A. Zerguerras, "Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system", Renewable Energy, Vol. 34, No. 10, pp. 2093-2100, Oct. 2009.
[https://doi.org/10.1016/j.renene.2009.01.006]

-
Yilmaz Unal, Kircay Ali, and Borekci Selim, "PV System fuzzy logic MPPT method and PI control as a charge controller", Renewable and Sustainable Energy Reviews, Vol. 81, Part 1, pp. 994-1001, Jan. 2018.
[https://doi.org/10.1016/j.rser.2017.08.048]

-
B. Bendib, F. Krim, H. Belmili, M. F. Almi, and S. Boulouma, "Advanced Fuzzy MPPT Controller for a stand-alone PV system", Energy Procedia, Vol. 50 pp. 383-392, 2014.
[https://doi.org/10.1016/j.egypro.2014.06.046]

- Jobeda J. Khanam and Simon Y. Foo, "Modeling of a photovoltaic array in MATLAB simulink and maximum power point tracking using neural network", Journal of Electrical & Electronic Systems, Vol. 2, No. 2, pp. 40-46, Jul. 2018.
-
D. H. Yoo, G and Y. Jeong, "Novel Ozone Generation Power Supply using a Topology of the PFC DC-DC Boost Converter and Single-phase Half-bridge Inverter", The Journal of Korean Institute of Information Technology, Vol. 11, No. 7, pp. 19-30, Jul. 2013.
[https://doi.org/10.14801/kiitr.2013.11.7.19]

- B. S. Kim, J. J. King, W. S. Sim, J. M. JO, and H. C., "A study on High-Efficiency MPPT Algorithm Based on P&O Method with Variable Step Size", The Transactions of the Korean Institute of Power Electronics, Vol. 24, No. 1, pp. 1-8, Feb. 2019.
-
N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, "Optimization of perturb and observe maximum power point tracking method", IEEE Trans. on Power Electronics, Vol. 20, No. 4, pp. 963-973, Jul. 2005.
[https://doi.org/10.1109/TPEL.2005.850975]

- Y. S. Choi, E. G. Kim, and J. W. Jung, "MPPT Control Technique for Photovoltaic System", KIPE MAGAZINE, Vol. 18, No. 1, pp. 29-36, Feb. 2013.
-
J. H. Shim, S. D. Yang, S. H. Jung, J. Y. Choi, I. Choy, J. U. An, and D. H. Lee, "Analysis of various MPPT algorithms for PCS", Journal of the Korean Solar Energy Society, Vol. 31, No. 2, pp. 16-21, Apr. 2011.
[https://doi.org/10.7836/kses.2011.31.2.016]

- S. R. Chafle and U. B. Vaidya, "InCremental Conductance MPPT Technique FOR PV System", International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, Vol. 2, No. 6, pp. 2719-2726, Jun. 2013.
-
F. Liu, S. Duan, F. Liu, B. Liu, and Y. Kang, "A variable step size InC MPPT method for PV systems", IEEE Transactions on industrial electronics, Vol. 55, No. 7, pp. 2622-2628, Jul. 2008.
[https://doi.org/10.1109/TIE.2008.920550]

-
Ankit Chaturvedi, "Rainfall Prediction using Back-Propagation Feed Forward Network", International Journal of Computer Applications, Vol. 119, No. 4, pp. 1-5, Jun. 2015.
[https://doi.org/10.5120/21052-3693]

- Bitna Kim and Young Ho Park, "Beginner’s Guide To Neural Networks For The Mnist Dataset Using Matlab", Korean J. Math, Vol. 26, No. 2, pp. 337-348, Jun. 2018.

2016년 2월 : 청주대학교 전자공학과(공학사)
2018년 9월 ~ 현재 : 가천대학교 IT융합공학과(석사 과정)
관심분야 : 딥러닝, 빅 데이터, AI, 로봇제어, 안드로이드

2016년 3월 ~ 현재 : 가천대학교 IT대학 에너지 IT학과 재학
관심분야 : 딥러닝, 빅 데이터, AI, 사물인터넷

1986년 2월 : 단국대학교 전자공학과(공학사)
1989년 2월 : 단국대학교 전자공학과(공학석사)
2009년 2월 : 인천대학교 컴퓨터공학과(공학박사)
1994년 ~ 현재 : 가천대학교 IT대학 에너지 IT학과 교수
관심분야 : 데이터 마이닝, 딥러닝, 강화학습, 사물인터넷